Перекрепление стойки двухпролетной одноэтажной рамы под действующей постоянной нагрузкой

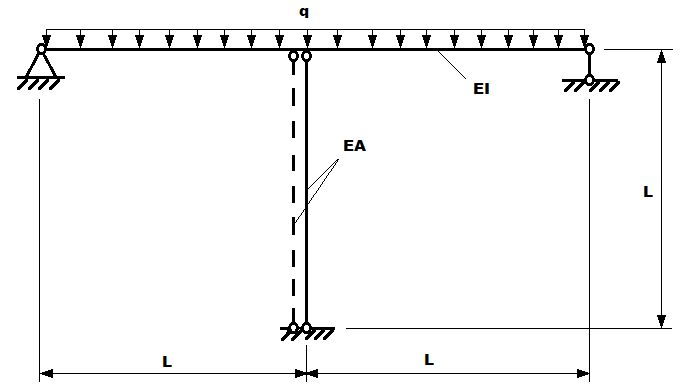
Цель: Определение внутренних усилий в элементах двухпролетной одноэтажной рамы до и после перекрепления стойки под действующей постоянной нагрузкой.

Имя файла с исходными данными: Rearrange_Frame.MPR

Формулировка задачи: Двухпролетный ригель рамы, шарнирно опертый по торцам и имеющий среднюю опору в виде качающейся стойки, находится под действием постоянной равномерно распределенной нагрузки. В ходе реконструкции производится замена стойки на равную по жесткости в следующей последовательности: устанавливается заменяющая стойка и затем демонтируется исходная стойка.  Определить максимальные изгибающие моменты в ригеле рамы M_I, M_II и продольные силы в стойках N_I, N_II до и после перекрепления.

Исходные данные:

EF = 2.0·107 т	- продольная жесткость поперечного сечения ригеля и стоек;
EI = 1.2·108 т·м2	- изгибная жесткость поперечного сечения ригеля и стоек;
L = 6.0 м	- длина пролетов ригеля и высота стоек;
q = 4.0 т/м	- равномерно распределенная постоянная вертикальная нагрузка на пролеты ригеля.

 

Конечноэлементная модель: Расчетная  схема – плоская рама, элементы ригеля – 24 стержневых элемента типа 2, элементы стоек – 24 стержневых элемента типа 2. Сетка конечных элементов разбита по продольным осям конструктивных элементов с шагом 0.5 м. Узел левого торца ригеля закреплен по направлениям степеней свободы X, Z. Узлы нижних торцов стоек закреплены по направлениям степеней свободы X, Z. Элементы верхних торцов стоек имеют шарнир по направлению степени свободы UY. Количество узлов в расчетной схеме – 37. На первой стадии монтажа присутствуют элементы ригеля 1 – 24 и исходной стойки 25 – 36. На второй стадии монтажа присутствуют элементы ригеля 1 – 24 и заменяющей стойки 37 – 48. На обеих стадия действует накапливаемое загружение q.

Результаты решения в SCAD

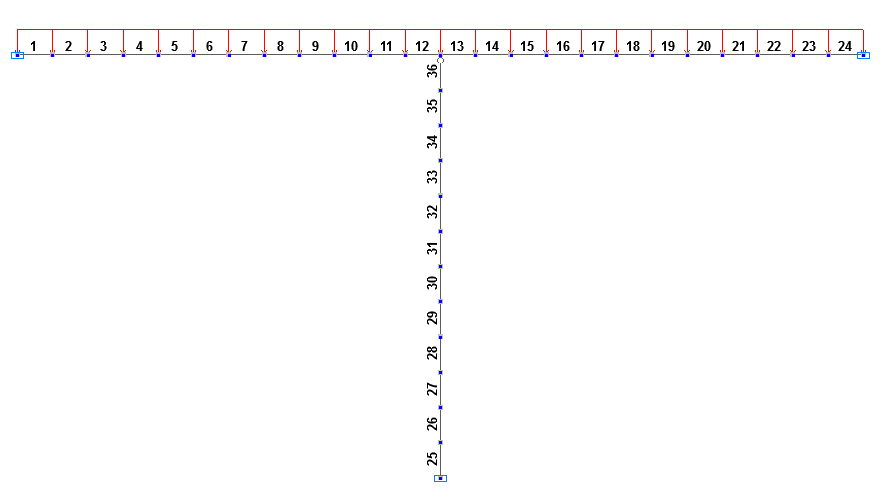
Расчетные схемы на первой и второй стадиях монтажа

 

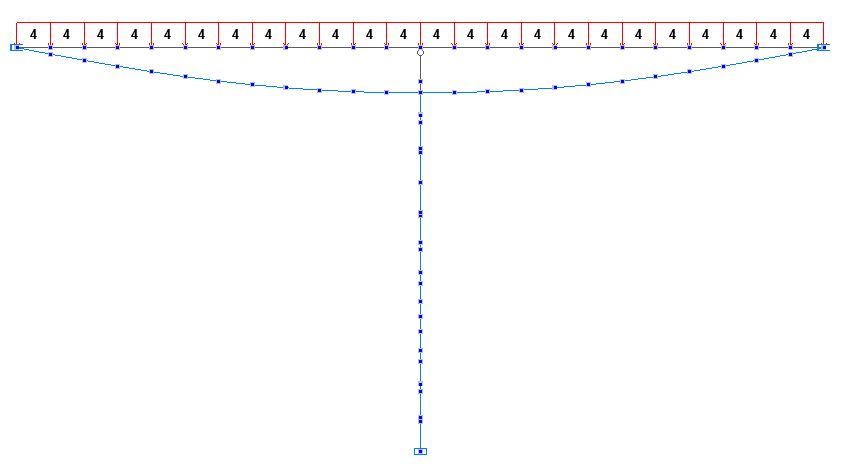
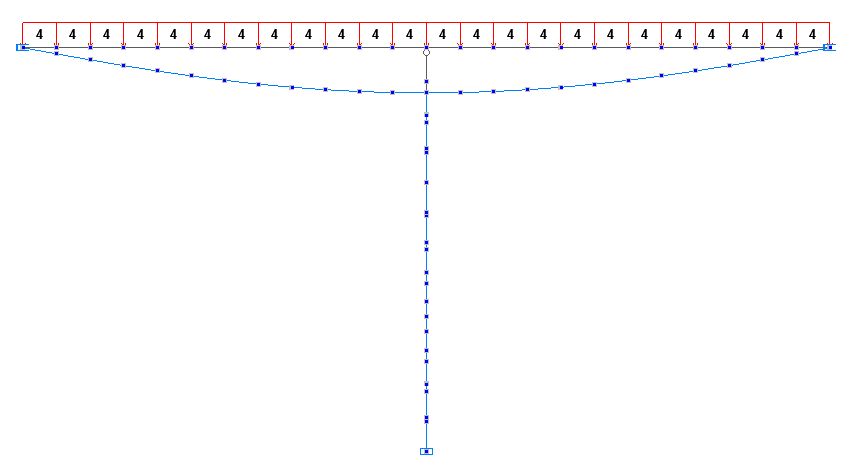
Деформированные схемы на первой и второй стадиях монтажа

 

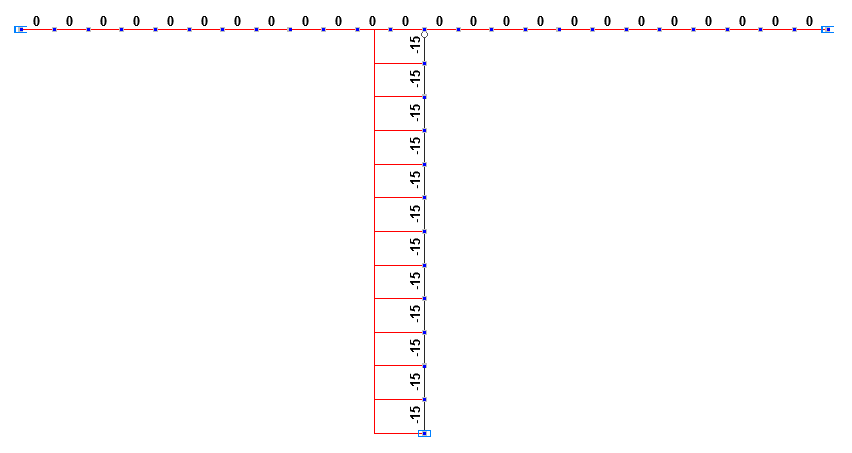
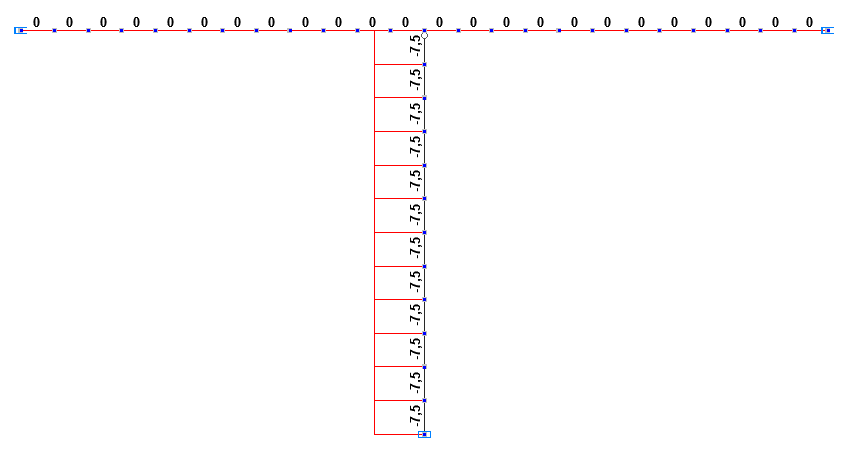
Эпюры продольных сил N_I, N_II на первой и второй стадиях монтажа (т)

 

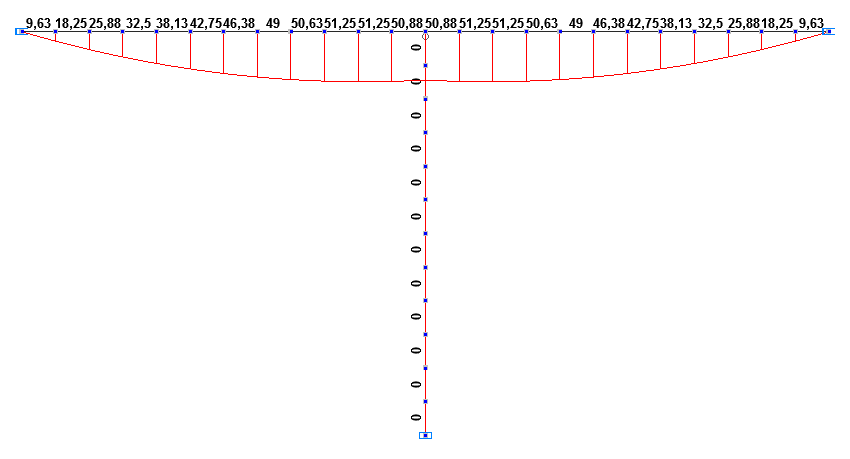
Эпюры изгибающих моментов M_I, M_II на первой и второй стадиях монтажа (т∙м)

 

Сравнение решений:

 

Параметр	Теория	SCAD	Отклонения, %
Максимальный изгибающий момент в ригеле рамы на первой стадии монтажа MI, т∙м	34.03	34.03	0.00
Продольная сила в стойке рамы на первой стадии монтажа NI, т	-15.0	-15.0	0.00
Максимальный изгибающий момент в ригеле рамы на второй стадии монтажа MII, т∙м	51.26	51.25	0.02
Продольная сила в стойке рамы на второй стадии монтажа NII, т	-7.5	-7.5	0.00

Замечания: При аналитическом решении максимальные изгибающие моменты в ригеле рамы M_I, M_II и продольные силы в стойках N_I, N_II до и после перекрепления определяются по следующим формулам:

\[ M_{I} =\frac{1}{2}\,\cdot \,q\,\cdot \,L^{2}-\frac{1}{2}\cdot \,q\,\cdot L\,\cdot \,\frac{\frac{5}{24}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{3}}{6\,\cdot \,EI}+\frac{L}{EA}}+\frac{1}{8}\,\cdot \,q\,\cdot \,\left( {\frac{\frac{5}{24}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{3}}{6\,\cdot \,EI}+\frac{L}{EA}}} \right)^{2} \] \[ N_{I} =-q\,\cdot \,\frac{\frac{5}{24}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{3}}{6\,\cdot \,EI}+\frac{L}{EA}} \] \[ M_{II} =\frac{441}{512}\,\cdot \,q\,\cdot \,L^{2}-\frac{21}{16}\,\cdot \,q\,\cdot \,L\,\cdot \,\frac{\frac{15}{96}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{2}}{6\,\cdot \,EI}+\frac{L}{EA}}+\frac{1}{2}\,\cdot \,q\,\cdot \,\left( {\frac{\frac{15}{96}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{2}}{6\,\cdot \,EI}+\frac{L}{EA}}} \right)^{2} \] \[ N_{II} =-\,q\,\cdot \,\frac{\frac{5}{48}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{2}}{6\,\cdot \,EI}+\frac{L}{EA}} \]