Последовательный монтаж сталежелезобетонной однопролетной балки

Цель: Определение прогибов сталежелезобетонной однопролетной балки по стадиям монтажа.

Формулировка задачи: Монтаж сталежелезобетонной однопролетной балки осуществляется в следующей последовательности:

На первой стадии монтажа устанавливается на опоры стальная двутавровая балка, на подпорках от нижнего пояса балки устраивается опалубка под железобетонную плиту, на опалубке устанавливается арматурный каркас и укладывается монолитный бетон. На этой стадии на стальную балку действуют нагрузки от собственного веса q₁₁ и от веса свежеуложенного бетона q₁₂.
На второй стадии монтажа разбирается опалубка, и железобетонная плита начинает изгибаться поперек стальной балки под собственным весом.
На третьей стадии монтажа к сталежелезобетонной балке прикладываются эксплуатационные нагрузки от веса конструкции покрытия по железобетонной плите q₂ и транспортная нагрузка P₂.

Определить максимальные прогибы сталежелезобетонной балки на первой w₁ и третьей w₂ стадиях монтажа.

Имя файла с исходными данными: Wiring_Girder.MPR

Исходные данные:

E_st = 2.1·10⁶ кгс/см²	- модуль упругости материала стальной балки;
E_b = 3.06·10⁵ кгс/см²	- модуль упругости материала железобетонной плиты;
υ_st = 0.3	- коэффициент Пуассона стали;
υ_b= 0.2	- коэффициент Пуассона железобетона;
L = 1365.0 см	- длина пролета сталежелезобетонной балки;
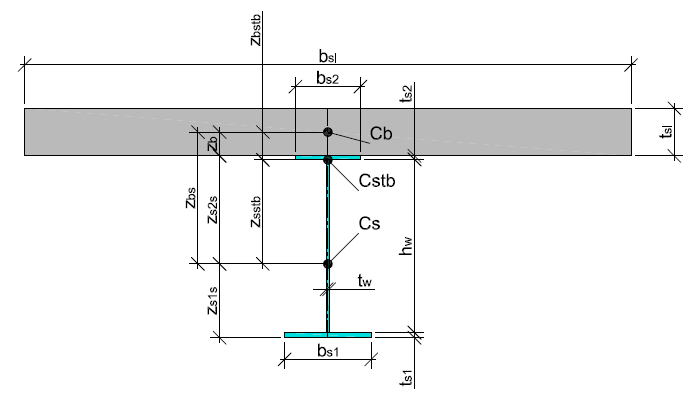
b_s1 = 40.0 см	- ширина нижнего пояса стальной балки;
t_s1 = 2.4 см	- толщина нижнего пояса стальной балки;
b_s2 = 30.0 см	- ширина верхнего пояса стальной балки;
t_s2 = 1.6 см	- толщина верхнего пояса стальной балки;
h_w = 80.0 см	- высота стенки стальной балки;
t_w = 1.2 см	- толщина стенки стальной балки;
b_sl = 280.0 см	- ширина железобетонной плиты;
t_sl = 22.0 см	- толщина железобетонной плиты;
q₁₁ = 0.2072 т/м	- равномерно распределенная по линии вертикальная нагрузка от собственного веса стальной балки;
q₁₂ = 0.6050 т/м²	- равномерно распределенная по площади вертикальная нагрузка от собственного веса железобетонной плиты;
q₂ = 0.3770 т/м²	- равномерно распределенная по площади вертикальная нагрузка от веса конструкции покрытия по железобетонной плите;
P₂ = 39.60 т/м	- равномерно распределенная по линии вертикальная транспортная нагрузка.

Конечноэлементная модель: Расчетная схема – система общего вида, элементы стальной балки – 68 стержневых элементов типа 5, элементы железобетонной плиты – 952 элемента оболочки типа 44, элементы сопряжения стальной балки и железобетонной плиты – 69 элементов типа 100, элементы подпорок опалубки - 1035 элементов типа 100. Сетка конечных элементов стальной балки разбита по продольной оси с шагом 0.2 м. Сетка конечных элементов железобетонной плиты разбита в продольном и поперечном направлениях с шагом 0.2 м. Узел левого торца балки закреплен по направлениям степеней свободы X,Y, Z, UX. Узел правого торца балки закреплен по направлениям степеней свободы Y, Z, UX. Количество узлов в расчетной схеме – 1173. На первой стадии монтажа присутствуют элементы стальной балки, железобетонной плиты с пониженным модулем упругости E_b∙10^-3, элементы сопряжения и элементы подпорок. На второй и третьей стадиях монтажа присутствуют элементы стальной балки, железобетонной плиты с нормальным модулем упругости E_b и элементы сопряжения. На всех стадиях действуют нагрузки q₁₁ и q₁₂ накапливаемого загружения q₁. На третьей стадии монтажа действуют нагрузки q₂ и P₂ независимого загружения q₂.

Результаты решения в SCAD:

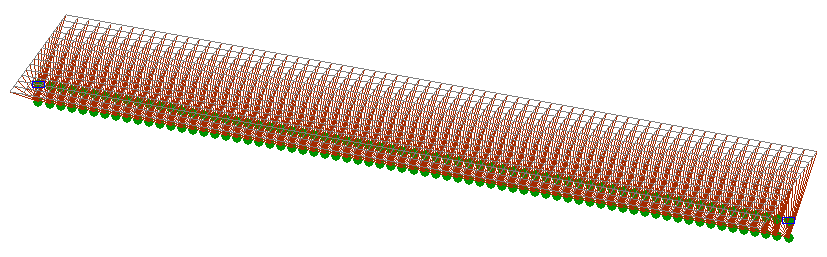
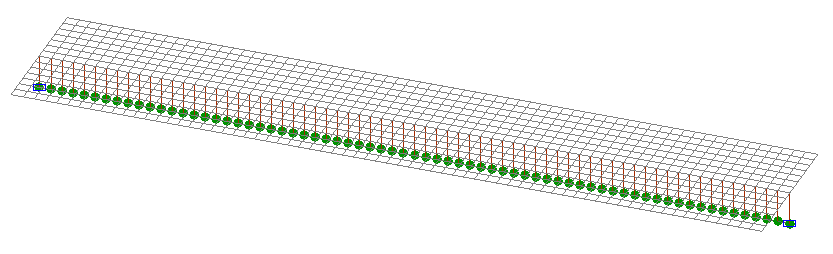
Расчетные схемы на первой и второй, третьей стадиях монтажа

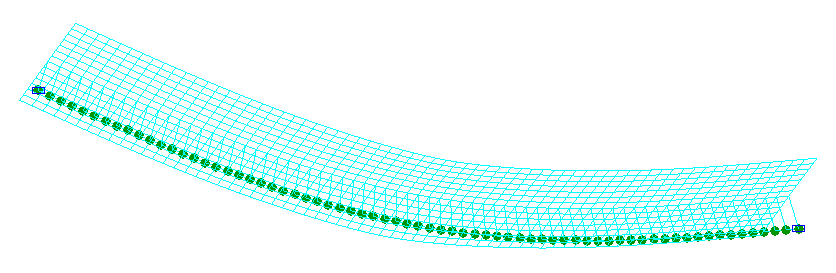
Деформированные схемы на первой и третьей стадиях монтажа

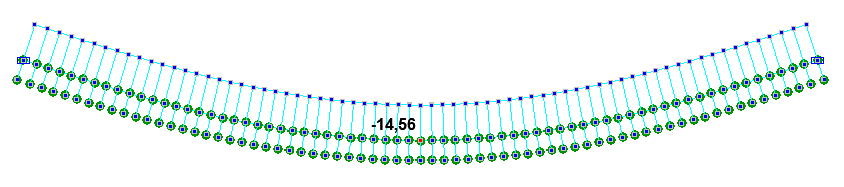
Прогибы на первой w₁ и третьей w₂ стадиях монтажа (мм)

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
Максимальный прогиб сталежелезобетонной балки на первой стадии монтажа w₁, мм	-14.75	-14,56	1.29
Максимальный прогиб сталежелезобетонной балки на третьей стадии монтажа w₂, мм	-44.51	-44,90	0.88

Замечания: При аналитическом решении максимальные прогибы сталежелезобетонной балки на первой w₁ и третьей w₂ стадиях монтажа определяются по следующим формулам:

\[ w_{1} =\frac{5}{384}\cdot \frac{\left( {q_{11} +q_{12} \cdot b_{sl} } \right)\cdot L^{4}}{E_{st} \cdot I_{s} }; \] \[ w_{1} =\frac{5}{384}\cdot \frac{\left( {q_{11} +q_{12} \cdot b_{sl} } \right)\cdot L^{4}}{E_{st} \cdot I_{s} }+\frac{5}{384}\cdot \frac{q_{2} \cdot b_{sl} \cdot L^{4}}{E_{st} \cdot I_{stb} }+\frac{1}{48}\cdot \frac{P_{2} \cdot b_{sl} \cdot L^{3}}{E_{st} \cdot I_{stb} }; \] \[ I_{stb} =I_{s} +A_{s} \cdot z_{sstb}^{2} +\frac{I_{b} }{n_{b} }+\frac{A_{b} }{n_{b} }\cdot z_{bstb}^{2} ;\quad z_{bstb} =z_{bs} -z_{sstb} ;\quad z_{sstb} =\frac{S_{stb} }{A_{stb} }; \] \[ S_{stb} =\frac{A_{b} }{n_{b} }\cdot z_{bs} ;\quad A_{stb} =A_{s} +\frac{A_{b} }{n_{b} };\quad z_{bs} =z_{s2s} +z_{b} ;\quad I_{b} =\frac{b_{sl} \cdot t_{sl} }{12}; \] \[ z_{b} =\frac{S_{b} }{A_{b} };\quad S_{b} =\frac{b_{sl} \cdot t_{sl}^{2} }{2};\quad A_{b} =b_{sl} \cdot t_{sl} ;\quad n_{b} =\frac{E_{st} }{E_{b} }; \] \[ I_{s} =I_{s1s} +I_{ws} +I_{s2s} ;\quad I_{s2s} =I_{s2} +A_{s2} \cdot \left( {t_{s1} +h_{w} +\frac{t_{s2} }{2}-z_{s1s} } \right)^{2}; \] \[ I_{ws} =I_{w} +A_{w} \cdot \left( {t_{s1} +\frac{h_{w} }{2}-z_{s1s} } \right)^{2};\quad I_{s1s} =I_{s1} +A_{s1} \cdot \left( {z_{s1s} -\frac{t_{s1} }{2}} \right)^{2}; \] \[ I_{w} =\frac{t_{w} \cdot h_{w}^{3} }{12};\quad I_{s2} =\frac{b_{s2} \cdot t_{s2}^{3} }{12};\quad I_{s1} =\frac{b_{s1} \cdot t_{s1}^{3} }{12}; \] \[ z_{s2s} =H_{s} -z_{s1s} ;\quad z_{s1s} =\frac{S_{s} }{A_{s} };\quad S_{s} =A_{s1} \cdot \frac{t_{s1} }{2}+A_{w} \cdot \left( {t_{s1} +\frac{h_{w} }{2}} \right)+A_{s2} \cdot \left( {t_{s1} +h_{w} +\frac{t_{s2} }{2}} \right); \] \[ A_{s} =A_{s1} +A_{w} +A_{s2} ;\quad H=H_{s} +t_{sl} ;\quad H_{s} =t_{s1} +h_{w} +t_{s2} ; \] \[ A_{w} =t_{w} \cdot h_{w} ;\quad A_{s2} =b_{s2} \cdot t_{s2} ;\quad A_{s1} =b_{s1} \cdot t_{s1} ; \]