Квадратная панель безбалочного перекрытия, жестко сочлененная с колонной круглого поперечного сечения, под действием поперечной равномерно распределенной нагрузки

Цель:

Определение изгибающих моментов в характерных точках квадратной панели безбалочного перекрытия, жестко сочлененной с колонной круглого поперечного сечения, от воздействия поперечной равномерно распределенной нагрузки.

Файл с исходными данными: Flate_plate_Circular_column.spr

Формулировка задачи:
Квадратная панель безбалочного перекрытия, жестко сочлененная с колонной круглого поперечного сечения, находится под действием поперечной равномерно распределенной нагрузки q. Определить изгибающие моменты M_x, M_y в характерных точках квадратной панели безбалочного перекрытия.

Ссылки:
С. П. Тимошенко, С. Войновский-Кригер, Пластинки и оболочки, Москва, Книжный дом "ЛИБРОКОМ", 2009, стр. 287-289.

Исходные данные:

E = 3.0∙10⁷ Н/м²	- модуль упругости,
ν = 0.2	- коэффициент Пуассона,
h = 0.1 м	- толщина панели безбалочного перекрытия;
a = 2.5 м	- радиус панели безбалочного перекрытия;
c = 0.1∙a = 0.25 м	- радиус поперечного сечения колонны;
q = 100.0 Н/м²	- значение поперечной равномерно распределенной нагрузки.

Конечноэлементная модель:

Расчетная схема – балочный ростверк, плита; элементы панели безбалочного перекрытия – 2412 четырехугольных четырехузловых элементов тонких плит для расчета по теории Кирхгофа-Лява типа 20 и 16 треугольных трехузловых элементов тонких плит для расчета по теории Кирхгофа-Лява типа 15; элемент поперечного сечения колонны – 1 элемент твердого тела типа 100. Сетка конечных элементов панели безбалочного перекрытия разбита в направлениях осей глобальной системы координат с шагом 0.05 м кроме контура опирания, где сетка конечных элементов разбита в радиальном направлении с шагом 0.05 м и в окружном направлении с шагом 11.25°. Направление выдачи усилий – вдоль осей глобальной системы координат. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы UX для кромок панели, расположенных вдоль оси X общей системы координат, и UY для кромок панели, расположенных вдоль оси Y общей системы координат. Мастер-узел твердого тела колонны расположен по центру ее поперечного сечения и закреплен связью по направлению степени свободы Z. Количество узлов в расчетной схеме – 2537.

Результаты решения в SCAD:

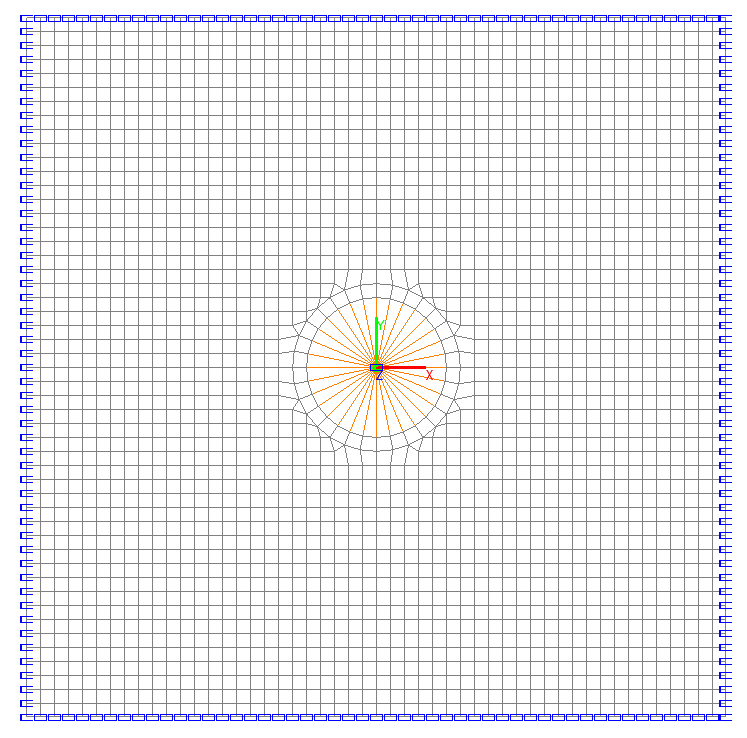
Расчетная схема

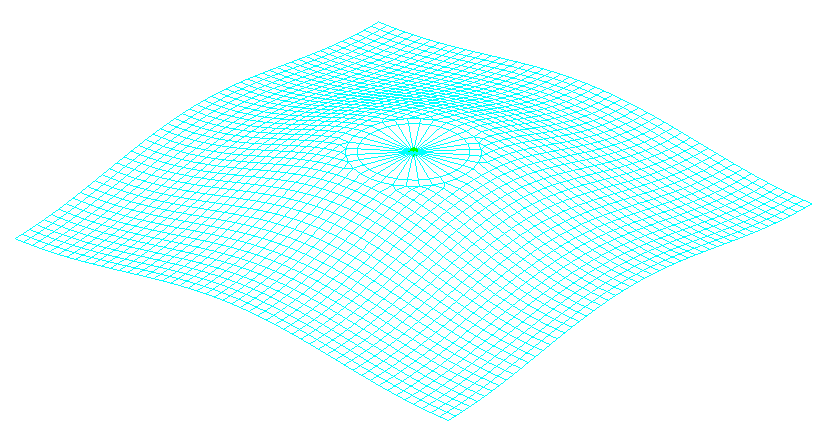
Деформированная схема

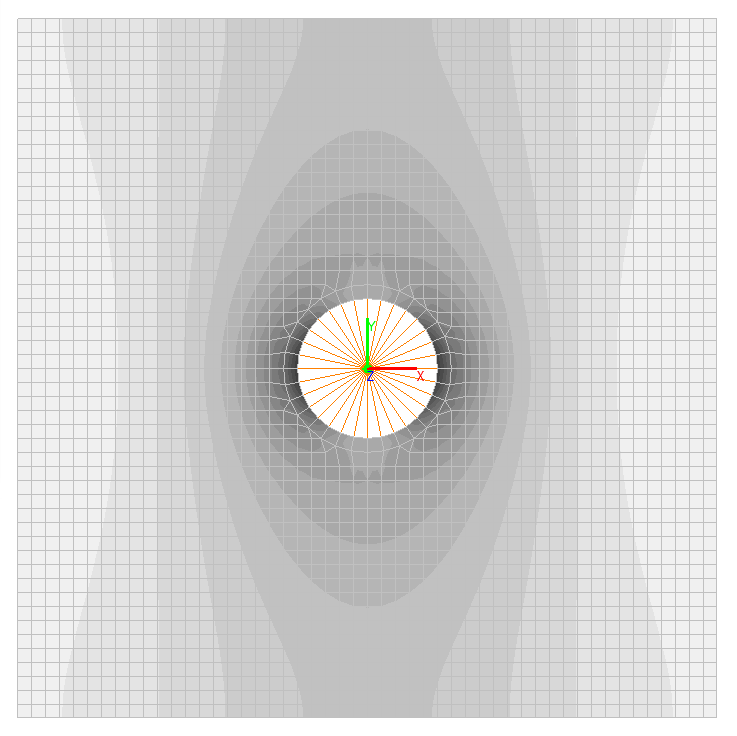
Изгибающие моменты M_x, Н∙ м/м

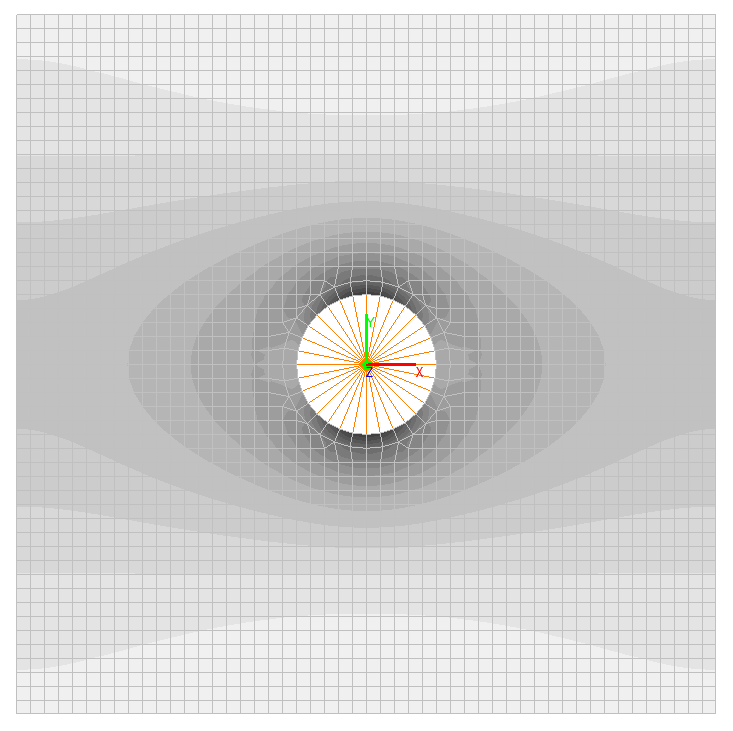
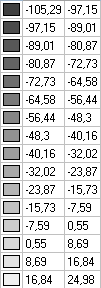
Изгибающие моменты M_y, Н∙ м/м

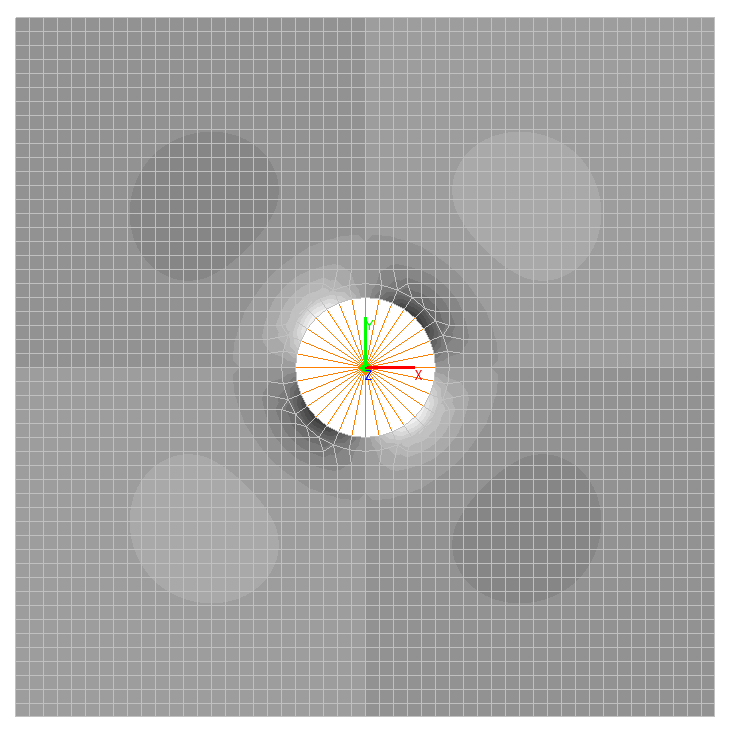
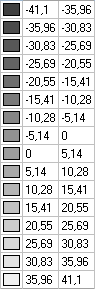
Изгибающие моменты M_xy, Н∙ м/м

Сравнение решений:

Изгибающий момент	Точка панели	Теория	SCAD	Отклонения
M_x = M_y	x = a/2, y = a/2	18.2500	17.8300	2.30
M_x	x = a/2, y = 0	24.9375	24.9800	0.17
M_y	x = a/2, y = 0	-10.0625	-10.1400	0.77
M_x	x = c, y = 0	-105.1250	-105.2900	0.16

Замечания: При аналитическом решении изгибающие моменты M_x, M_y в характерных точках квадратной панели безбалочного перекрытия определяются по следующим формулам:

M = β∙q∙a².

Коэффициенты β для вычисления изгибающих моментов при c = 0.1∙a и υ = 0.2

Изгибающий момент	Точка панели	β
M_x = M_y	x = a/2, y = a/2	0.0292
M_x	x = a/2, y = 0	0.0399
M_y	x = a/2, y = 0	-0.0161
M_x	x = c, y = 0	-0.1682