Плоская рама под действием равномерно распределенного мгновенного импульса
Цель: Определение напряженно-деформированного состояния плоской рамы от воздействия равномерно распределенного мгновенного импульса.
Файл с исходными данными: DI_F.SPR
Формулировка задачи: Плоская однопролетная трехъярусная рама, защемленная по стойкам, с равномерно распределенной массой на стойках m1 и ригелях m2 нагружается мгновенным импульсом s равномерно распределенным по контуру нижнего яруса. Определить амплитудные значения изгибающего момента M в ригеле нижнего яруса по сечению сопряжения с левой стойкой при учете следующего допущения, принятого при выводе аналитического решения:
принимается отсутствие линейных перемещений узлов сопряжения стоек с ригелями при симметричном нагружении симметричной расчетной схемы и пренебрежении продольными деформациями элементов конструкции рамы.
Ссылки: И. М. Рабинович, А. П. Синицын, О.В. Лужин, В.М. Теренин, Расчет сооружений на импульсные воздействия, Москва, Стройиздат, 1970, стр. 91;
Б. Г. Коренев, И. М. Рабинович, Динамический расчет зданий и сооружений (Справочник проектировщика), Москва, Стройиздат, 1984, стр. 79.
Исходные данные:
| E = 2.1·107 тс/м2 | - модуль упругости; |
| h = 6.0 м | - высота стоек рамы; |
| I1 = 1·10-4 м4 | - момент инерции поперечного сечения стоек рамы; |
| F1 = 2·10-1 м2 | - площадь поперечного сечения стоек рамы; |
| m1 = 0.0204 тс·с2/м2 | - значение равномерно распределенной массы на стойках рамы; |
| l = 5.0 м | - длина пролета ригелей рамы; |
| I2 = 2·10-4 м4 | - момент инерции поперечного сечения ригелей рамы; |
| F2 = 4·10-1 м2 | - площадь поперечного сечения ригелей рамы; |
| m2 = 0.0510 тс·с2/м2 | - значение равномерно распределенной массы на ригелях рамы; |
| s = 0.3· тс∙с/м | - значение равномерно распределенного мгновенного импульса; |
| g = 9.81 м/с2 | - значение ускорения свободного падения. |
Конечноэлементная модель: Расчетная схема – плоская рама, 102 стержневых элемента типа 2.
Сетка конечных элементов разбита по длинам продольных осей стоек и ригелей рамы с шагом 0.5 м. Обеспечение граничных условий по опорным узлам стоек нижнего яруса достигается за счет наложения связей по направлениям степеней свободы: X, Z, UY. Обеспечение граничных условий в узлах сопряжения стоек с ригелями по допущению, принятому при выводе аналитического решения достигается за счет наложения связей по направлениям степеней свободы: X, Z. Обеспечение граничных условий в узлах середин пролетов ригелей по допущению, принятому при выводе аналитического решения достигается за счет наложения связей по направлениям степеней свободы: X, UY. Распределенная масса задается преобразованием статической нагрузки на стойках m1·g и ригелях m2·g рамы. Воздействие распределенного мгновенного импульса приводится к ряду узловых воздействий со значениями 0.5·s. Количество узлов в расчетной схеме – 101.
Результаты решения в SCAD:
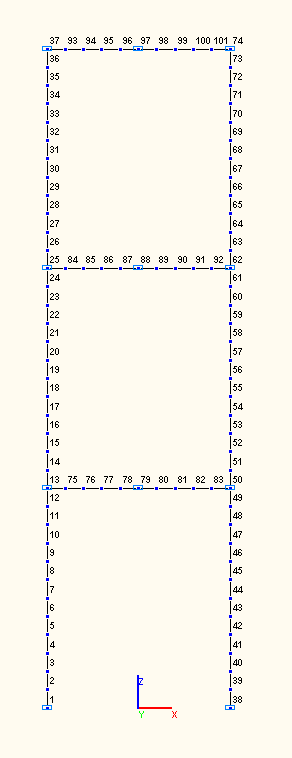
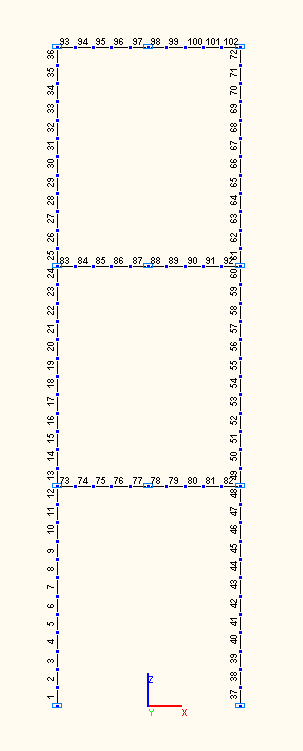
Расчетная схема
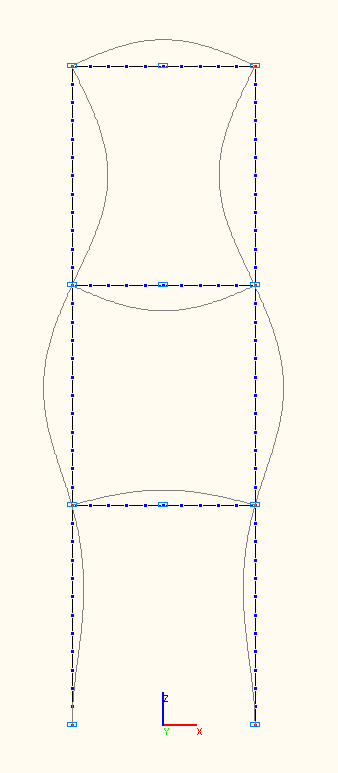
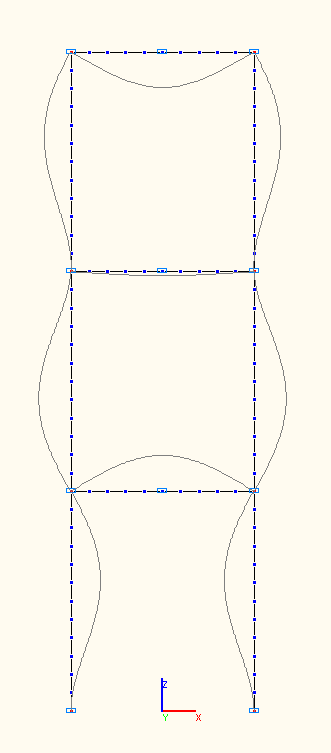
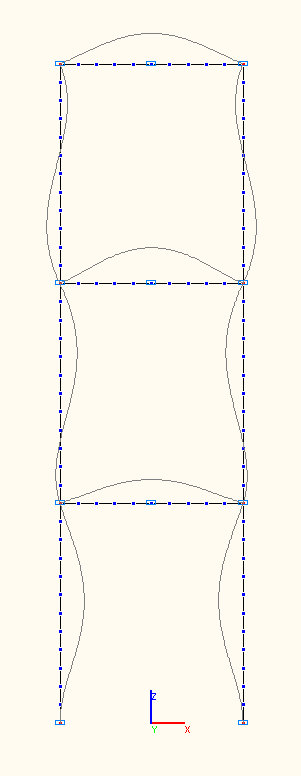
1-я, 2-я, 3-я собственные формы колебаний
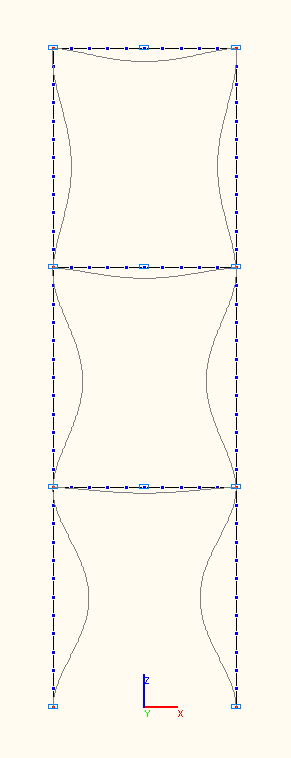
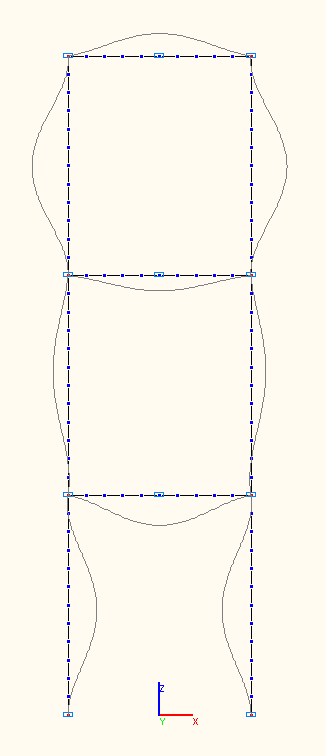
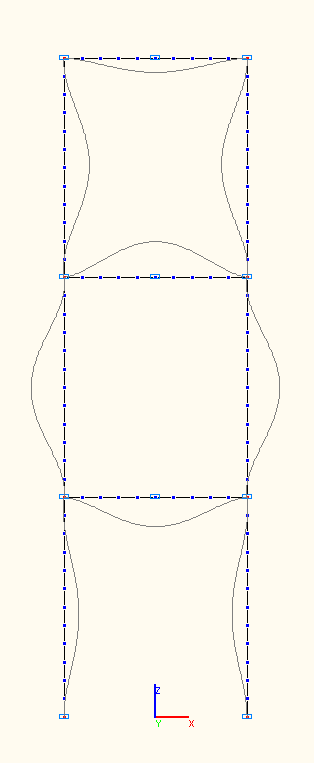
7-я, 8-я, 9-я собственные формы колебаний
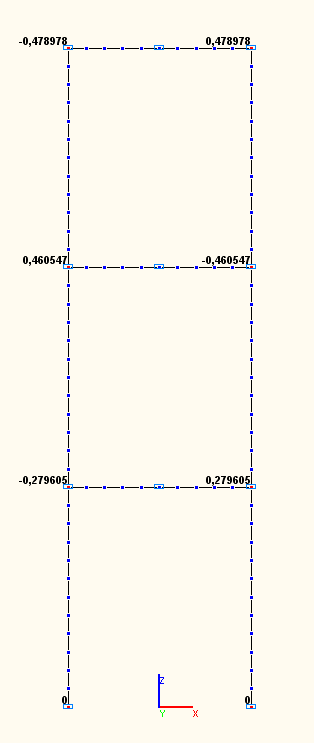
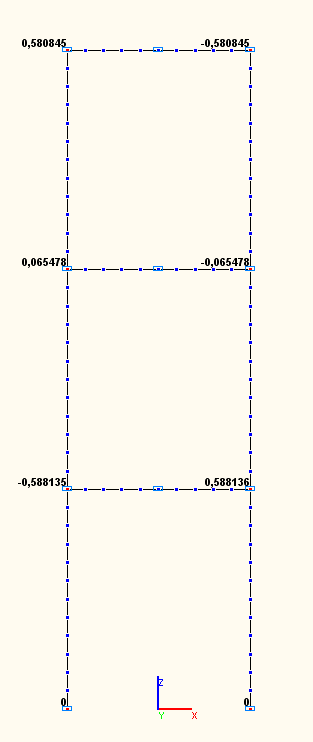
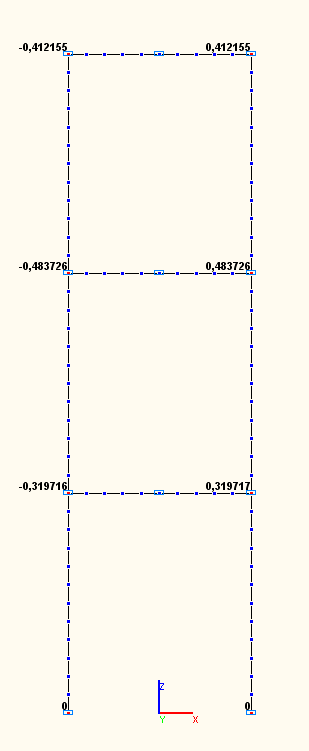
Амплитудные значения угловых перемещений UYij (рад) в узлах сопряжений ригелей со стойками по 1-й, 2-й, 3-й собственным формам колебаний (модальный анализ)
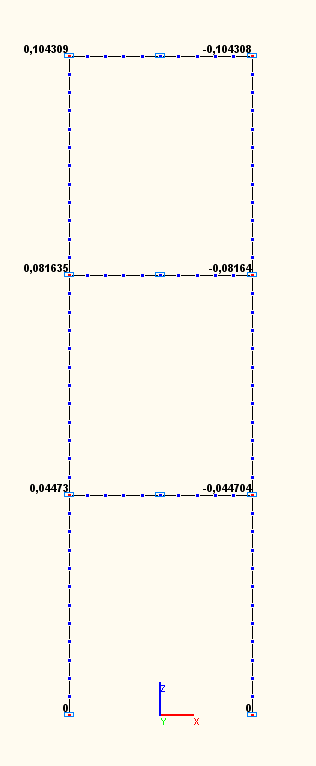
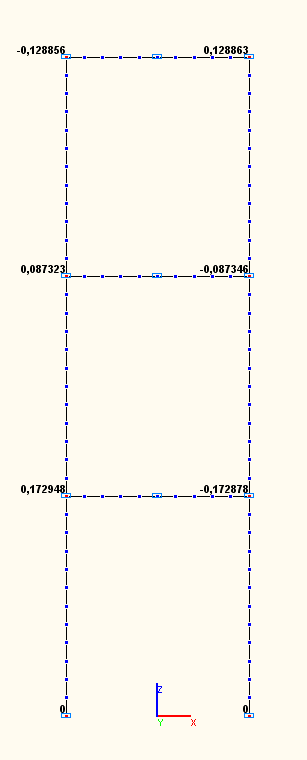
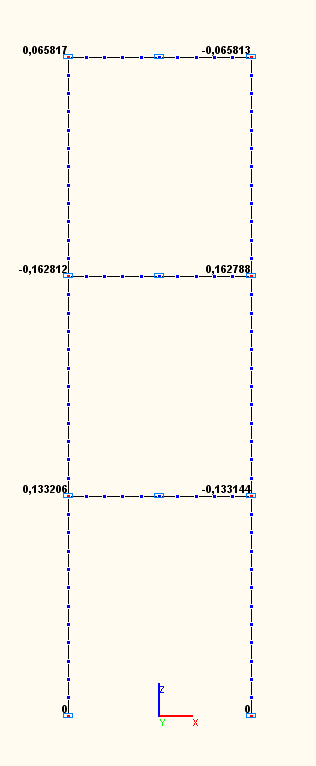
Амплитудные значения угловых перемещений UYij (рад)
в узлах сопряжений ригелей со стойками по 7-й, 8-й, 9-й собственным формам колебаний (модальный анализ)
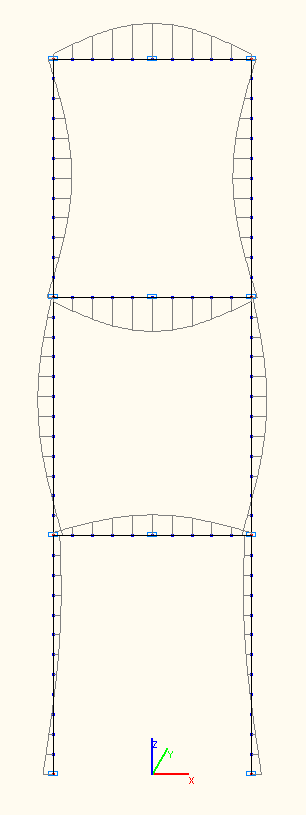
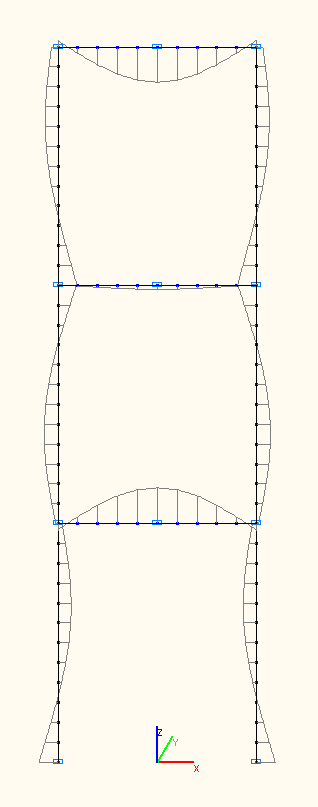
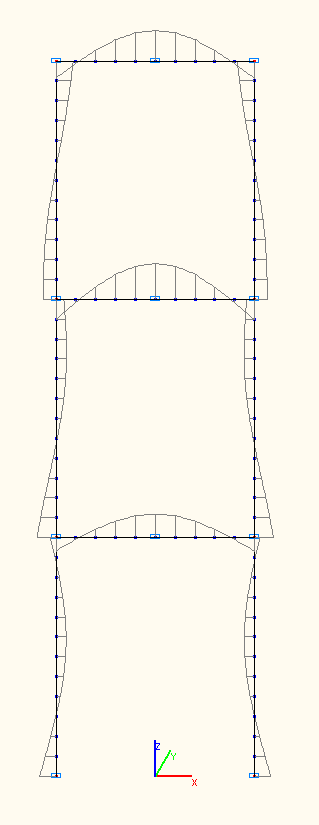
Эпюры изгибающих моментов при амплитудных значениях Mi (тс·м) по 1-й, 2-й, 3-й собственным формам колебаний
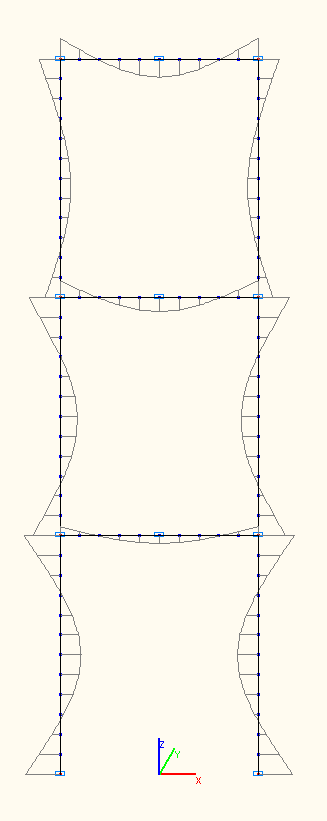
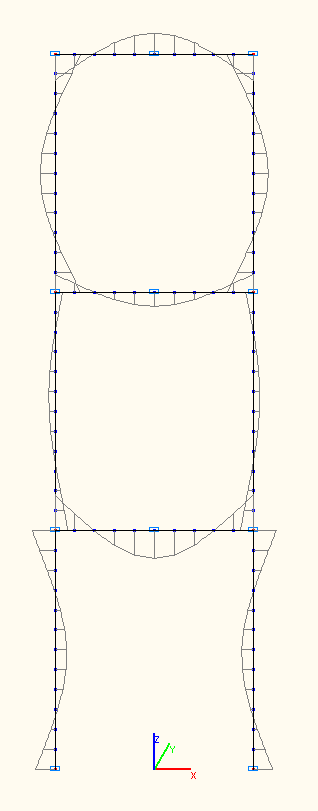
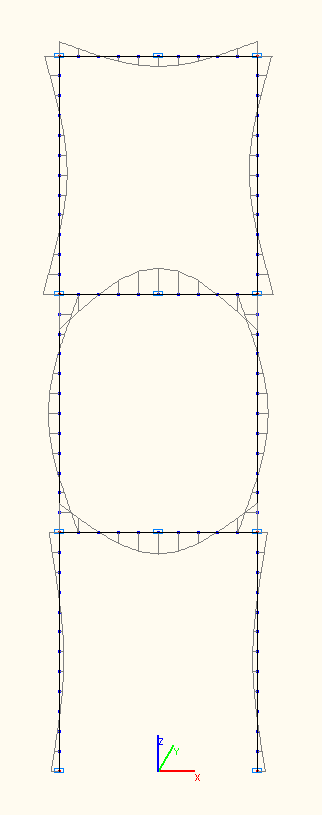
Эпюры изгибающих моментов при амплитудных значениях Mi (тс·м) по 7-й, 8-й, 9-й собственным формам колебаний
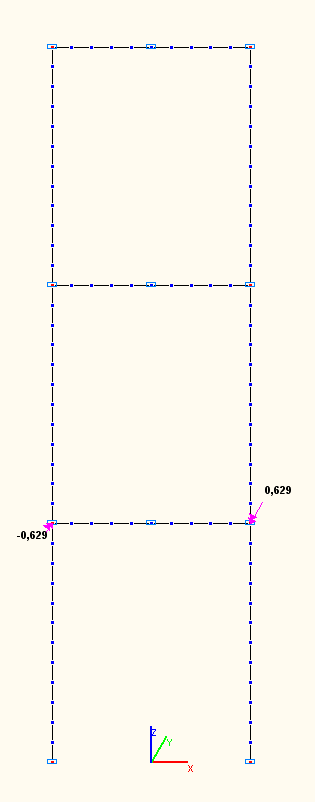
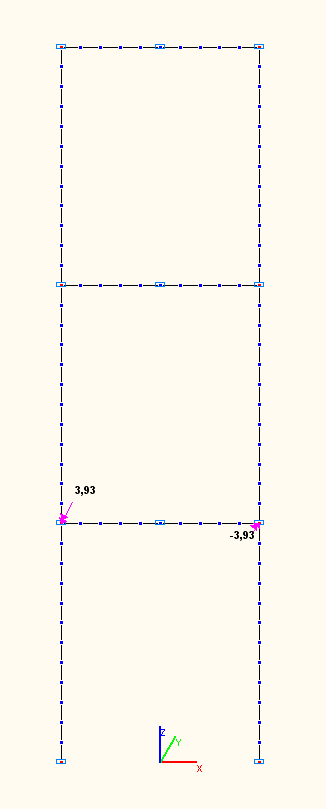
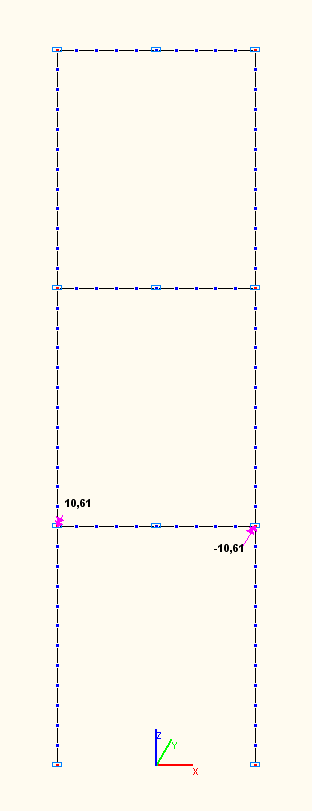
Амплитудные значения изгибающих моментов Mi (тс·м) в ригеле нижнего яруса по сечениям сопряжений со стойками по 1-й, 2-й, 3-й собственным формам колебаний
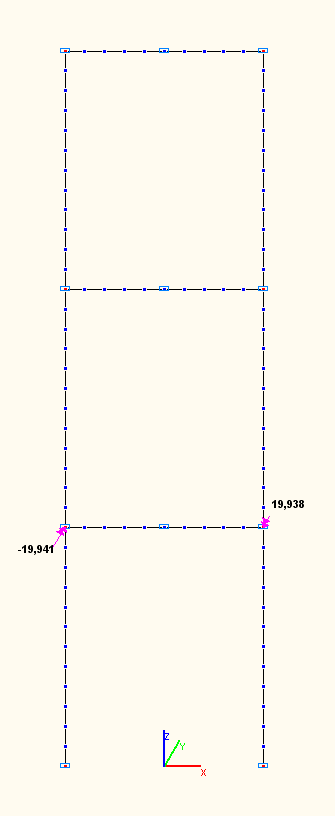
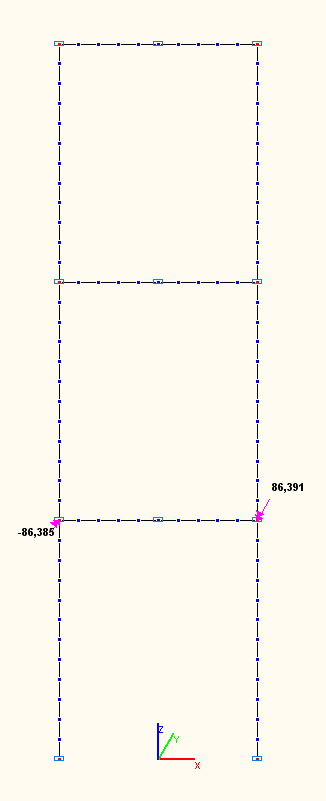
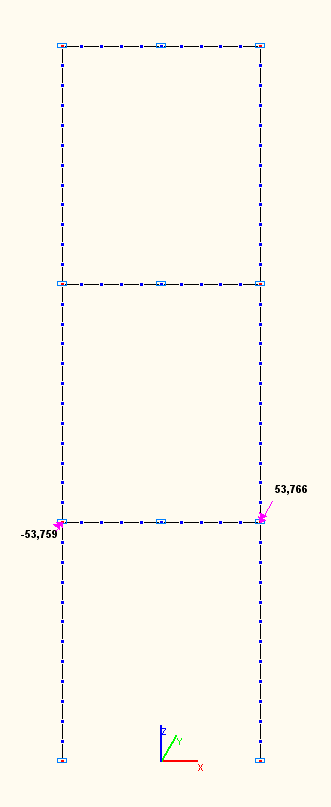
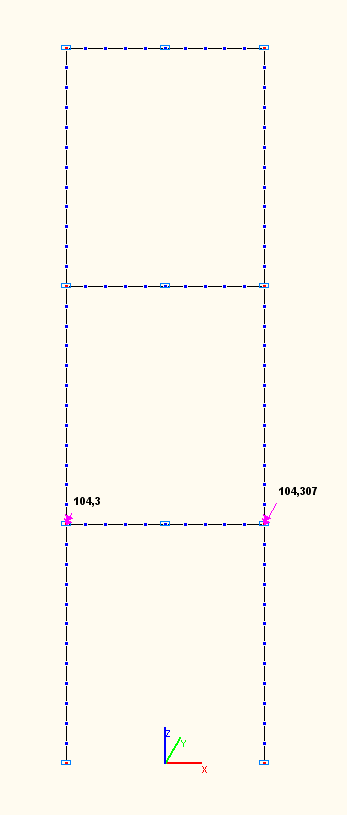
Амплитудные значения изгибающих моментов Mi (тс·м) в ригеле нижнего яруса по сечениям сопряжений со стойками по 7-й, 8-й, 9-й собственным формам колебаний
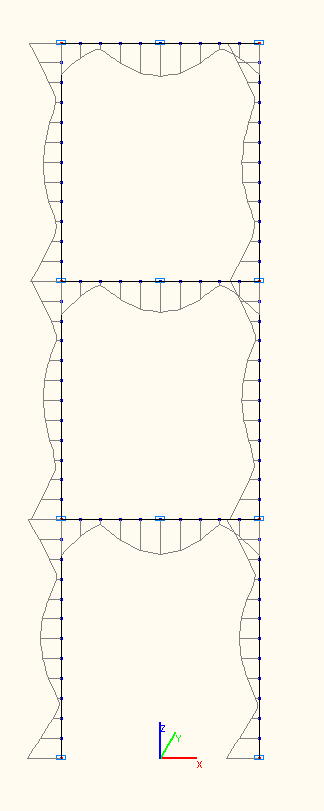
Эпюра изгибающих моментов при амплитудных значениях M (тс·м)
от суммарной импульсной нагрузки
Амплитудные значения изгибающих моментов M (тс·м)
в ригеле нижнего яруса по сечениям сопряжений со стойками от суммарной импульсной нагрузки
Сравнение решений:
Периоды собственных колебаний T, с
|
Форма колебаний |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
1 |
0.060607 |
0.060607 |
0.00 |
|
2 |
0.049785 |
0.049785 |
0.00 |
|
3 |
0.040435 |
0.040436 |
0.00 |
|
7 |
0.030924 |
0.030925 |
0.00 |
|
8 |
0.028903 |
0.028904 |
0.00 |
|
9 |
0.027787 |
0.027788 |
0.00 |
Амплитудные значения угловых перемещений UYij (рад)
в узлах сопряжений ригелей со стойками по 1-й, 2-й, 3-й, 7-й, 8-й, 9-й собственным формам колебаний (модальный анализ)
|
Форма колебаний |
Ярус |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 |
1 |
+0.583753 |
-0.279605 / -0.478978 = = +0.583753 |
0.00 |
|
1 |
2 |
-0.961520 |
+0.460547 / -0.478978 = = -0.961520 |
0.00 |
|
1 |
3 |
+1.000000 |
-0.478978 / -0.478978 = = +1.000000 |
0.00 |
|
2 |
1 |
-1.012550 |
-0.588135 / +0.580845 = = -1.012551 |
0.00 |
|
2 |
2 |
+0.112727 |
+0.065478 / +0.580845 = = +0.112729 |
0.00 |
|
2 |
3 |
+1.000000 |
+0.580845 / +0.580845 = = +1.000000 |
0.00 |
|
3 |
1 |
+0.775708 |
-0.319716 / -0.412155 = = +0.775718 |
0.00 |
|
3 |
2 |
+1.173640 |
-0.483726 / -0.412155 = = +1.173651 |
0.00 |
|
3 |
3 |
+1.000000 |
-0.412155 / -0.412155 = = +1.000000 |
0.00 |
|
7 |
1 |
+0.428722 |
+0.044730 / +0.104309 = = +0.428822 |
0.00 |
|
7 |
2 |
+0.782640 |
+0.081635 / +0.104309 = = +0.782627 |
0.00 |
|
7 |
3 |
+1.000000 |
+0.044730 / +0.104309 = = +1.000000 |
0.00 |
|
8 |
1 |
-1.342142 |
+0.172948 / -0.128856 = = -1.342180 |
0.00 |
|
8 |
2 |
-0,677645 |
+0.087323 / -0.128856 = = -0,677679 |
0.00 |
|
8 |
3 |
+1.000000 |
-0.128856 / -0.128856 = = +1.000000 |
0.00 |
|
9 |
1 |
+2.023786 |
+0.133206 / +0.065817 = = +2.023884 |
0.00 |
|
9 |
2 |
-2.473762 |
-0.162812 / +0.065817 = = -2.473707 |
0.00 |
|
9 |
3 |
+1.000000 |
+0.065817 / +0.065817 = = +1.000000 |
0.00 |
Амплитудные значения изгибающих моментов Mi (тс·м)
в ригеле нижнего яруса по сечению сопряжения с левой стойкой по 1-й, 2-й, 3-й, 7-й, 8-й, 9-й собственным формам колебаний
|
Форма колебаний |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
1 |
+0.629 |
-0.629 |
0.00 |
|
2 |
-3.931 |
+3.930 |
0.03 |
|
3 |
-10.611 |
+10.610 |
0.01 |
|
7 |
+19.939 |
-19.941 |
0.01 |
|
8 |
+86.385 |
-86.385 |
0.00 |
|
9 |
+53.755 |
-53.759 |
0.01 |
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Амплитудные значения изгибающего момента M в ригеле нижнего яруса по сечению сопряжения с левой стойкой от суммарной импульсной нагрузки, тс·м |
+165.576 (+173.075) |
+175.241 |
5.84 (1.25) |
Теоретическое значение изгибающего момента в ригеле соответствует моменту времени t = 0.036 с от начала воздействия импульсной нагрузки;
В скобках приведено теоретическое значение изгибающего момента в ригеле, определенное с учетом сдвига фаз гармоник.
Замечания: При аналитическом решении периоды собственных колебаний T, амплитудные значения угловых перемещений UYij в узлах сопряжений ригелей со стойками при модальном анализе, амплитудные значения изгибающих моментов в ригеле нижнего яруса по сечению сопряжения с левой стойкой по собственным формам колебаний Mi и от суммарной импульсной нагрузки M определяются по формулам:
\[ T_{i} =\frac{2\cdot \pi }{\omega_{i} }; \quad \omega_{i} =\frac{\lambda_{i}^{2}}{h^{2}}\cdot \sqrt {\frac{E\cdot I_{1} }{m_{1} }} ; \]
λi – определяются из выражения:
\[ \left\{ 4\cdot \left[ {ch( \lambda )\cdot \sin ( \lambda )-sh( \lambda)\cdot \cos ( \lambda )} \right]^{3}-3\cdot \left[ {sh( \lambda)-\sin ( \lambda)} \right]^{2}\cdot \left[ {ch( \lambda)\cdot \sin ( \lambda)-sh( \lambda )\cdot \cos ( \lambda )} \right] \right\} / {\left[ {1-ch( \lambda)\cdot \cos( \lambda)} \right]^{3}}+ \] \[ +\beta^{2}\cdot \alpha^{2}\cdot \left\{ {5\cdot \left[ {ch( \lambda )\cdot \sin ( \lambda )-sh( \lambda )\cdot \cos ( \lambda )} \right]\cdot \left[ {ch( {\alpha \cdot \lambda } )\cdot \sin ( {\alpha \cdot \lambda } )-sh( {\alpha \cdot \lambda } )\cdot \cos ( {\alpha \cdot \lambda } } \right]^{2}} \right.+ \] \[ +5\cdot \left[ {sh\left( {\alpha \cdot \lambda } \right)-\sin \left( {\alpha \cdot \lambda } \right)} \right]^{2}\cdot \left[ {ch\left( \lambda \right)\cdot \sin \left( \lambda \right)-sh\left( \lambda \right)\cdot \cos \left( \lambda \right)} \right]- \] \[ \left. -10\cdot \left[ sh( {\alpha \cdot \lambda } )-\sin ( {\alpha \cdot \lambda } ) \right]\cdot \left[ ch( \lambda )\cdot \sin ( \lambda )-sh( \lambda )\cdot \cos ( \lambda ) \right]\cdot \left[ ch( {\alpha \cdot \lambda } )\cdot \sin ( {\alpha \cdot \lambda } )-sh( {\alpha \cdot \lambda } )\cdot \cos ( {\alpha \cdot \lambda } ) \right] \right\} / \] \[ / \left\{ \left[ {1-ch( \lambda )\cdot \cos ( \lambda )} \right]\cdot \left[ 1-ch( {\alpha \cdot \lambda )\cdot \cos ( \alpha \cdot \lambda )} \right]^{2} \right\}+ \] \[ +\beta\cdot \alpha\cdot \left\{ {8\cdot \left[ {ch( \lambda )\cdot \sin ( \lambda )-sh( \lambda )\cdot \cos ( \lambda )} \right]^2\cdot \left[ {ch( {\alpha \cdot \lambda } )\cdot \sin ( {\alpha \cdot \lambda } )-sh( {\alpha \cdot \lambda } )\cdot \cos ( {\alpha \cdot \lambda } } \right]} \right.- \] \[ -8\cdot \left[ {sh\left( {\alpha \cdot \lambda } \right)-\sin \left( {\alpha \cdot \lambda } \right)} \right]\cdot \left[ {ch\left( \lambda \right)\cdot \sin \left( \lambda \right)-sh\left( \lambda \right)\cdot \cos \left( \lambda \right)} \right]^{2}- \] \[ \left. -2\cdot \left[ sh( \lambda )-\sin ( \lambda ) \right]^{2}\cdot \left[ ch( {\alpha \cdot \lambda } )\cdot \sin ( {\alpha \cdot \lambda } )-sh( {\alpha \cdot \lambda } )\cdot \cos ( {\alpha \cdot \lambda } ) \right]+2\cdot \left[ sh( \lambda )-\sin ( \lambda ) \right]^{2}\cdot \left[ sh( {\alpha \cdot \lambda } )-\sin (\alpha \cdot \lambda) \right] \right\} / \] \[ / \left\{ \left[ {1-ch( \lambda )\cdot \cos ( \lambda )} \right]^{2}\cdot \left[ 1-ch( {\alpha \cdot \lambda )\cdot \cos ( \alpha \cdot \lambda )} \right] \right\}+ \] \[ + \beta^{3}\cdot \alpha^{3}\cdot \left\{ \left[ ch( \alpha \cdot \lambda )\cdot \sin( \alpha \cdot \lambda )-sh( \alpha \cdot \lambda)\cdot \cos ( \alpha \cdot \lambda ) \right]^{3} +3\cdot \left[ sh( \alpha \cdot \lambda )-\sin (\alpha \cdot \lambda) \right]^{2}\cdot \left[ ch(\alpha \cdot \lambda)\cdot \sin (\alpha \cdot \lambda)-sh( \alpha \cdot \lambda )\cdot \cos (\alpha \cdot \lambda) \right]- \right. \] \[ \left. -3\cdot \left[ {sh(\alpha \cdot \lambda)-\sin (\alpha \cdot \lambda)} \right]\cdot \left[ ch( {\alpha \cdot \lambda } )\cdot \sin (\alpha \cdot \lambda )-sh(\alpha \cdot \lambda)\cdot \cos (\alpha \cdot \lambda) \right]^{2}-\left[ {sh(\alpha \cdot \lambda } )-\sin (\alpha \cdot \lambda) \right]^{3} \right\} / \] \[ / \left\{ \left[ 1-ch( \alpha \cdot \lambda)\cdot \cos (\alpha \cdot \lambda ) \right]^{3} \right\} = 0, \quad где: \] \[ \alpha =\frac{l}{h}\cdot \sqrt[4]{\frac{m_{2} \cdot I_{1} }{m_{1} \cdot I_{2} }}, \quad \beta =\frac{h}{l}\cdot \frac{I_{2} }{I_{1} }; \] \[ UY_{i1} =\left\{ \left[ ch(\lambda_{i} )\cdot \sin (\lambda_{i})-sh(\lambda_{i})\cdot \cos (\lambda_{i}) \right] \cdot \left[ 1-ch(\alpha \cdot \lambda_{i})\cdot \cos (\alpha \cdot \lambda)_{i} \right]+ \right. \] \[ \left. +\beta \cdot \alpha \cdot \left[ \sin (\alpha \cdot \lambda_{i})\cdot \left[ ch(\alpha \cdot \lambda_{i})+1 \right] -sh( \alpha \cdot \lambda_{i})\cdot \left[ \cos (\alpha \cdot \lambda_{i})+1 \right] \right] \cdot \left[ 1-ch (\lambda_{i} )\cdot \cos ( \lambda )_{i} \right] \right\} \cdot UY_{i3} / \] \[ / \left\{ 2\cdot \left[ ch( \lambda_{i})\cdot \sin (\lambda_{i}) -sh ( \lambda_{i})\cdot \cos (\lambda_{i}) \right] \cdot \left[ 1-ch (\alpha \cdot \lambda_{i})\cdot \cos (\alpha \cdot \lambda)_{i} \right] + \right. \] \[ \left. +\beta \cdot \alpha \cdot \left[ \sin (\alpha \cdot \lambda_{i})\cdot \left[ ch(\alpha \cdot \lambda_{i})+1 \right] -sh( \alpha \cdot \lambda_{i})\cdot \left[ \cos (\alpha \cdot \lambda_{i})+1 \right] \right] \cdot \left[ 1-ch (\lambda_{i} )\cdot \cos ( \lambda )_{i} \right] \right\} , \] \[ UY_{i2} =\left\{ \left[ ch(\lambda_{i} )\cdot \sin (\lambda_{i})-sh(\lambda_{i})\cdot \cos (\lambda_{i}) \right] \cdot \left[ 1-ch(\alpha \cdot \lambda_{i})\cdot \cos (\alpha \cdot \lambda)_{i} \right]+ \right. \] \[ \left. +\beta \cdot \alpha \cdot \left[ \sin (\alpha \cdot \lambda_{i})\cdot \left[ ch(\alpha \cdot \lambda_{i})+1 \right] -sh( \alpha \cdot \lambda_{i})\cdot \left[ \cos (\alpha \cdot \lambda_{i})+1 \right] \right] \cdot \left[ 1-ch (\lambda_{i} )\cdot \cos ( \lambda )_{i} \right] \right\} \cdot UY_{i3} / \] \[ / \left\{ \cdot \left[ ch( \lambda_{i})\cdot \sin (\lambda_{i}) \right] \cdot \left[ 1-ch (\alpha \cdot \lambda_{i})\cdot \cos (\alpha \cdot \lambda)_{i} \right] + \right\}, \] \[ UY_{i3} =1.0; \] \[ M=\sum\limits_{i=1}^N {M_{i} \cdot \sin \left( {\omega_{i} \cdot t} \right)} \quad - \quad без \quad учета \quad сдвига \quad фаз \quad гармоник, \] \[ t \quad - \quad определяются \quad из \quad выражения: \] \[ \sum\limits_{i=1}^N {\omega_{i} \cdot M_{i} \cdot \cos \left( {\omega_{i} \cdot t} \right)} =0, \] \[ M=\sum\limits_{i=1}^{q-1} {\left| {M_{i} } \right|\cdot \sin \left( {\frac{\pi \cdot \omega_{i} }{2\cdot \omega_{q} }} \right)+} \sum\limits_{i=q}^N {\left| {M_{i} } \right|} , \quad при \quad \left| {M_{q} } \right|>\left| {M_{i} } \right|\quad, \quad\left( {i\ne q} \right)\quad - с \quad учетом сдвига \quad фаз \quad гармоник, \quad где: \] \[ M_{i} =A_{i} \cdot M_{gi} , \quad A_{i} =\frac{A_{i1} }{A_{i2} \cdot \omega_{i} }, \] \[ A_{i1} =\frac{2\cdot s\cdot UY_{i1} }{\lambda_{i}^{2}}\cdot \left\{ {h^{2}\cdot \frac{ch\left( {\lambda_{i} } \right)-\cos \left( {\lambda_{i} } \right)-sh\left( {\lambda_{i} } \right)\cdot \sin \left( {\lambda_{i} } \right)}{1-ch\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)}-\frac{l^{2}}{\alpha^{2}}\cdot \frac{ch\left( {\alpha \cdot \lambda _{i} } \right)-\cos \left( {\alpha \cdot \lambda_{i} } \right)-sh\left( {\alpha \cdot \lambda_{i} } \right)\cdot \sin \left( {\alpha \cdot \lambda _{i} } \right)}{1-ch\left( {\alpha \cdot \lambda_{i} } \right)\cdot \cos \left( {\alpha \cdot \lambda_{i} } \right)}} \right\}, \] \[ A_{i2} =\frac{m_{1} \cdot h^{3}}{\lambda_{i}^{3}}\cdot \left\{ {\left( {UY_{i1}^{2}+UY_{i2}^{2}+\frac{UY_{i3}^{2}}{2}} \right)} \right.\cdot \left[ {\lambda_{i} \cdot \frac{\left[ {sh\left( {\lambda_{i} } \right)-\sin \left( {\lambda_{i} } \right)} \right]^{2}}{\left[ {1-ch\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)} \right]^{2}}-\frac{ch\left( {\lambda_{i} } \right)\cdot \sin \left( {\lambda_{i} } \right)-sh\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)}{1-ch\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)}} \right]+ \] \[ \left. {\left( {UY_{i1} \cdot UY_{i2} +UY_{i2} \cdot UY_{i3} } \right)\cdot \left[ {\lambda_{i} \cdot \frac{\left[ {sh\left( {\lambda_{i} } \right)-\sin \left( {\lambda_{i} } \right)} \right]\cdot \left[ {ch\left( {\lambda_{i} } \right)\cdot \sin \left( {\lambda_{i} } \right)-sh\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)} \right]}{\left[ {1-ch\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)} \right]^{2}}-\lambda_{i} \cdot \frac{ch\left( {\lambda_{i} } \right)-\cos \left( {\lambda_{i} } \right)}{1-ch\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)}-\frac{sh\left( {\lambda_{i} } \right)-\sin \left( {\lambda_{i} } \right)}{1-ch\left( {\lambda_{i} } \right)\cdot \cos \left( {\lambda_{i} } \right)}} \right]} \right\} + \] \[ \frac{m_2\cdot l^3}{2\cdot\alpha^3\lambda_i^3} \left\{ \left(UY_{i1}^2+UY_{i2}^2+UY_{i3}^2 \right)\cdot \left[ \alpha\cdot\lambda_i \frac{\left[sh(\alpha\cdot\lambda_i)-\sin(\alpha\cdot\lambda_i)\right]^2}{\left[1-ch(\alpha\cdot\lambda_i)\cdot\cos(\alpha\cdot\lambda_i)\right]^2} -\frac{ch(\alpha\cdot\lambda_i)\cdot\sin(\alpha\cdot\lambda_i)-sh(\alpha\cdot\lambda_i)\cdot\cos(\alpha\cdot\lambda_i)}{1-ch(\alpha\cdot\lambda_i)\cdot\cos(\alpha\cdot\lambda_i)}- \right. \right. \] \[ -\alpha \cdot \lambda_{i} \cdot \frac{\left[ {sh\left( {\alpha \cdot \lambda_{i} } \right)-\sin \left( {\alpha \cdot \lambda_{i} } \right)} \right]\cdot \left[ {ch\left( {\alpha \cdot \lambda_{i} } \right)\cdot \sin \left( {\alpha \cdot \lambda_{i} } \right)-sh\left( {\alpha \cdot \lambda _{i} } \right)\cdot \cos \left( {\alpha \cdot \lambda_{i} } \right)} \right]}{\left[ {1-ch\left( {\alpha \cdot \lambda_{i} } \right)\cdot \cos \left( {\alpha \cdot \lambda_{i} } \right)} \right]^{2}}+\alpha \cdot \lambda_{i} \cdot \frac{ch\left( {\alpha \cdot \lambda_{i} } \right)-\cos \left( {\alpha \cdot \lambda_{i} } \right)}{1-ch\left( {\alpha \cdot \lambda_{i} } \right)\cdot \cos \left( {\alpha \cdot \lambda_{i} } \right)}+ \] \[ \left. {\left. {+\frac{sh\left( {\alpha \cdot \lambda_{i} } \right)-\sin \left( {\alpha \cdot \lambda_{i} } \right)}{1-ch\left( {\alpha \cdot \lambda_{i} } \right)\cdot \cos \left( {\alpha \cdot \lambda_{i} } \right)}} \right]} \right\} . \] \[ M_{gi} =\frac{E\cdot l_{2} }{l}\cdot \alpha \cdot \lambda_{i} \cdot \frac{\sin \left( {\alpha \cdot \lambda_{i} } \right)\cdot \left( {ch\left( {\alpha \cdot \lambda_{i} } \right)+1} \right)-sh\left( {\alpha \cdot \lambda_{i} } \right)\cdot \left( {\cos \left( {\alpha \cdot \lambda_{i} } \right)+1} \right)}{1-ch\left( {\alpha \cdot \lambda_{i} } \right)\cdot \cos \left( {\alpha \cdot \lambda_{i} } \right)}\cdot UY_{i2} \]
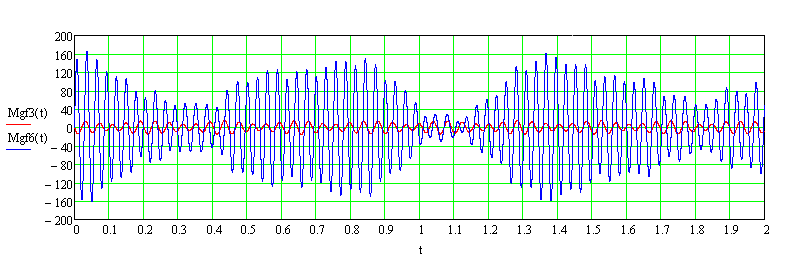
График изменения значений изгибающих моментов M (тс·м) во времени t (с)
в ригеле нижнего яруса по сечениям сопряжений со стойками от суммарной импульсной нагрузки с учетом по 3-х и 6-ти симметричных собственных форм колебаний
Существенное расхождение в результатах (>5%) в амплитудных значениях изгибающего момента связано с тем, что в источнике Расчет сооружений на импульсные воздействия суммирование по формам осуществляется без учета сдвига фаз. В более поздних рекомендациях уже есть требование учета сдвига фаз. В этом случае расхождение с теорией составляет 1.25%.
