Упругое полупространство под действием равномерно распределенной по поверхности прямоугольной в плане поперечной нагрузки. Задача Лява.
Цель: Определение напряженно-деформированного состояния упругого полупространства от действия равномерно распределенной по поверхности прямоугольной в плане поперечной нагрузки в соответствии с объемной задачей теории упругости.
Имя файлов с исходными данными: Lave.SPR
Формулировка задачи: Упругое полупространство находится под воздействием равномерно распределенной по поверхности прямоугольной в плане поперечной нагрузки q. Определить:
- распределение нормальных напряжений σx, σy, σz по полупространству;
- распределение касательных напряжений τxy, τxz, τyz по полупространству;
- распределение перемещений u, v, w по полупространству.
Ссылки: З. Г. Тер-Мартиросян, Механика грунтов, Москва, МГСУ Издательство Ассоциации строительных вузов, 2009, стр. 204;
В.А. Флорин, Основы механики грунтов, Том 1, Ленинград, Государственное издательство литературы по строительству, архитектуре и строительным материалам, 1959, стр. 123;
В.А. Флорин, Основы механики грунтов, Том 2, Ленинград, Государственное издательство литературы по строительству, архитектуре и строительным материалам, 1959, стр. 24.
Исходные данные:
| E = 30000 кН/м2 | - модуль упругости полупространства; |
| m = 0.3 | - коэффициент Пуассона; |
| a = b = 2.0 м | - длина половины стороны прямоугольной в плане загруженной поверхности; |
| q = 100 кH/м2 | - равномерно распределенная по поверхности прямоугольной в плане поперечная нагрузка. |
Конечно-элементная модель: Рассчитывается параллелепипед со сторонами 96×96×48 м. Расчетная схема (представляет собой – часть параллелепипеда, отсеченную плоскостями симметрии XOZ и YOZ) – система общего вида, элементы упругого полупространства – 138253 20-и узловых изопараметрических объемных элементов типа 37. Первоначальная сетка конечных элементов полупространства в районе приложения нагрузки в плане и по глубине имеет шаг 0,25 м с последующим увеличением размеров конечных элементов по мере удаления от нее.
Направление выдачи внутренних усилий сориентировано по осям общей системы координат. Верхние грани элементов границы полупространства загружены поверхностной поперечной нагрузкой в плане в пределах 2a×2b = 4.0 м×4.0 м.
Краевые условия были определены следующим образом: на нижней и боковых поверхностях запрещены перемещения по нормали.
Количество узлов в расчетной схеме – 573985.
Результаты решения в SCAD

Расчетная схема

Деформированная схема поверхности упругого полупространства
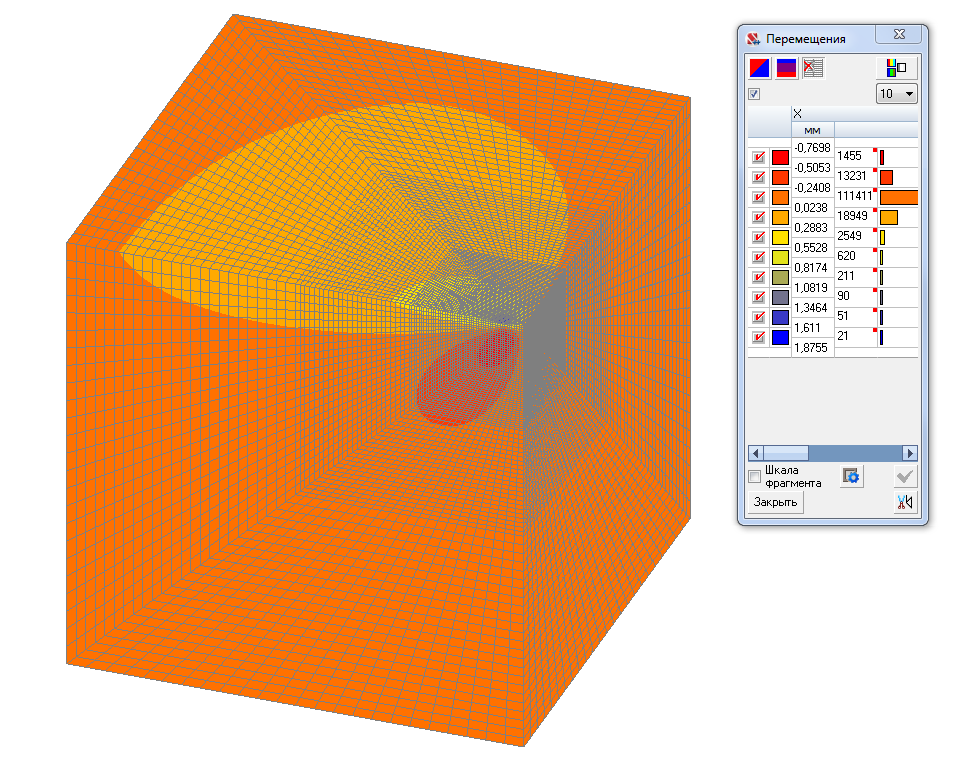
Значения горизонтальных перемещений u (мм)
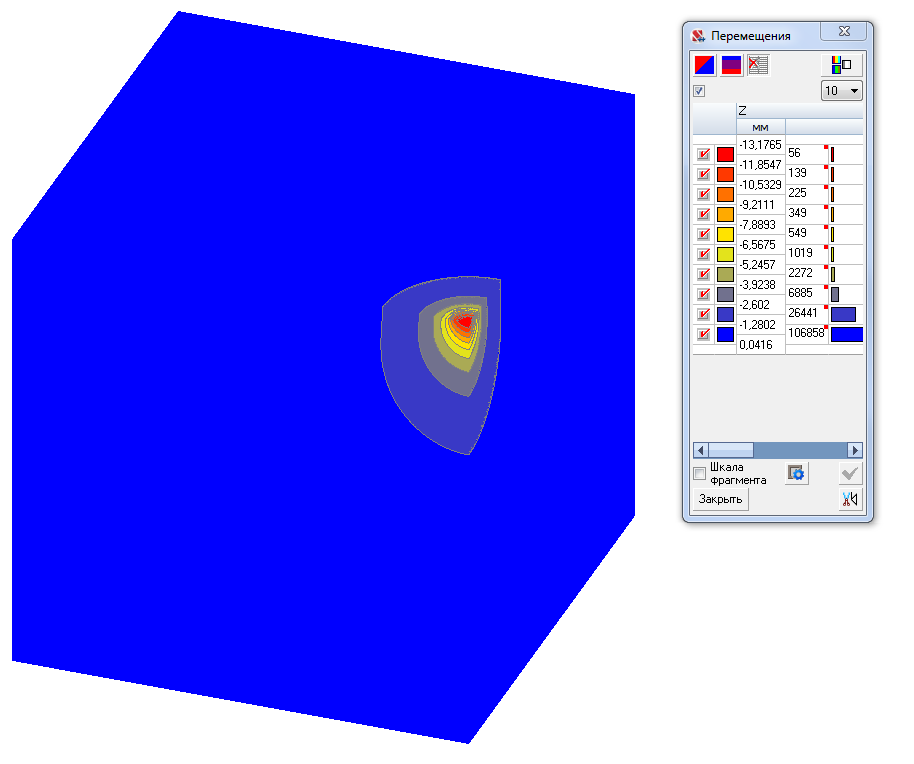
Значения вертикальных перемещений w (мм)
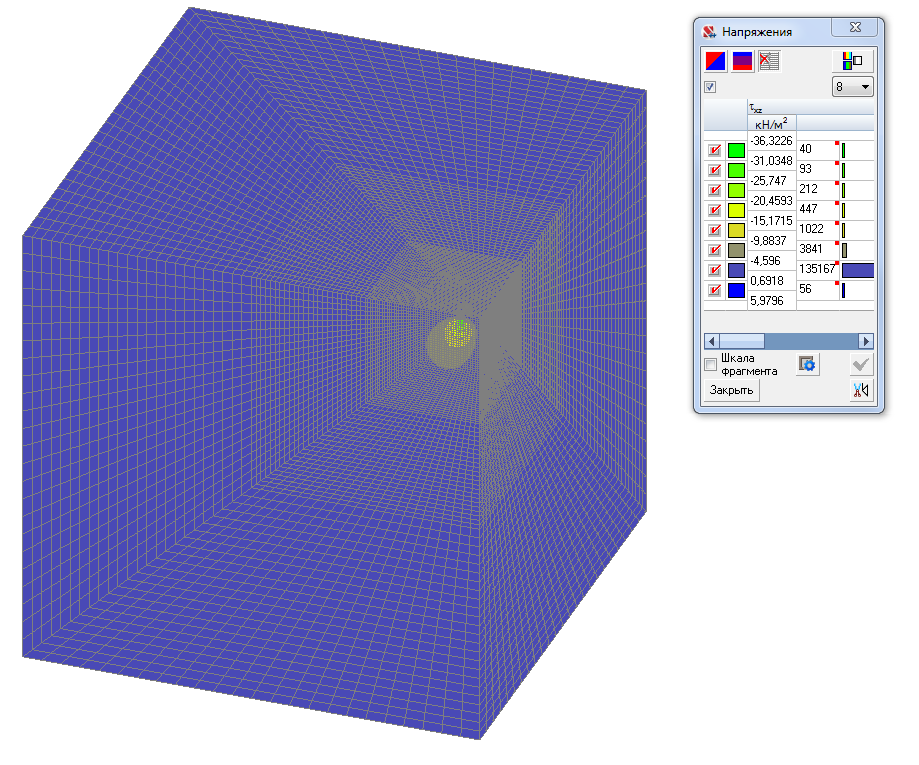
Значения вертикальных τxz касательных напряжений (т/м2)
Сравнение решений:
Решение задачи Лява 20-и узловыми
изопараметрическими элементами (мм, кН/м2)
|
Точка |
Параметр |
|
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|---|
|
(0,0,0) Узел 1 |
w |
мм |
-13,616 |
-13,177 |
3,2 |
|
σx=σy |
кН/м2 |
-80,0 |
-79,919 |
0,10 |
|
|
σz |
кН/м2 |
-100,0 |
-100,079 |
0,09 |
|
|
(0,0,-2) Узел 10005 |
w |
мм |
-9,017 |
-8,574 |
4,91 |
|
σx=σy |
кН/м2 |
-8,29 |
-8,189 |
1,21 |
|
|
σz |
кН/м2 |
-70,09 |
-70,109 |
0,03 |
|
|
(-2,2,-2) Узел 10213 |
u=v |
мм |
0,488 |
0,492 |
0,82 |
|
w |
мм |
-5,704 |
-5,262 |
7,75 |
|
|
σx=σy |
кН/м2 |
-7,56 |
-7,496 |
0,85 |
|
|
σz |
кН/м2 |
-23,25 |
-23,267 |
0,07 |
|
|
τxy |
кН/м2 |
-5,27 |
-5,288 |
0,34 |
|
|
τxz=τyz |
кН/м2 |
12,11 |
12,166 |
0,46 |
Замечания: При аналитическом решении распределение нормальных напряжений σx, σy, σz, касательных напряжений τxy, τxz, τyz и перемещений u, v, w по полупространству вычисляется по следующим формулам:
\[ \sigma_{x} (x,y,z)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\,(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{(x-a)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}-(y-b)^{2}+z^{2}} }} \right]} \right.+ \] \[ +2\cdot \mu \cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{z\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x-a)\cdot (y-b)}{\left[ {(x-a)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y+b)}{(x-a)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }} \right]- \] \[ -2\cdot \mu \cdot arctg\left[ {\frac{(x-a)\cdot (y+b)}{z\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }} \right]+\frac{z\cdot (x-a)\cdot (y+b)}{\left[ {(x-a)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{(x+a)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]- \] \[ -2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]+\frac{z\cdot (x+a)\cdot (y-b)}{\left[ {(x+a)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }- \] \[ -(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{(x+a)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]+ \] \[ \left. {+2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x+a)\cdot (y+b)}{\left[ {(x+a)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right\} . \] \[ \sigma_{y} (x,y,z)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\,(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{(y-b)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}-(y-b)^{2}+z^{2}} }} \right]} \right.+ \] \[ +2\cdot \mu \cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{z\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x-a)\cdot (y-b)}{\left[ {(y-b)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y+b)}{(y+b)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }} \right]+ \] \[ +\frac{z\cdot (x-a)\cdot (y+b)}{\left[ {(y+b)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{(y-b)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]- \] \[ +2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]+\frac{z\cdot (x+a)\cdot (y-b)}{\left[ {(y-b)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }- \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{(y+b)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]+ \] \[ \left. {+2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x+a)\cdot (y+b)}{\left[ {(y+b)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right\} . \]
\[ {\sigma_{z} \left( {x,y,z} \right)=\frac{q}{2\cdot \pi }\cdot \left\{ {\frac{z\cdot \left( {x-a} \right)\cdot \left( {y-b} \right)\cdot \left[ {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y-b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }+} \right.} \\ {+arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} {-\frac{z\cdot \left( {x-a} \right)\cdot \left( {y+b} \right)\cdot \left[ {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y+b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }-} \\ {-arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]-} {-\frac{z\cdot \left( {x+a} \right)\cdot \left( {y-b} \right)\cdot \left[ {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y-b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \\ {-arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} {+\frac{z\cdot \left( {x+a} \right)\cdot \left( {y+b} \right)\cdot \left[ {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y+b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }+} \\ {\left. {+arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \\ \]
\[ {\tau_{xy} \left( {x,y,z} \right)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]+} \right.} \\ {+\frac{z}{\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }+} {+\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\frac{z}{\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }+} {+\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\frac{z}{\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }-} {-\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]+} \\ {\left. {+\frac{z}{\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right\} .} \]
\[ {\tau_{xz} \left( {x,y,z} \right)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\frac{z^{2}\cdot \left( {y-b} \right)}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }+} \right.} \\ {+\frac{z^{2}\cdot \left( {y+b} \right)}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }+} {+\frac{z^{2}\cdot \left( {y-b} \right)}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }-} \\ {\left. {-\frac{z^{2}\cdot \left( {y+b} \right)}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right\} .} \]
\[ {u\left( {x,y,z} \right)=\frac{q\cdot \left( {1+\mu } \right)}{2\cdot \pi \cdot E}\cdot \left\{ {2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]-} \right.} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left( {\frac{y-b}{x-a}} \right)-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y-b} \right)}{\left( {x-a} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left( {\frac{y+b}{x-a}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y+b} \right)}{\left( {x-a} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left( {\frac{y-b}{x+a}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y-b} \right)}{\left( {x+a} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left( {\frac{y+b}{x+a}} \right)-} \\ {\left. {-\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y+b} \right)}{\left( {x+a} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \\ \]
\[ {v\left( {x,y,z} \right)=\frac{q\cdot \left( {1+\mu } \right)}{2\cdot \pi \cdot E}\cdot \left\{ {2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]-} \right.} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left( {\frac{x-a}{y-b}} \right)-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x-a} \right)}{\left( {y-b} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left( {\frac{x-a}{y+b}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x-a} \right)}{\left( {y+b} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left( {\frac{x+a}{y-b}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x+a} \right)}{\left( {y-b} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left( {\frac{x+a}{y+b}} \right)-} \\ {\left. {-\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x+a} \right)}{\left( {y+b} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \]
\[ {w\left( {x,y,z} \right)=\frac{q\cdot \left( {1+\mu } \right)}{2\cdot \pi \cdot E}\cdot \left\{ {-2\cdot \left( {1-\mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]-} \right.} \\ {-2\cdot \left( {1-\mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]+} \\ {\left. {+\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \]
