Амплитудно-частотная характеристика системы с одной степенью свободы

Цель: Построение амплитудно-частотной характеристики одномассовой упругой системы при гармоническом возбуждении.

Имя файлов с исходными данными: TestАЧХ.SPR

Формулировка задачи: Анализируется поведение одномассовой упругой системы при возбуждении силой меняющейся во времени по гармоническому закону с различной частотой возбуждения.

Ссылки: Пановко Я.Г. Введение в теорию механических колебаний — М.: Наука, 1980.

Исходные данные:

М = 10 кН	- вес массы;
С = 100 кН	- жесткость;
Р = 10 кН	- амплитудное значение силы;
ξ = 0.025	- параметр затухания (в долях от критического).

Конечноэлементная модель: Один узел, в котором задана точечная масса, поддержан одноузловой упругой связью (конечный элемент типа 51).

Результаты решения в SCAD

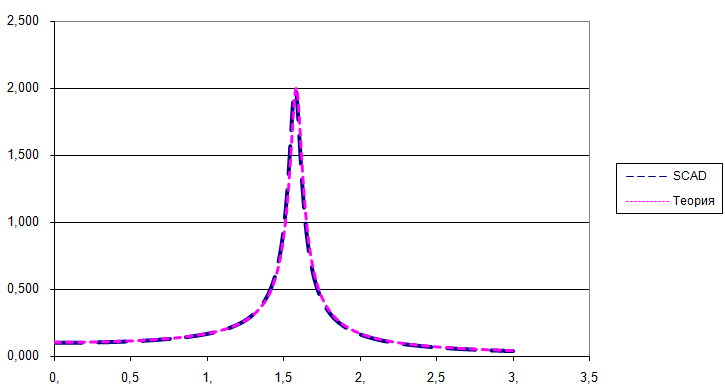
Амплитудно-частотные характеристики

Сравнение решений:

Частота	Перемещение узла
	SCAD	Теория
Гц	м
0,	0,1000	0,1000
0,01	0,1000	0,1000
0,02	0,1000	0,1000
0,03	0,1000	0,1000
0,04	0,1001	0,1001
0,05	0,1001	0,1001
0,06	0,1001	0,1001
0,07	0,1002	0,1002
0,08	0,1003	0,1003
0,09	0,1003	0,1003
0,1	0,1004	0,1004
0,11	0,1005	0,1005
0,12	0,1006	0,1006
0,13	0,1007	0,1007
0,14	0,1008	0,1008
0,15	0,1009	0,1009
0,16	0,1010	0,1010
0,17	0,1012	0,1012
0,18	0,1013	0,1013
0,19	0,1015	0,1015
0,2	0,1016	0,1016
0,21	0,1018	0,1018
0,22	0,1020	0,1020
0,23	0,1022	0,1022
0,24	0,1024	0,1024
0,25	0,1026	0,1026
0,26	0,1028	0,1028
0,27	0,1030	0,1030
0,28	0,1033	0,1032
0,29	0,1035	0,1035
0,3	0,1038	0,1037
0,31	0,1040	0,1040
0,32	0,1043	0,1043
0,33	0,1046	0,1046
0,34	0,1049	0,1048
0,35	0,1052	0,1052
0,36	0,1055	0,1055
0,37	0,1058	0,1058
0,38	0,1062	0,1061
0,39	0,1065	0,1065
0,4	0,1069	0,1068
0,41	0,1072	0,1072
0,42	0,1076	0,1076
0,43	0,1080	0,1080
0,44	0,1084	0,1084
0,45	0,1089	0,1088
0,46	0,1093	0,1092
0,47	0,1097	0,1097
0,48	0,1102	0,1102
0,49	0,1107	0,1106
0,5	0,1112	0,1111
0,51	0,1117	0,1116
0,52	0,1122	0,1121
0,53	0,1127	0,1127
0,54	0,1133	0,1132
0,55	0,1138	0,1138
0,56	0,1144	0,1143
0,57	0,1150	0,1149
0,58	0,1156	0,1155
0,59	0,1163	0,1162
0,6	0,1169	0,1168
0,61	0,1176	0,1175
0,62	0,1183	0,1182
0,63	0,1190	0,1189
0,64	0,1197	0,1196
0,65	0,1204	0,1203
0,66	0,1212	0,1211
0,67	0,1220	0,1219
0,68	0,1228	0,1227
0,69	0,1237	0,1235
0,7	0,1245	0,1244
0,71	0,1254	0,1253
0,72	0,1263	0,1262
0,73	0,1272	0,1271
0,74	0,1282	0,1280
0,75	0,1292	0,1290
0,76	0,1302	0,1300
0,77	0,1313	0,1311
0,78	0,1324	0,1322
0,79	0,1335	0,1333
0,8	0,1346	0,1344
0,81	0,1358	0,1356
0,82	0,1370	0,1368
0,83	0,1383	0,1380
0,84	0,1396	0,1393
0,85	0,1409	0,1406
0,86	0,1423	0,1420
0,87	0,1437	0,1434
0,88	0,1452	0,1449
0,89	0,1467	0,1464
0,9	0,1482	0,1479
0,91	0,1498	0,1495
0,92	0,1515	0,1512
0,93	0,1532	0,1529
0,94	0,1550	0,1546
0,95	0,1569	0,1564
0,96	0,1588	0,1583
0,97	0,1607	0,1603
0,98	0,1628	0,1623
0,99	0,1649	0,1644
1,	0,1671	0,1666
1,01	0,1694	0,1689
1,02	0,1718	0,1712
1,03	0,1742	0,1736
1,04	0,1768	0,1762
1,05	0,1794	0,1788
1,06	0,1822	0,1815
1,07	0,1851	0,1844
1,08	0,1881	0,1873
1,09	0,1912	0,1904
1,1	0,1945	0,1936
1,11	0,1979	0,1970
1,12	0,2014	0,2005
1,13	0,2051	0,2042
1,14	0,2090	0,2080
1,15	0,2131	0,2120
1,16	0,2174	0,2162
1,17	0,2219	0,2207
1,18	0,2266	0,2253
1,19	0,2316	0,2302
1,2	0,2368	0,2354
1,21	0,2424	0,2408
1,22	0,2482	0,2465
1,23	0,2544	0,2526
1,24	0,2609	0,2590
1,25	0,2679	0,2658
1,26	0,2752	0,2731
1,27	0,2831	0,2808
1,28	0,2915	0,2890
1,29	0,3004	0,2977
1,3	0,3100	0,3071
1,31	0,3203	0,3172
1,32	0,3314	0,3280
1,33	0,3434	0,3396
1,34	0,3563	0,3522
1,35	0,3704	0,3659
1,36	0,3857	0,3807
1,37	0,4024	0,3970
1,38	0,4207	0,4147
1,39	0,4409	0,4342
1,4	0,4633	0,4558
1,41	0,4881	0,4797
1,42	0,5159	0,5064
1,43	0,5471	0,5364
1,44	0,5824	0,5702
1,45	0,6226	0,6086
1,46	0,6688	0,6525
1,47	0,7222	0,7032
1,48	0,7845	0,7621
1,49	0,8578	0,8312
1,5	0,9449	0,9130
1,51	1,0490	1,0106
1,52	1,1740	1,1276
1,53	1,3230	1,2675
1,54	1,4965	1,4323
1,55	1,6863	1,6178
1,56	1,8651	1,8048
1,57	1,9824	1,9508
1,58	1,9869	2,0000
1,59	1,8746	1,9270
1,6	1,6930	1,7643
1,61	1,4959	1,5684
1,62	1,3140	1,3792
1,63	1,1575	1,2132
1,64	1,0264	1,0732
1,65	0,9174	0,9565
1,66	0,8265	0,8594
1,67	0,7501	0,7780
1,68	0,6854	0,7092
1,69	0,6301	0,6506
1,7	0,5824	0,6003
1,71	0,5409	0,5566
1,72	0,5045	0,5184
1,73	0,4724	0,4848
1,74	0,4439	0,4550
1,75	0,4184	0,4284
1,76	0,3956	0,4046
1,77	0,3749	0,3831
1,78	0,3561	0,3636
1,79	0,3390	0,3459
1,8	0,3234	0,3297
1,81	0,3091	0,3149
1,82	0,2959	0,3013
1,83	0,2837	0,2887
1,84	0,2724	0,2771
1,85	0,2619	0,2663
1,86	0,2521	0,2562
1,87	0,2430	0,2468
1,88	0,2344	0,2381
1,89	0,2264	0,2299
1,9	0,2189	0,2222
1,91	0,2119	0,2149
1,92	0,2052	0,2081
1,93	0,1989	0,2017
1,94	0,1930	0,1956
1,95	0,1873	0,1898
1,96	0,1820	0,1844
1,97	0,1769	0,1792
1,98	0,1721	0,1743
1,99	0,1675	0,1696
2,	0,1631	0,1651
2,01	0,1590	0,1609
2,02	0,1550	0,1568
2,03	0,1512	0,1529
2,04	0,1475	0,1492
2,05	0,1440	0,1457
2,06	0,1407	0,1423
2,07	0,1375	0,1390
2,08	0,1344	0,1359
2,09	0,1314	0,1329
2,1	0,1286	0,1300
2,11	0,1259	0,1272
2,12	0,1232	0,1245
2,13	0,1207	0,1219
2,14	0,1182	0,1194
2,15	0,1159	0,1170
2,16	0,1136	0,1147
2,17	0,1114	0,1125
2,18	0,1093	0,1103
2,19	0,1072	0,1082
2,2	0,1052	0,1062
2,21	0,1033	0,1043
2,22	0,1014	0,1024
2,23	0,0996	0,1005
2,24	0,0979	0,0988
2,25	0,0962	0,0971
2,26	0,0945	0,0954
2,27	0,0929	0,0938
2,28	0,0914	0,0922
2,29	0,0899	0,0907
2,3	0,0884	0,0892
2,31	0,0870	0,0877
2,32	0,0856	0,0863
2,33	0,0842	0,0850
2,34	0,0829	0,0836
2,35	0,0817	0,0823
2,36	0,0804	0,0811
2,37	0,0792	0,0799
2,38	0,0780	0,0787
2,39	0,0769	0,0775
2,4	0,0757	0,0764
2,41	0,0747	0,0753
2,42	0,0736	0,0742
2,43	0,0725	0,0731
2,44	0,0715	0,0721
2,45	0,0705	0,0711
2,46	0,0696	0,0701
2,47	0,0686	0,0692
2,48	0,0677	0,0682
2,49	0,0668	0,0673
2,5	0,0659	0,0664
2,51	0,0650	0,0655
2,52	0,0642	0,0647
2,53	0,0634	0,0639
2,54	0,0626	0,0630
2,55	0,0618	0,0622
2,56	0,0610	0,0615
2,57	0,0602	0,0607
2,58	0,0595	0,0599
2,59	0,0588	0,0592
2,6	0,0581	0,0585
2,61	0,0574	0,0578
2,62	0,0567	0,0571
2,63	0,0560	0,0564
2,64	0,0553	0,0557
2,65	0,0547	0,0551
2,66	0,0541	0,0545
2,67	0,0535	0,0538
2,68	0,0528	0,0532
2,69	0,0522	0,0526
2,7	0,0517	0,0520
2,71	0,0511	0,0514
2,72	0,0505	0,0509
2,73	0,0500	0,0503
2,74	0,0494	0,0498
2,75	0,0489	0,0492
2,76	0,0484	0,0487
2,77	0,0479	0,0482
2,78	0,0473	0,0477
2,79	0,0469	0,0472
2,8	0,0464	0,0467
2,81	0,0459	0,0462
2,82	0,0454	0,0457
2,83	0,0449	0,0452
2,84	0,0445	0,0448
2,85	0,0440	0,0443
2,86	0,0436	0,0439
2,87	0,0432	0,0435
2,88	0,0427	0,0430
2,89	0,0423	0,0426
2,9	0,0419	0,0422
2,91	0,0415	0,0418
2,92	0,0411	0,0414
2,93	0,0407	0,0410
2,94	0,0403	0,0406
2,95	0,0399	0,0402
2,96	0,0396	0,0398
2,97	0,0392	0,0394
2,98	0,0388	0,0391
2,99	0,0385	0,0387
3,	0,0381	0,0384

	Теория	SCAD	Отклонение
Частота, при которой реализуется максимальное перемещение (Гц)	1.58	1.58	0 %
Максимальное перемещений (м)	2,0000	1,9869	0.65 %

Замечания: При аналитическом решении вертикальное перемещение описывается следующей передаточной функцией

\[ \frac{1}{\sqrt {\left( {1-\frac{\theta^{2}}{\omega^{2}}} \right)^{2}+\left( {2\xi \theta /\omega } \right)^{2}} ,} \]

где ω — собственная частота колебаний недемпфированной системы.