Балка, защемленная по двум торцам, под действием поперечного смещения одного из них

Цель: Определение напряженного состояния балки, защемленной по двум торцам, от воздействия поперечного смещения одного из них.

Файл с исходными данными: CS09_v11.3.spr

Формулировка задачи: Балка прямоугольного поперечного сечения, защемленная по двум торцам, подвергается поперечному смещению v одного из них. Определить поперечную силу Q и изгибающий момент M по смещенному торцу.

Ссылки: J. M. Gere and W. Weaver, Jr., Analysis of Framed Structures, New York, D. Van Nostrand Co., 1965.

Исходные данные:

E = 3.0·107 Па	- модуль упругости,
L = 80.0 м	- длина балки;
b = 2.0 м	- ширина поперечного сечения балки;
h = 2.0 м	- высота поперечного сечения балки;
v = 1.0 м	- значение поперечного смещения.

 

Конечноэлементная модель: Расчетная  схема – плоская рама, 4 элемента типа 2. Сетка конечных элементов разбита по длине продольной оси (вдоль оси X общей системы координат) с шагом 20.0 м. Обеспечение граничных условий на защемленных торцах достигается за счет наложения связей по направлениям степеней свободы: X, Z, UY. Воздействие заданного поперечного смещения задается смещением по оси Z общей системы координат соответствующей связи. Количество узлов в расчетной схеме – 5.

Результаты решения в SCAD

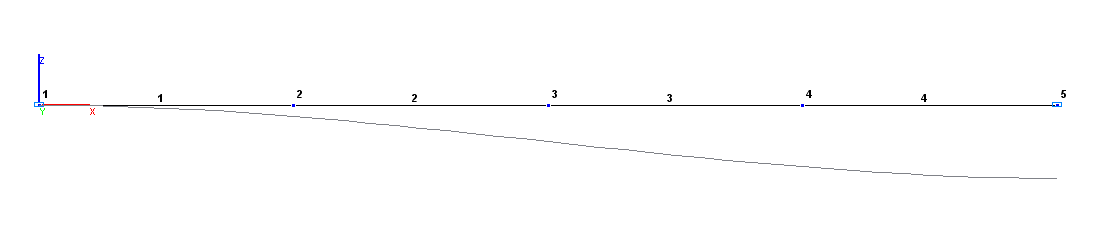
Расчетная и деформированная схемы

Эпюра поперечных сил Q (Н)

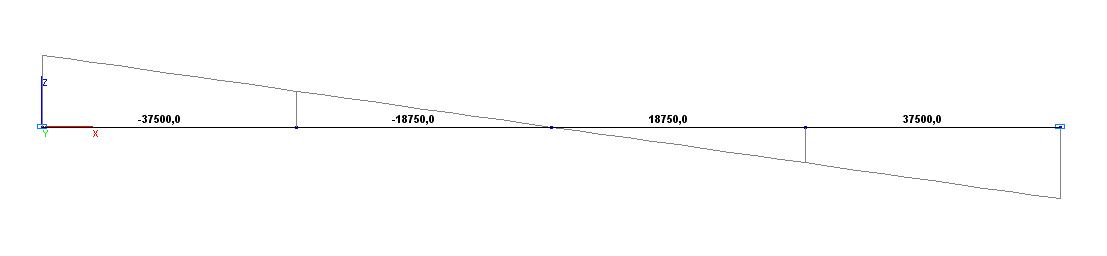
Эпюра изгибающих моментов М (Н•м)

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
Поперечная сила Q по смещенному торцу, Н	937.5	937.5	0.00
Изгибающий момент M по смещенному торцу, Н•м	37500.0	37500.0	0.00

Замечания: При аналитическом решении поперечная сила Q и изгибающий момент M по смещенному торцу определяются по следующим формулам:

\[ Q=\frac{12\cdot E\cdot I}{L^{3}}; \quad M=\frac{6\cdot E\cdot I}{L^{2}}, где: I=\frac{b\cdot h^{3}}{12}. \]