Пример продавливание у края плиты (СП)

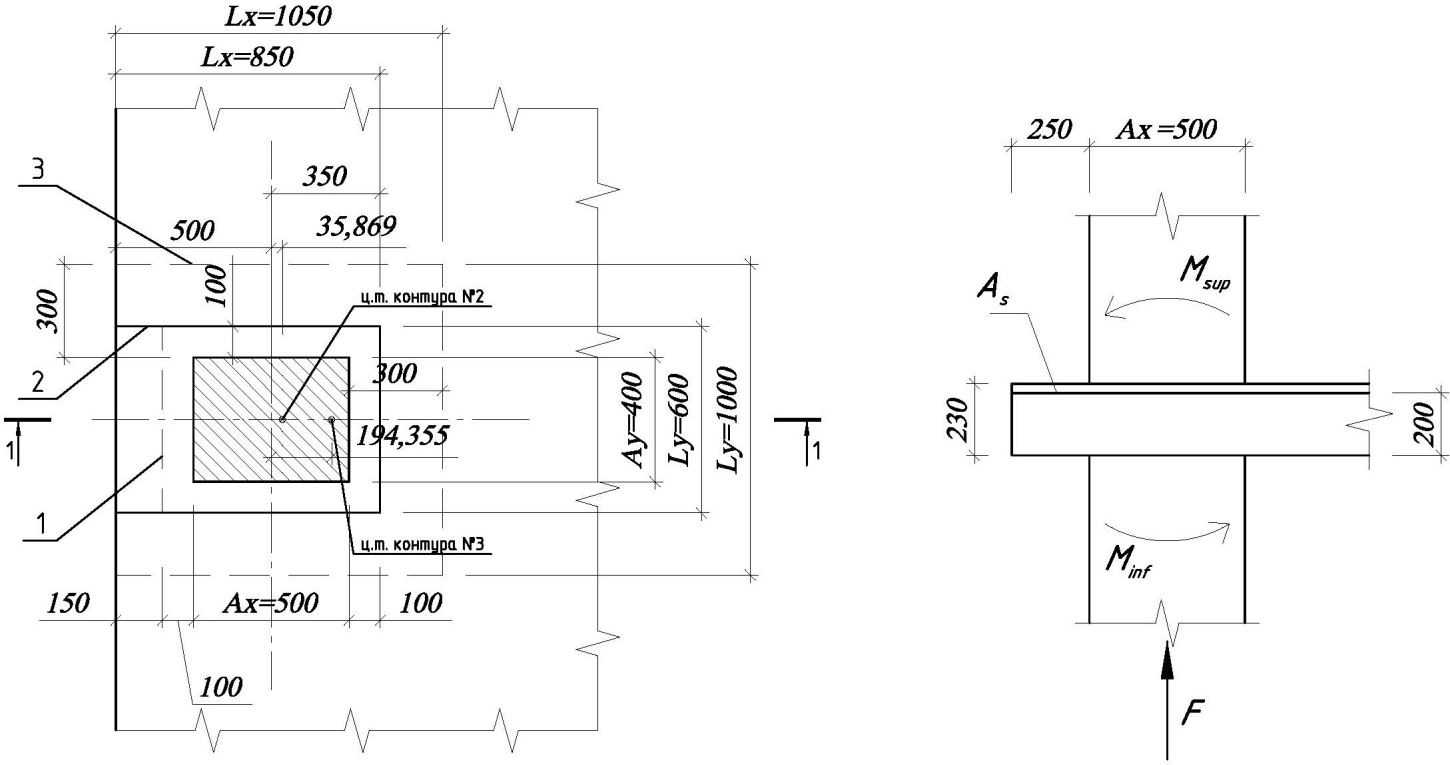
1 – замкнутый расчетный контур №1, 2 – незамкнутый расчетный контур №2, 3 – незамкнутый расчетный контур №3.

Расчет плиты плоского монолитного перекрытия на продавливание

Цель: Проверка режима расчета на продавливание в постпроцессоре «Железобетон» вычислительного комплекса SCAD

Задача: Проверить правильность анализа прочности на продавливание бетонного элемента при действии сосредоточенной силы и изгибающего момента в случае расположения площадки приложения нагрузки у края плиты.

Соответствие нормативам: СНиП 52-101-2003, СП 63.13330.2012.

Файл с исходными данными:
SCAD 41 SP-2003.spr,
SCAD 41 SP-2012.spr 
отчет – SCAD 41 SP-2003.doc
отчет – SCAD 41 SP-2012.doc

Исходные данные:

h = 230 мм	Толщина плиты
h0 = 200 мм	Усреднённая рабочая высота плиты
a×b = 500×400 мм	Размеры сечения колонн
F = 150 кН	Нагрузка, передающаяся с перекрытия на колонну
Msup = 80 кН∙м	Момент в сечении колонны по верхней грани плиты
Minf = 90 кН∙м	Момент в сечении колонны по нижней грани плиты
x0 = 500 мм	Расстояние от центра сечения колонны до свободного края плиты
Класс бетона	В25

Аналитическое решение:

В данном случае необходимо проверить прочность трех контуров расчетного поперечного сечения:Аналитическое решение:

контур №1 – замкнутый контур вокруг сечения колонны на расстоянии 0,5h₀ от контура колонны;

контур №2 – незамкнутый контур вокруг сечения колонны на расстоянии 0,5h₀ от контура колонны с продлением контура до свободного края плиты;

контур №3 – незамкнутый контур вокруг сечения колонны на расстоянии 1,5h₀ от контура колонны (контура поверочного расчета без учета арматуры).

1. Замкнутый контур №1:

L_x = A_x + h₀ = 500 + 200 = 700 mm = 0,7 m,

L_y = A_y + h₀ = 400 + 200 = 600 mm = 0,6 m,

Периметр расчетного контура поперечного сечения:

u = 2(L_x + L_y) = 2 (0,7 + 0,6) = 2,6 m.

Площадь расчетного контура поперечного сечения:

A_b = uh₀ = 2,6 х 0,2 = 0,52 m².

Предельное усилие, воспринимаемое бетоном:

F_b,ult = R_btA_b = 1,05 х10³ х 0,52 = 546 кН.

Момент инерции расчетного контура относительно оси Х, проходящей через его центр тяжести:

\[
I_{bx} =2\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}=
\quad
2\frac{0,6^{3} }{12}+2\cdot 0,7\left( {\frac{0,6}{2}} \right)^{2}=\quad 
0,162 м^{3}.
\]

Момент сопротивления расчетного контура бетона

\[
W_{bx} =\frac{I_{bx} }{y_{\max } }==
\quad
\frac{0,162}{0,3}=\quad 0,54  м^{2}.
\]

Момент инерции расчетного контура относительно оси Y, проходящей через его центр тяжести:\[
I_{by} =2\frac{L_{x}^{3} }{12}+2\cdot L_{y} \left( {\frac{L_{x} }{2}} 
\right)^{2}=
\quad
2\frac{0,7^{3} }{12}+2\cdot 0,6\left( {\frac{0,7}{2}} \right)^{2}=\quad 
0,204 м^{3}.
\]

Момент сопротивления расчетного контура бетона

\[
W_{by} =\frac{I_{by} }{x_{\max } }==
\quad
\frac{0,204}{0,35}=\quad 0,583 м^{2}.
\]

Изгибающий момент, который может быть воспринят бетоном в расчетном поперечном сечении:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 1,217 х 0,2 = 255,57 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,547 х 0,2 = 114,87 кНм.

M_y = M_y - Fe₀ = 85 – 150х0,194355 = 85 – 29,15 = 55,85 кНм.

Для СНиП 52-101-2003:

\[
\frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} };
\quad
\frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} }
\]
\(
\frac{M_{y} }{M_{by,ult} }=\frac{55,85}{114,87}=0,486\le \frac{F}{F_{b,ult} 
}=\frac{150}{651}=0,23 \)- условие не выполняется.

Принимаем

\[
\frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,275
\]

Прочность плиты при продавливании:

\[
K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} 
}+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0
\]

\[
К1 = 0,275 + 0 + 0,275 = 0,55
\]

Для СП 63.13330.2012:

\[
\frac{M_{x} }{M_{bx,ult} } + \frac{M_{y} }{M_{by,ult} } \le 0,5 \frac{F}{F_{b,ult} } 
\]

\( \frac{M_{y} }{M_{by,ult} }=\frac{85}{122,4}=0,694\le 0,5\frac{F}{F_{b,ult} 
}=\frac{150}{546}=0,5\cdot 0,275=0,1375\quad \) – условие не выполняется.

Принимаем

\[
\frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,1375
\]

Прочность плиты при продавливании:

\[
K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} 
}+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0
\]

\[
К1 = 0,275 + 0 + 0,1375 = 0,413
\]

Незамкнутый контур №2:

L_x =A_x +h₀ + 150 = 500 + 200 + 150 = 850 мм = 0,85 м,

L_y =A_y +h₀ = 400 + 200 = 600 мм = 0,6 м,

Периметр расчетного контура поперечного сечения:

u = 2L_x + L_y = 2х0,85 + 0,6 = 2,3 м.

Площадь расчетного контура поперечного сечения:

_Ab = uh₀ = 2,3 х 0,2 = 0,46 м².

Координата Х центра тяжести незамкнутого контура относительно левого края плиты:

\[
X=\frac{425\cdot 850\cdot 2+850\cdot 600}{850\cdot 2+600}=535,869 мм
\]

Предельное усилие, воспринимаемое бетоном:

F_b,ult = R_btA_b = 1,05 х10³ х 0,46 = 483 кН.

Момент инерции расчетного контура относительно оси Х, проходящей через его центр тяжести:

\[
I_{bx} =\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}=
\quad
\frac{0,6^{3} }{12}+2\cdot 0,85\left( {\frac{0,6}{2}} \right)^{2}=\quad 
0,171 м^{3}.
\]

Момент сопротивления расчетного контура бетона

\[
W_{bx} =\frac{I_{bx} }{y_{\max } }=
\quad
\frac{0,171}{0,3}=\quad 0,57 м^{2}.
\]

Момент инерции расчетного контура относительно оси Y, проходящей через его центр тяжести:

\[
I_{by} =2\frac{L_{x}^{3} }{12}+2L_{x} (0,075+0,035869)^{2}+L_{y} \left( 
{0,35-0,035869} \right)^{2}=
2\frac{0,85^{3} }{12}+2\cdot 0,85(0,075+0,035869)^{2}+0,6\left( 
{0,35-0,035869} \right)^{2}=0,183 м^{3}.
\]

Момент сопротивления расчетного контура бетона

\[
W_{by} =\frac{I_{by} }{x_{\max } }=
\quad
\frac{0,183}{0,535869}=\quad 0,341 м^{2}.
\]

Изгибающий момент, который может быть воспринят бетоном в расчетном поперечном сечении:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 0,57 х 0,2 = 119,7 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,341 х 0,2 = 71,6 кНм.

M_y = M_y - Fe₀ = 85 – 150х0,035869 = 85 – 5,38 = 79,62 кНм.

Для СНиП 52-101-2003:

\[
\frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} };
\quad
\frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} }
\]

\( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le \frac{F}{F_{b,ult} 
}=\frac{150}{483}=0,311 \)  – условие не выполняется.

Принимаем

\[
\frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,311
\]

Прочность плиты при продавливании:

\[
K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} 
}+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0
\]
\[
К1 = 0,311+0+0,311 = 0,622
\]

 

Для СП 63.13330.2012:

\[
\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 
0,5\frac{F}{F_{b,ult} }
\]
\( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le 0,5\frac{F}{F_{b,ult} 
}=\frac{150}{483}=0,5\cdot 0,311=0,155 \) – условие не выполняется.

Принимаем

\[
\frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,155
\]

Прочность плиты при продавливании:

\[
K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} 
}+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0
\]
\[
К1 = 0,311 + 0 + 0,155 = 0,466
\]

Незамкнутый контур №3:

L_x = A_x + 1,5h₀ + 250 = 500 +1,5х200 + 250 = 1050 мм = 1,05 м,

L_y = A_y + 2·1,5h₀ = 400 + 2х1,5х200 = 1000 мм = 1,0 м,

Периметр расчетного контура поперечного сечения:

u = 2L_x + L_y = 2х1,05 + 1,0 = 3,1 м.

Площадь расчетного контура поперечного сечения:

A_b = uh₀ = 3,1 х 0,2 = 0,62 м².

Координата Х центра тяжести незамкнутого контура относительно левого края плиты:

\[
X=\frac{525\cdot 1050\cdot 2+1050\cdot 1000}{1050\cdot 2+1000}=694,355 мм
\]

Предельное усилие, воспринимаемое бетоном:

F_b,ult = R_btA_b = 1,05 х10³ х 0,62 = 651 кН.

Момент инерции расчетного контура относительно оси Х, проходящей через его центр тяжести:

\[
I_{bx} =\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}=
\quad
\frac{1,05^{3} }{12}+2\cdot 1,05\left( {\frac{1,0}{2}} \right)^{2}=\quad 
0,608 м^{3}.
\]

Момент сопротивления расчетного контура бетона

\[
W_{bx} =\frac{I_{bx} }{y_{\max } }=
\quad
\frac{0,608}{0,5}=\quad 1,217 м^{2}.
\]

Момент инерции расчетного контура относительно оси Y, проходящей через его центр тяжести:

\[
I_{by} =2\frac{L_{x}^{3} }{12}+2L_{x} (0,194355-0,025)^{2}+L_{y} \left( 
{1,05-0,694355} \right)^{2}=
2\frac{1,05^{3} }{12}+2\cdot 1,05(0,194355-0,025)^{2}+1,0\left( 
{1,05-0,694355} \right)^{2}=0,38 м^{3}.
\]

Момент сопротивления расчетного контура бетона

\[
W_{by} =\frac{I_{by} }{x_{\max } }=
\quad
\frac{0,38}{0,694355}=\quad 0,547 м^{2}.
\]

Изгибающий момент, который может быть воспринят бетоном в расчетном поперечном сечении:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 1,217 х 0,2 = 255,57 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,547 х 0,2 = 114,87 кНм.

M_y = M_y - Fe₀ = 85 – 150х0,194355 = 85 – 29,15 = 55,85 кНм.

Для СНиП 52-101-2003:

\[
\frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} };
\quad
\frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} }
\]

\( \frac{M_{y} }{M_{by,ult} }=\frac{55,85}{114,87}=0,486\le \frac{F}{F_{b,ult} 
}=\frac{150}{651}=0,23 \) – условие не выполняется.

Принимаем

\[
\frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,23
\]

Прочность плиты при продавливании:

\[
K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} 
}+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0
\]
\[
К1 = 0,23 + 0 + 0,23 = 0,46
\]

Для СП 63.13330.2012:

\[
\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 
0,5\frac{F}{F_{b,ult} }
\]

\( \frac{M_{y} }{M_{by,ult} }=\frac{55,85}{114,87}=0,486\le 
0,5\frac{F}{F_{b,ult} }=\frac{150}{651}=0,5\cdot 0,23=0,115 \)  – условие не выполняется.

Принимаем

\[
\frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,155
\]

Прочность плиты при продавливании:

\[
K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} 
}+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0
\]
\[
К1 = 0,23 + 0 + 0,115 = 0,345
\]

Результаты расчета SCAD:

Узел № 5

Коэффициент надежности по ответственности γ_n = 1
Бетон
Вид бетона: Тяжелый
Класс бетона: B25

Коэффициенты условий работы бетона
γb1	учет нагрузок длительного действия	1
γb2	учет характера разрушения	1
γb3	учет вертикального положения при бетонировании	1
γb4	учет замораживания/оттаивания и отрицательных температур	1

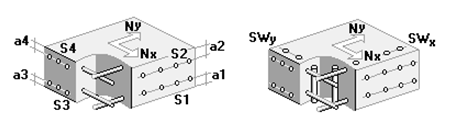
Расстояние до ц.т. арматуры
a1	a2	a3	a4
мм	мм	мм	мм
30	30	0	0

Результаты расчета
Расчетный случай – крайняя колонна
Длина контура верхнего основания пирамиды продавливания - 1800 мм
Длина контура нижнего основания пирамиды продавливания - 2300 мм

Сравнение решений (по СНиП 52-101-2003)

Проверено по СНиП	Проверка	Коэффициент использования
п.6.2.49	Прочность без учета армирования	0,62

Проверка	прочность на продавливание по незамкнутому контуру бетонного элемента при действии сосредоточенной силы и изгибающих моментов (в том числе дополнительных от внецентренного приложения силы относительно контура продавливания) с векторами вдоль осей X,Y (площадка приложения у края плиты)
Аналитическое решение	0,622
SCAD	0,62
Отклонение, %	0,1 %

Сравнение решений (по СП 63.13330.2012)

Проверено по СП	Проверка	Коэффициент использования
п.8.1.49	Прочность без учета армирования	0,47

Проверка	прочность на продавливание по незамкнутому контуру бетонного элемента при действии сосредоточенной силы и изгибающих моментов (в том числе дополнительных от внецентренного приложения силы относительно контура продавливания) с векторами вдоль осей X,Y (площадка приложения у края плиты)
Аналитическое решение	0,466
SCAD	0,47
Отклонение, %	0,1 %