Неоднородное демпфирование. Возврат в положение статического равновесия

Цель: проверка того, что под воздействием кратковременных нагрузок и при наличии затухания механическая система после того, как нагрузка перестала изменяться во времени (назовем эту величину статической составляющей нагрузки), должна вернуться в положение статического равновесия, соответствующего статической составляющей нагрузки.

Консольно-защемленная балка с локальным демпфером

Имя файлов с исходными данными:
beam_local_damp_1.SPR - расчетная схема
FileTimeFile.txt - функция времени

Формулировка задачи:

Рассматривается консольно-защемленная балка длиной a = 3 м с прямоугольным поперечным сечением 0.2 × 0.5 м и модулем упругости E = 23053.5 МН/м². Объемный вес равен γ = 0.0245 МН/м³. Балка поделена на 3 конечных элемента. Используется матрица сосредоточенных масс. Максимальное значение силы P составляет 0.01 МН.

Зависимость нагрузки от времени приведена на рисунке:

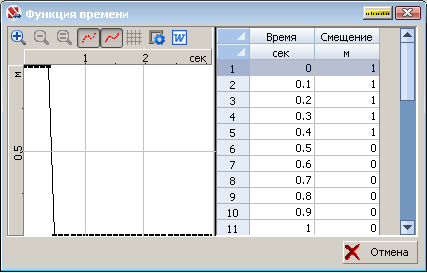
Конечноэлементная модель: Расчетная  схема – система общего вида, 6 стержневых элементов общего вида (тип 5) и один одноузловой демпфер (тип 56). Количество узлов в расчетной схеме – 8. При расчете используется матрица сосредоточенных масс.

Результаты решения в SCAD

На рисунке представлена зависимость вертикального перемещения края консоли от времени при c = 0.01 МН∙с/м.

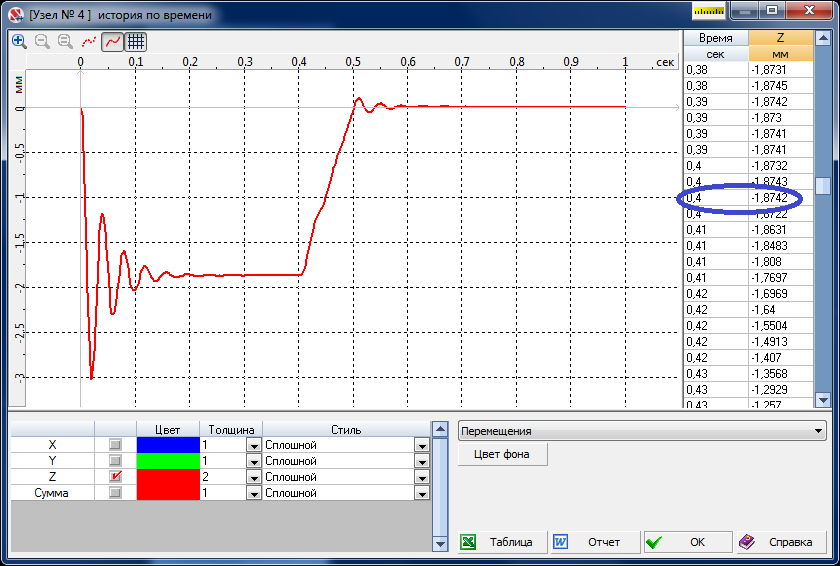
Вертикальное перемещение края консоли

Учитывается только демпфирование, обусловленное наличием локального демпфера. При внезапном приложении нагрузки возникают поперечные колебания балки, которые быстро затухают. На рисунке обведено значение прогиба, соответствующего состоянию статического равновесия при величине силы равной 0.01 МН. Точное решение соответствующей задачи статики равно w_st = Pa³/(3EI) = – 0.0018739 м. При решении задачи динамики методом Ньюмарка шаг интегрирования принимался равным 0.001 с. При этом верными получаются 3 значащих цифры. Это позволяет утверждать, что после затухания колебаний мы выходим на статическое решение данной задачи. При 0.4 с < t ≤ с 0.5 происходит уменьшение нагрузки до нуля. Снова возникают колебания, которые быстро затухают. При t = 1 c величина нормального прогиба равна w = –1.533∙10^–7 м, что по сравнению с максимальным по абсолютной величине прогибом w_max = – 3.024∙10^–3 м является хорошим приближением нуля – точного значения статического прогиба при отсутствии нагрузки.

Таким образом, численное решение, полученное методом Ньюмарка, после затухания колебаний сходится к статическому решению данной задачи, что подтверждает достоверность полученных результатов.