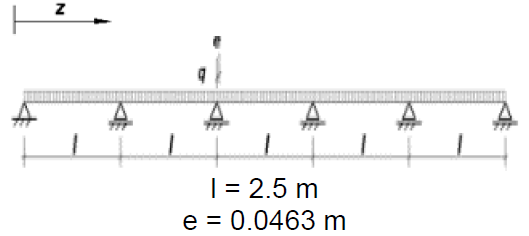
Определение внутренних усилий при стесненном кручении тонкостенных стержней открытого профиля

Цель: Проверить правильность определения значений внутренних усилий при стесненном кручении тонкостенного стержня открытого профиля на примере пятипролетной балки.

Формулировка задачи: пятипролетная балка с равными пролетами величиной 2,5 м нагружена поперечной равномерно-распределенной нагрузкой 20 кН/м, ориентированной в плоскости стенки. Поперечное сечение балки принято из С-образного тонкостенного холодногнутого профиля. Нагрузка приложена по верхней полке балки в плоскости стенки с эксцентриситетом по отношению к центру масс равным 46.3 мм. Определить значения бимоментов в сечениях балки.

Источник: A.D. Pavlenko, V.A. Rybakov, A.V. Pikht, E.S. Mikhailov. Non-uniform torsion of thin-walled open-section multi-span beams // Magazine of Civil Engineering, No. 7(67), 2016, pp. 55-69.

Имя файла с исходными данными:
Rybakov_5SpanBeam.spr;

Версия программ:

SCAD++ 23.1.1.3

Исходные данные задачи:

Е = 210000 Н/мм²	Модуль упругости
v = 0.3	Коэффициент Пуассона
Тип сечения	Швеллер
h = 220 мм	Высота сечения (по внешней грани)
b = 70 мм	Ширина полки (по внешней грани)
t = 2 мм	Толщина профиля (за минусом толщины покрытия)
q = 20 кН/м	Равномерно-распределенная нагрузка на балку
l = 2.5 м	Длина каждого пролета балки
е = 46.3 мм	Эксцентриситет приложенной нагрузки (нагрузка приложена по верхней полке профиля, посередине полки)

Конечно-элементная модель: расчетная схема многопролетной балки – пространственная стержневая система. Ось балки совмещена с направлением оси x – x глобальной системы координат. На крайней левой опоре заданы ограничения на поворот относительно оси x – x, а также линейные перемещения в направлении y – y и z – z осей глобальной системы координат. На промежуточных опорах заданы ограничения на линейные перемещения в направлении осей y – y и z – z.

Принимая во внимание конструктивное решение стыков многопролетной балки внахлест, на промежуточных опорах задавалось условие равенства депланаций. Кроме того, это же условие задавалось во всех промежуточных узлах балки. На крайних опорах балки условие равенства нулю бимомента реализовывалось введением шарнира по депланациям.

Эксцентриситет приложения равномерно-распределенной нагрузки на балку учтен путем приложения равномерно-распределенного крутящего момента величиной М = q×е = 20 кН/м × 46.3 мм = 0,926 кНм/м.

Результаты программы SCAD++:

Результирующая эпюра бимоментов, вычисленная в SCAD++, представлена на рис. 1.

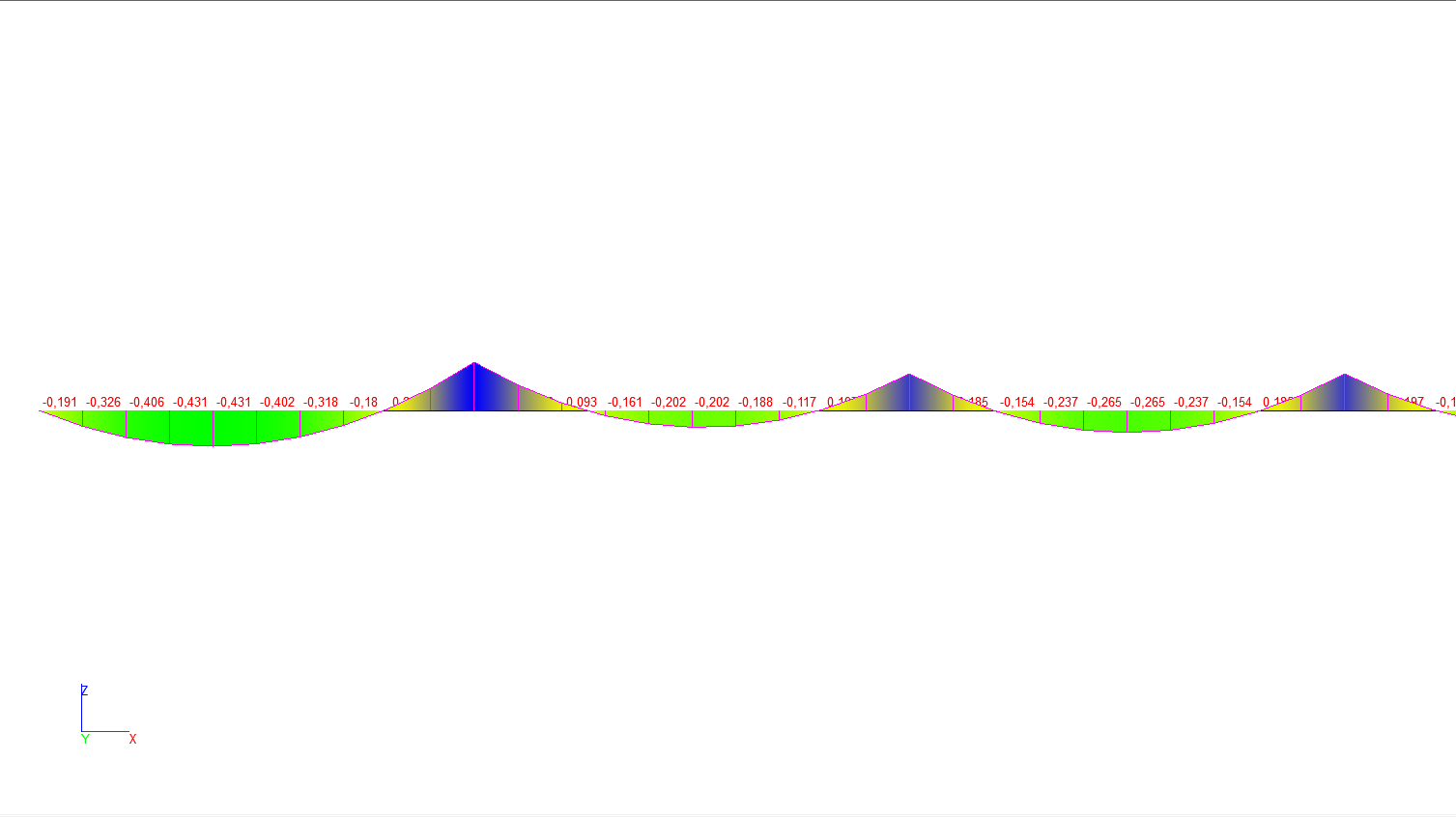
Рис. 1. Эпюра бимоментов при стесненном кручении пятипролетной балки с пролетами 2,5 м.

Сравнение решений

Расчетная схема балки	Расположение сечения балки
	z = 1 м	z = 1,25 м	z = 2,5 м	z = 3,75 м	z = 5,0 м	z = 6,25 м
Бимомент (аналитическое решение), кНм²	0,43	0,39	–0,59	0,19	–0,45	0,25
Бимомент в SCAD++, кНм²	0,4253	0,395	–0,5958	0,1908	–0,4533	0,2551
Отклонение, %	1,1	1,3	0,99	0,42	0,73	2,0