Система перекрестных стержней под действием распределенной нагрузки и сосредоточенной силы в их плоскости
Цель: Определение напряженно-деформированного состояния системы перекрестных стержней от воздействия распределенной нагрузки и сосредоточенной силы в их плоскости.
Файл с исходными данными: SSLL10_v11.3.spr
Формулировка задачи: Система состоит из двух перекрестных стержней квадратного поперечного сечения, горизонтального (BD) и вертикального (CE) , жестко соединенных в общем узле (точка А). Горизонтальный стержень жестко защемлен в левом и правом узлах (точки D и B). Вертикальный стержень жестко защемлен в нижнем узле (точка E) и шарнирно оперт в верхнем узле (точка C). В середине левого пролета горизонтального стержня (точка G) приложена вертикальная сосредоточенная сила F, на правом пролете горизонтального стержня (AB) расположена вертикальная равномерно распределенная нагрузка p. Определить в общем узле перекрестных стержней (точка А) угол поворота UY и изгибающие моменты M в стержнях с обеих сторон от узла.
Ссылки: S. Timoshenko et D.H. Young, Theorie des constructions, Paris, Librairie Polytechnique Beranger, 1949, p. 412-416.
Исходные данные:
| E = 2.0·1011 Па | - модуль упругости стержней системы; |
| LAD = 1.0 м | - длина левого пролета горизонтального стержня; |
| bAD = 1.0 м | - сторона поперечного сечения левого пролета горизонтального стержня; |
| LAB = 4.0 м | - длина правого пролета горизонтального стержня; |
| bAB = 4.0 м | - сторона поперечного сечения правого пролета горизонтального стержня; |
| LAC = 1.0 м | - длина верхнего участка вертикального стержня; |
| bAC = 1.0 м | - сторона поперечного сечения верхнего участка вертикального стержня; |
| LAE = 2.0 м | - длина нижнего участка вертикального стержня; |
| bAE = 2.0 м | - сторона поперечного сечения нижнего участка вертикального стержня; |
| F = 1.0·105 Н | - значение вертикальной сосредоточенной силы; |
| p = 1.0·103 Н/м | - значение вертикальной равномерно распределенной нагрузки. |
Конечноэлементная модель: Расчетная схема – плоская рама, 5 стержневых элемента типа 10. Обеспечение граничных условий достигается за счет наложения связей: по направлениям степеней свободы X, Z для шарнирно опертого узла (точка C) и по направлениям степеней свободы X, Z, UY для жестко защемленных узлов (точки E, D, B). Количество узлов в расчетной схеме – 6.
Результаты решения в SCAD
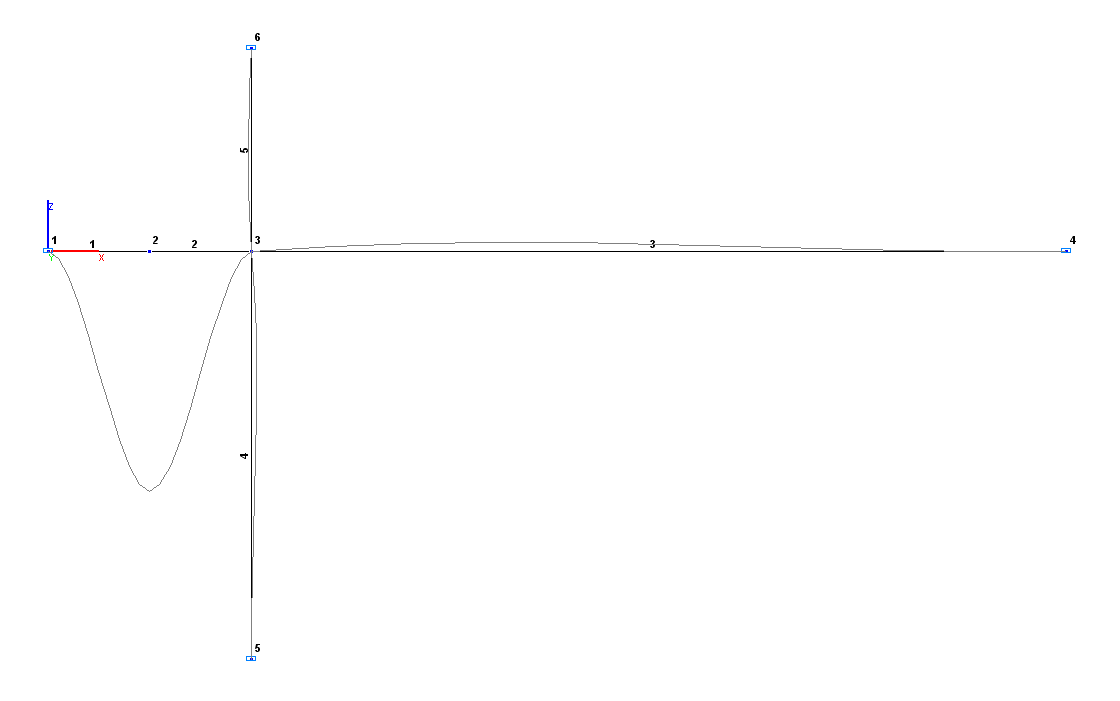
Расчетная и деформированная схемы

Значения углов поворота UY (рад)
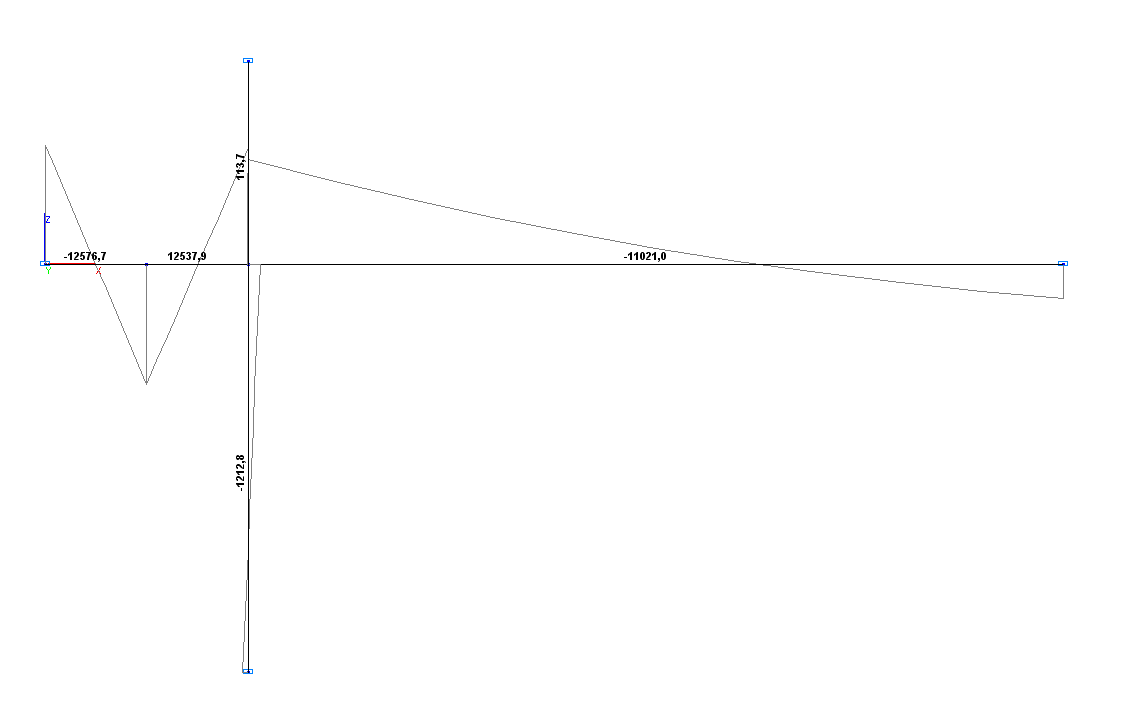
Значения изгибающих моментов M (Н∙м)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Угол поворота UY (точка A), рад |
-2.2712·10-1 |
-2.2740·10-1 |
0.12 |
|
Изгибающий момент M (стержень AD), Н∙м |
-12348.6 |
-12347.5 |
0.01 |
|
Изгибающий момент M (стержень AB), Н∙м |
-11023.7 |
-11021.0 |
0.02 |
|
Изгибающий момент M (стержень AC), Н∙м |
113.6 |
113.7 |
0.09 |
|
Изгибающий момент M (стержень AE), Н∙м |
-1211.3 |
-1212.8 |
0.12 |
