Однопролетная шарнирно опертая плоская рама с двухскатным ригелем под действием вертикальной равномерно распределенной нагрузки, сосредоточенных вертикальных и горизонтальных сил и изгибающего момента

Цель: Определение напряженно-деформированного состояния однопролетной шарнирно опертой плоской рамы с двухскатным ригелем от воздействия вертикальной равномерно распределенной нагрузки, сосредоточенных вертикальных и горизонтальных сил и изгибающего момента.

Файл с исходными данными: SSLL14_v11.3.spr

Формулировка задачи: Однопролетная шарнирно опертая рама с жестким креплением двухскатного ригеля к стойкам находится под воздействием вертикальной равномерно распределенной нагрузки P_zx на длине левого полупролета ригеля 0.5∙L, сосредоточенной вертикальной силы F1 в коньковом узле ригеля (точка C), сосредоточенными горизонтальной силы F2 и изгибающего момента M в узле крепления ригеля к левой стойке. Определить вертикальное перемещение Z в коньковом узле ригеля (точка C), продольную N и поперечную Q силу в опорном узле левой стойки (точка A).

Ссылки: J.C. Bianchi, Rapport de la SOCOTEC, Paris, non publie, 1964.

Исходные данные:

Материал:
E = 2.1∙1011 Па	- модуль упругости;
Стойки L1:
h = 8.0 м	- высота;
EA1 = 1.0∙1010 Н	- продольная жесткость;
EI1 = 2.1∙1011 ∙ 5.0∙10-4 =  10.5∙107 Н∙м2	- изгибная жесткость;
Ригель L2:
L = 20.0 м	- длина пролета;
a = 4.0 м	- высота подъема;
b = ((0.5∙20.0)2 + 4.02)0.5	- длина ската;
EA2 = 1.0∙1010 Н	- продольная жесткость;
EI2 = 2.1∙1011∙2.5∙10-4 =  5.25∙107 Н∙м2	- изгибная жесткость;
Нагрузки и воздействия:
Pzx = 3.0∙103 Н/м	- вертикальная равномерно-распределенная нагрузка на  длине левого полупролета ригеля 0.5∙L;
Pz = 3.0∙103∙0.5∙20.0/((0.5∙20.0)2 + 4.02)0.5 = 2.78543∙103 Н/м	- та же нагрузка на длине левого ската ригеля b;
F1 = 2.0∙104 Н	- сосредоточенная вертикальная сила в коньковом узле ригеля;
F2 = 1.0∙104 Н	- сосредоточенная горизонтальная сила в узле крепления ригеля к левой стойке;
M = 1.0∙105 Н∙м	- сосредоточенный изгибающий момент в узле крепления ригеля к левой стойке.

 

Конечноэлементная модель: Расчетная  схема – плоская рама, ригель – 2 элемента типа 2, стойки – 2 элемента типа 2. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы X, Z для шарнирных опорных узлов. Количество узлов в расчетной схеме – 5.

 

Результаты решения в SCAD

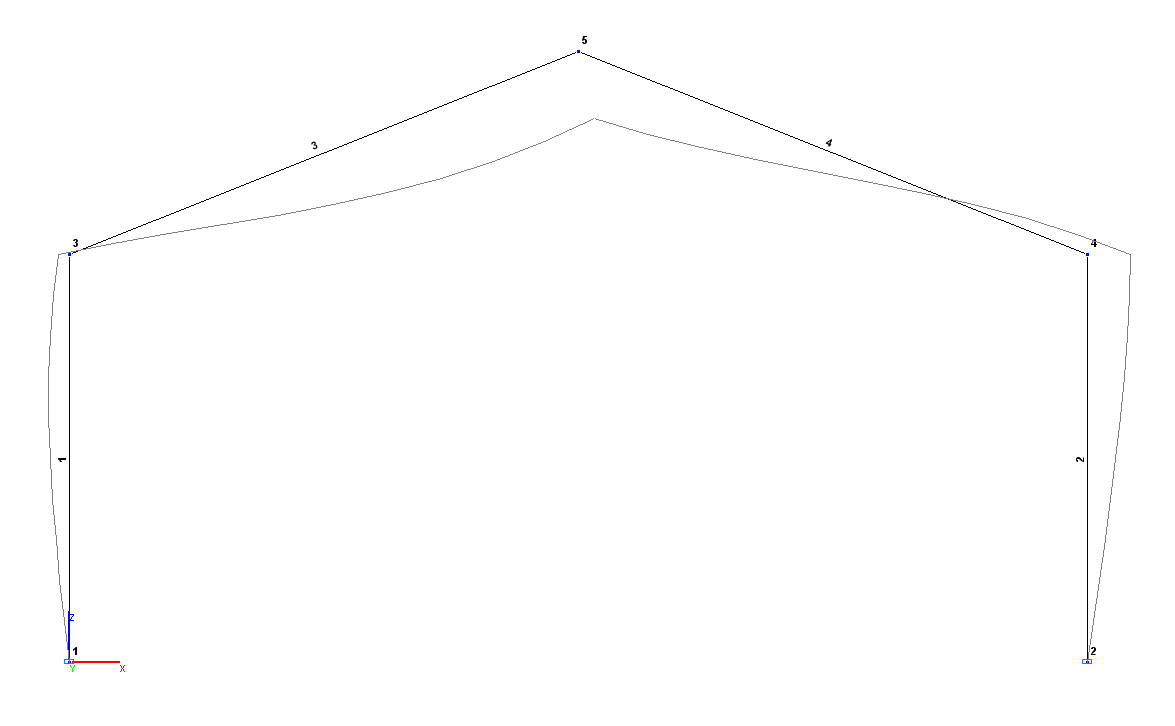
Расчетная и деформированная схемы

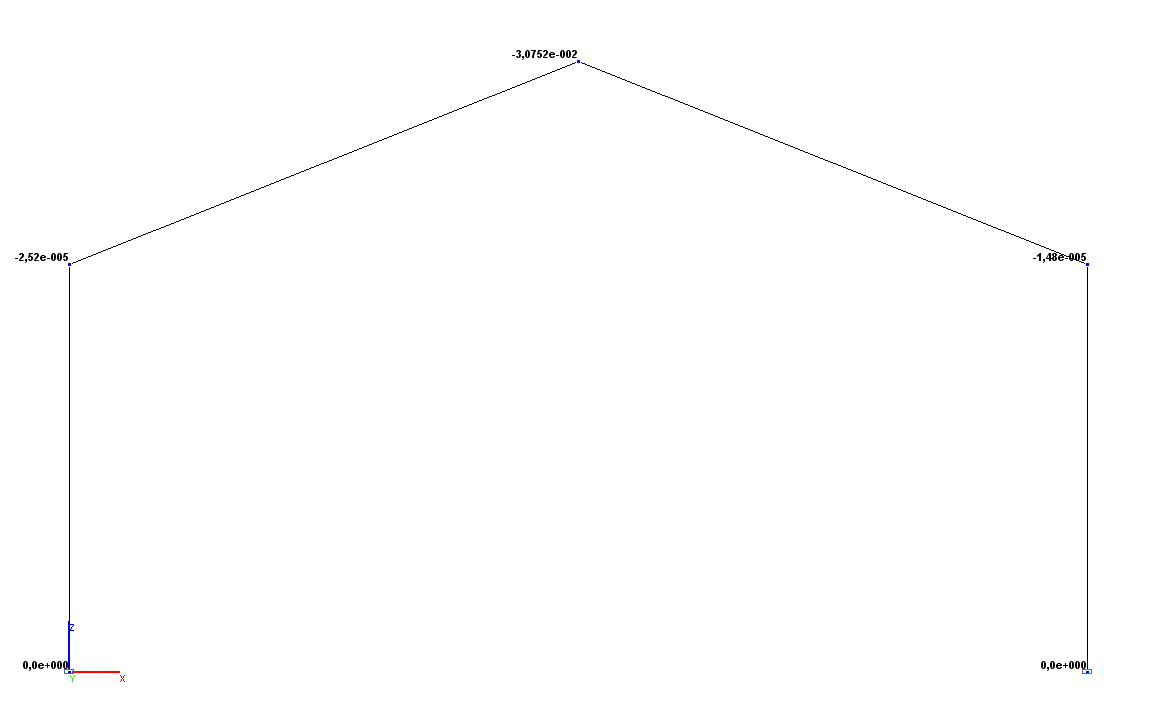
Значения вертикальных перемещений Z (м)

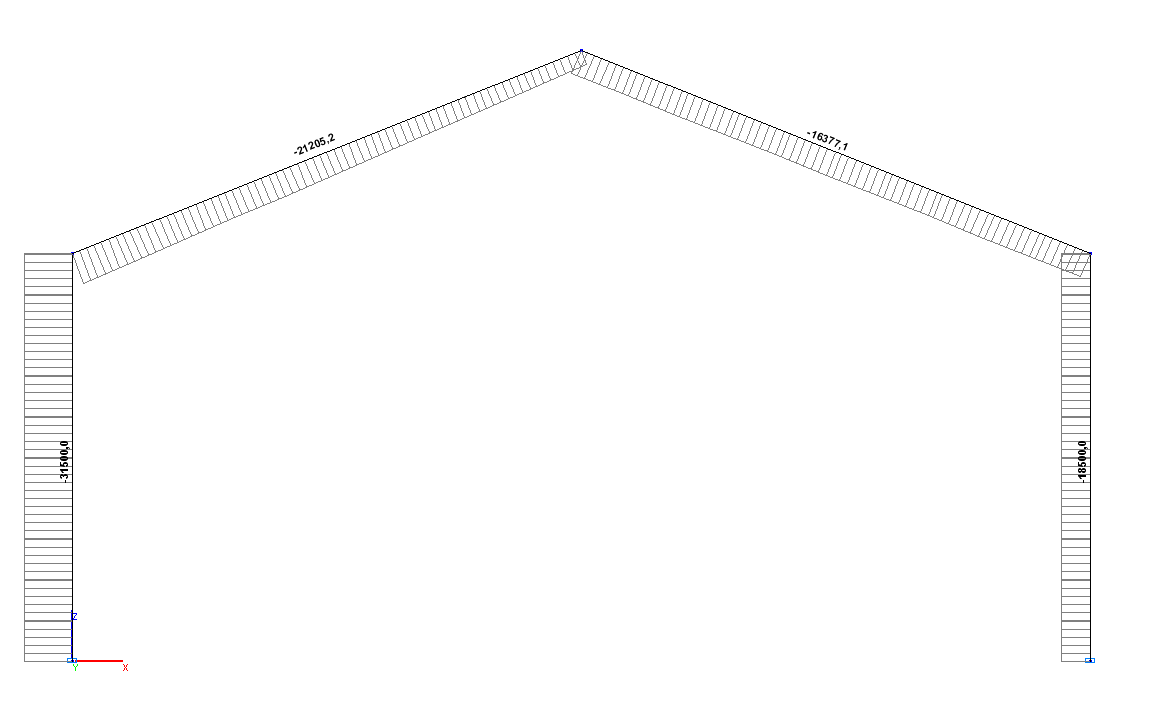
Значения продольных сил N (Н)

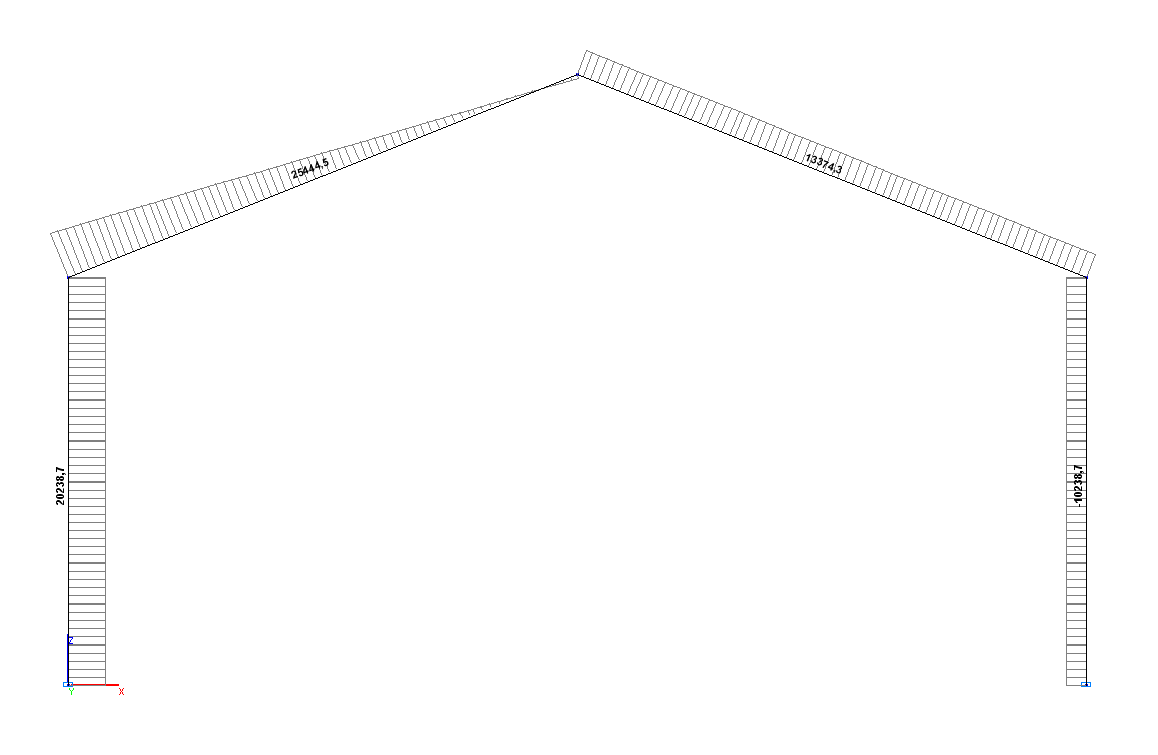
Значения поперечных сил Q (Н)

 

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
Вертикальное перемещение ZC, м	-3.0720∙10-2	-3.0752∙10-2	0.10
Продольное усилие NA, Н	-31.500	-31.500	0.00
Поперечное усилие NA, Н	20239.4	20238.7	0.00