Пространственная стержневая система с упругими связями под действием сосредоточенной силы
Цель: Определение напряженно-деформированного состояния пространственной стержневой системы с упругими связями под действием сосредоточенной силы.
Файл с исходными данными: SSLL04_v11.3.spr
Формулировка задачи: Пространственная система состоит из четырех последовательно соединенных стержней. Крайние стержни ортогонально лежат в параллельных горизонтальных плоскостях, промежуточные стержни являются вертикальными и шарнирно сопрягаются между собой по угловым степеням свободы (точка 3). По обоим концам пространственной системы (точки 1, 5) установлены жесткие связи по линейным и угловой степеням свободы в плоскости поперечного сечения соответствующего крайнего стержня и упругие связи по линейному и угловым степеням свободы из плоскости поперечного сечения соответствующего крайнего стержня. В узле сопряжения верхнего горизонтального и вертикального стержней (точка 4) приложена вертикальная сосредоточенная сила F. Определить вертикальное перемещение Z для узла сопряжения вертикальных стержней (точка 3), горизонтальное перемещение Y вдоль верхнего крайнего стержня и угол поворота UX в вертикальной плоскости, содержащей этот стержень, для верхнего узла закрепления пространственной системы (точка 5), а также крутящий и изгибающие моменты Mx, My, Mz для верхнего и нижнего узлов закрепления пространственной системы (точки 1, 5).
Ссылки: M. Laredo, Resistance des materiaux, Paris, Dunod, 1970, p. 165.
Исходные данные:
| E = 2.1·1011 Па | - модуль упругости, |
| G = 0.7875·1011 Па | - модуль сдвига, |
| l = 2.0 м | - длина горизонтальных стержней; |
| 0.5 l = 1.0 м | - длина вертикальных стержней; |
| A = 1.0·10-3 м2 | - площадь поперечного сечения стержней; |
| Ix = 2·10-6 м4 | - момент инерции в плоскости поперечного сечения стержней (кручения); |
| Iy = Iz = 2·10-6 м4 | - моменты инерции из плоскости поперечного сечения стержней (изгиба); |
| k = 5.25·104 Н/м | - жесткость связей по линейной степени свободы; |
| ku = 5.25·104 Н•м/рад | - жесткость связей по угловым степеням свободы; |
| F = 1.0·104 Н | - значение вертикальной сосредоточенной силы. |
Конечноэлементная модель: Расчетная схема – система общего вида, 4 стержневых элемента типа 10. Обеспечение граничных условий достигается: за счет наложения жестких связей по направлениям степеней свободы X, Z, UY и введением связей конечной жесткости по направлениям степеней свободы Y, UX, UZ (тип элемента 51) – для конца верхнего стержня пространственной системы (точка 5); за счет наложения жестких связей по направлениям степеней свободы Y, Z, UX и введением связей конечной жесткости по направлениям степеней свободы X, UY, UZ (тип элемента 51) – для конца нижнего стержня пространственной системы (точка 1). Количество узлов в расчетной схеме – 5.
Результаты решения в SCAD
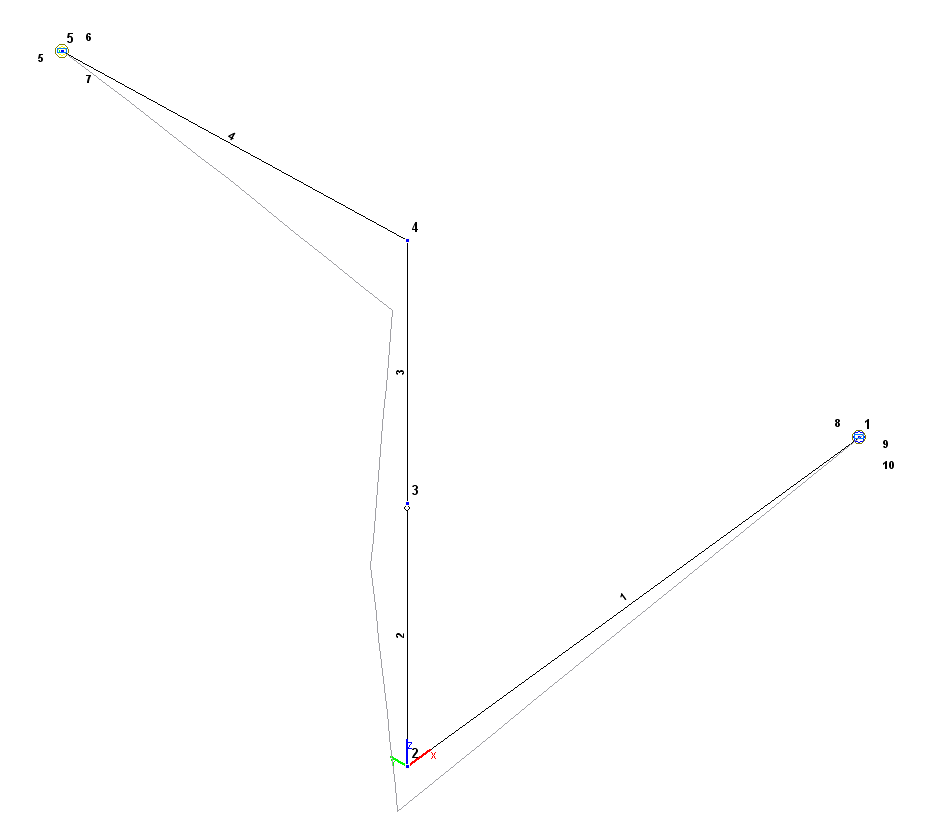
Расчетная и деформированная схемы
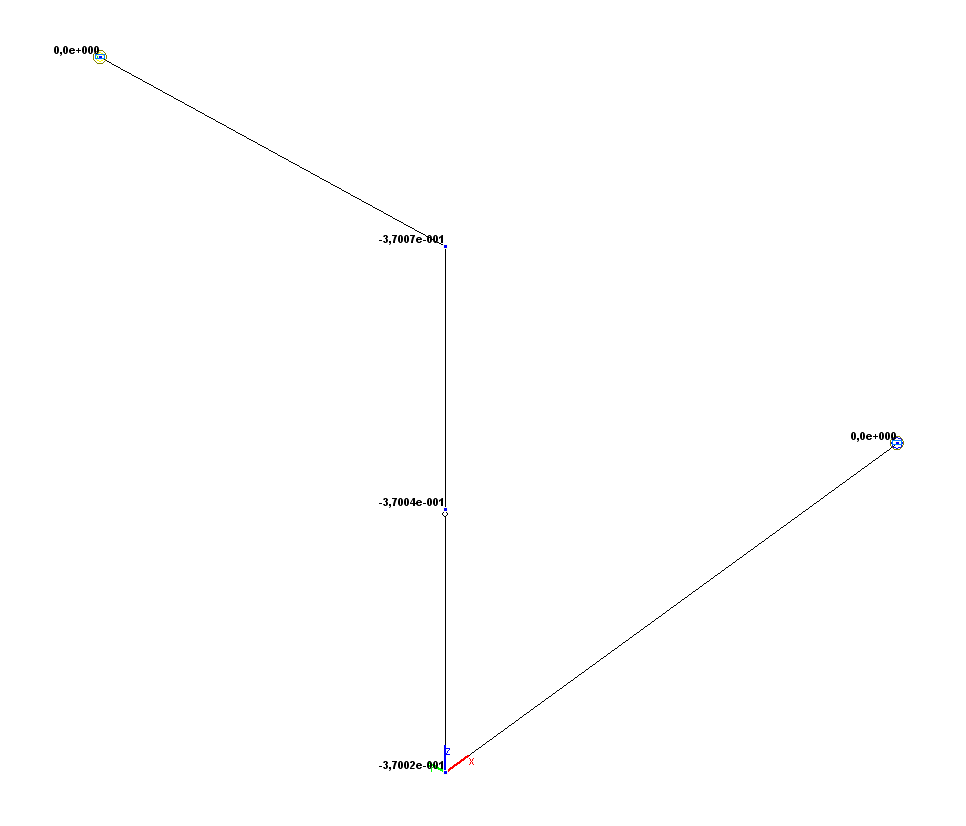
Значения вертикальных перемещений Z (м)
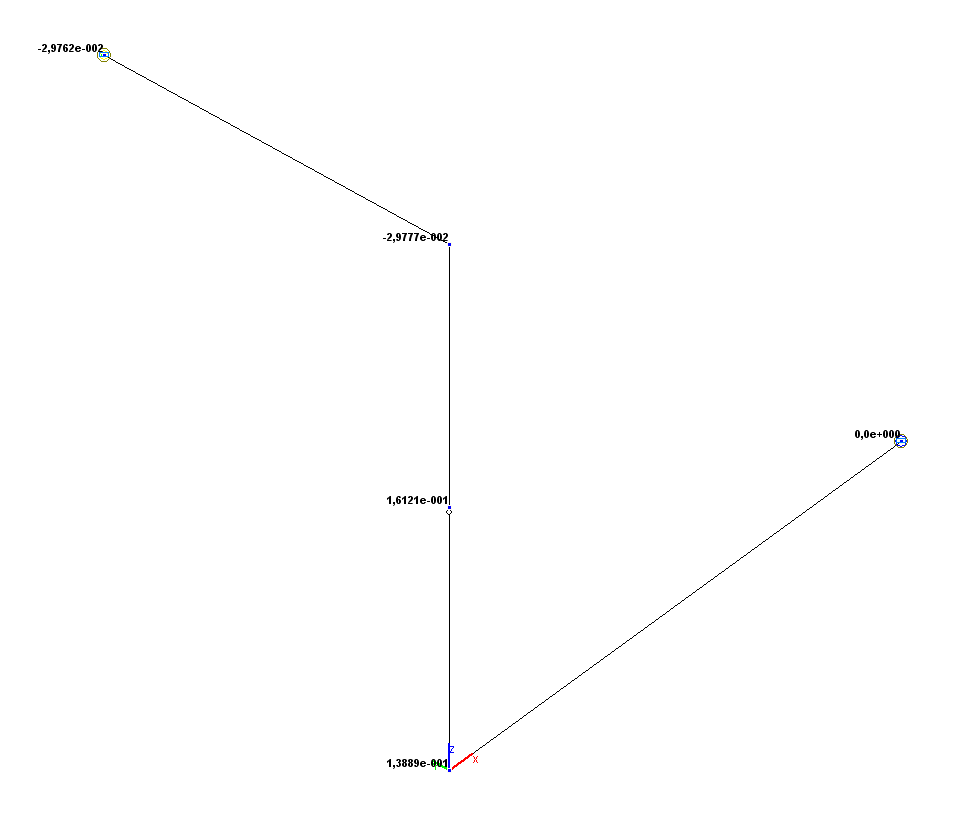
Значения горизонтальных перемещений Y (м)
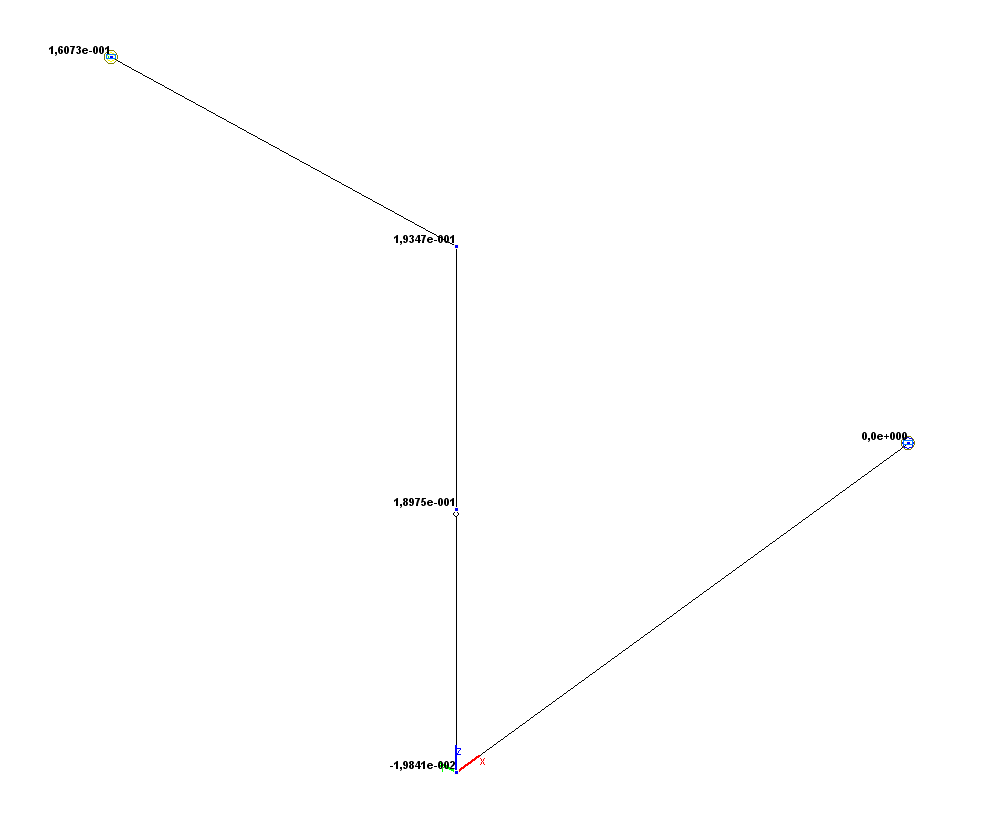
Значения углов поворота UX (рад)
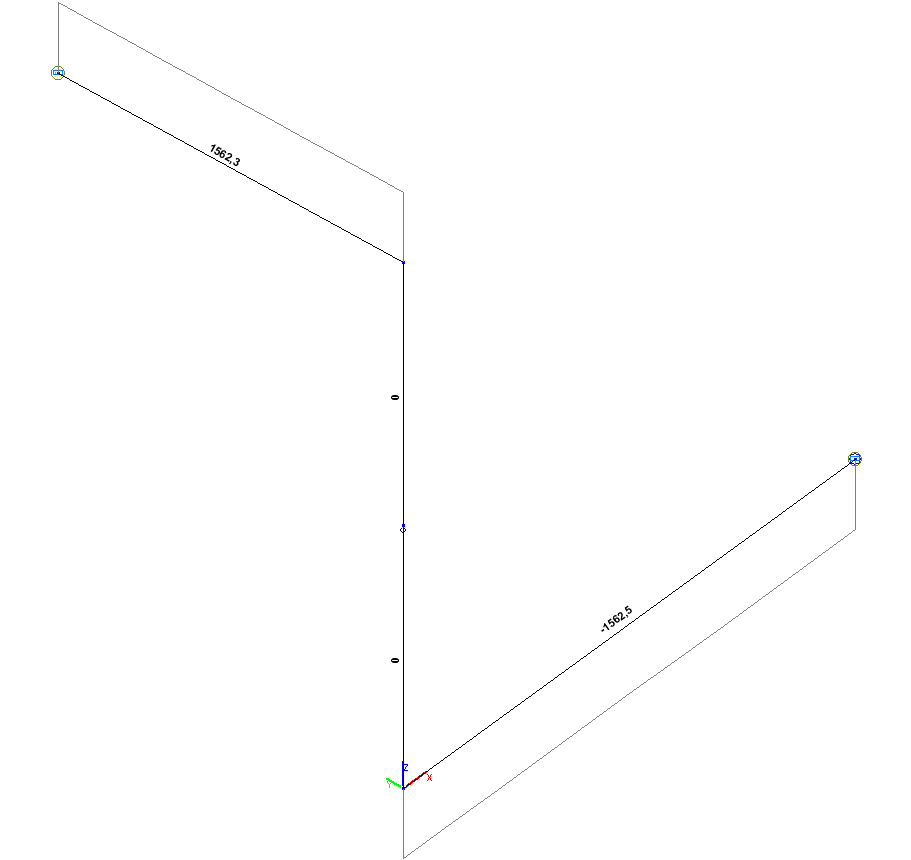
Эпюра крутящих моментов Мx (кН*м)
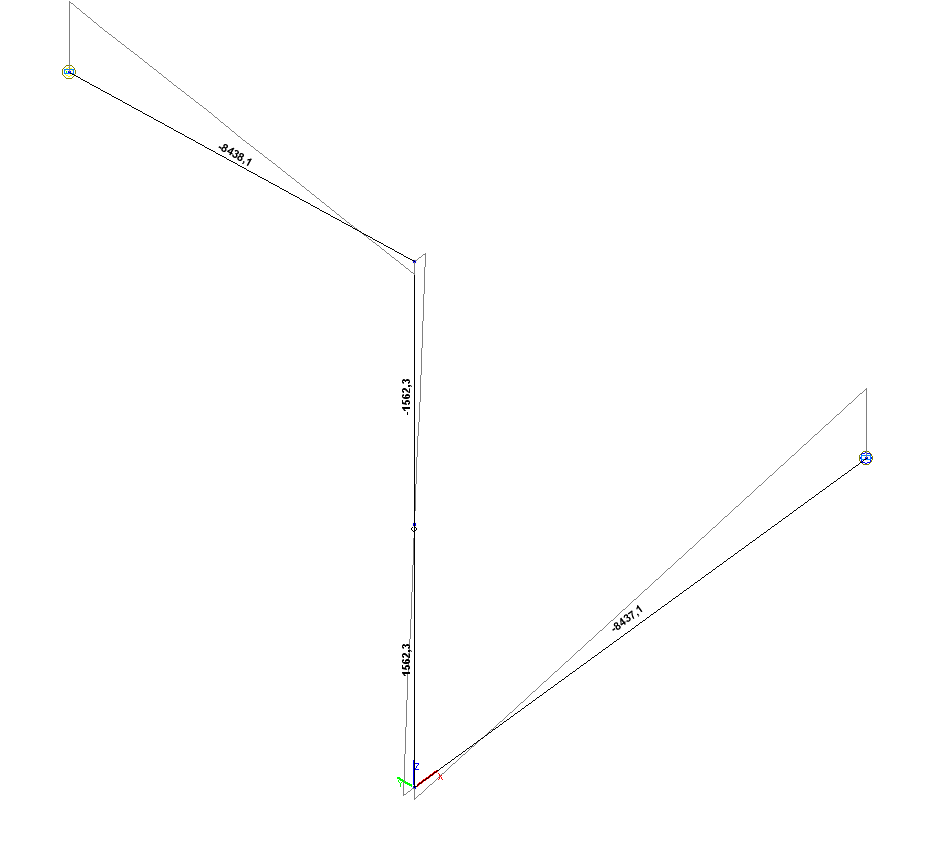
Эпюра изгибающих моментов Мy (кН*м)

Эпюра изгибающих моментов Мz (кН*м)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Вертикальное перемещение Z (точка 3), м |
-3.7004·10-1 |
-3.7004·10-1 |
0.00 |
|
Горизонтальное перемещение Y (точка 5), м |
-2.9762·10-2 |
-2.9762·10-2 |
0.00 |
|
Угол поворота UX (точка 5), рад |
1.6071·10-1 |
1.6073·10-1 |
0.01 |
|
Крутящий момент Mx (точка 5), Н·м |
1562.5 |
1562.3 |
0.01 |
|
Изгибающий момент My (точка 5), Н·м |
-8437.5 |
-8438.1 |
0.01 |
|
Изгибающий момент Mz (точка 5), Н·м |
-3125.0 |
3124.6 |
0.01 |
|
Крутящий момент Mx (точка 1), Н·м |
-1562.5 |
-1562.5 |
0.00 |
|
Изгибающий момент My (точка 1), Н·м |
-8437.5 |
-8437.1 |
0.00 |
|
Изгибающий момент Mz (точка 1), Н·м |
3125.0 |
3125.0 |
0.00 |
