Кольцо, нагруженное в его плоскости распределенной нагрузкой
Цель: Расчет изгиба в плоскости кольца под распределенной силой, без учета деформаций поперечного сдвига.
Файл с исходными данными: 4_7.spr
Формулировка задачи: Кольцо нагружается в его плоскости распределенной нагрузкой q. Определить: нормальную силу в сечении кольца N и изменения диаметра кольца δ.
Ссылки: Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988.
Исходные данные:
| E = 2.0·1011 Па | - модуль упругости, |
| μ = 0.3 | - коэффициент Пуассона, |
| R= 1 м | - радиус кольца; |
| F = 0,001 м2 | - площадь поперечного сечения; |
| q = 100 кН/м | - значение распределенной нагрузки. |
Конечноэлементная модель: Расчетная схема – общего вида, 72 стержневых конечных элемента, 72 узла.
Результаты решения в SCAD
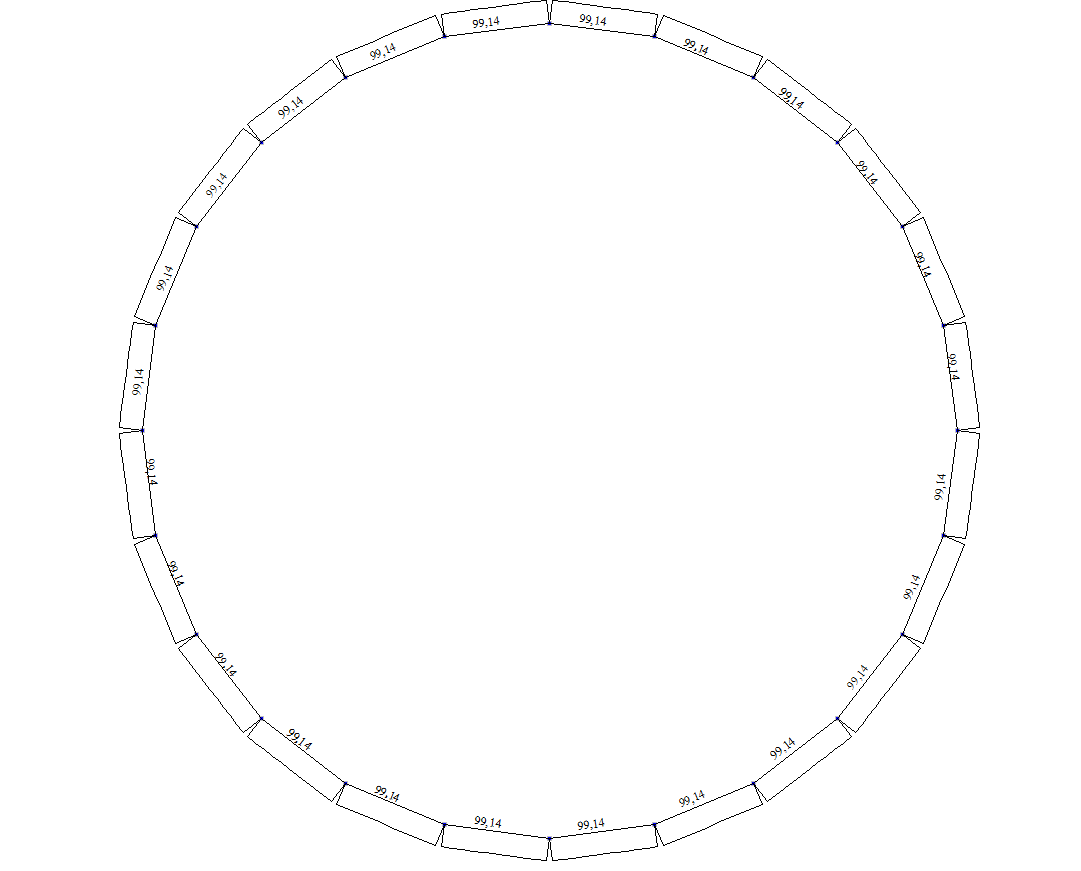
Эпюра нормальной силы N (кН)
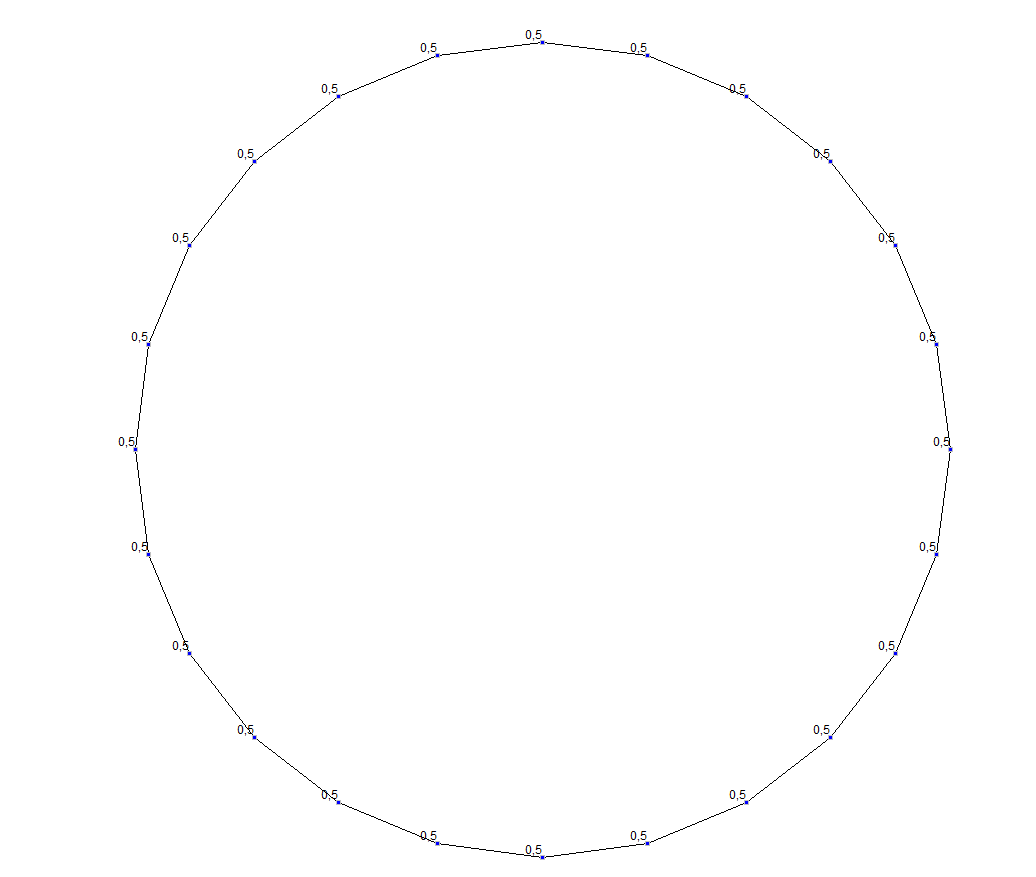
Значение перемещений δmax (мм)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Изменение диаметра кольца δ, мм |
0.50 |
0.50 |
0.00 |
|
Нормальная сила в сечении кольца N, кН |
100.00 |
99.14 |
0.86 |
Замечания: При аналитическом решении изменение диаметра кольца в направлениях осей x и y определяется по формулам ( «Справочник по сопротивлению материалов» стр. 384) :
\[ \delta_{x} =\delta_{y} =\frac{q\cdot R^{2}}{E\cdot F}. \]
Нормальная сила в сечении кольца:
\[ N=q\cdot R. \]
