Полуциркульная арка постоянного поперечного сечения с шарнирным опиранием под действием сосредоточенной силы в ее плоскости

Цель: Определение деформированного состояния полуциркульной арки постоянного поперечного сечения с шарнирным опиранием от воздействия сосредоточенной силы в ее плоскости.

Файл с исходными данными: SSLL08_v11.3.spr

Формулировка задачи: Полуциркульная арка постоянного поперечного сечения, имеющая в уровне пят шарнирно-неподвижную и шарнирно-подвижную опоры, нагружена в своей плоскости в уровне замка сосредоточенной силой F, направленной по нормали к продольной оси в сторону пят. Определить прогиб продольной оси арки Z, смещение  шарнирно-подвижной опоры X и углы поворота опорных шарниров UY.

Ссылки: P. Dellus, Resistance de materiaux, Paris, Technique et Vulgarisation, 1958. 

Исходные данные:

E = 2.0·1011  Па	- модуль упругости полуциркульной арки;
r = 1.0 м	- радиус дуги продольной оси полуциркульной арки;
de = 0.020 м	- наружный диаметр кольцевого поперечного сечения арки;
di = 0.016 м	- внутренний диаметр кольцевого поперечного сечения арки;
F = 100 Н	- значение сосредоточенной силы.

Конечноэлементная модель: Расчетная  схема – плоская рама, 48 стержневых элемента типа 10. Обеспечение граничных условий достигается: за счет наложения связей по направлениям степеней свободы X, Z – для шарнирно-неподвижной опоры и Z – для шарнирно-подвижной опоры. Количество узлов в расчетной схеме – 49.

Результаты решения в SCAD

 
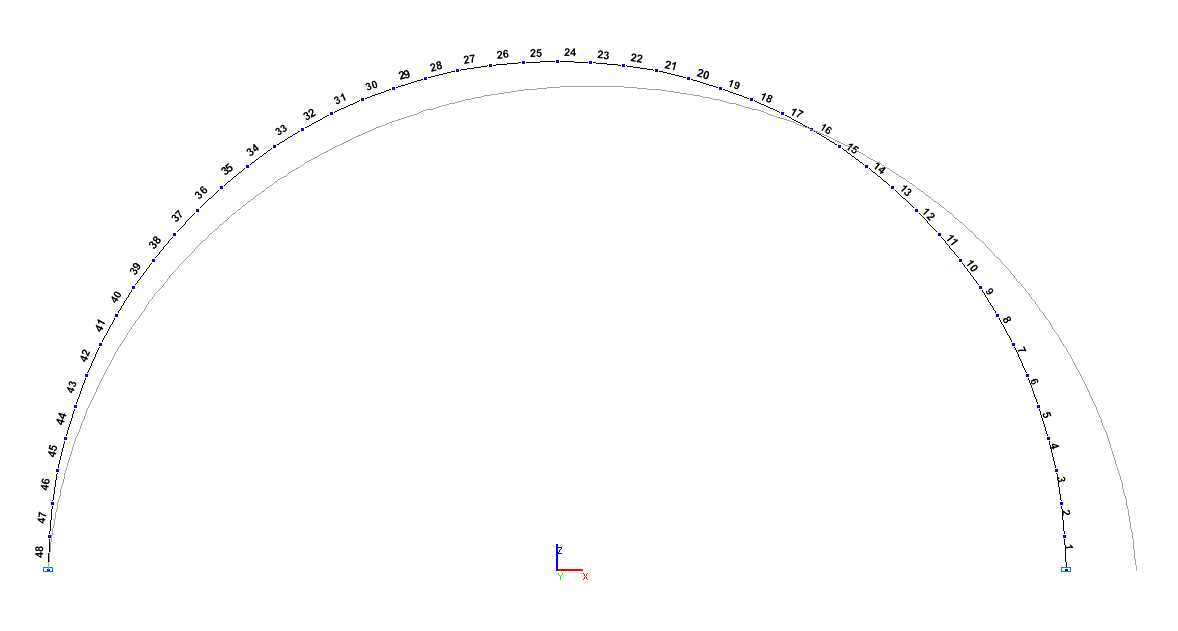
Расчетная и деформированная схемы

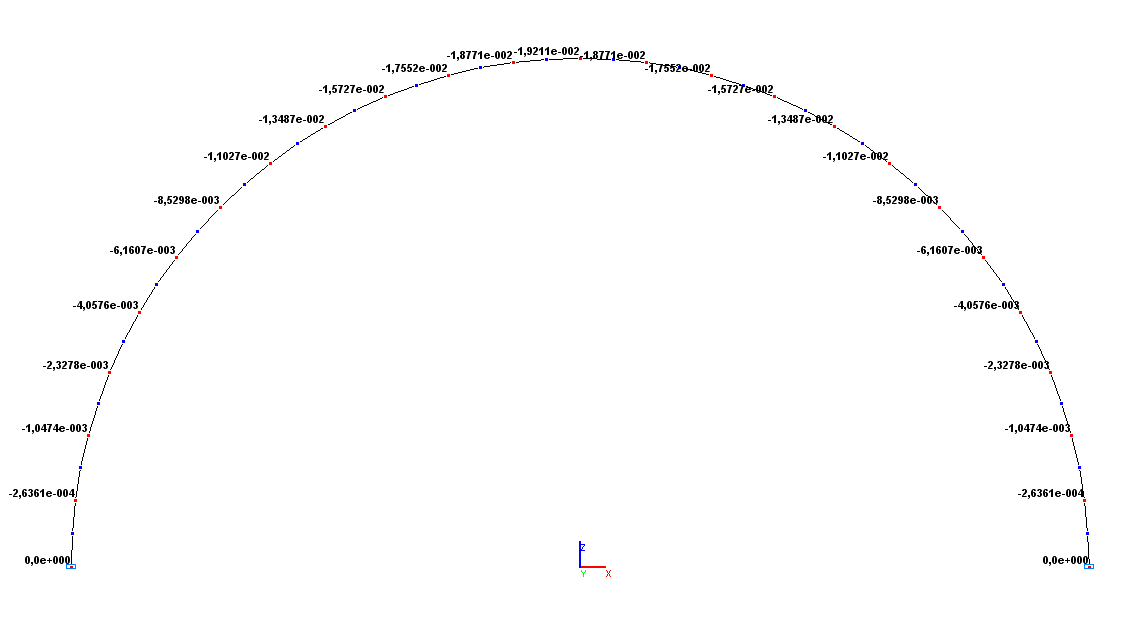
Значения вертикальных перемещений Z (м)

Значения горизонтальных перемещений X (м)

Значения углов поворота UY (рад)

 

Сравнение решений:

 

Параметр	Теория	SCAD	Отклонения, %
Прогиб продольной оси арки Z, м	-1.9206·10-2	-1.9211·10-2	0.03
Смещение шарнирно-подвижной опоры X, м	5.3912·10-2	5.3902·10-2	0.02
Угол поворота шарнирно-подвижной опоры UY, рад	-3.0774·10-2	-3.0788·10-2	0.05
Угол поворота шарнирно-неподвижной опоры UY, рад	3.0774·10-2	3.0788·10-2	0.05

Замечания: При аналитическом решении прогиб продольной оси арки Z, смещение  шарнирно-подвижной опоры X и углы поворота опорных шарниров UY определяются по следующим формулам:

\[Z=\frac{\pi }{8}\cdot \frac{F\cdot r}{E\cdot A}+\left( {\frac{3\cdot \pi }{8}-1} \right)\cdot \frac{F\cdot r^{3}}{E\cdot I}; \quad X=\frac{1}{2}\cdot \frac{F\cdot r}{E\cdot A}-\frac{1}{2}\cdot \frac{F\cdot r^{3}}{E\cdot I}; \quad UY=\pm \left( {\frac{\pi }{4}-\frac{1}{2}} \right)\frac{F\cdot r^{2}}{E\cdot I}, где: \] \[ I=\frac{\pi \cdot d_{e}^{2}}{4}\cdot \left( {1-\left( {\frac{d_{i} }{d_{e} }} \right)^{2}} \right); \quad I=\frac{\pi \cdot d_{e}^{4}}{64}\cdot \left( {1-\left( {\frac{d_{i} }{d_{e} }} \right)^{4}} \right). \]