Консольный кривой брус, нагруженный поперечной сосредоточенной силой на свободном конце

Сходимость решений для консольного кривого бруса:
1 – МКЭ-линейный; 2 – МКЭ-квадратичный; 3 – МСКЭ-линейный; 4 – МКЭ-сплайн;
5 – МСКЭ – сплайн; 6 – МСКЭ-квадратичный.

Цель: Проверка точности определения величины перемещения для свободного конца бруса по направлению действия сосредоточенной силы для моделей различных размерностей.

Файлы с исходными данными:

4.38_c.spr	Стержневая расчетная модель
4.38_p.spr	Оболочечная расчетная модель
4.38_о.spr	Объемная расчетная модель

Формулировка задачи: Консольный кривой брус с продольной осью кругового очертания, имеющей длину разрезного кольца, и с постоянным вдоль оси прямоугольным поперечным сечением нагружается на свободном конце поперечной сосредоточенной силой P. Определить перемещение свободного конца бруса w по направлению действия сосредоточенной силы.

Ссылки: А.С. Сахаров, И. Альтенбах. Метод конечных элементов в механике твердых тел. — Киев: Вища школа. 1982, Лейпциг: ФЕБ Фахбухферлаг. 1982;
Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов. — Киев: Наукова думка, 1975.

Исходные данные:

E = 100.0 кПа	- модуль упругости;
ν = 0.0	- коэффициент Пуассона;
R = 0.20 м	- радиус дуги продольной оси консольного кривого бруса;
α = 360º	- центральный угол длины дуги продольной оси консольного кривого бруса;
b = h = 0.01 м	- размеры поперечного сечения консольного кривого бруса;
P = 10-8 кН	- значение поперечной сосредоточенной силы на свободном конце бруса.

 

Конечноэлементная модель: Расчетная  схема – система общего вида. Рассматриваются три расчетные модели:

Стержневая модель (С), 120 элементов типа 5, сетка конечных элементов разбита по длине продольной оси с шагом 3.0º, 121 узел;

Оболочечная модель  (П), 480 восьмиузловых элементов типа 50, сетка конечных элементов разбита по длине продольной оси с шагом 3.0º, по высоте бруса с шагом 0.0025 м, 1689 узлов;

Объемная модель (О), 1920 двадцатиузловых элементов типа 37, сетка конечных элементов разбита по длине продольной оси с шагом 3.0º, по высоте  и ширине бруса с шагом 0.0025 м, 10865 узлов.

Результаты решения в SCAD

Расчетная схема. Стержневая модель

Расчетная схема. Оболочечная модель

Расчетная схема. Объемная модель

 
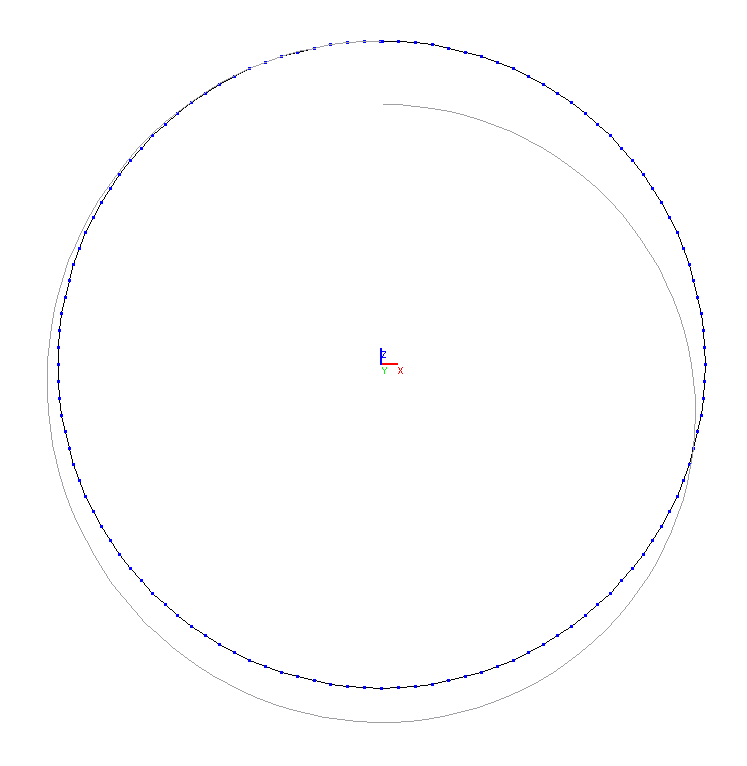
Деформированная схема и значения перемещения свободного конца бруса w в стержневой модели (мм)

 

Деформированная схема и значения перемещения свободного конца бруса w в оболочечной модели (мм)

 

Деформированная схема и значения перемещения свободного конца бруса w в объемной модели (мм)

 

Сравнение решений:

 

Модель	Перемещения w, мм	Отклонения, %
Стержневая (С)	3.015	0.03
Оболочечная (П)	3.017	0.03
Объемная (О)	3.017	0.03
Теория	3.016	-

Замечания: При аналитическом решении перемещение свободного конца бруса w по направлению действия поперечной сосредоточенной силы определяется по формуле (Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов. — Киев: Наукова думка, 1975, стр. 392):

\[ w=\frac{12\cdot P\cdot R^{3}}{E\cdot b\cdot h^{3}}\cdot \left( {\frac{\alpha }{2}-\frac{\sin \left( {2\cdot \alpha } \right)}{4}} \right). \]