Консольный круговой стержень постоянного поперечного сечения под действием в его плоскости сосредоточенных сил и момента на свободном конце
Цель: Определение деформированного состояния консольного кругового стержня постоянного поперечного сечения от действия в его плоскости сосредоточенных сил и момента на свободном конце.
Файл с исходными данными:
| SSLL06_вариант_1_v11.3.spr | Расчетная схема – плоская рама. Консольный круговой стержень расположен в плоскости XOZ общей системы координат |
Формулировка задачи: Консольный круговой стержень постоянного поперечного сечения нагружается на свободном конце сосредоточенными горизонтальной (нормальной) F1 и вертикальной (тангенциальной) F2 силами и моментом M, действующими в его плоскости. Определить горизонтальное X и вертикальное Z перемещения, а также угол поворота UY свободного конца стержня (точка B).
Ссылки: J.S. Przemieniecki, Theory of matrix structural analysis, New York, McGraw-Hill, 1968.
Исходные данные:
| E = 2.0·1011 Па | - модуль упругости консольного кругового стержня; |
| r = 3.0 м | - радиус дуги продольной оси консольного кругового стержня; |
| α = 90º | - центральный угол длины дуги продольной оси консольного кругового стержня; |
| de = 0.020 м | - наружный диаметр кольцевого поперечного сечения стержня; |
| di = 0.016 м | - внутренний диаметр кольцевого поперечного сечения стержня; |
| F1 = 10 Н | - значение горизонтальной сосредоточенной силы; |
| F2 = 5 Н | - значение вертикальной сосредоточенной силы; |
| M = 8 Н∙м | - значение сосредоточенного момента. |
Конечноэлементная модель: Расчетная схема – плоская рама, 24 стержневых элемента типа 10. Обеспечение граничных условий достигается: за счет наложения связей по направлениям степеней свободы X, Z, UY (точка A). Количество узлов в расчетной схеме – 25.
Результаты решения в SCAD

Расчетная и деформированная схемы

Значения горизонтальных перемещений X (м)
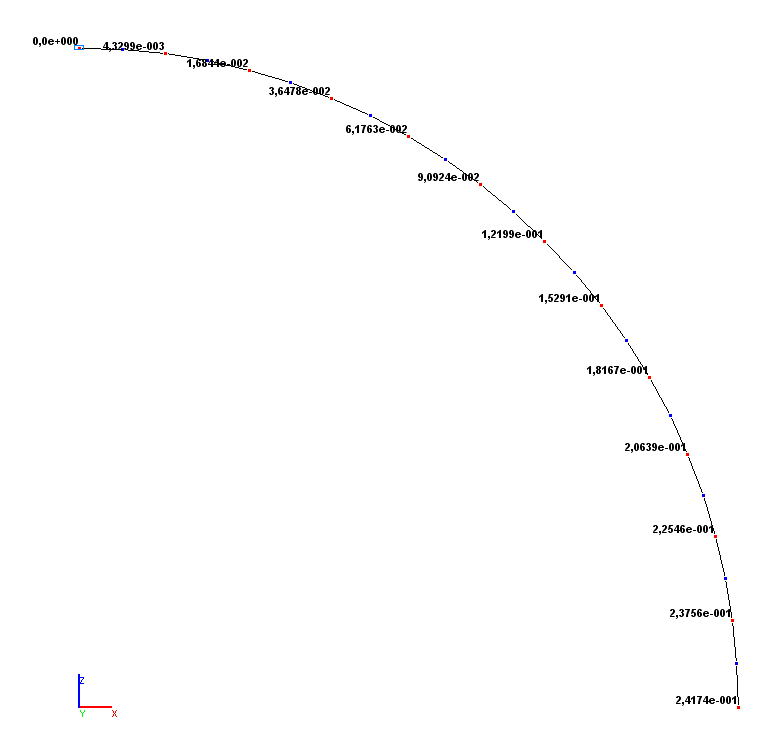
Значения вертикальных перемещений Z (м)
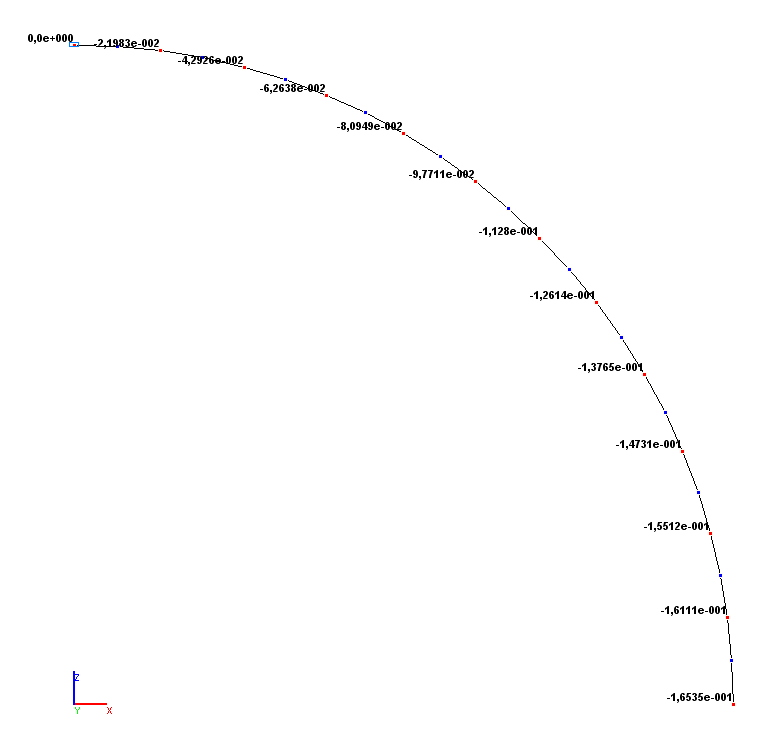
Значения углов поворота UY (рад)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Горизонтальное перемещение X (точка B), м |
3.7908·10-1 |
3.7882·10-1 |
0.07 |
|
Вертикальное перемещение Z (точка B), м |
2.4173·10-1 |
2.4174·10-1 |
0.01 |
|
Угол поворота UY (точка B), рад |
-1.6539·10-1 |
-1.6535·10-1 |
0.02 |
Замечания: При аналитическом решении горизонтальное X и вертикальное Z перемещения, а также угол поворота UY свободного конца стержня определяются по следующим формулам:
\[ X=\frac{r^{2}}{E\cdot I}\cdot \left( {M+F1\cdot r\cdot \frac{\pi }{4}+F2\cdot r\cdot \frac{1}{2}} \right); \] \[ Z=\frac{r^{2}}{E\cdot I}\cdot \left( {M\cdot \left( {\frac{\pi }{2}-1} \right)+F1\cdot r\cdot \frac{1}{2}+F2\cdot r\cdot \left( {\frac{3\cdot \pi }{4}-2} \right)} \right); \] \[ UY=-\frac{r}{E\cdot I}\cdot \left( {M\cdot \frac{\pi }{2}+F1\cdot r+F2\cdot r\cdot \left( {\frac{\pi }{2}-1} \right)} \right), где: \] \[ I=\frac{\pi \cdot d_{e}^{4}}{64}\cdot \left( {1-\left( {\frac{d_{i} }{d_{e} }} \right)^{4}} \right). \]
