Двухпролетная одноэтажная рама под действием постоянной поперечной единичной силы, перемещающейся вдоль пролетов ригеля с малой скоростью. Построение линий влияния внутренних усилий в сечениях рамы
Цель: Определение значений изгибающего момента в сечении середины левого пролета ригеля двухпролетной одноэтажной рамы в зависимости от положения постоянной поперечной единичной силы, перемещающейся вдоль пролетов ригеля с малой скоростью.
Файл с исходными данными: Influence_Line.spr
Формулировка задачи: Вдоль ригеля двухпролетной одноэтажной рамы перемещается с малой скоростью постоянная поперечная единичная сила P. Ригель жестко сопряжен со средней и крайней правой стойками, которые имеют шарнирное опирание, и свободно оперт краем левого пролета. Определить значения изгибающего момента в сечении середины левого пролета ригеля рамы M1-1 в зависимости от положения поперечной силы и построить линию влияния.
Ссылки: А. Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников, Строительная механика. Стержневые системы, Москва, Стройиздат, 1981, стр. 352-356.
Исходные данные:
| l = 6.0 м | - длина ригелей рамы; |
| h = 6.0 м | - высота стоек рамы; |
| EA = 1.0·106 кН | - продольная жесткость конструктивных элементов рамы; |
| EI = 83.3333 кН·м2 | - изгибная жесткость конструктивных элементов рамы; |
| P = 1.0 кН | - значение поперечной единичной силы. |
Конечноэлементная модель: Расчетная схема – плоская рама, 24 элемента типа 2. Сетка конечных элементов разбита по длинам продольных осей конструктивных элементов (вдоль осей X1 местных систем координат) с шагом 1.0 м. Обеспечение граничных условий достигается за счет наложения связей на опорные узлы стоек по направлениям степеней свободы X, Z и на опорный узел левого пролета ригеля по направлению степени свободы Z.
Задача решается кинематическим методом:
- производится разделение элементов середины левого пролета ригеля с образованием пары совпадающих узлов, каждый из которых принадлежит одному из этих смежных элементов;
- для пары совпадающих узлов объединяются перемещения по всем степеням свободы, кроме UY;
- к узлам пары прикладываются единичные сосредоточенные противоположные по знаку изгибающие моменты My = 1.0 кН•м.
Результат линии влияния изгибающего момента в сечении середины левого пролета рамы [узлы 26, 8] следует смотреть в виде деформаций по формуле: -Z/[UY26-UY8]/1000. Делить выражение на 1000 необходимо, если размерность Z задана в мм.
Количество узлов в расчетной схеме – 26.
Результаты решения в SCAD
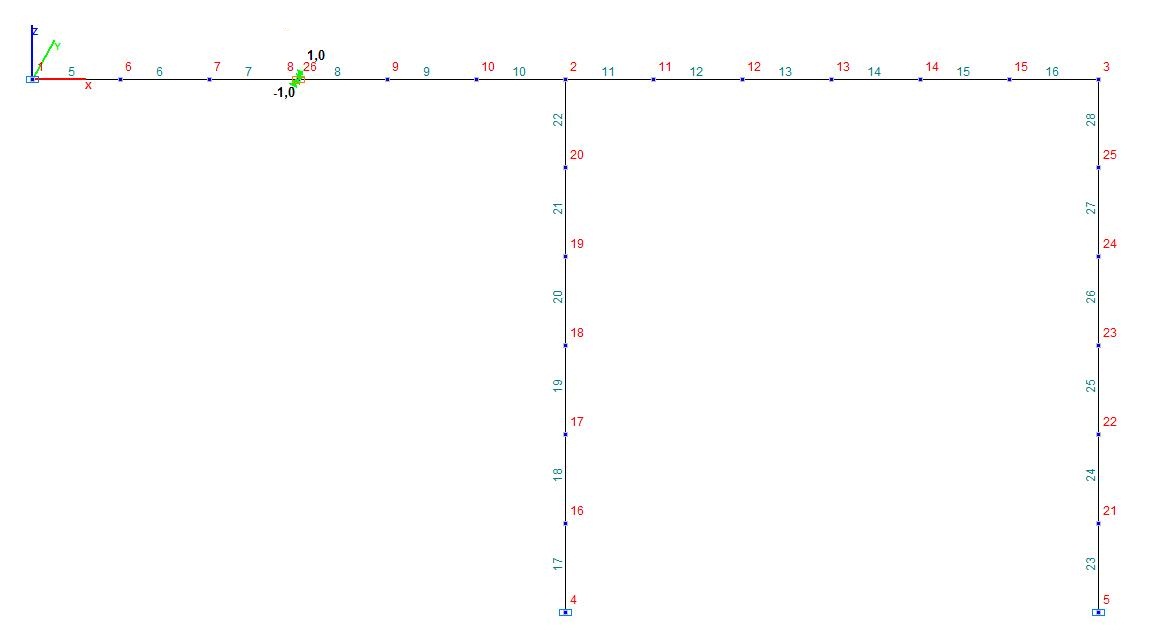
Расчетная схема

Значения углов поворота UY (рад)

Значения изгибающего момента в сечении середины левого пролета ригеля рамы M1-1 (кН∙м) в зависимости от положения поперечной силы
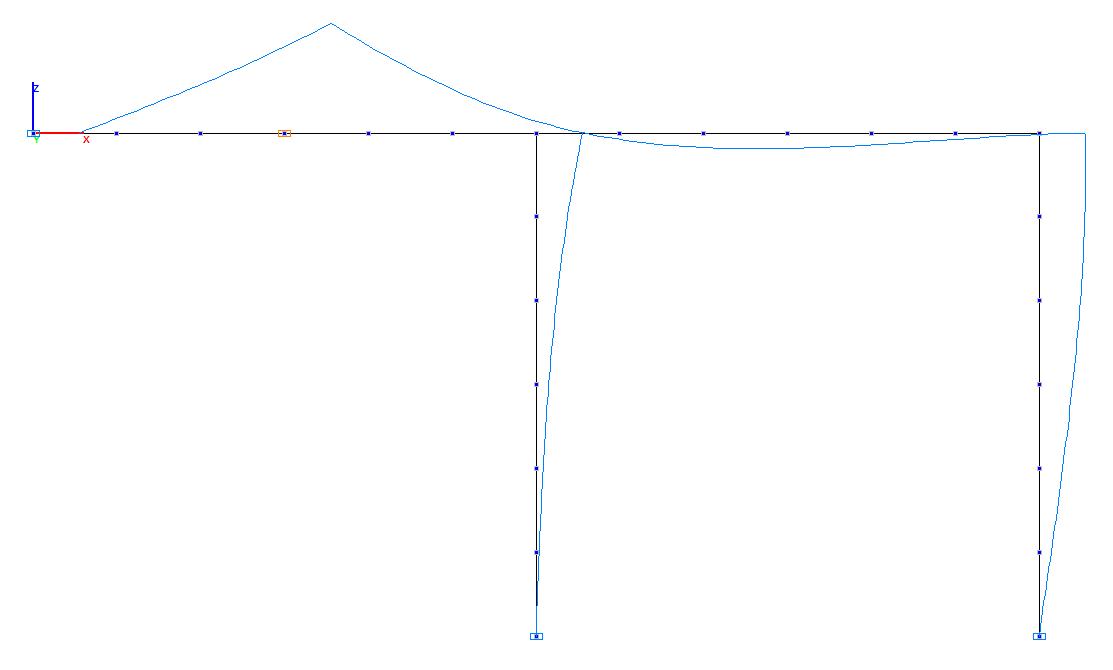
Линия влияния изгибающего момента в сечении середины левого пролета ригеля рамы M1-1
Сравнение решений:
Значения изгибающего момента в сечении середины левого пролета ригеля рамы M1-1 (кН•м) в зависимости от положения поперечной силы
|
Положение поперечной силы от края левого пролета, м |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
0.00 |
0.000 |
0.000 |
0.00 |
|
1.00 |
0.343 |
0.343 |
0.00 |
|
2.00 |
0.714 |
0.713 |
0.14 |
|
3.00 |
1.137 |
1.137 |
0.00 |
|
4.00 |
0.641 |
0.642 |
0.16 |
|
5.00 |
0.254 |
0.254 |
0.00 |
|
6.00 |
0.000 |
0.000 |
0.00 |
|
7.00 |
-0.125 |
-0.125 |
0.00 |
|
8.00 |
-0.165 |
-0.165 |
0.00 |
|
9.00 |
-0.144 |
-0.145 |
0.69 |
|
10.00 |
-0.093 |
-0.093 |
0.00 |
|
11.00 |
-0.036 |
-0.036 |
0.00 |
|
12.00 |
0.000 |
0.000 |
0.00 |
