Изгиб прямоугольной балки-стенки, жестко подвешенной по боковым сторонам, под действием равномерно распределенной нагрузки, расположенной на верхней стороне
Цель: Определение деформированного состояния прямоугольной балки-стенки, жестко подвешенной по боковым сторонам, от воздействия равномерно распределенной нагрузки, расположенной на верхней стороне.
Файл с исходными данными: KSLS01_v11.3.spr
Формулировка задачи: К верхней стороне прямоугольной балки-стенки, жестко подвешенной по боковым сторонам, приложена равномерно распределенная нагрузка p, действующая в плоскости балки-стенки по оси y. Определить компоненты тензора перемещений в декартовых координатах u(x,z) и v(x,z) для срединной поверхности балки-стенки в ее плоскости.
Ссылки: А.С. Калманок, Расчет балок-стенок, Москва, Госстройиздат, 1956.
Исходные данные:
| E = 2.65·106 Па | - модуль упругости; |
| ν = 0.15 | - коэффициент Пуассона; |
| h = 0.1 м | - толщина балки-стенки; |
| a = 1.6 м | - длина пролета балки-стенки; |
| b = 1.6 м | - высота балки-стенки; |
| p = 500.0 Н/м | - равномерно распределенная нагрузка. |
Конечноэлементная модель: Расчетная схема - плоская шарнирно-стержневая система, 200 элементов балки-стенки типа 21. Сетка конечных элементов разбита с шагом 0.08 м в направлениях осей x и z общей системы координат. Обеспечение граничных условий достигается за счет наложения связей по направлению степени свободы Z для боковой стороны и по направлению степени свободы X на оси симметрии. Количество узлов в расчетной схеме – 231.
Результаты решения в SCAD


Расчетная схема

Деформированная схема
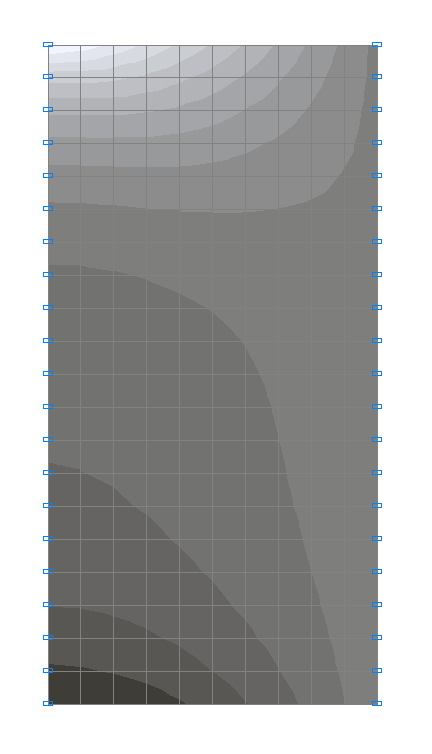

Значения перемещений вдоль пролета балки-стенки u (м)
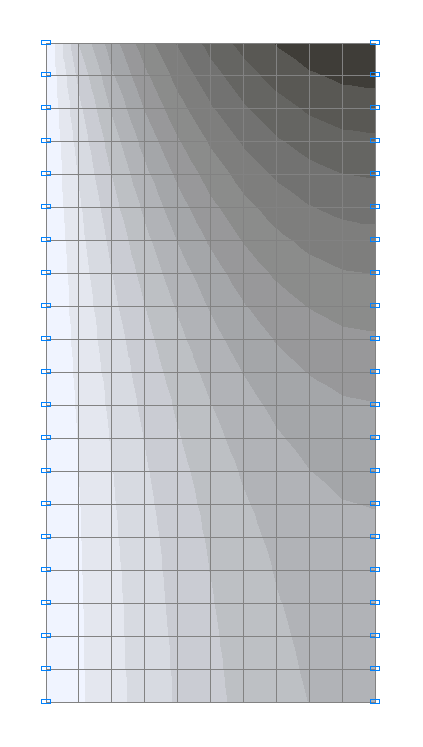

Значения перемещений по высоте балки-стенки v (м)
Сравнение решений:
|
Координаты |
Перемещения u, м |
Перемещения v, м |
|||||
|---|---|---|---|---|---|---|---|
|
x |
z |
Теория |
SCAD |
Отклонения, % |
Теория |
SCAD |
Отклонения, % |
|
0.0 |
0.0 |
-0.719•10-3 |
-0.713•10-3 |
0.83 |
0.000•10-3 |
0.000•10-3 |
- |
|
0.0 |
0.8 |
-0.220•10-3 |
-0.221•10-3 |
0.45 |
0.000•10-3 |
0.000•10-3 |
- |
|
0.0 |
1.6 |
1.468•10-3 |
1.401•10-3 |
4.56 |
0.000•10-3 |
0.000•10-3 |
- |
|
0.4 |
0.0 |
-0.508•10-3 |
-0.504•10-3 |
0.79 |
-0.672•10-3 |
-0.667•10-3 |
0.74 |
|
0.4 |
0.8 |
-0.148•10-3 |
-0.148•10-3 |
0.00 |
-0.950•10-3 |
-0.945•10-3 |
0.53 |
|
0.4 |
1.6 |
0.780•10-3 |
0.778•10-3 |
0.26 |
-2.032•10-3 |
-2.027•10-3 |
0.25 |
|
0.8 |
0.0 |
0.000•10-3 |
0.000•10-3 |
- |
-0.950•10-3 |
-0.943•10-3 |
0.74 |
|
0.8 |
0.8 |
0.000•10-3 |
0.000•10-3 |
- |
-1.326•10-3 |
-1.320•10-3 |
0.45 |
|
0.8 |
1.6 |
0.000•10-3 |
0.000•10-3 |
- |
-2.510•10-3 |
-2.504•10-3 |
0.24 |
Замечания: При аналитическом решении компоненты тензора перемещений в декартовых координатах u(x,z) и v(x,z) для срединной поверхности балки-стенки в ее плоскости могут быть вычислены по следующим формулам:
\[
u\left( {x,z} \right)=-\frac{p\cdot b}{E\cdot h}\cdot
\sum\limits_{m=1}^{m=\infty } {\frac{a}{m\cdot \pi \cdot b}\cdot \left\{
{\left[ {2\cdot m\cdot \pi \cdot \frac{b}{a}\cdot sh\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right]\cdot \left[ {\left( {-2+\left( {1+\nu }
\right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right)\cdot sh\left( {m\cdot \pi \cdot \frac{b-z}{a}}
\right)-} \right.} \right.}
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b-z}{a}\cdot
ch\left( {m\cdot \pi \cdot \frac{b-z}{a}} \right)} \right]-\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)+\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {-2+\left(
{1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot
\pi \cdot \frac{b}{a}} \right)} \right)\cdot sh\left( {m\cdot \pi \cdot
\frac{z}{a}} \right)} \right.-
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{z}{a}\cdot
ch\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]-\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)-\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {2\cdot \nu
+\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left(
{m\cdot \pi \cdot \frac{b}{a}} \right)} \right)\cdot sh\left( {m\cdot \pi
\cdot \frac{z}{a}} \right)-} \right.
\]
\[
\left. {\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot
\frac{z}{a}\cdot ch\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]}
\right\} \cdot \frac{\left[ {1+\left( {-1} \right)^{m+1}} \right]\cdot
cos\left( {m\cdot \pi \cdot \frac{x}{a}} \right)}{m\cdot \pi \cdot sh\left(
{m\cdot \pi \cdot \frac{b}{a}} \right)\cdot \left[ {sh^{2}\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)-\left( {m\cdot \pi \cdot \frac{b}{a}}
\right)^{2}} \right]};
\]
\[
v\left( {x,z} \right)=\frac{p\cdot b}{E\cdot h}\cdot
\sum\limits_{m=1}^{m=\infty } {\frac{a}{m\cdot \pi \cdot b}\cdot \left\{
{\left[ {2\cdot m\cdot \pi \cdot \frac{b}{a}\cdot sh\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right]\cdot \left[ {\left( {1-\nu +\left( {1+\nu }
\right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right)\cdot ch\left( {m\cdot \pi \cdot \frac{b-z}{a}}
\right)-} \right.} \right.}
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b-z}{a}\cdot
sh\left( {m\cdot \pi \cdot \frac{b-z}{a}} \right)} \right]+\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)+\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {1-\nu +\left(
{1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot
\pi \cdot \frac{b}{a}} \right)} \right)\cdot ch\left( {m\cdot \pi \cdot
\frac{z}{a}} \right)} \right.-
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{z}{a}\cdot
sh\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]+\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)-\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {3+\nu +\left(
{1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot
\pi \cdot \frac{b}{a}} \right)} \right)\cdot ch\left( {m\cdot \pi \cdot
\frac{z}{a}} \right)-} \right.
\]
\[
\left. {\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot
\frac{z}{a}\cdot sh\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]}
\right\} \cdot \frac{\left[ {1+\left( {-1} \right)^{m+1}} \right]\cdot
sin\left( {m\cdot \pi \cdot \frac{x}{a}} \right)}{m\cdot \pi \cdot sh\left(
{m\cdot \pi \cdot \frac{b}{a}} \right)\cdot \left[ {sh^{2}\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)-\left( {m\cdot \pi \cdot \frac{b}{a}}
\right)^{2}} \right]}.
\]
