Изгиб симметричного клина сосредоточенным моментом, приложенным к его вершине (задача Инглиса)

Цель: Определение напряженного состояния симметричного клина единичной толщины в полярных координатах при изгибе сосредоточенным моментом, приложенным к его вершине.

Файл с исходными данными: 4_23.spr

Формулировка задачи: К вершине клина, толщина которого равна единице, приложен момент M, действующий в плоскости клина X₁OX₂. Определить компоненты тензора напряжений в полярных координатах σ_rr, σ_θθ, σ_rθ на радиальном расстоянии r = 5.0 м от вершины клина.

Ссылки: С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979.

Исходные данные:

E = 3.0·107 кПа	- модуль упругости;
μ = 0.2	- коэффициент Пуассона;
h = 1.0 м	- толщина клина;
2·α = 30º	- угол при вершине клина;
R = 15.0 м	- радиус закрепленного конца клина;
M = -25.0 кН	- сосредоточенный момент, изгибающий клин.

Конечноэлементная модель: Расчетная  схема – система общего вида, элементы клина – 280 восьмиузловых элементов типа 50. Сетка конечных элементов разбита с шагом 0.5 м в радиальном направлении и с шагом 3º в тангенциальном направлении. Направление выдачи внутренних усилий – радиально-тангенциальное. Ввиду того, что на цилиндрической поверхности малого радиуса a у вершины клина момент M не может быть представлен как равнодействующая напряжений, распределенных по закону аналитического решения, приведенного ниже, острие клина моделируется твердым телом с ведущим узлом при вершине клина и ведомыми узлами на радиальном расстоянии a = 1.0 м от вершины клина. Так как на закрепленном конце клин не испытывает усилий, распределенных по закону аналитического решения, для получения точного решения на радиальном расстоянии r = 5.0 м от воздействия момента M радиальное расстояние до закрепленного конца принято равным R = 15.0 м. Количество узлов в расчетной схеме – 918.

Результаты решения в SCAD

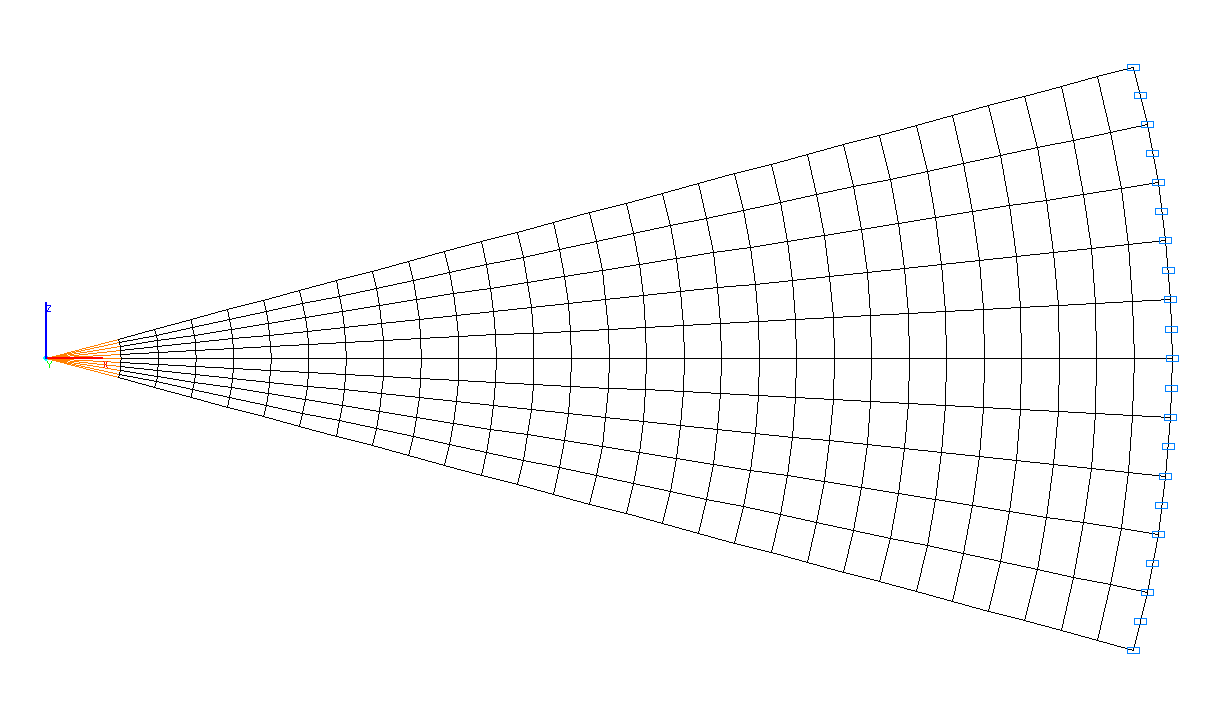
Расчетная схема

Значения напряжений σ_rr (кН/м²) при воздействии изгибающего момента M

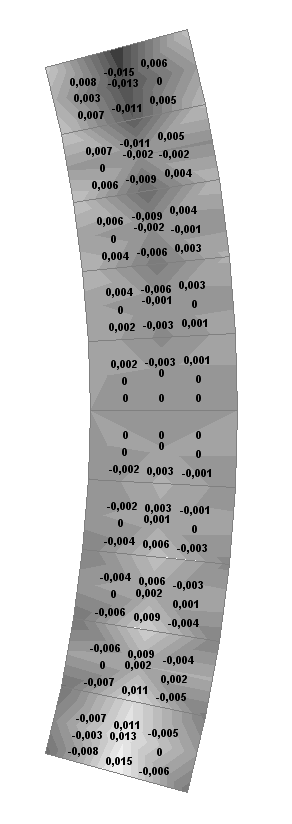
Значения напряжений σ_θθ (кН/м²) при воздействии изгибающего момента M

Значения напряжений σ_rθ (кН/м²) при воздействии изгибающего момента M

Сравнение решений:

Компоненты тензора напряжений на радиальном расстоянии r = 5.0 м от вершины клина при воздействии изгибающего момента M.

Угол θ	Напряжения σrr (кН/м2)
	Теория	SCAD	Отклонения, %
-15º	21.4822	21.4264	0.26
0º	0.0000	0.0000	-
+15º	-21.4822	-21.4264	0.26

 

Угол θ	Напряжения σθθ (кН/м2)
	Теория	SCAD	Отклонения, %
-15º	0.0000	-0.0059	-
0º	0.0000	0.0000	-
+15º	0.0000	0.0059	-

 

Угол θ	Напряжения σrθ (кН/м2)
	Теория	SCAD	Отклонения, %
-15º	0.0000	0.5071	-
0º	-2.8781	-2.9418	2.21
+15º	0.0000	0.5071	-

 

Замечания: При аналитическом решении напряжения σ_rr, σ_θθ, σ_rθ  в теле клина при воздействии изгибающего момента M определяются по следующим формулам (С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979, стр. 276):

\[ \sigma_{rr} =-\frac{2\cdot M\cdot \sin \left( {2\cdot \theta } \right)}{r^{2}\cdot \left( {2\cdot \alpha -tg\left( {2\cdot \alpha } \right)} \right)\cdot \cos \left( {2\cdot \alpha } \right)}; \quad \sigma_{\theta \theta } =0; \quad \sigma_{r\theta } =\frac{M\cdot \left( {\cos \left( {2\cdot \alpha } \right)-\cos \left( {2\cdot \theta } \right)} \right)}{r^{2}\cdot \left( {2\cdot \alpha -tg\left( {2\cdot \alpha } \right)} \right)\cdot \cos \left( {2\cdot \alpha } \right)}. \]