Плотина треугольной формы, воспринимающая воздействия собственного веса и гидростатического давления
Цель: Определение напряженного состояния плотины треугольной формы единичной толщины в декартовых координатах от воздействия собственного веса и гидростатического давления.
Файл с исходными данными: 4_25.spr
Формулировка задачи: К поверхности вертикальной грани плотины треугольной формы, толщина которой равна единице, приложена горизонтальная нагрузка, распределенная по линейному закону с весом единицы объема γ, действующая в плоскости плотин. Плотина также находится под действием собственного веса γ1. Определить компоненты тензора напряжений в декартовых координатах σx, σy, τxy в горизонтальном сечении плотины, расположенном на глубине y0 = 5.0 м от вершины плотины.
Ссылки: В.И. Самуль, Основы теории упругости и пластичности. — Москва: Высшая школа, 1982.
Исходные данные:
| E = 3.0·107 кПа | - модуль упругости материала плотины; |
| μ = 0.2 | - коэффициент Пуассона материала плотины; |
| h = 1.0 м | - толщина плотины; |
| β = 30º | - угол при вершине плотины; |
| H = 15.0 м | - высота плотины; |
| γ = 10.0 кН/м3 | - удельный вес жидкости; |
| γ1 = 20.0 кН/м3 | - удельный вес материала плотины. |
Конечноэлементная модель: Расчетная схема – типа плоская рама, элементы пластины – 452 восьмиузловых элемента типа 30 и 23 шестиузловых элемента типа 25. Сетка конечных элементов разбита с шагом 0.25 м в горизонтальном OX и вертикальном OY направлениях. Направление выдачи внутренних усилий – вдоль осей OX и OY глобальной системы координат. Так как на закрепленном конце плотина не испытывает усилий, распределенных по закону аналитического решения, для получения точного решения на глубине y0 = 5.0 м от вершины плотины при воздействии собственного веса и гидростатического давления высота плотины до закрепленного конца принята равной H = 15.0 м. Количество узлов в расчетной схеме – 1506.
Результаты решения в SCAD
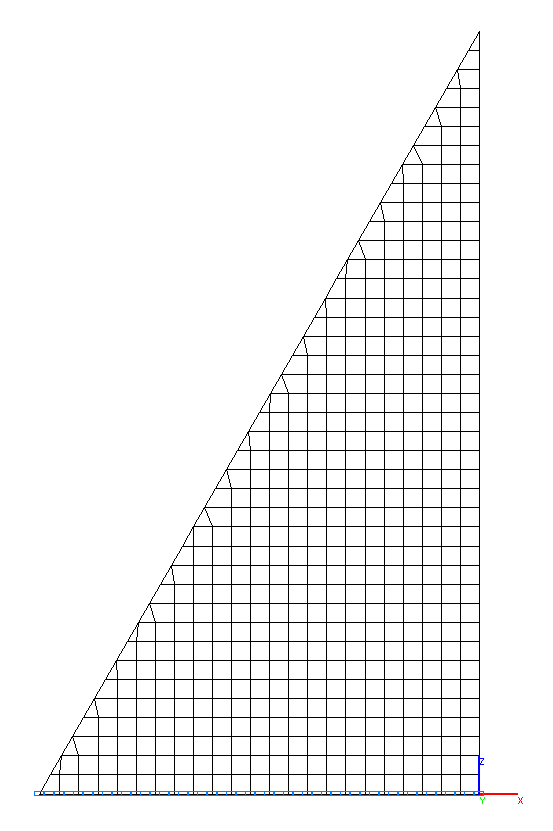
Расчетная схема
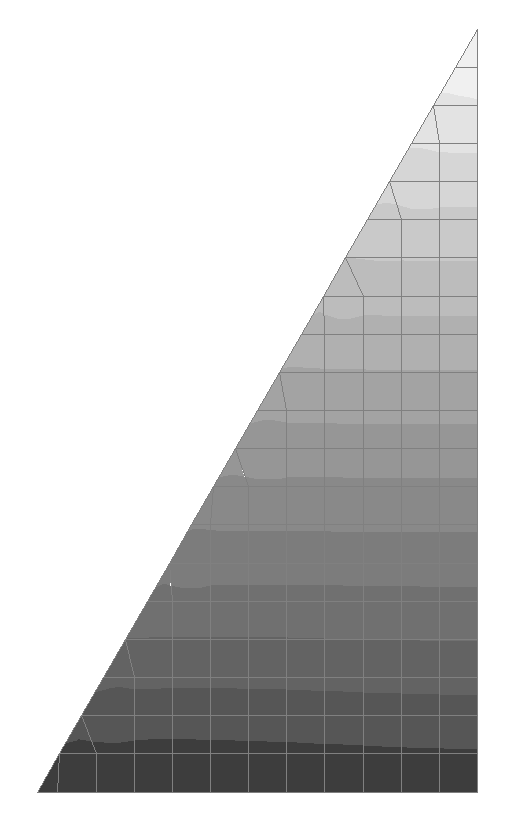
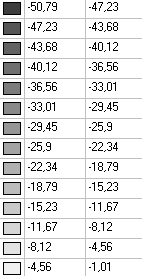
Значения напряжений σx (кН/м2)

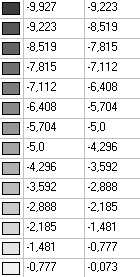
Значения напряжений σy (кН/м2)
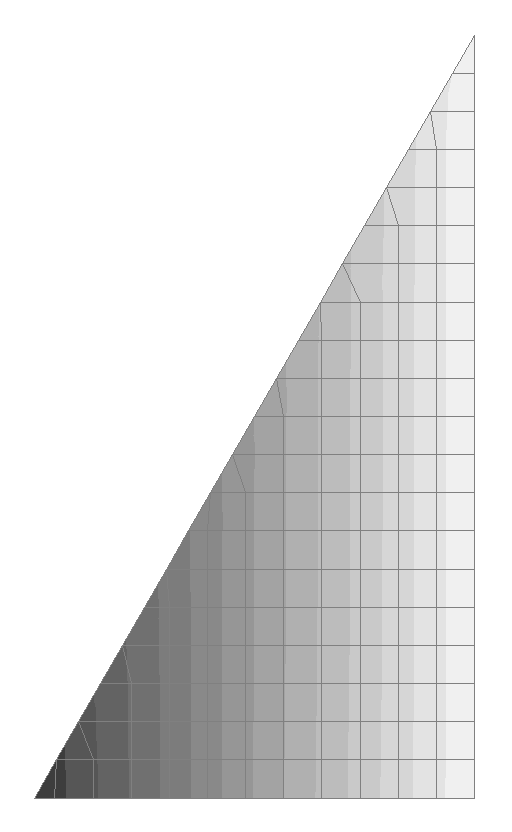

Значения напряжений τxy (кН/м2)
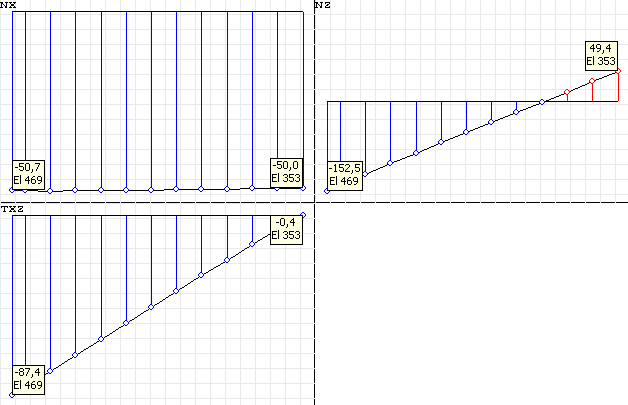
Значения напряжений σx, σy, τxy (кН/м2) в горизонтальном сечении плотины, расположенном на глубине y0 = 5.0 м от вершины плотины
Сравнение решений:
Компоненты тензора напряжений в декартовых координатах σx, σy, τxy в горизонтальном сечении плотины, расположенном на глубине y0 = 5.0 м от вершины плотины.
|
Параметр |
На наклонной грани плотины (x = y0·tgβ = 2.8868 м) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
σx (кН/м2) |
-50.00 |
-50.69 |
1.38 |
|
σy (кН/м2) |
-150.00 |
-152.55 |
1.70 |
|
τxy (кН/м2) |
-86.60 |
-87.42 |
0.95 |
|
Параметр |
На вертикальной грани плотины (x = 0.0000 м) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
σx (кН/м2) |
-50.00 |
-50.00 |
0.00 |
|
σy (кН/м2) |
50.00 |
49.43 |
1.14 |
|
τxy (кН/м2) |
0.00 |
-0.43 |
- |
Замечания: При аналитическом решении напряжения σx, σy, τxy в теле плотины от воздействия собственного веса и гидростатического давления определяются по следующим формулам (В.И. Самуль, Основы теории упругости и пластичности. — Москва: Высшая школа, 1982, стр. 77):
\[ \sigma_{x} =-\gamma \cdot y; \quad \sigma_{y} =\left( {\frac{\gamma_{1} }{tg\beta }-\frac{2\cdot \gamma }{tg^{3}\beta }} \right)\cdot x+\left( {\frac{\gamma }{tg^{2}\beta }-\gamma _{1} } \right)\cdot y; \quad \tau_{xy} =-\frac{\gamma \cdot x}{tg^{2}\beta }. \]
