Действие на плоскость сосредоточенного момента и сосредоточенной силы
Цель: Определение напряженного состояния плоскости единичной толщины в полярных координатах от воздействия сосредоточенного момента и сосредоточенной силы.
Файл с исходными данными: 4_26.spr
Формулировка задачи: В точке начала координат плоскости, толщина которой равна единице, приложены сосредоточенный момент M и сосредоточенная сила P1, действующая по оси Ox1. Определить компоненты тензора напряжений в полярных координатах σrr, σθθ, σrθ на различных радиальных расстояниях r от точки начала координат плоскости при угле наклона к оси Ox1 θ = 0º.
Ссылки: С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979.
Исходные данные:
| E = 3.0·107 кПа | - модуль упругости; |
| ν = 0.2 | - коэффициент Пуассона; |
| h = 1.0 м | - толщина плоскости; |
| R = 10.0 м | - радиус, ограничивающий область плоскости по закрепленной кромке; |
| M = 100.0 кН·м | - сосредоточенный момент, действующий в плоскости; |
| P1 = 100.0 кН | - сосредоточенная сила, действующая в плоскости по оси OX1. |
| P2 = 0.0 кН | - сосредоточенная сила, действующая в плоскости по оси OX2. |
Конечноэлементная модель: Расчетная схема – типа плоская рама, элементы пластины – 972 восьмиузловых элемента типа 30. Сетка конечных элементов разбита в радиальном направлении от r = 0.00 м до r = 0.50 м с шагом 0.05 м, от r = 0.50 м до r = 1.00 м с шагом 0.10 м, от r = 1.00 м до r = 5.00 м с шагом 0.50 м, от r = 5.00 м до r = 10.00 м с шагом 1.00 м и в тангенциальном направлении с шагом 10º. Направление выдачи внутренних усилий – радиально-тангенциальное. На цилиндрической поверхности малого радиуса a в окрестности точки приложения сосредоточенного момента M и сосредоточенной силы P1 эти усилия не могут быть представлены как равнодействующие напряжений, распределенных по законам аналитического решения, приведенного ниже. Ввиду этого, область плоскости, ограниченная этой цилиндрической поверхностью, моделируется твердым телом с ведущим узлом в точке приложения сосредоточенных усилий и ведомыми узлами на радиальном расстоянии a = 0.05 м от нее (тип элемента – 100). Для исключения влияния граничных условий на точность решения радиальное расстояние до закрепленной кромки плоскости принято равным R = 10.0 м. Количество узлов в расчетной схеме – 2989.
Результаты решения в SCAD
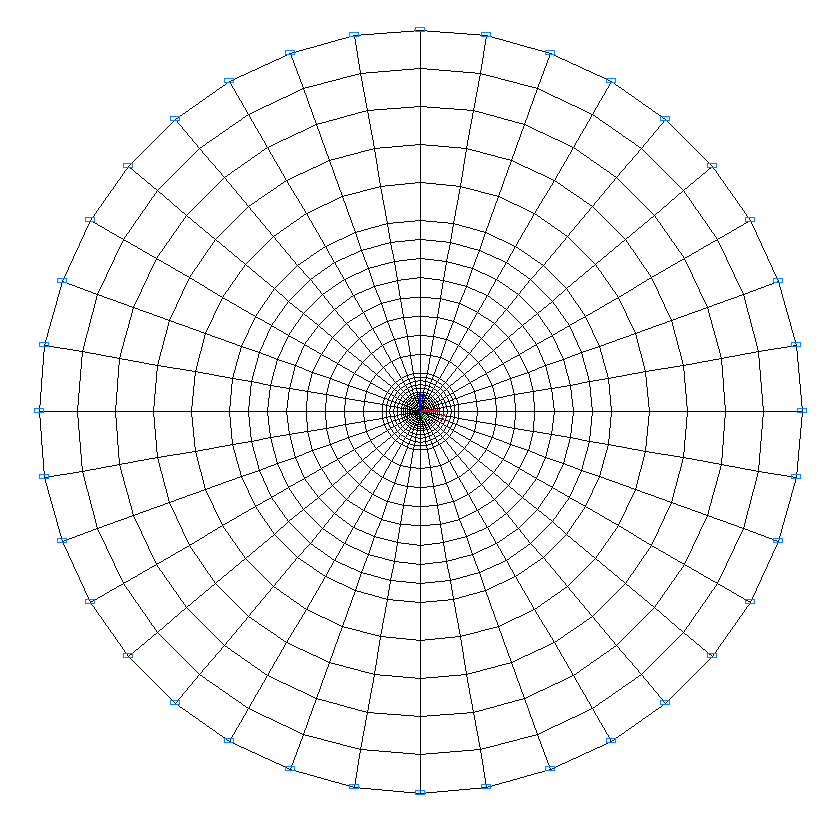
Расчетная схема
Значения напряжений σrr (кН/м2) при воздействии сосредоточенного момента M
Значения напряжений σθθ (кН/м2) при воздействии сосредоточенного момента M
Значения напряжений σrθ (кН/м2) при воздействии сосредоточенного момента M
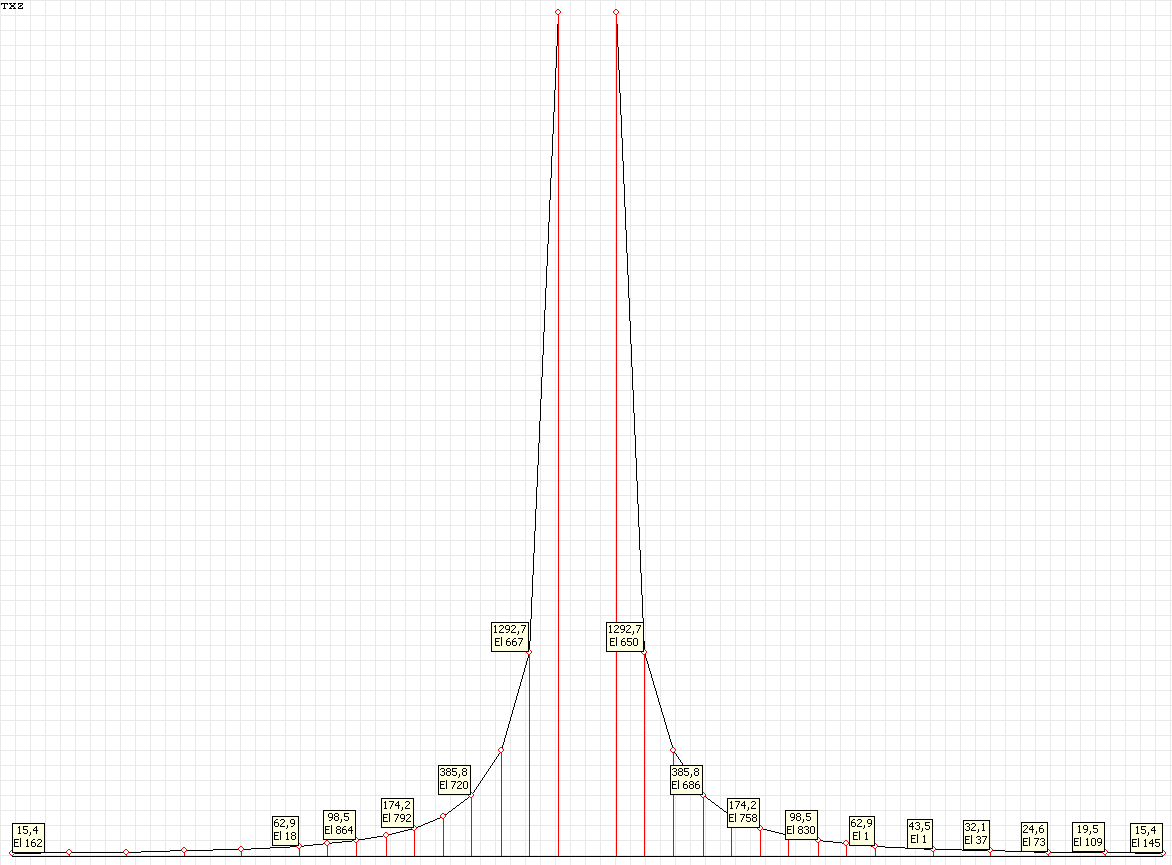
Эпюра напряжений σrθ (кН/м2) при воздействии сосредоточенного момента M для угла наклона к оси OX1 θ = 0º

Значения напряжений σrr (кН/м2) при воздействии сосредоточенной силы P1
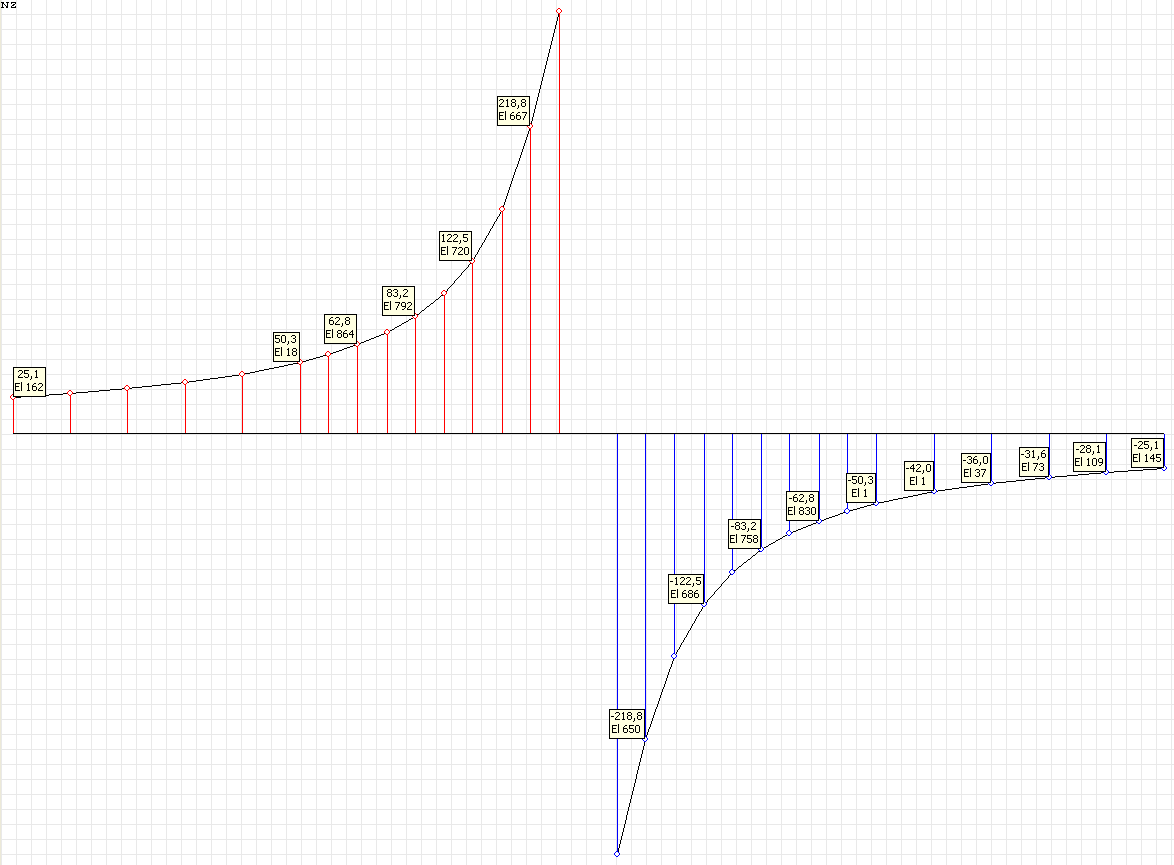
Эпюра напряжений σrr (кН/м2) при воздействии сосредоточенной силы P1 для угла наклона к оси Ox1 θ = 0º
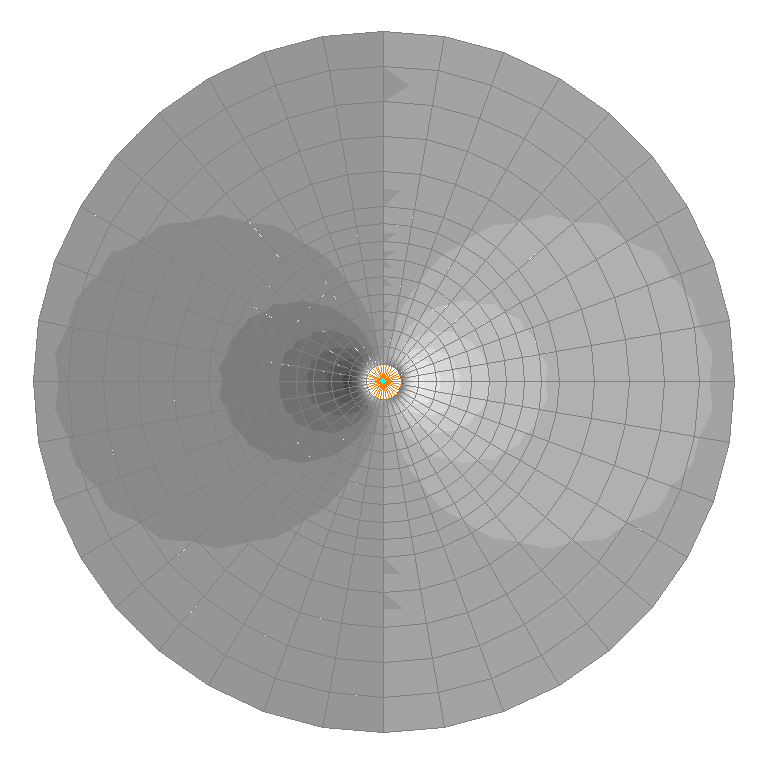
Значения напряжений σθθ (кН/м2) при воздействии сосредоточенной силы P1
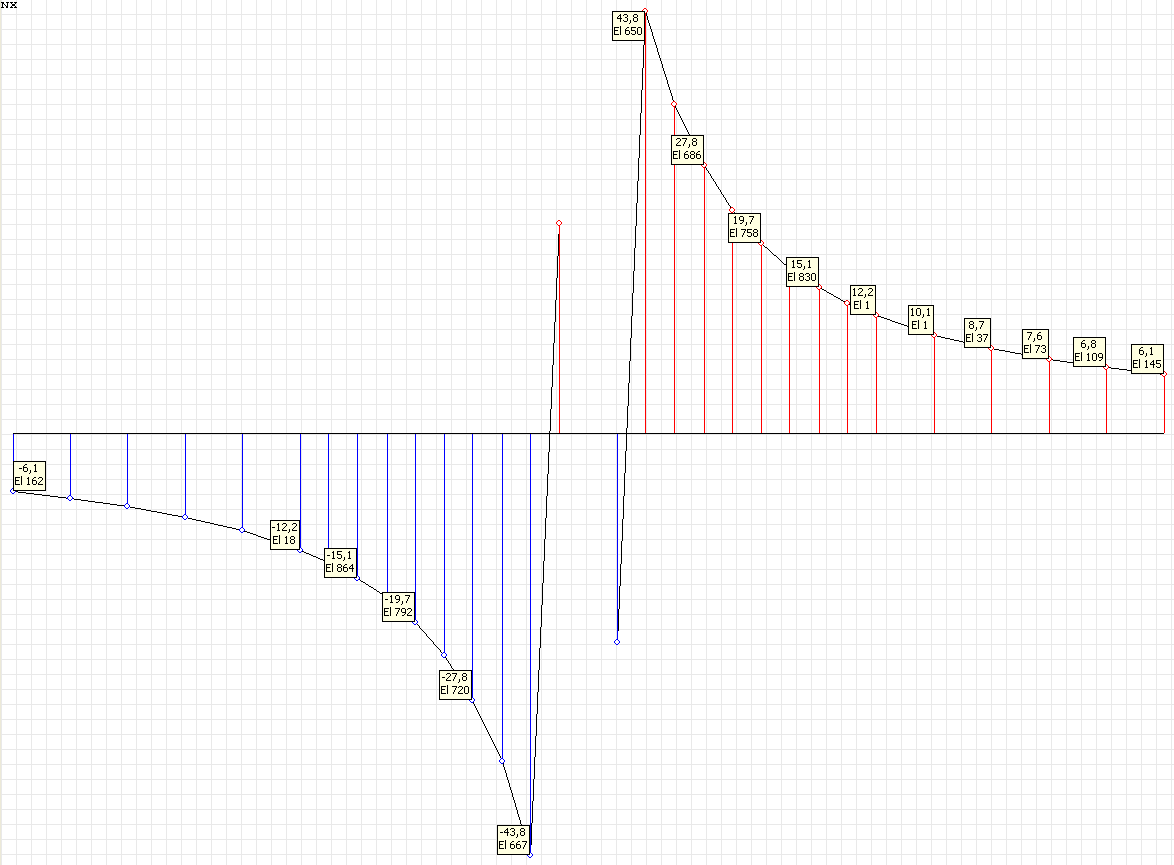
Эпюра напряжений σθθ (кН/м2) при воздействии сосредоточенной силы P1 для угла наклона к оси Ox1 θ = 0º
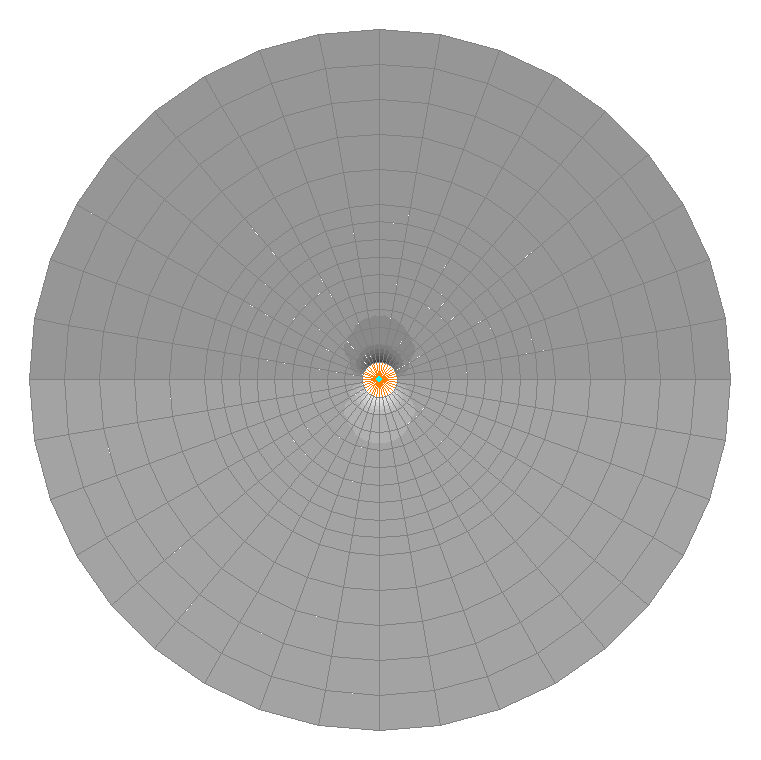
Значения напряжений σrθ (кН/м2) при воздействии сосредоточенной силы P1
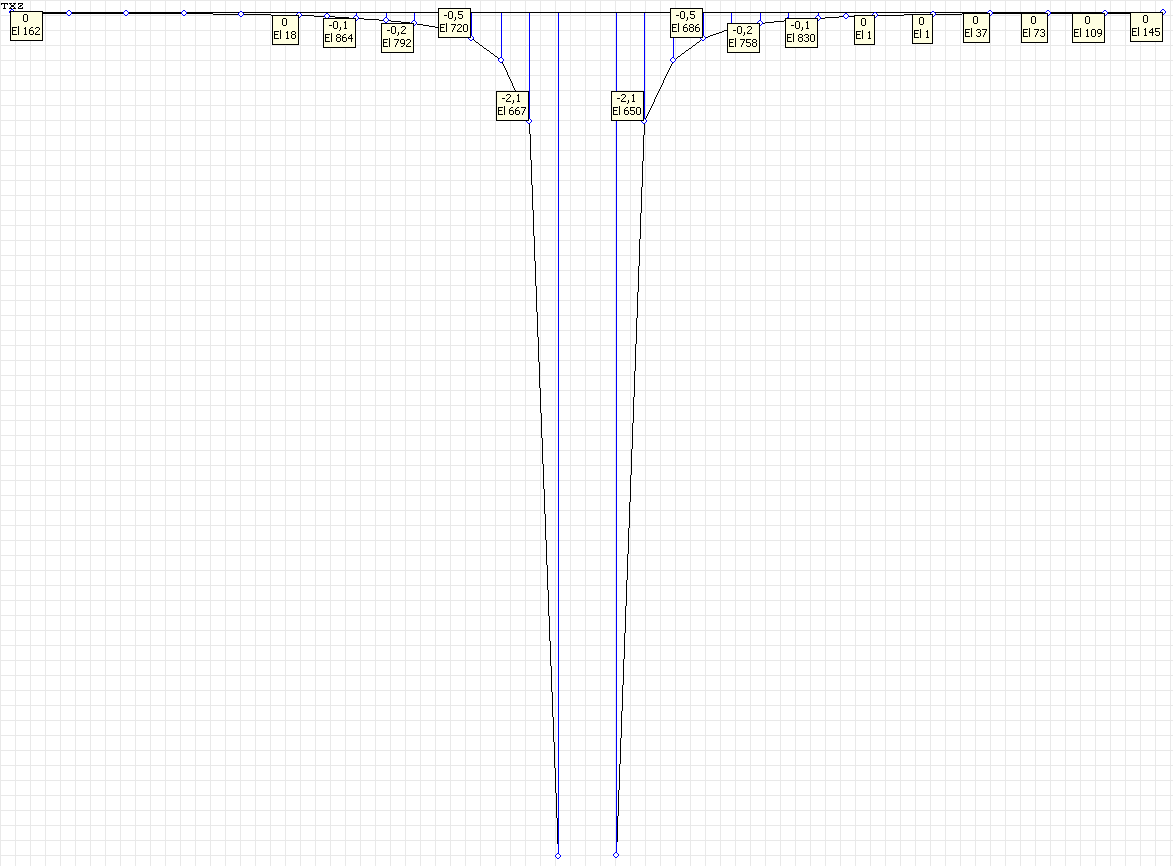
Эпюра напряжений σrθ (кН/м2) при воздействии сосредоточенной силы P1 для угла наклона к оси Ox1 θ = 0º
Сравнение решений:
Компоненты тензора напряжений для угла наклона к оси Ox1 θ = 0º при воздействии сосредоточенного момента M
|
Радиус r (м) |
Напряжения σrr (кН/м2) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
0.2 |
0.00 |
0.00 |
- |
|
0.3 |
0.00 |
0.00 |
- |
|
0.4 |
0.00 |
0.00 |
- |
|
0.5 |
0.00 |
0.00 |
- |
|
1.0 |
0.00 |
0.00 |
- |
|
1.5 |
0.00 |
0.00 |
- |
|
2.0 |
0.00 |
0.00 |
- |
|
2.5 |
0.00 |
0.00 |
- |
|
3.0 |
0.00 |
0.00 |
- |
|
Радиус r (м) |
Напряжения σθθ (кН/м2) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
0.2 |
0.00 |
0.00 |
- |
|
0.3 |
0.00 |
0.00 |
- |
|
0.4 |
0.00 |
0.00 |
- |
|
0.5 |
0.00 |
0.00 |
- |
|
1.0 |
0.00 |
0.00 |
- |
|
1.5 |
0.00 |
0.00 |
- |
|
2.0 |
0.00 |
0.00 |
- |
|
2.5 |
0.00 |
0.00 |
- |
|
3.0 |
0.00 |
0.00 |
- |
|
Радиус r (м) |
Напряжения σrθ (кН/м2) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
0.2 |
397.89 |
385.79 |
3.04 |
|
0.3 |
176.84 |
174.22 |
1.48 |
|
0.4 |
99.47 |
98.49 |
0.99 |
|
0.5 |
63.66 |
62.93 |
1.15 |
|
1.0 |
15.92 |
15.43 |
3.08 |
|
1.5 |
7.07 |
6.67 |
5.65 |
|
2.0 |
3.98 |
3.86 |
3.02 |
|
2.5 |
2.55 |
2.50 |
1.96 |
|
3.0 |
1.77 |
1.74 |
1.69 |
Компоненты тензора напряжений для угла наклона к оси Ox1 θ = 0º при воздействии сосредоточенной силы P1.
|
Радиус r (м) |
Напряжения σrr (кН/м2) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
0.2 |
-127.32 |
-122.67 |
3.65 |
|
0.3 |
-84.88 |
-83.26 |
1.91 |
|
0.4 |
-63.66 |
-62.84 |
1.29 |
|
0.5 |
-50.93 |
-50.36 |
1.12 |
|
1.0 |
-25.46 |
-25.08 |
1.49 |
|
1.5 |
-16.98 |
-16.65 |
1.94 |
|
2.0 |
-12.73 |
-12.61 |
0.94 |
|
2.5 |
-10.19 |
-10.15 |
0.39 |
|
3.0 |
-8.49 |
-8.50 |
0.12 |
|
Радиус r (м) |
Напряжения σθθ (кН/м2) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
0.2 |
31.83 |
27.80 |
12.66 |
|
0.3 |
21.22 |
19.69 |
7.21 |
|
0.4 |
15.92 |
15.08 |
5.28 |
|
0.5 |
12.73 |
12.16 |
4.48 |
|
1.0 |
6.37 |
6.09 |
4.40 |
|
1.5 |
4.24 |
3.96 |
6.60 |
|
2.0 |
3.18 |
2.92 |
8.18 |
|
2.5 |
2.55 |
2.27 |
10.98 |
|
3.0 |
2.12 |
1.82 |
14.15 |
|
Радиус r (м) |
Напряжения σrθ (кН/м2) |
||
|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
|
|
0.2 |
0.00 |
0.00 |
- |
|
0.3 |
0.00 |
0.00 |
- |
|
0.4 |
0.00 |
0.00 |
- |
|
0.5 |
0.00 |
0.00 |
- |
|
1.0 |
0.00 |
0.00 |
- |
|
1.5 |
0.00 |
0.00 |
- |
|
2.0 |
0.00 |
0.00 |
- |
|
2.5 |
0.00 |
0.00 |
- |
|
3.0 |
0.00 |
0.00 |
- |
Замечания:
1. При аналитическом решении напряжения σrr, σθθ, σrθ в плоскости при воздействии сосредоточенного момента определяются по следующим формулам (С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979, стр. 299):
\[ \sigma_{rr} =0; \quad \sigma_{\theta \theta } =0; \quad \sigma_{r\theta } =-\frac{M}{2\cdot \pi \cdot r^{2}}. \]
При аналитическом решении напряжения σrr, σθθ, σrθ в плоскости при воздействии сосредоточенной силы определяются по следующим формулам (С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979, стр. 300):
\[ \sigma_{rr} =-\frac{3+\nu }{4\cdot \pi \cdot r}\cdot \left( {P_{1} \cdot \cos \theta +P_{2} \cdot \sin \theta } \right); \] \[ \sigma_{\theta \theta } =\frac{1-\nu }{4\cdot \pi \cdot r}\cdot \left( {P_{1} \cdot \cos \theta +P_{2} \cdot \sin \theta } \right); \] \[ \sigma_{r\theta } =\frac{1-\nu }{4\cdot \pi \cdot r}\cdot \left( {P_{1} \cdot \sin \theta -P_{2} \cdot \cos \theta } \right). \]
2. Средствами SCAD невозможно точное моделирование рассмотренной в источнике задачи, поскольку рассматривается бесконечная плоскость и, кроме того, решение имеет сингулярность. Поэтому в матрице верификации приведены отклонения от теоретического решения в точке, расположенной на расстоянии 1,5 м от начала координат.
