Изгиб кривого бруса узкого прямоугольного сечения силой, приложенной к незакрепленному концу (задача Головина)

Цель: Определение напряженного состояния кривого бруса узкого прямоугольного сечения при изгибе сосредоточенной силой, приложенной к его незакрепленному концу.

Файл с исходными данными: 4_21.spr

Формулировка задачи: К свободному концу консольного кривого бруса, толщина которого равна единице, приложена сила P, действующая параллельно его торцу в плоскости круговой оси бруса. Определить компоненты тензора напряжений в полярных координатах σ_rr, σ_θθ, σ_rθ для поперечного сечения бруса, расположенного под углом θ = 90º от торца свободного конца бруса (сечение n-n).

Ссылки: С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979.

Исходные данные:

E = 3.0·107 кПа	- модуль упругости;
μ = 0.2	- коэффициент Пуассона;
h = 1.0 м	- толщина бруса;
r1 = 5 м	- внутренний радиус бруса;
r2 = 15 м	- внешний радиус бруса;
P = 5.0 кН	- сосредоточенная сила, изгибающая брус (горизонтальная).

Связи: полное закрепление узлов защемленного торца бруса (сечение m-m)

Конечноэлементная модель: Расчетная  схема – система общего вида, элементы бруса – 300 восьмиузловых элементов типа 50. Сетка конечных элементов разбита с шагом 1.0 м в радиальном направлении и с шагом 9º в тангенциальном направлении. Направление выдачи внутренних усилий – радиально-тангенциальное. Ввиду того, что граничные условия на торцевой поверхности свободного конца кривого бруса (θ = 0º) в аналитическом решении заданы в интегральной форме, произведено их смягчение путем введения твердого тела (тип элемента – 100) , узлы которого расположены вдоль торцевой поверхности. Количество узлов в расчетной схеме – 981.

Результаты решения в SCAD

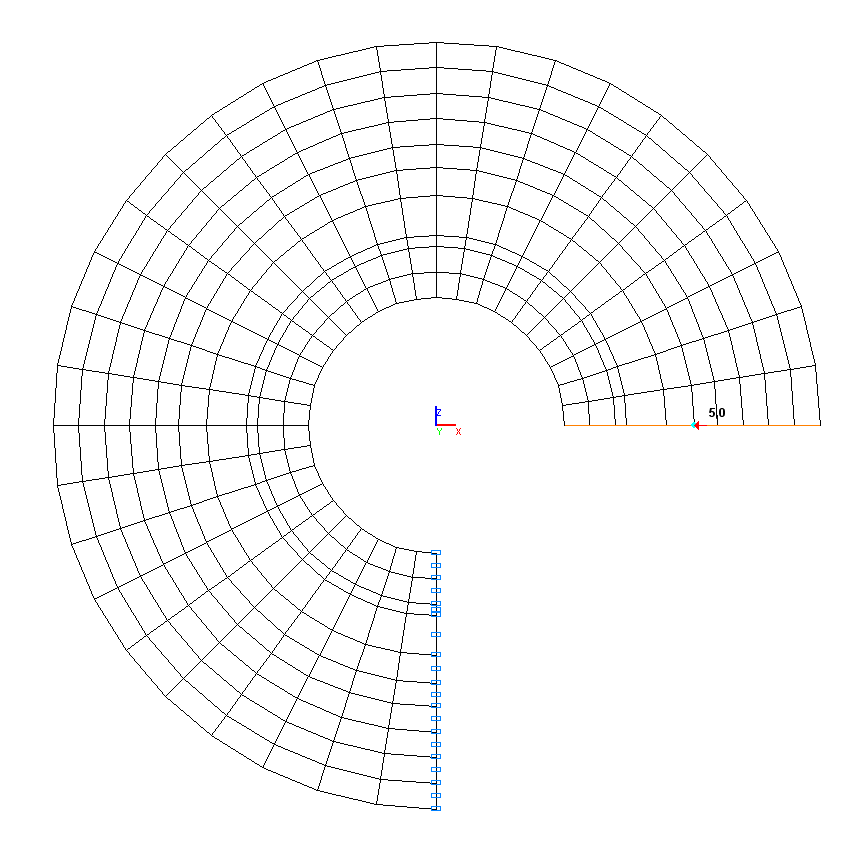
Расчетная схема

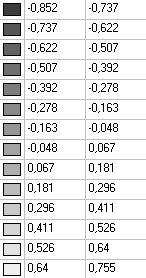
Значения напряжений σrr (кН/м²)

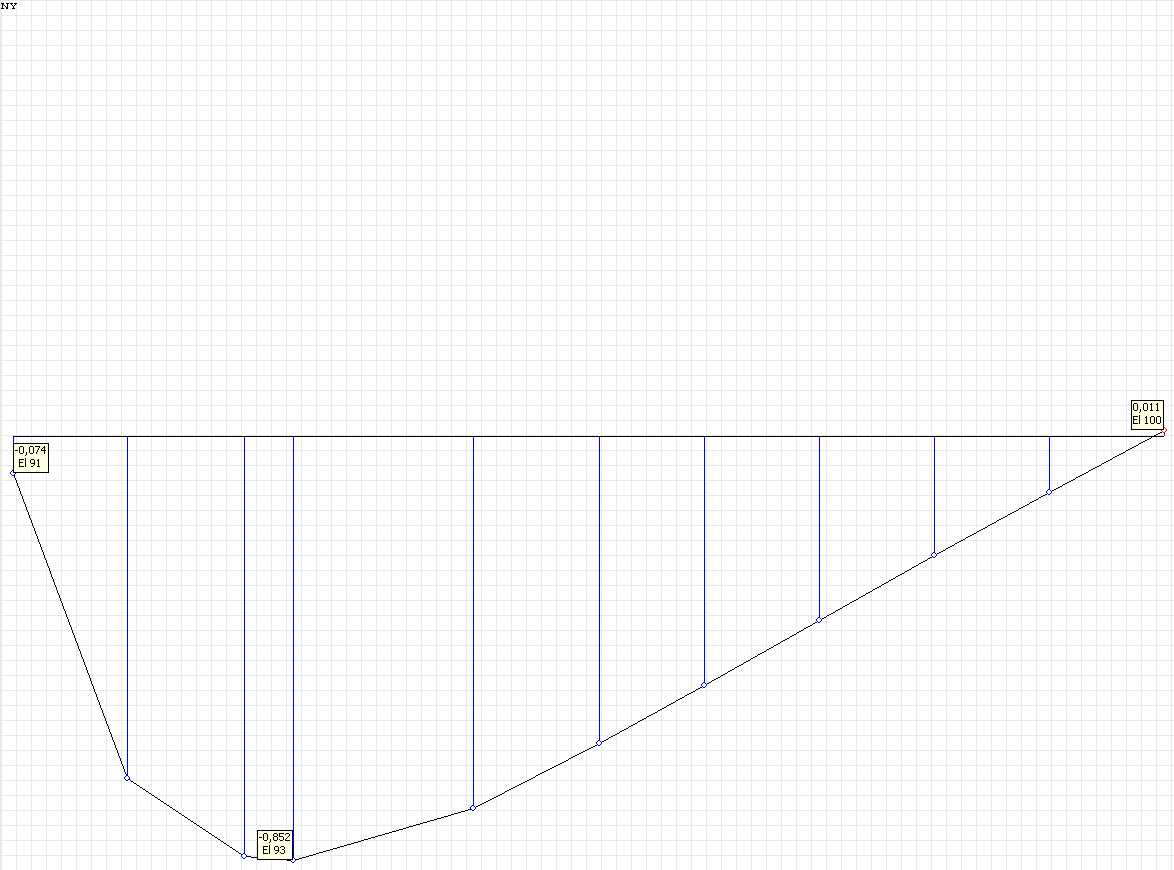
Эпюра напряжений σ_rr (кН/м²) для поперечного сечения бруса, расположенного под углом θ = 90º от торца свободного конца бруса (сечение n-n)

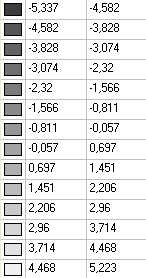
Значения напряжений σ_θθ (кН/м²)

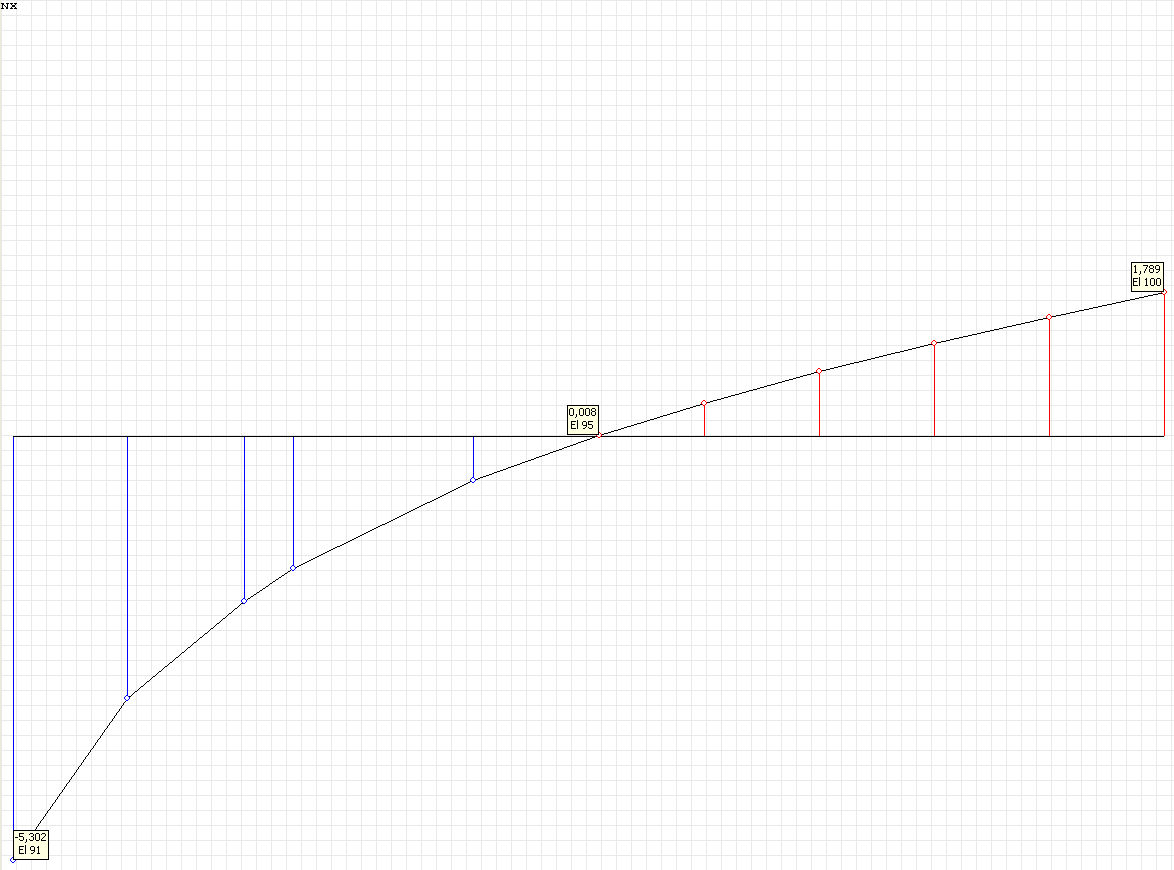
Эпюра напряжений σ_θθ (кН/м²) для поперечного сечения бруса, расположенного под углом θ = 90º от торца свободного конца бруса (сечение n-n)

Значения напряжений σ_rθ (кН/м²)

Сравнение решений:

	Напряжения σrr (кН/м2)			Напряжения σθθ (кН/м2)
	r = 5.0000 м	r = 7.4349 м	r = 15.0000 м	r = 5.0000 м	r = 10.0876 м	r = 15.0000 м
Теория	0.0000	-0.8375	0.0000	-5.3581	0.0000	1.7860
SCAD	-0.0744	-0.8515	0.0109	-5.3022	0.0078	1.7893
Отклонения, %	─	1.67	─	1.04	─	0.18

Замечания: При аналитическом решении напряжения σ_rr, σ_θθ, σ_rθ  в теле консольного кривого бруса от воздействия силы P на его свободном конце, направленной параллельно его торцу, определяются по следующим формулам (С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979, стр. 271):

\[ \sigma_{rr} =\frac{P}{K_{0} }\cdot \left( {r-\frac{r_{1}^{2}+r_{2} ^{2}}{r}+\frac{r_{1}^{2}\cdot r_{2}^{2}}{r^{3}}} \right)\cdot \sin \theta ; \] \[ \sigma_{\theta \theta } =\frac{P}{K_{0} }\cdot \left( {3\cdot r-\frac{r_{1} ^{2}+r_{2}^{2}}{r}-\frac{r_{1}^{2}\cdot r_{2}^{2}}{r^{3}}} \right)\cdot \sin \theta ; \] \[ \sigma_{rr} =-\frac{P}{K_{0} }\cdot \left( {r-\frac{r_{1}^{2}+r_{2} ^{2}}{r}+\frac{r_{1}^{2}\cdot r_{2}^{2}}{r^{3}}} \right)\cdot \cos \theta ; \] \[ K_{0} =r_{1}^{2}-r_{2}^{2}+\left( {r_{1}^{2}+r_{2}^{2}} \right)\cdot \ln \left( {r_{2} /r_{1} } \right). \]