Плоская шарнирно-стержневая система из элементов различного материала под действием изменения температуры
Цель: Определение напряженного состояния плоской шарнирно-стержневой системы из элементов различного материала от воздействия изменения температуры.
Формулировка задачи:
Три стержня плоской системы шарнирно сопряжены в общем узле (O) и шарнирно оперты в противоположных узлах (B, C, D). Опорные узлы расположены на одной горизонтальной прямой симметрично относительно вертикальной оси (OC), общий узел лежит на вертикальной оси. Вертикальный стержень (OC) выполнен из стали, наклонные стержни (OB, OD) выполнены из меди. Система подвергается воздействию от изменения температуры Δt относительно температуры сборки. Определить продольные усилия N в каждом стержне.
Ссылки: С.П. Тимошенко, Сопротивление материалов, том первый: Элементарная теория и задачи, Москва, Наука, 1965, стр. 34.
Исходные данные:
| Es = 2.0·106 кгс/см2 | - модуль упругости стали; |
| Eс = 1.0·106 кгс/см2 | - модуль упругости меди; |
| αs = 1.25·10-5 1/ ºC | - коэффициент линейного температурного расширения стали; |
| αc = 1.65·10-5 1/ ºC | - коэффициент линейного температурного расширения меди; |
| l = 100.0 см | - длина вертикального стержня; |
| φ = 45 º | - угол сопряжения наклонных стержней с вертикальным стержнем; |
| As = 5.0•5.0 см2 | - площадь поперечного сечения вертикального стального стержня; |
| Ac = 5.0•5.0 см2 | - площадь поперечного сечения наклонного медного стержня; |
| Δt = 50 ºC | - изменение температуры системы. |
Файл с исходными данными: T1_v11.3.spr
Конечноэлементная модель: Расчетная схема – плоская шарнирно-стержневая система, 3 элемента типа 1. Обеспечение граничных условий достигается за счет наложения связей в опорных узлах по направлениям степеней свободы X, Z. Воздействие от изменения температуры системы Δt относительно температуры сборки задается равномерным вдоль продольных осей всех стержневых элементов. Количество узлов в расчетной схеме 4.
Результаты решения в SCAD
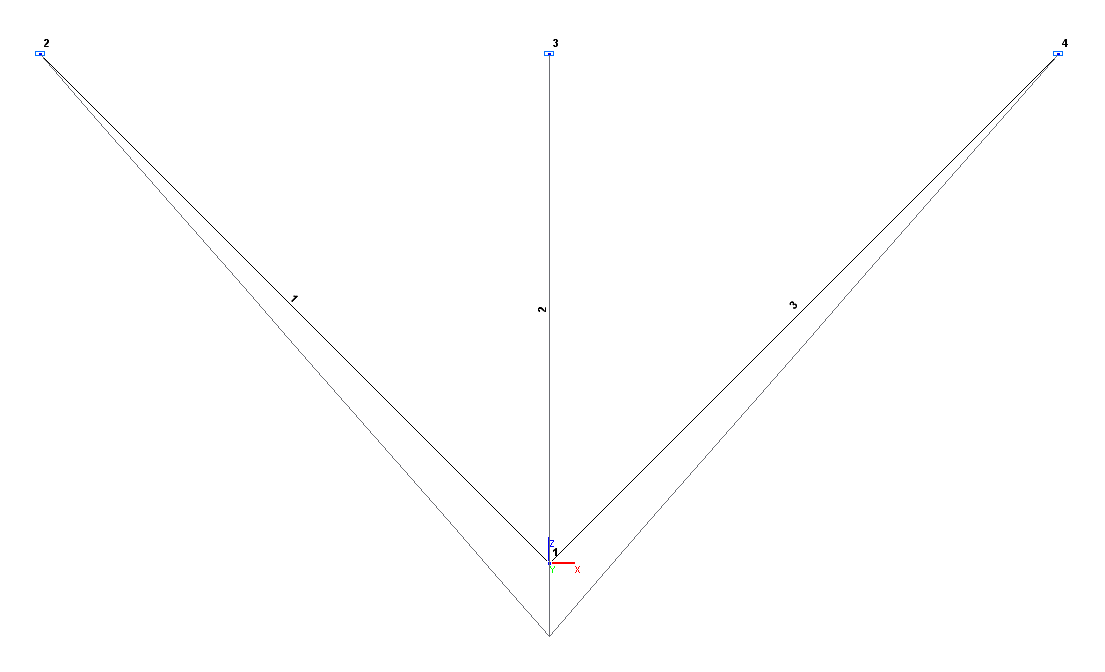
Расчетная и деформированная схемы
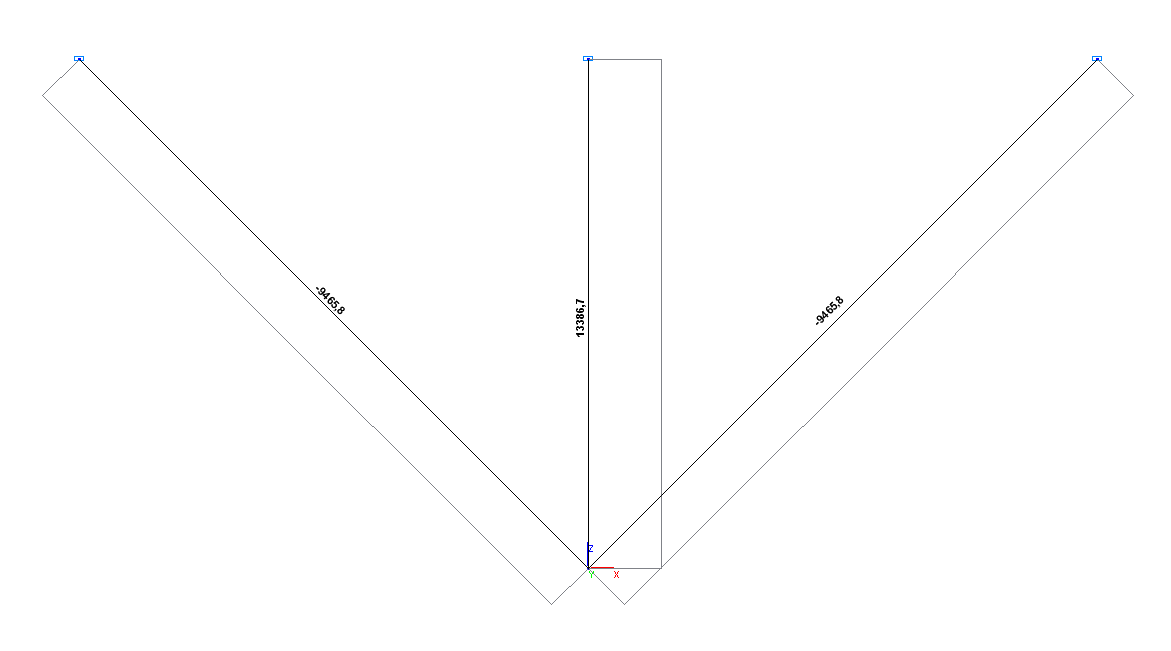
Эпюра продольных сил N (кгс)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Продольная сила N (стержень OC), кгс |
13386.7 |
13386.7 |
0.00 |
|
Продольная сила N (стержни OB и OD), кгс |
-9465.8 |
-9465.8 |
0.00 |
Замечания: При аналитическом решении продольные усилия N в стержнях системы определяются по следующим формулам:
\[ N_{OC} =\frac{\Delta t\cdot \left( {\frac{\alpha_{c} }{\cos^{2}\left( \phi \right)}-\alpha_{s} } \right)\cdot E_{s} \cdot A_{s} }{1+\frac{1}{2\cdot \cos^{3}\left( \phi \right)}\cdot \frac{E_{s} \cdot A_{s} }{E_{c} \cdot A_{c} }}; \]
\[N_{OB} =N_{OD} =-\frac{\Delta t\cdot \left( {\frac{\alpha_{c} }{\cos ^{2}\left( \phi \right)}-\alpha_{s} } \right)\cdot E_{s} \cdot A_{s} }{2\cdot \cos \left( \phi \right)+\frac{1}{\cos^{2}\left( \phi \right)}\cdot \frac{E_{s} \cdot A_{s} }{E_{c} \cdot A_{c} }}. \]
