Одностороннее растяжение пластины с малым круговым отверстием (задача Кирша)

Цель: Определение напряженного состояния пластины значительной ширины и единичной толщины с малым круговым отверстием в полярных координатах от воздействия одностороннего равномерного растяжения.

Файлы с исходными данными:

4.27_b_20_9_grad.spr	1 вариант расчетной схемы – крупная сетка КЭ
4.27_b_60_4.5_grad.spr	2 вариант расчетной схемы – мелкая сетка КЭ

 

Формулировка задачи: Квадратная пластина значительной ширины и единичной толщины с малым круговым отверстием радиуса a в ее центре подвергается одностороннему равномерному растяжению напряжениями σ в направлении оси x₁. Определить компоненты тензора напряжений в полярных координатах σ_rr, σ_θθ, σ_rθ на различных радиальных расстояниях r от точки начала координат при углах наклона к оси x₁ θ = 0º и θ = 90º.

Ссылки: С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979.

Исходные данные:

E = 3.0·107 кПа	- модуль упругости;
μ = 0.2	- коэффициент Пуассона;
h = 1.0 м	- толщина пластины;
a = 1.0 м	- радиус отверстия;
2·b = 20.0 м (60.0 м)	- ширина пластины;
σ = 100.0 кН/м	- растягивающее напряжение в направлении оси x1.

 

Конечноэлементная модель: Рассматривается два варианта расчетной схемы.

Вариант 1:

Расчетная  схема – типа плоская рама, ширина пластины 2·b = 20.0 м, элементы пластины – 1088 восьмиузловых элементов типа 30 и 32 шестиузловых элемента типа 25. Сетка конечных элементов разбита в радиальном направлении от r = 1.00 м до r = 2.00 м с шагом 0.10 м,  от r = 2.00 м до r = 10.00 м с шагом 0.50 м и в тангенциальном направлении с шагом 9º. Направление выдачи внутренних усилий – радиально-тангенциальное. Количество узлов в расчетной схеме – 3409.

Вариант 2:

Расчетная  схема – типа плоская рама, ширина пластины 2·b = 60.0 м, элементы пластины – 5024 восьмиузловых элементов типа 30 и 40 шестиузловых элементов типа 25. Сетка конечных элементов разбита в радиальном направлении от r = 1.00 м до r = 3.00 м с шагом 0.10 м,  от r = 3.00 м до r = 5.00 м с шагом 0.20 м, от r = 5.00 м до r = 9.00 м с шагом 0.40 м, от r = 9.00 м до r = 21.00 м с шагом 0.80 м, от r = 21.00 м до r = 29.00 м с шагом 1.60 м и в тангенциальном направлении с шагом 4.5º. Направление выдачи внутренних усилий – радиально-тангенциальное. Количество узлов в расчетной схеме – 15312.

 

Результаты решения в SCAD

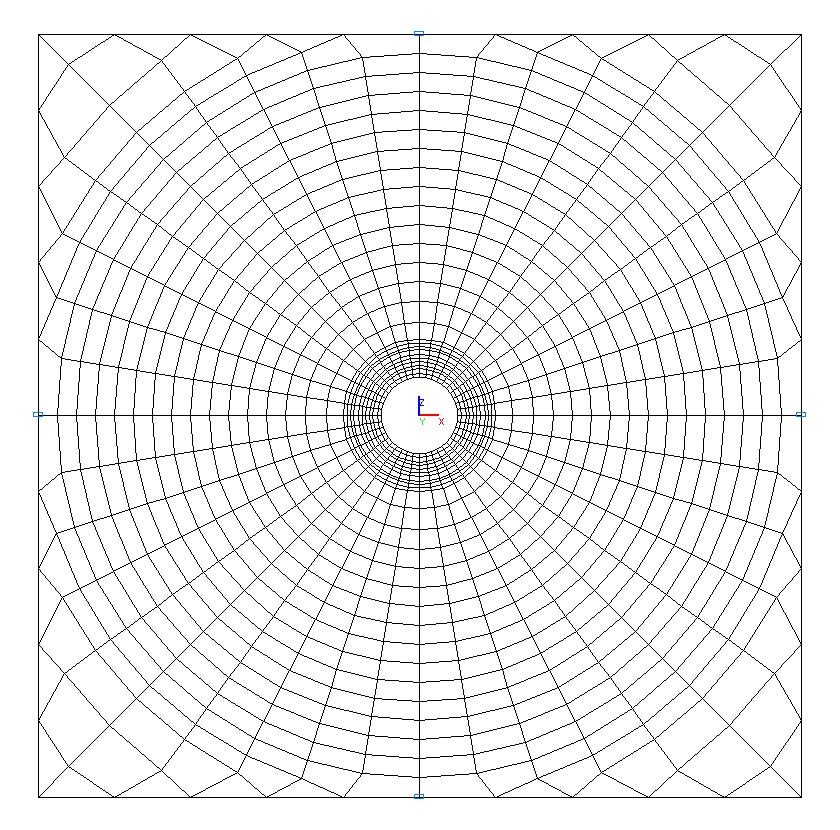
Расчетная схема. Вариант 1

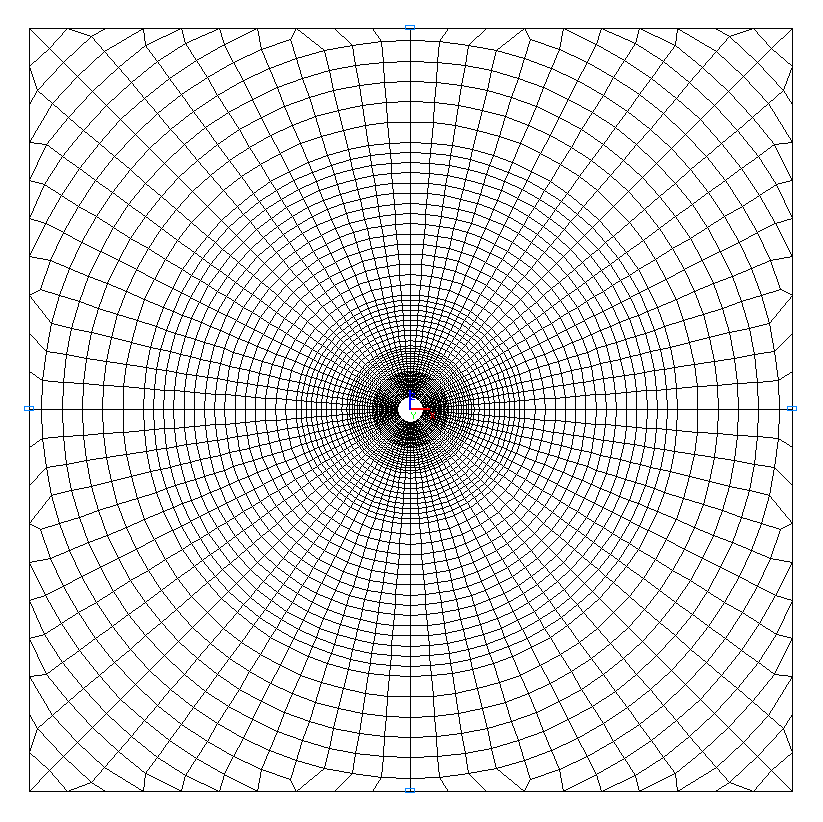
Расчетная схема. Вариант 2

 
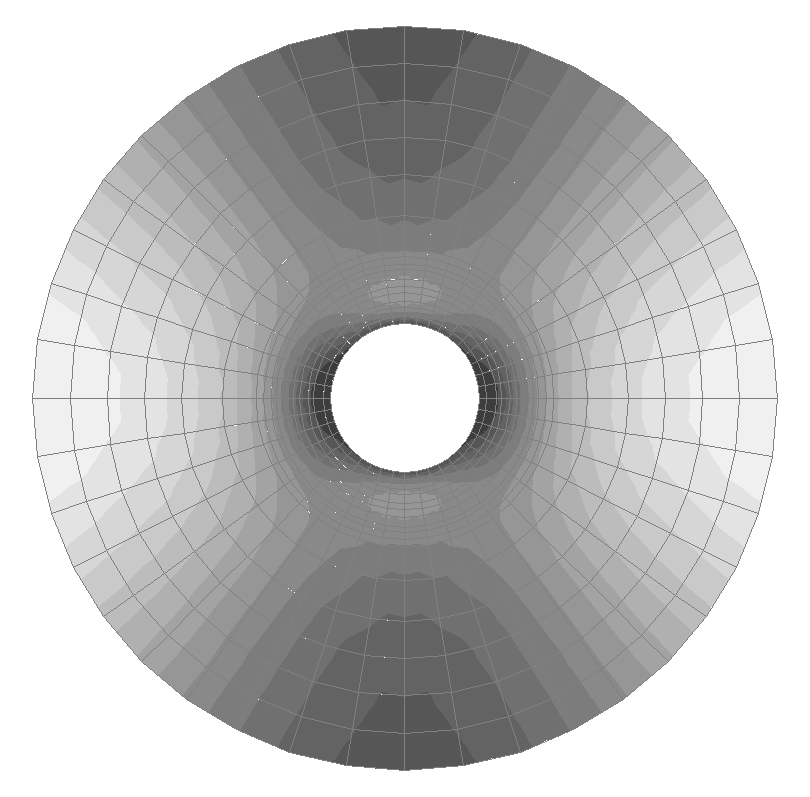
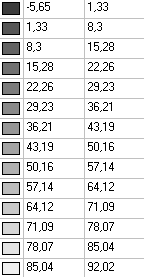
Значения напряжений σ_rr (кН/м²) для расчетной схемы по варианту 1

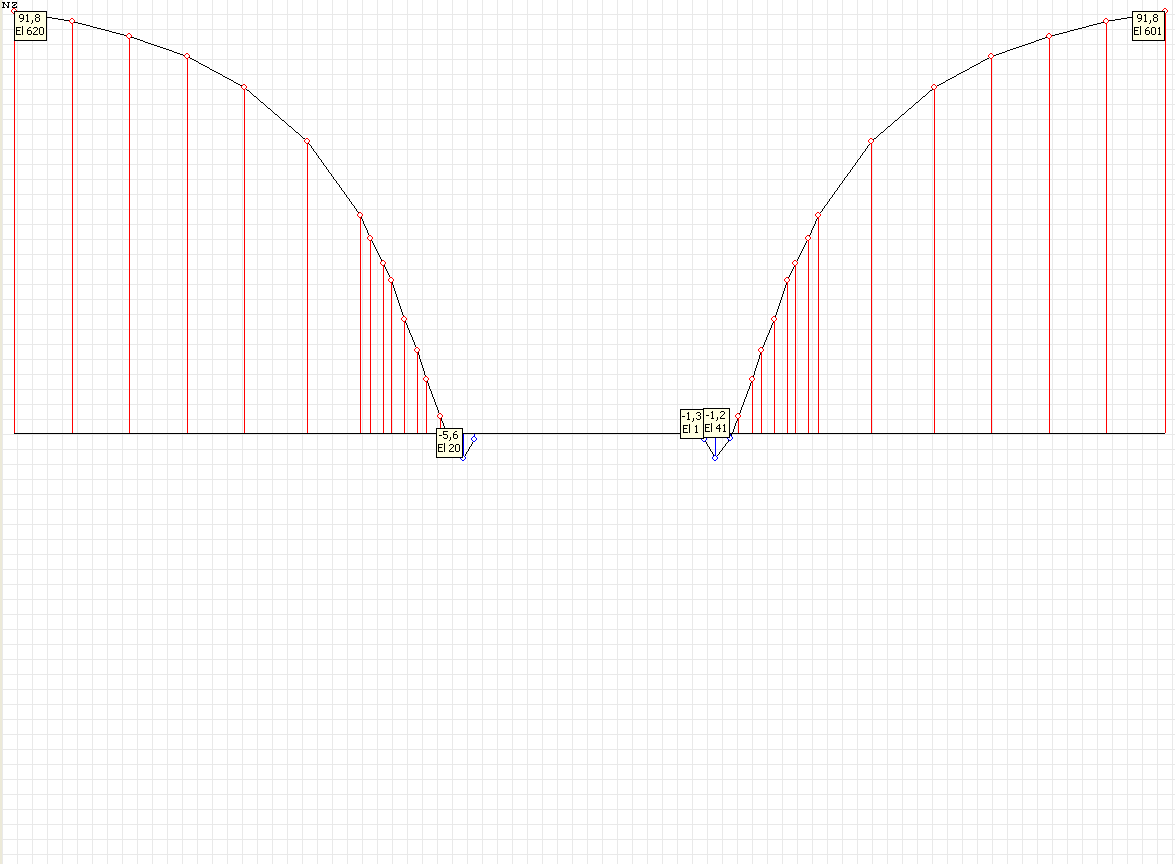
Эпюра напряжений σ_rr (кН/м²) при угле наклона к оси Ox₁ θ = 0º для расчетной схемы по варианту 1

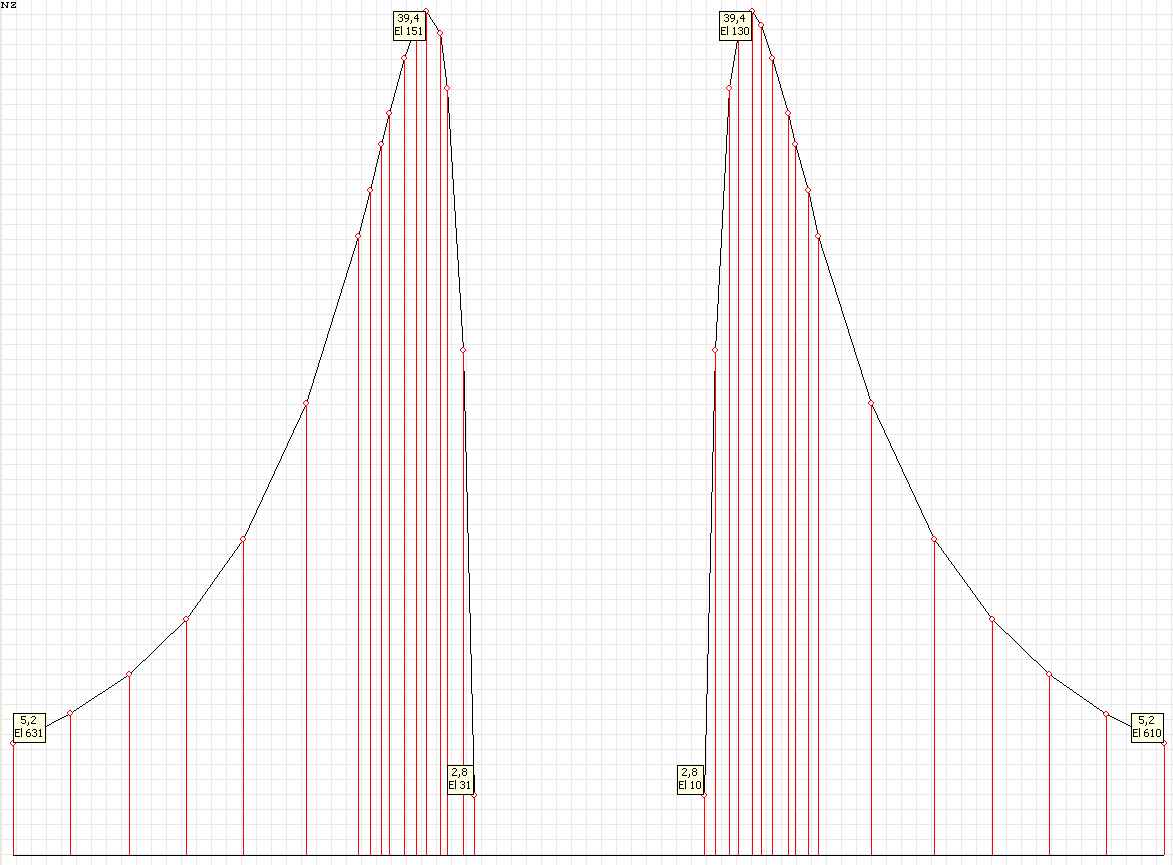
Эпюра напряжений σ_rr (кН/м²) при угле наклона к оси Ox₁ θ = 90º для расчетной схемы по варианту 1

Значения напряжений σ_rr (кН/м²) для расчетной схемы по варианту 2

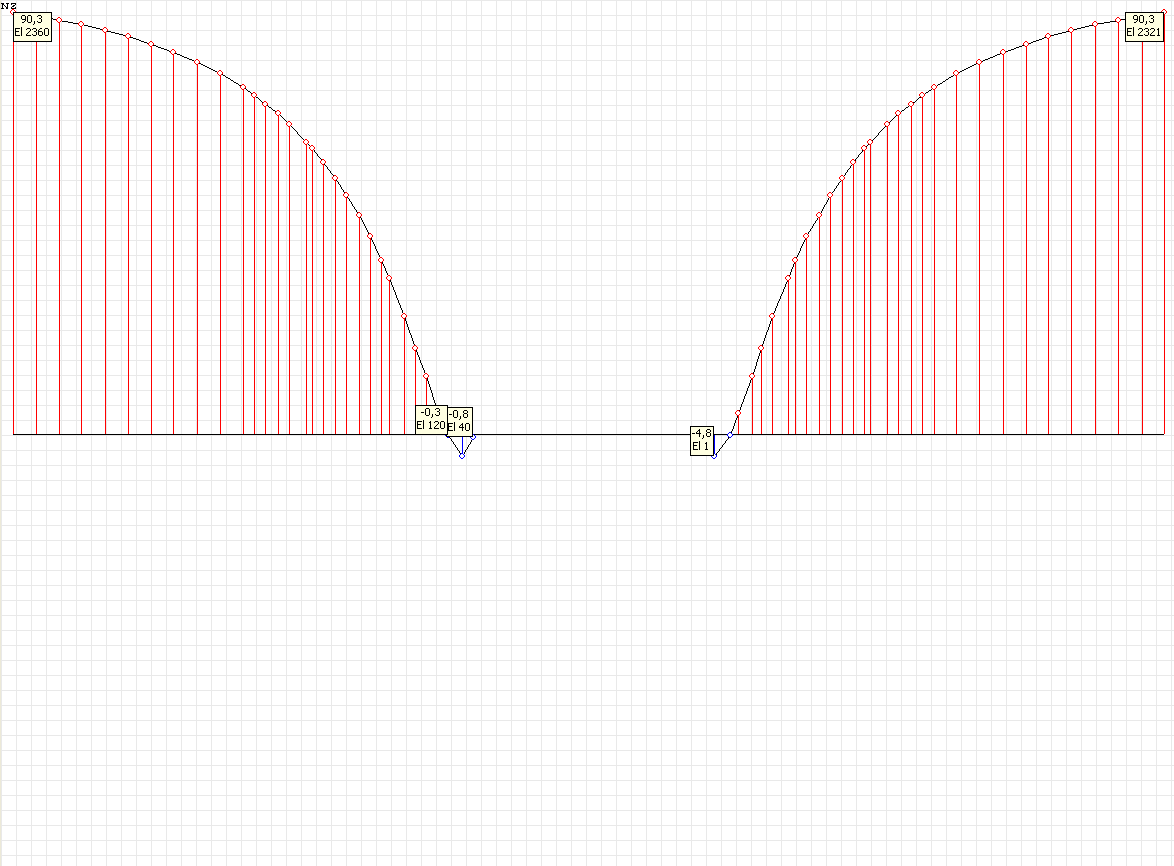
Эпюра напряжений σ_rr (кН/м²) при угле наклона к оси Ox₁ θ = 0º для расчетной схемы по варианту 2

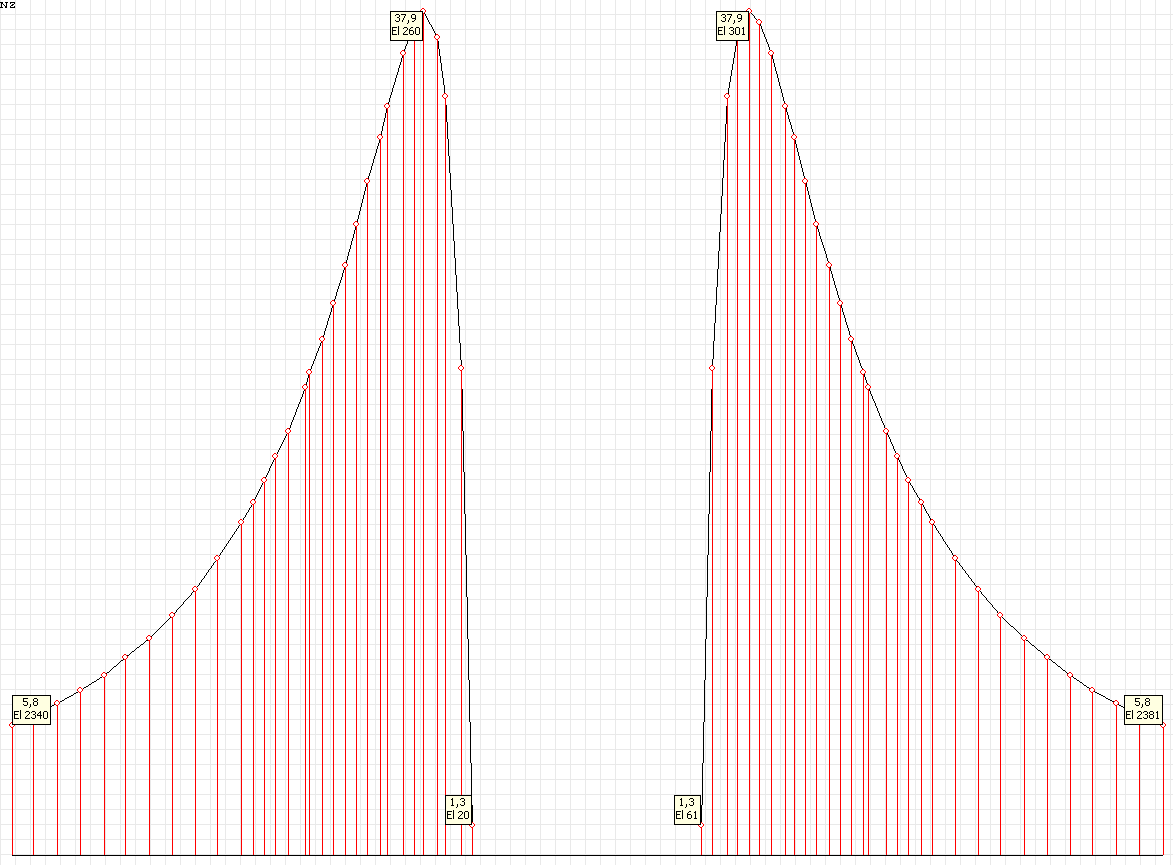
Эпюра напряжений σ_rr (кН/м²) при угле наклона к оси Ox₁ θ = 90º для расчетной схемы по варианту 2

Значения напряжений σ_θθ (кН/м²) для расчетной схемы по варианту 1

Эпюра напряжений σ_θθ (кН/м²) при угле наклона к оси Ox₁ θ = 0ºдля расчетной схемы по варианту 1

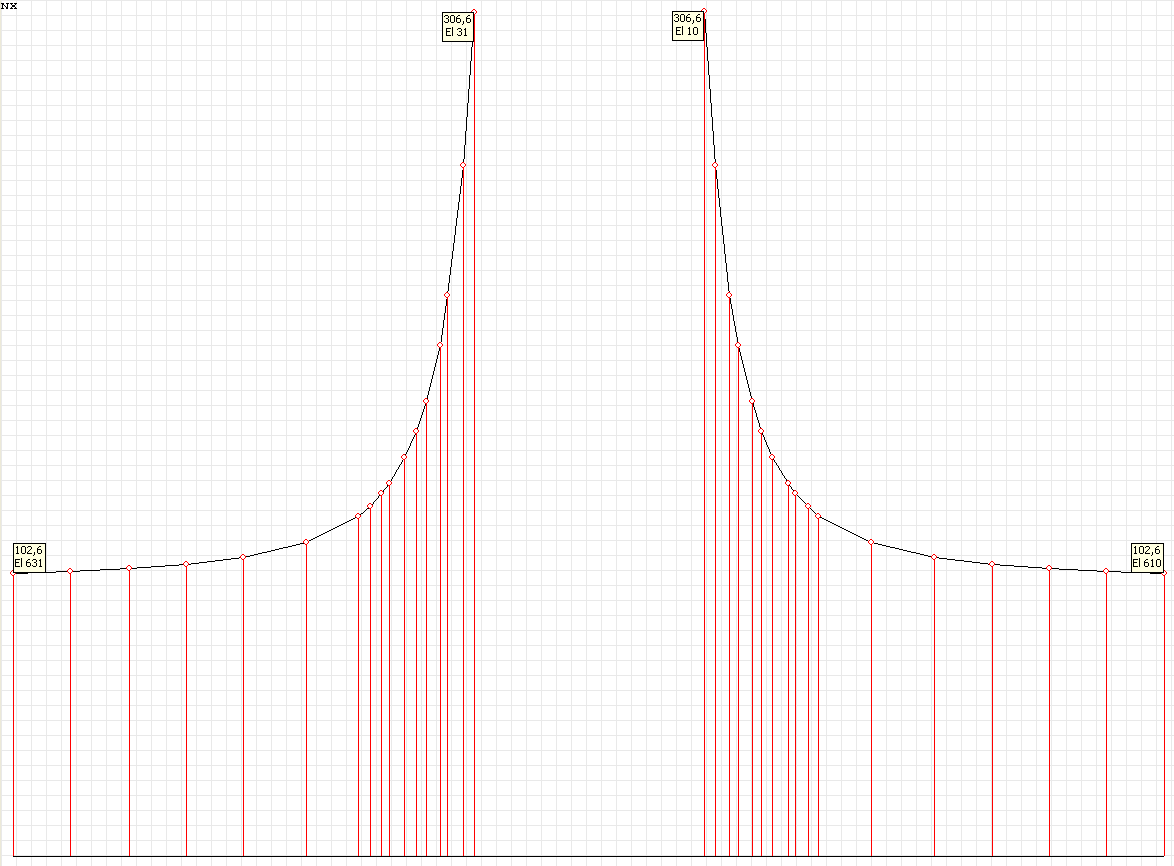
Эпюра напряжений σ_θθ (кН/м²) при угле наклона к оси Ox₁ θ = 90º для расчетной схемы по варианту 1

Значения напряжений σ_θθ (кН/м²) для расчетной схемы по варианту 2

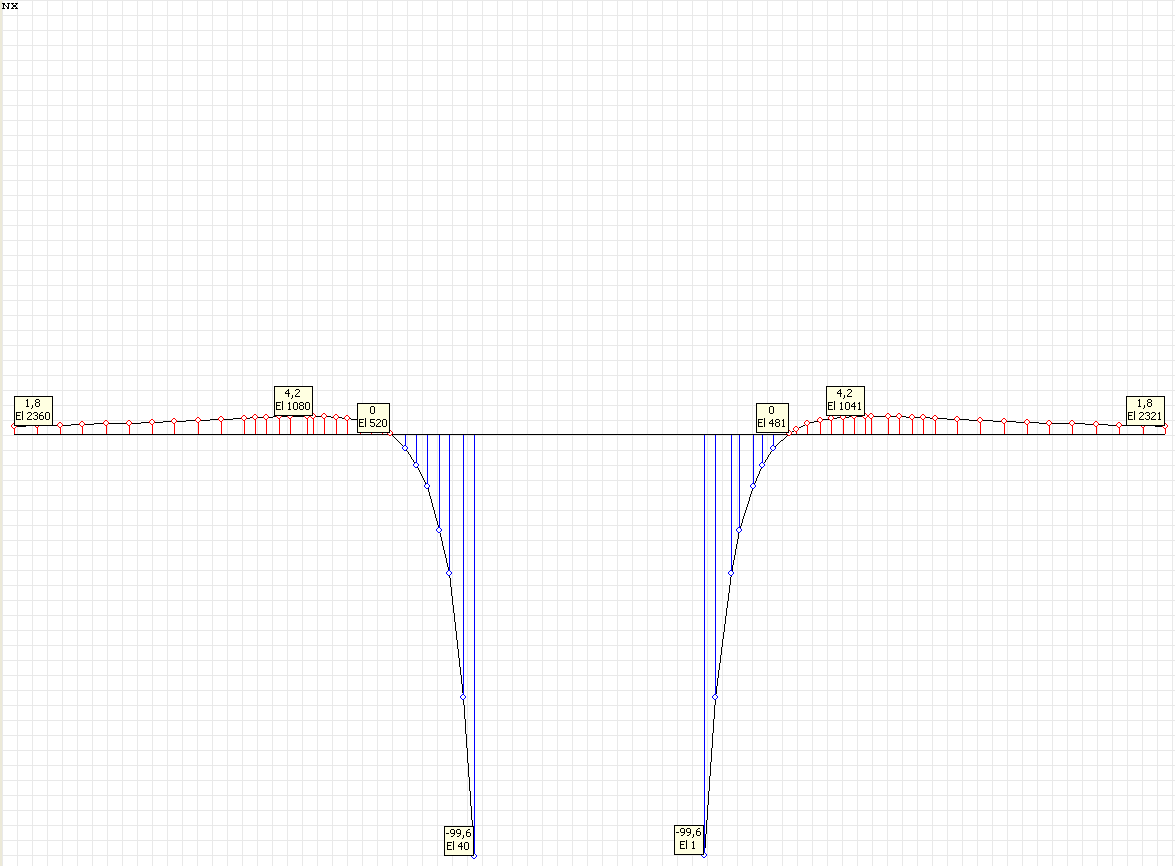
Эпюра напряжений σ_θθ (кН/м²) при угле наклона к оси Ox₁ θ = 0º для расчетной схемы по варианту 2

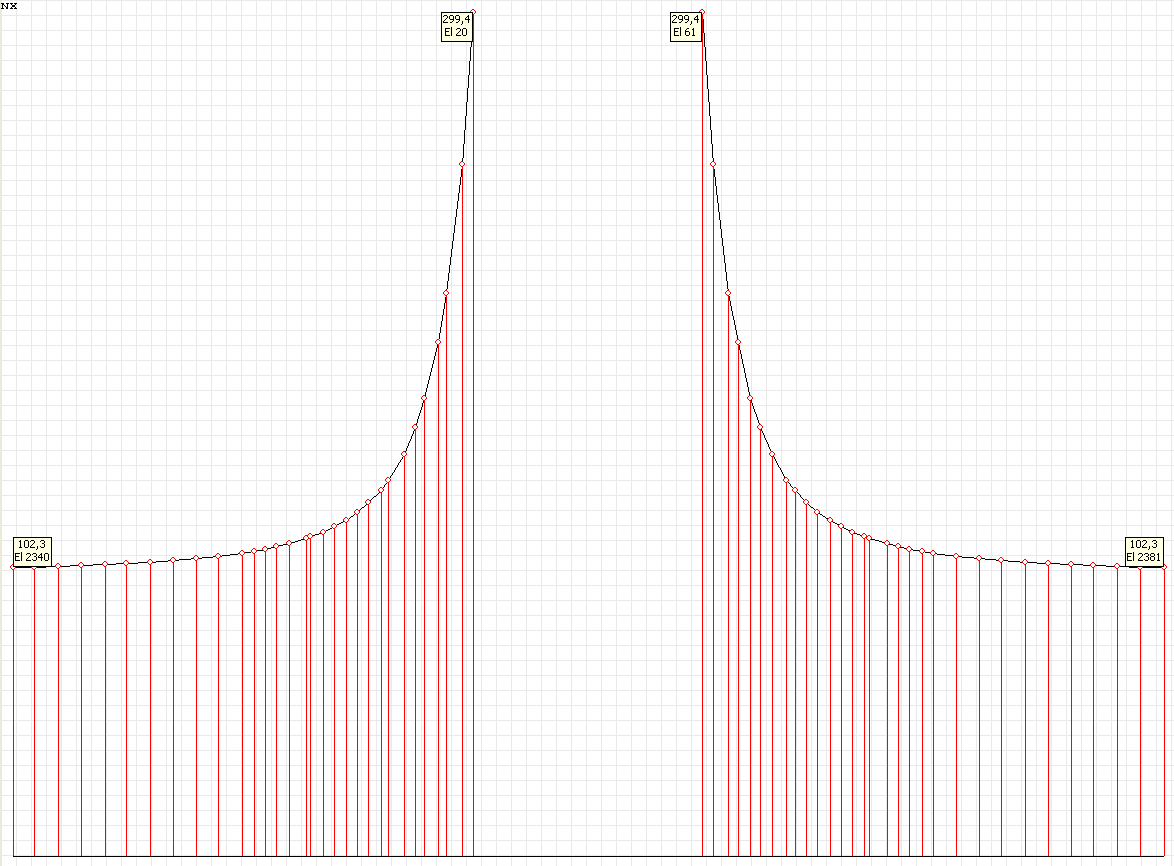
Эпюра напряжений σ_θθ (кН/м²) при угле наклона к оси Ox₁ θ = 90º для расчетной схемы по варианту 2

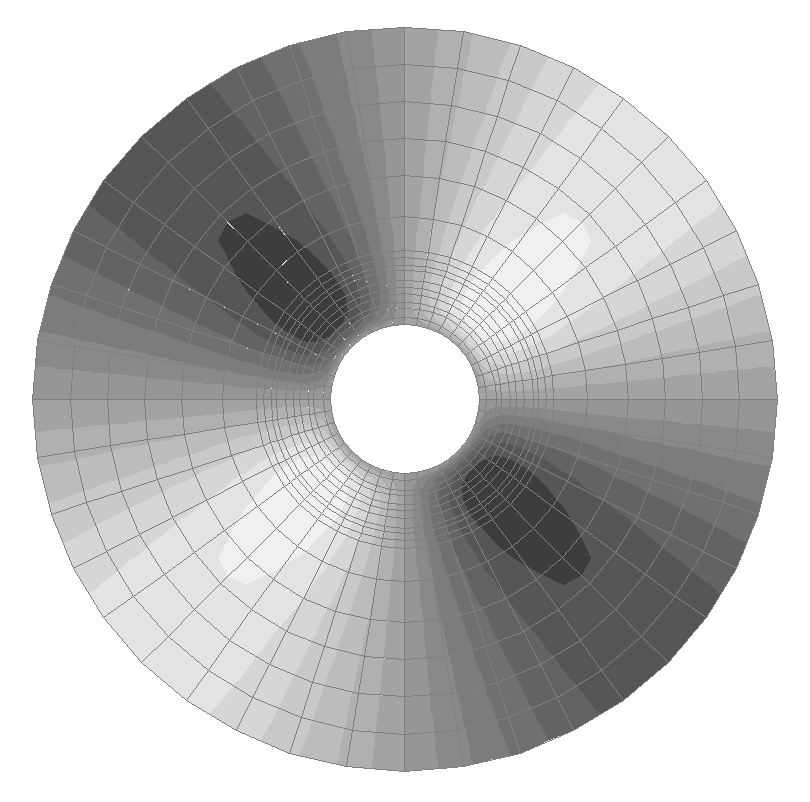
Значения напряжений σ_rθ (кН/м²) для расчетной схемы по варианту 1

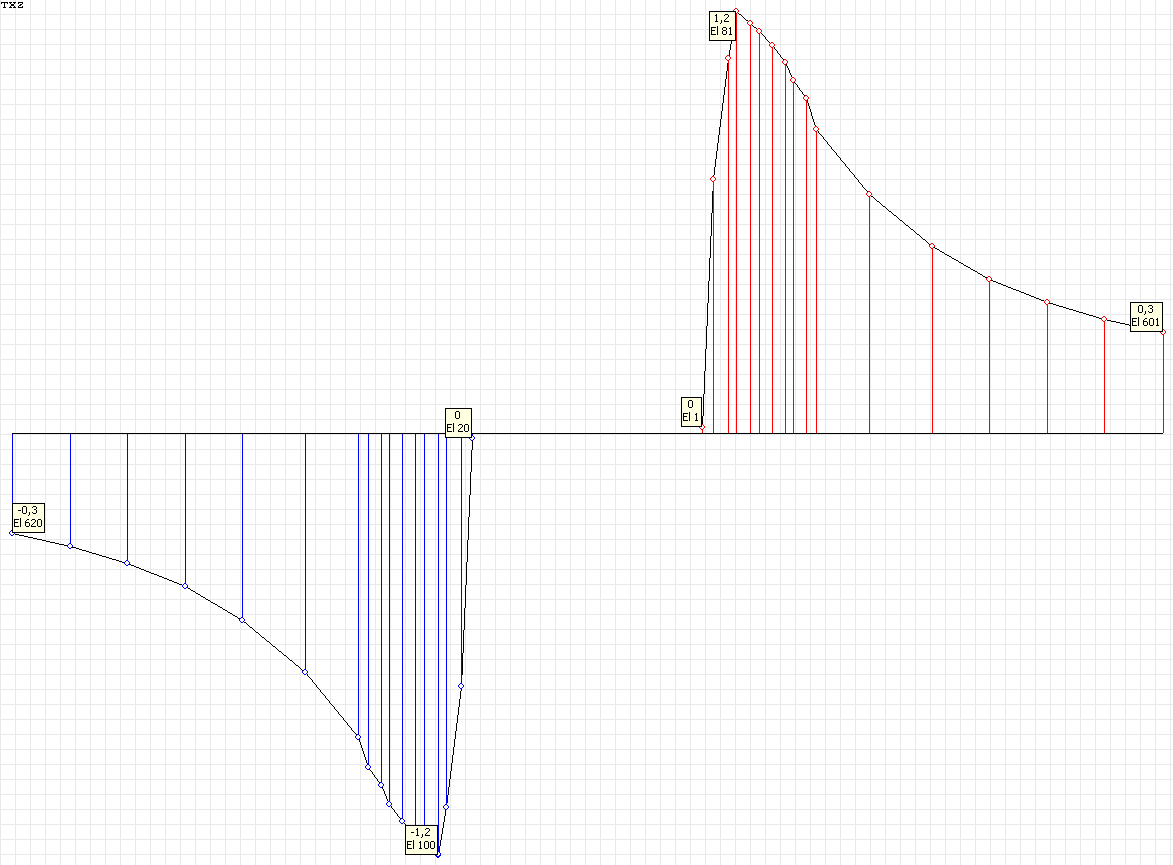
Эпюра напряжений σ_rθ (кН/м²) при угле наклона к оси Ox₁ θ = 0º для расчетной схемы по варианту 1

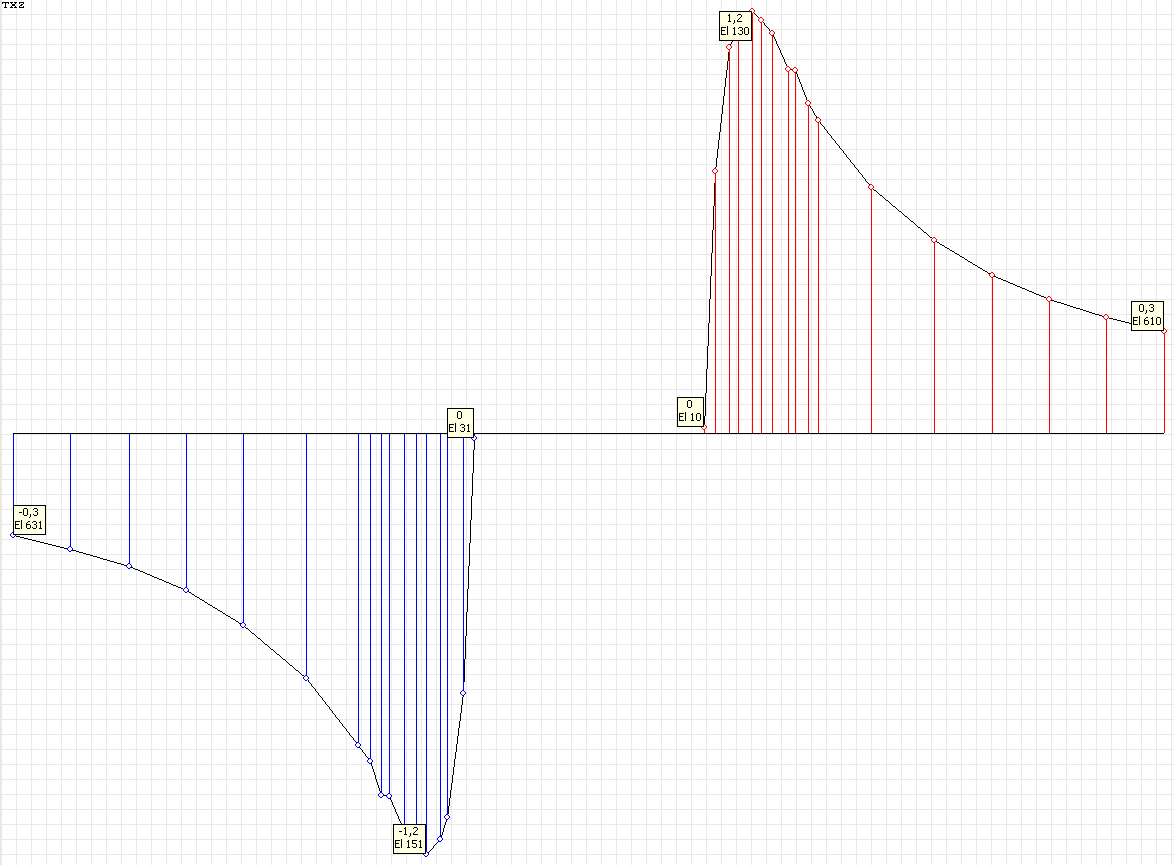
Эпюра напряжений σ_rθ (кН/м²) при угле наклона к оси Ox₁ θ = 90º для расчетной схемы по варианту 1

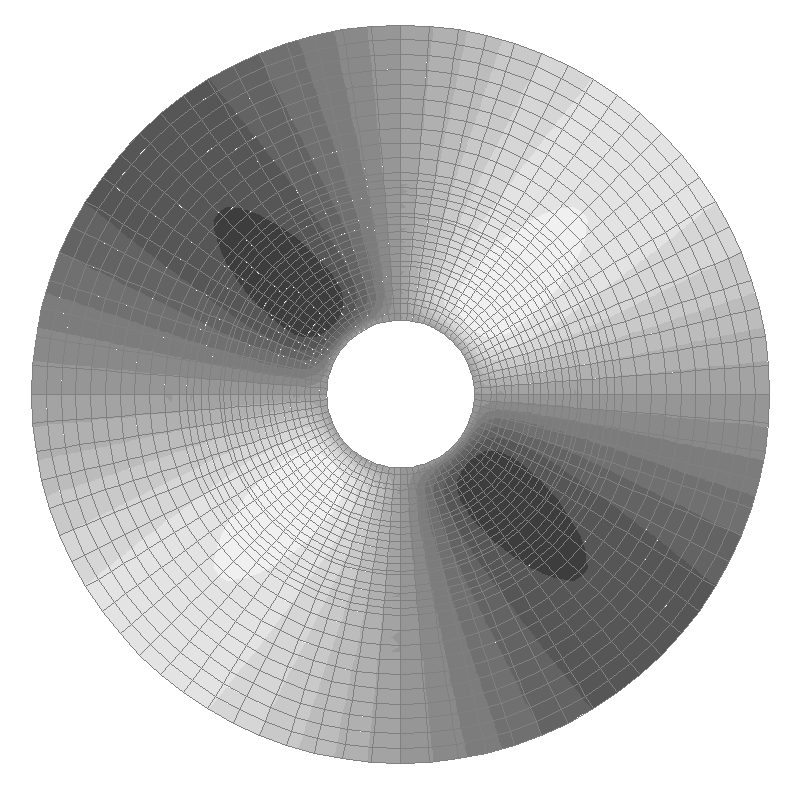
Значения напряжений σ_rθ (кН/м²) для расчетной схемы по варианту 2

Эпюра напряжений σ_rθ (кН/м²) при угле наклона к оси Ox₁ θ = 0º для расчетной схемы по варианту 2

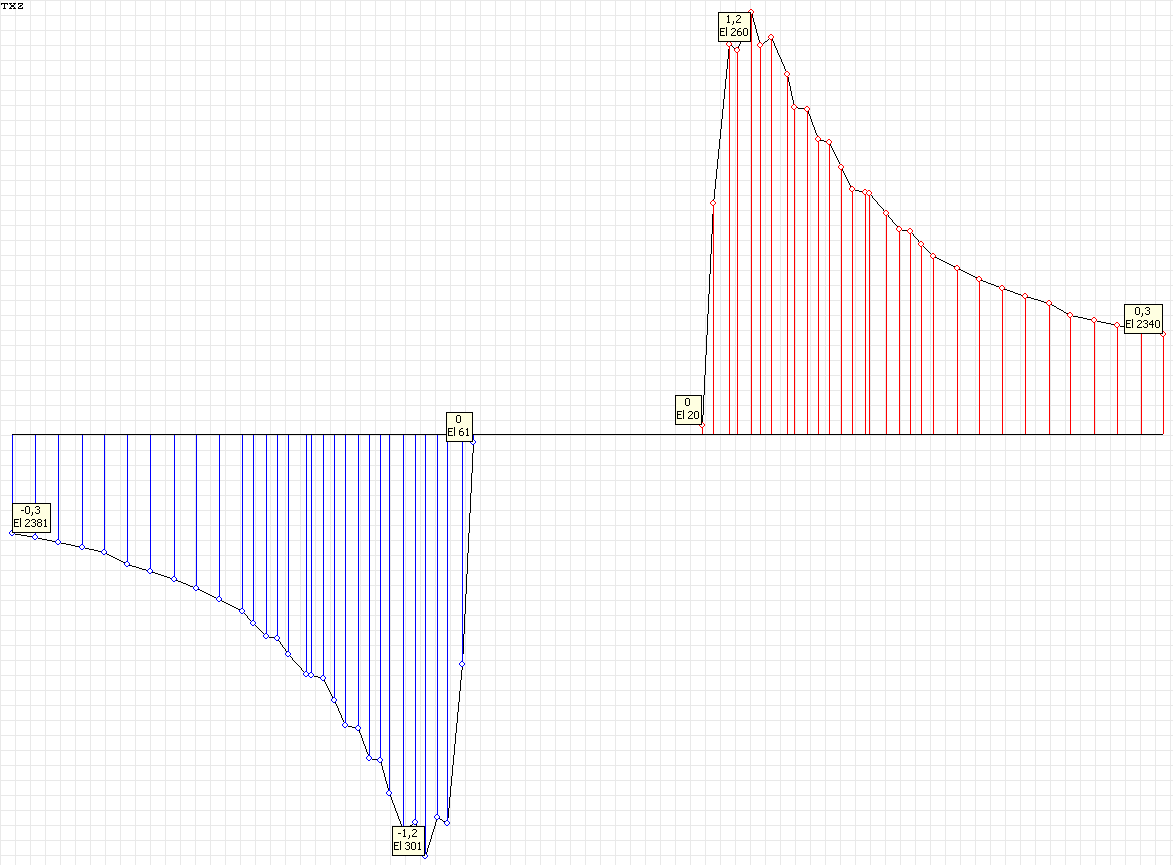
Эпюра напряжений σ_rθ (кН/м²) при угле наклона к оси Ox₁ θ = 90º для расчетной схемы по варианту 2

Сравнение решений:

Компоненты тензора напряжений в полярных координатах σ_rr, σ_θθ, σ_rθ.

Реше­ние	Напряжения σrr (кН/м2)					Напряжения σθθ (кН/м2)
	θ = 0º			θ = 90º		θ = 0º			θ = 90º
	r  = 1.000 м	r  =  (√6/5)·a = 1.095 м	r  =  (√3/2)·a = 1.225 м	r  = 1.000 м	r  = (√2)·a = 1.414 м	r  = 1.000 м	r  = (√3)·a = 1.732 м	r  = (√6)·a = 2.449 м	r  = 1.000 м
Тео­рия	0.00	-σ/24 = -4.17	0.00	0.00	3·σ/8 = 37.50	-σ = -100.00	0.00	σ/24 = 4.17	3·σ = 300.00
SCAD, РС вар.1	-1.32	-5.65	-1.26	2.77	39.43	-100.63	-1.18	3.56	307.46
Отклонения, %	-	-	-	-	5.15	0.63	-	-	2.49
SCAD, РС вар.2	-0.76	-4.78	-0.36	1.31	37.94	-100.05	-0.04	4.16	299.85
Отклонения, %	-	-	-	-	1.17	0.05	-	-	0.05

Замечания: При аналитическом решении напряжения σ_rr, σ_θθ, σ_rθ  в пластине с малым круговым отверстием от воздействия одностороннего равномерного растяжения определяются по следующим формулам (С.П. Демидов, Теория упругости. — Москва: Высшая школа, 1979, стр. 302):

\[ \sigma_{rr} =\frac{\sigma }{2}\cdot \left( {1-\frac{a^{2}}{r^{2}}} \right)+\frac{\sigma }{2}\cdot \left( {1-4\cdot \frac{a^{2}}{r^{2}}+3\cdot \frac{a^{4}}{r^{4}}} \right)\cdot \cos \left( {2\cdot \theta } \right); \] \[ \sigma_{\theta \theta } =\frac{\sigma }{2}\cdot \left( {1+\frac{a^{2}}{r^{2}}} \right)-\frac{\sigma }{2}\cdot \left( {1+3\cdot \frac{a^{4}}{r^{4}}} \right)\cdot \cos \left( {2\cdot \theta } \right); \] \[ \sigma_{r\theta } =-\frac{\sigma }{2}\cdot \left( {1+2\cdot \frac{a^{2}}{r^{2}}-3\cdot \frac{a^{4}}{r^{4}}} \right)\cdot \sin \left( {2\cdot \theta } \right). \]