Напряженно-деформированное состояние кольцевой шарнирно опертой пластины, нагруженной поперечной равномерно распределенной нагрузкой
Цель: Определение напряженно-деформированного состояния кольцевой шарнирно опертой пластины постоянной толщины, нагруженной поперечной равномерно распределенной нагрузкой.
Файл с исходными данными: 4_16.spr
Формулировка задачи: Кольцевая шарнирно опертая пластина постоянной толщины нагружается поперечной равномерно распределенной нагрузкой. Определить прогиб w, радиальный Mr и тангенциальный Mθ изгибающие моменты по внутреннему и по наружному контуру пластины.
Ссылки: С.П. Тимошенко, Пластинки и оболочки. — Москва: ОГИЗ, Гостехиздат, 1948.
Исходные данные:
| E = 2.0·108 кПа | - модуль упругости; |
| μ = 0.3 | - коэффициент Пуассона; |
| R = 1.2 м | - наружный радиус пластины; |
| r = 0.6 м | - внутренний радиус пластины; |
| h = 2.0·10-2 м | - толщина пластины; |
| p = 10 кПа | - поперечная равномерно распределенная нагрузка. |
Конечноэлементная модель: Расчетная схема – система общего вида, элементы пластины – 288 восьмиузловых элементов типа 50. Направление выдачи внутренних усилий – радиально-тангенциальное. Обеспечение граничных условий достигается за счет наложения связей по направлению степени свободы Z по наружному контуру пластины. Количество узлов в расчетной схеме – 960.
Результаты решения в SCAD
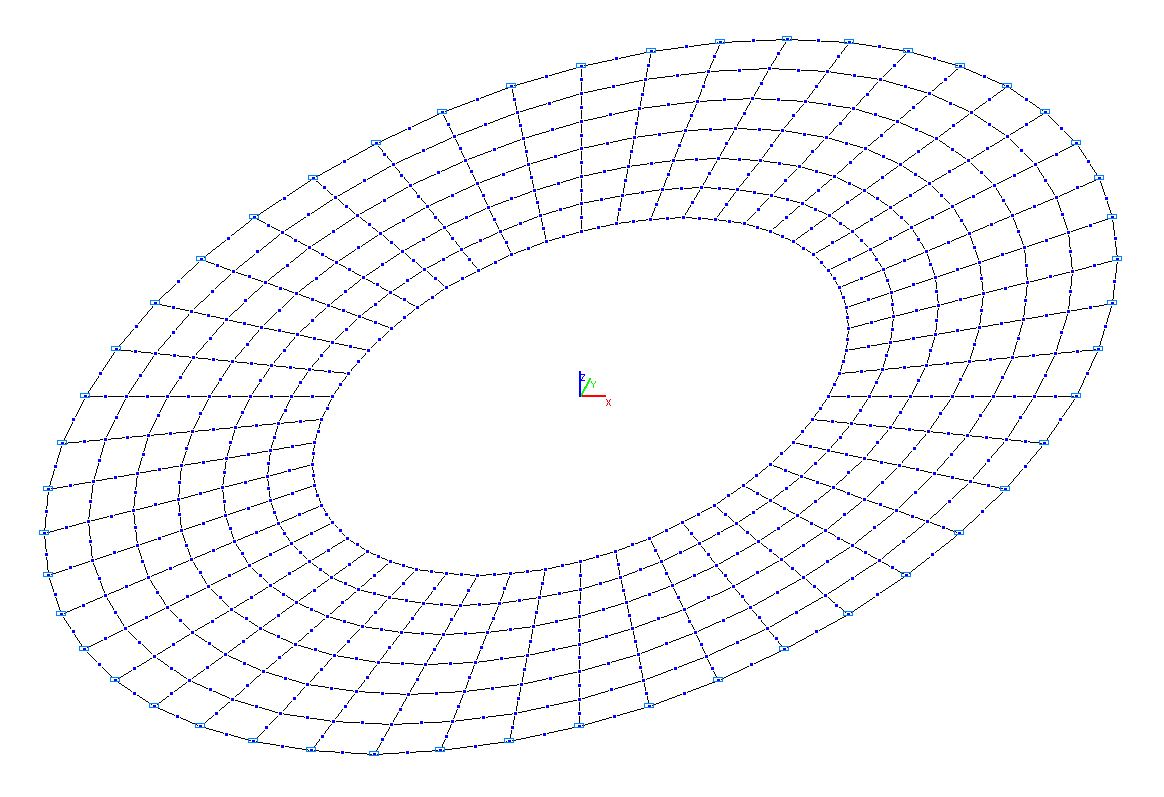
Расчетная схема
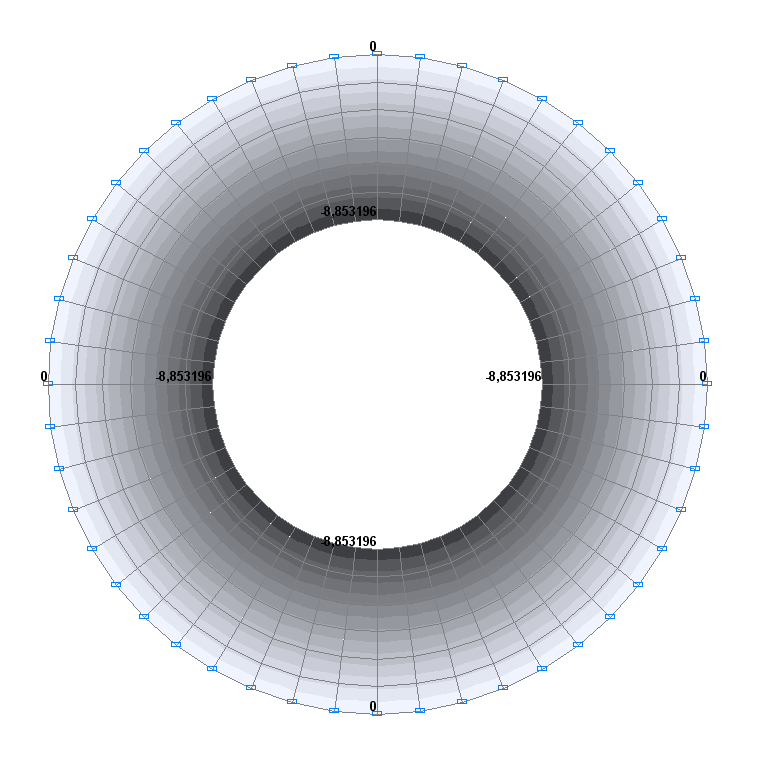

Значения прогибов w (мм)
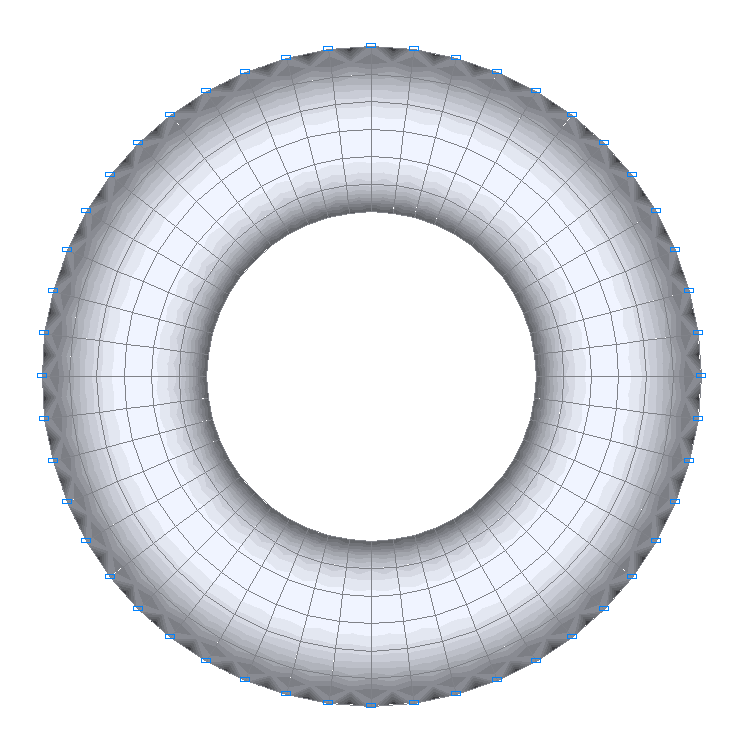

Значения радиальных изгибающих моментов Mr (кН·м/м)
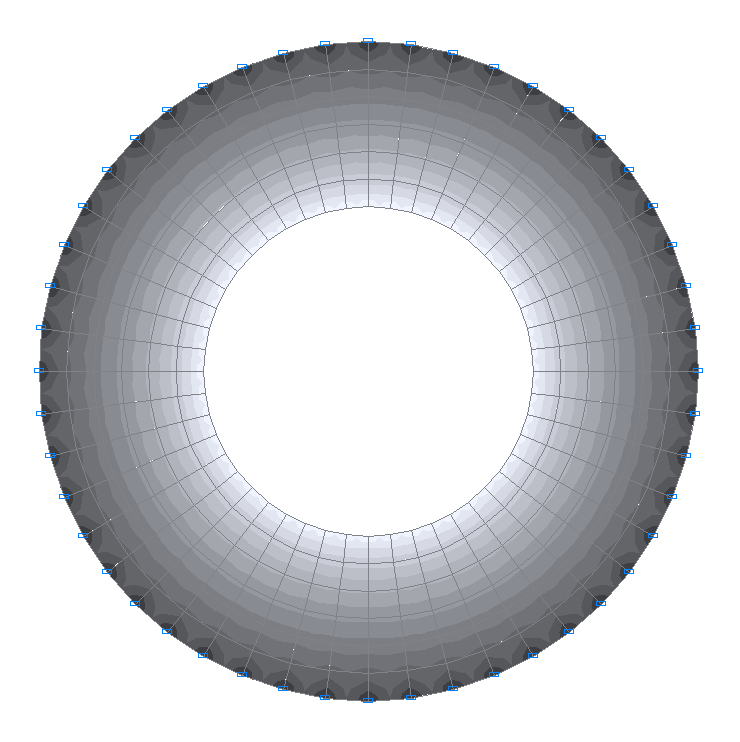
Значения тангенциальных изгибающих моментов Mθ (кН·м/м)
Сравнение решений:
|
Параметр |
По внутреннему контуру пластины |
По наружному контуру пластины |
||||
|---|---|---|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
Теория |
SCAD |
Отклонения, % |
|
|
w, мм |
-8.933 |
-8.863 |
0.78 |
0.000 |
0.000 |
- |
|
Mr, кН·м/м |
0.000 |
0.001 |
- |
0.000 |
0.052 |
- |
|
Mθ, кН·м/м |
3.462 |
3.474 |
0.35 |
1.574 |
1.547 |
1.72 |
Замечания: При аналитическом решении прогиб w, радиальный Mr и тангенциальный Mθ изгибающие моменты по внутреннему контуру пластины могут быть вычислены по следующим формулам (С.П. Тимошенко. Пластинки и оболочки. — Москва: ОГИЗ, Гостехиздат, 1948. стр. 71):
\[w=-\frac{q}{64\cdot D}\cdot \left[ {\frac{R^{2}-r^{2}}{1+\mu }\cdot \left( {R^{2}\cdot \left( {5+\mu } \right)-r^{2}\cdot \left( {7+2\cdot \mu } \right)} \right)-\frac{4\cdot R^{2}\cdot r^{2}}{1-\mu }\cdot \ln \frac{r}{R}\cdot \left( {3+\mu +\frac{4\cdot r^{2}}{R^{2}-r^{2}}\cdot \left( {1+\mu } \right)\cdot \ln \frac{r}{R}} \right)} \right], где: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}; \] \[ M_{r} =0; \] \[ M_{\theta } =\frac{q}{8}\cdot \left[ {R^{2}\cdot \left( {3+\mu } \right)-r^{2}\cdot \left( {1-\mu } \right)+\frac{4\cdot R^{2}\cdot r^{2}}{R^{2}-r^{2}}\cdot \ln \frac{r}{R}\cdot \left( {1+\mu } \right)} \right]. \]
При аналитическом решении прогиб w, радиальный Mr и тангенциальный Mθ изгибающие моменты по наружному контуру пластины могут быть вычислены по следующим формулам (С.П. Тимошенко. Пластинки и оболочки. — Москва: ОГИЗ, Гостехиздат, 1948. стр. 71):
\[ w=0; \] \[ M_{r} =0; \] \[ M_{\theta } =\frac{q}{8}\cdot \left[ {R^{2}\cdot \left( {1-\mu } \right)+r^{2}\cdot \left( {1+3\cdot \mu } \right)+\frac{4\cdot R^{4}}{R^{2}-r^{2}}\cdot \ln \frac{r}{R}\cdot \left( {1+\mu } \right)} \right]. \]
