Прямоугольная свободно опертая по периметру пластина под действием поперечной равномерно распределенной нагрузки
Цель: Определение напряженно-деформированного состояния прямоугольной свободно опертой по периметру пластины от воздействия поперечной равномерно распределенной нагрузки.
Файлы с исходными данными:
| SSLS24_b_1a_v11.3.spr | Расчетная схема с соотношениями сторон пластины b/a = 1.0 |
| SSLS24_b_2a_v11.3.spr | Расчетная схема с соотношениями сторон пластины b/a = 2.0 |
| SSLS24_b_5a_v11.3.spr | Расчетная схема с соотношениями сторон пластины b/a = 5.0 |
Формулировка задачи: Прямоугольная свободно опертая по периметру пластина находится под воздействием поперечной равномерно распределенной по ее площади нагрузки p. Определить поперечное перемещение Z и изгибающие моменты Mx, My в центре пластины при различных соотношениях размеров ее сторон b/a.
Ссылки: S. Timoshenko, S. Woinowski, Theorie des plaques et des coques, Paris, Librairie Polytechnique Beranger, 1961.
Исходные данные:
| E = 1.0·107 Па | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| h = 0.01 м | - толщина пластины; |
| a = 1.0 м | - размер короткой стороны пластины (вдоль оси X общей системы координат); |
| b = 1.0 м, 2.0 м, 5.0 м | - размер длинной стороны пластины (вдоль оси Y общей системы координат); |
| p = 1.0 Н/м2 | - значение поперечной равномерно распределенной нагрузки. |
Конечноэлементная модель: Рассматриваются три расчетные схемы.
Расчетная схема 1 (b/a = 1.0) – балочный ростверк / плита, элементы оболочки – 100 элементов плиты типа 20. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы Z, UY для кромок, расположенных вдоль оси X общей системы координат, и Z, UX для кромок, расположенных вдоль оси Y общей системы координат. Количество узлов в расчетной схеме – 121.
Расчетная схема 2 (b/a = 2.0) – балочный ростверк / плита, элементы оболочки – 200 элементов плиты типа 20. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы Z, UY для кромок, расположенных вдоль оси X общей системы координат, и Z, UX для кромок, расположенных вдоль оси Y общей системы координат. Количество узлов в расчетной схеме – 231.
Расчетная схема 3 (b/a = 5.0) – балочный ростверк / плита, элементы оболочки – 500 элементов плиты типа 20. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы Z, UY для кромок, расположенных вдоль оси X общей системы координат, и Z, UX для кромок, расположенных вдоль оси Y общей системы координат. Количество узлов в расчетной схеме – 561.
Результаты решения в SCAD
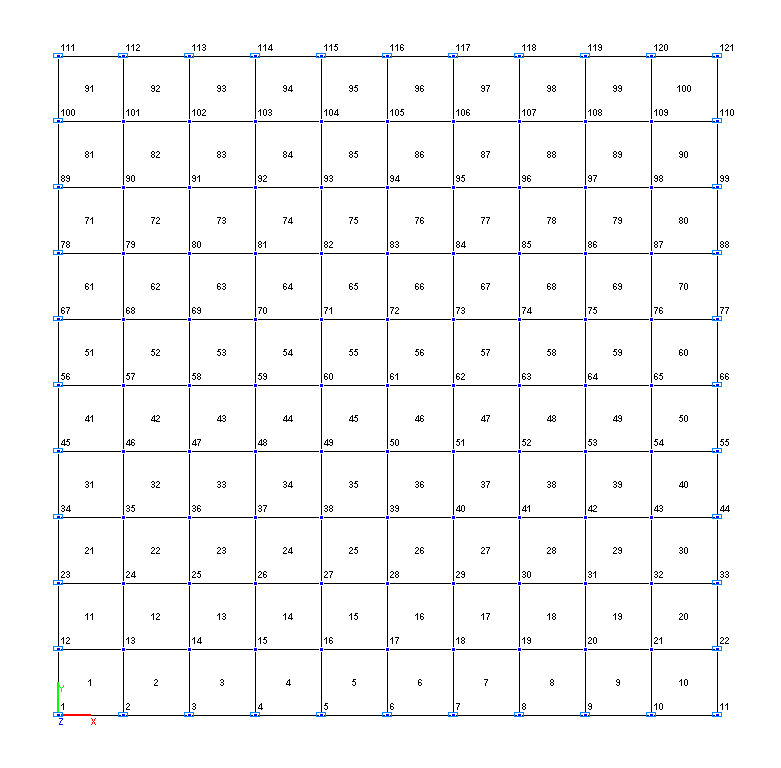

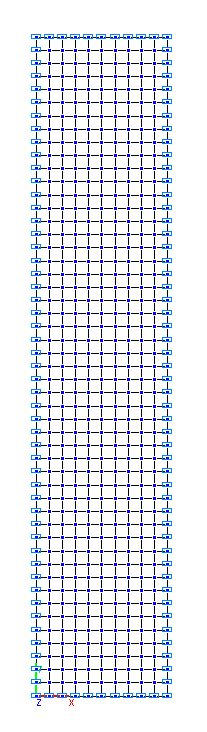
Расчетные схемы 1, 2, 3
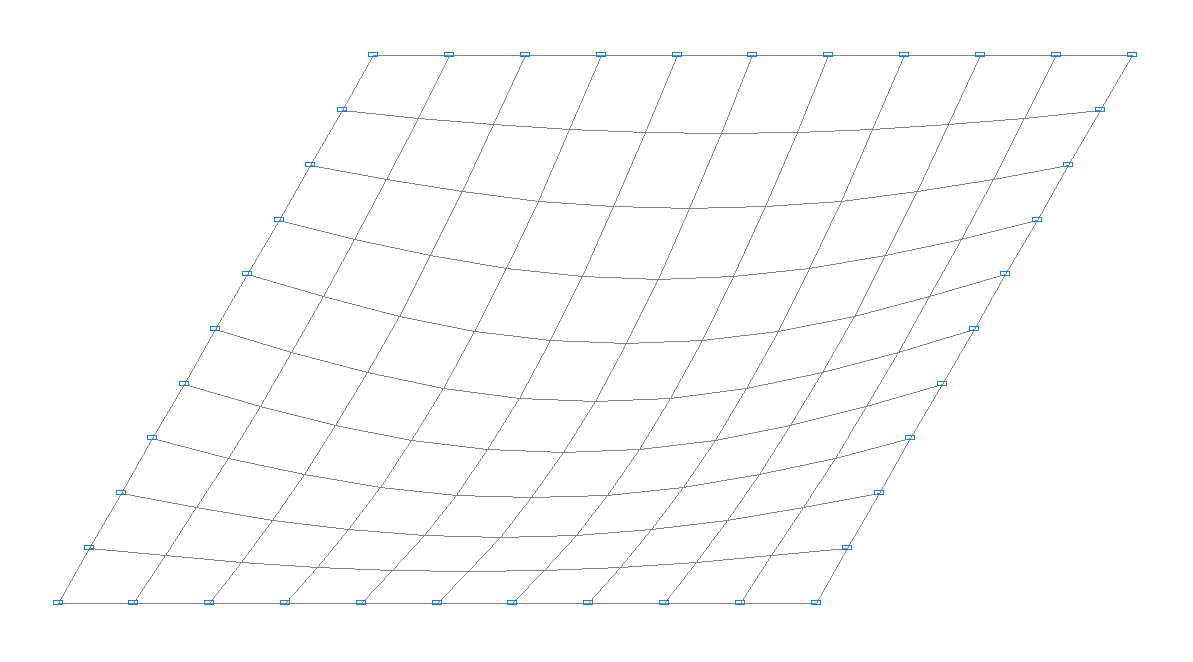
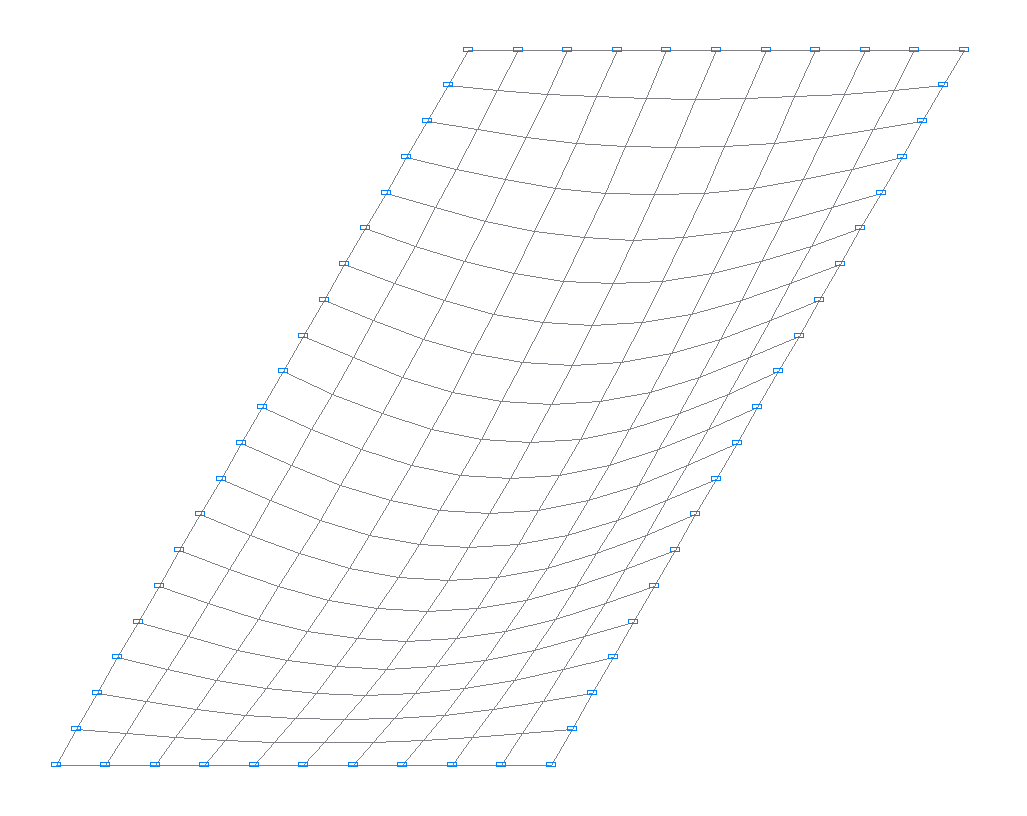

Деформированные схемы 1, 2, 3
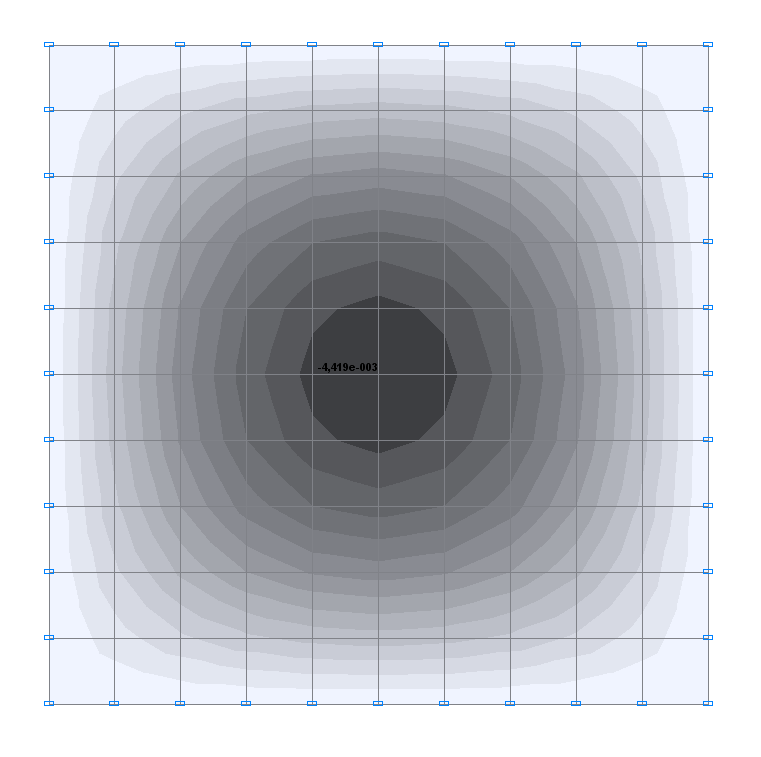
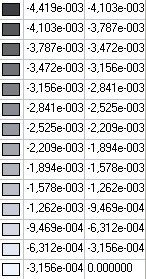
Значения поперечных перемещений Z (м) для расчетной схемы 1
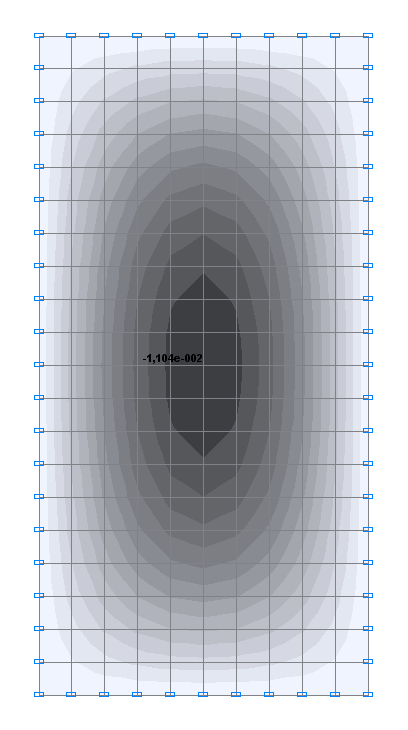
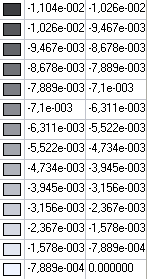
Значения поперечных перемещений Z (м) для расчетной схемы 2

Значения поперечных перемещений Z (м) для расчетной схемы 3
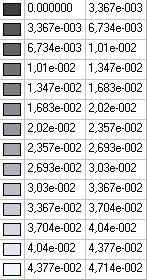
Значения изгибающих моментов Mx (Н·м/м) для расчетной схемы 1
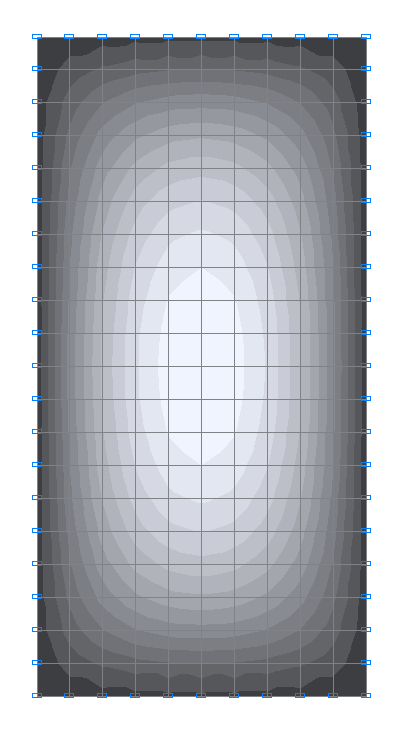
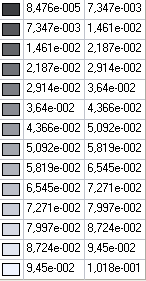
Значения изгибающих моментов Mx (Н·м/м) для расчетной схемы 2
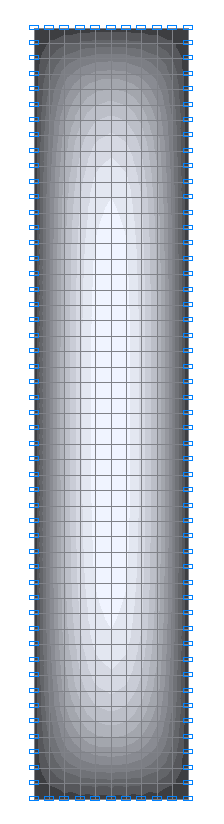
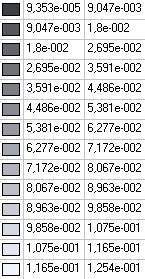
Значения изгибающих моментов Mx (Н·м/м) для расчетной схемы 3

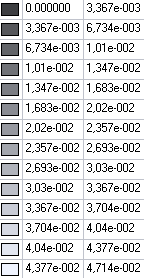
Значения изгибающих моментов My (Н·м/м) для расчетной схемы 1
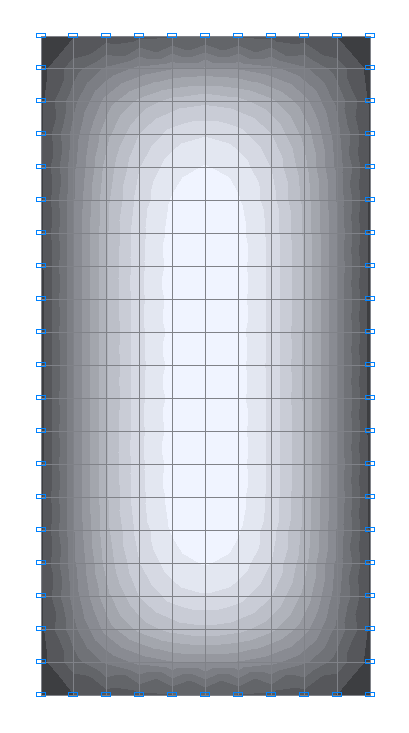
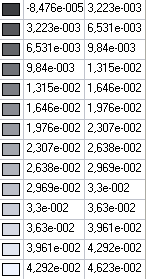
Значения изгибающих моментов My (Н·м/м) для расчетной схемы 2
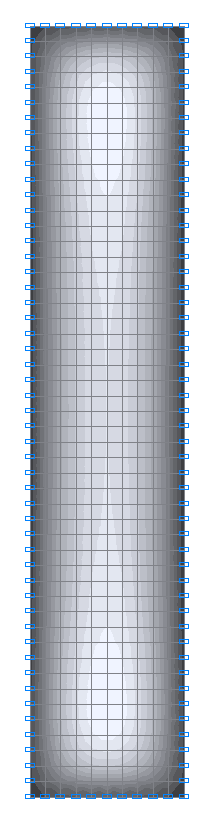
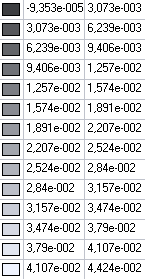
Значения изгибающих моментов My (Н·м/м) для расчетной схемы 3
Сравнение решений:
Расчетная схема 1 (b/a = 1.0)
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Поперечное перемещение Z в центре пластины, м |
-4.436∙10-3 |
-4.419∙10-3 |
0.38 |
|
Изгибающие моменты Mx в центре пластины, Н·м/м |
4.789∙10-2 |
4.714∙10-2 |
1.57 |
|
Изгибающие моменты My в центре пластины, Н·м/м |
4.789∙10-2 |
4.714∙10-2 |
1.57 |
Расчетная схема 2 (b/a = 2.0)
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Поперечное перемещение Z в центре пластины, м |
-1.106∙10-2 |
-1.104∙10-2 |
0.18 |
|
Изгибающие моменты Mx в центре пластины, Н·м/м |
1.017∙10-2 |
1.018∙10-2 |
0.10 |
|
Изгибающие моменты My в центре пластины, Н·м/м |
4.635∙10-2 |
4.607∙10-2 |
0.60 |
Расчетная схема 3 (b/a = 5.0)
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Поперечное перемещение Z в центре пластины, м |
-1.416∙10-2 |
-1.416∙10-2 |
0.00 |
|
Изгибающие моменты Mx в центре пластины, Н·м/м |
1.246∙10-1 |
1.254∙10-1 |
0.64 |
|
Изгибающие моменты My в центре пластины, Н·м/м |
3.774∙10-2 |
3.798∙10-2 |
0.64 |
Замечания: При аналитическом решении поперечное перемещение Z и изгибающие моменты Mx, My в центре пластины при различных соотношениях размеров ее сторон b/a могут быть вычислены по следующим формулам:
\[ Z=\alpha \cdot \frac{p\cdot a^{4}}{D}; \quad M_{x} =\beta \cdot p\cdot a^{2}; \quad M_{y} =\beta_{1} \cdot p\cdot a^{2}, \quad где: \] \[ при \quad \frac{a}{b}=1.0 \quad \alpha =0.004062, \quad \beta =0.047886, \quad \beta_{1}=0.047886, \] \[ при \quad \frac{a}{b}=2.0 \quad \alpha =0.010129, \quad \beta =0.101683, \quad \beta_{1}=0.046350, \] \[ при \quad \frac{a}{b}=5.0 \quad \alpha =0.012971, \quad \beta =0.124624, \quad \beta_{1}=0.037744,\] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}. \]
