Напряженно-деформированное состояние защемленной шестиугольной пластины под равномерно распределенной нагрузкой
Цель: Определение перемещений и изгибающих моментов в центре защемленной по периметру шестиугольной пластины под равномерно распределенной нагрузкой q.
Файл с исходными данными: 4_19.spr
Формулировка задачи: Шестиугольная правильная пластина, защемленная по контуру, постоянной толщины нагружается нормальным давлением q. Определить: осевое перемещение w и изгибающие моменты Mx, My в центре пластины.
Ссылки: Вайнберг Д.В, Справочник по прочности, устойчивости и колебаниям пластин. Киев: Будiвельник, 1973.
Исходные данные:
| E = 2.0·108 кПа | - модуль упругости, |
| μ = 0.3 | - коэффициент Пуассона, |
| a = 0.134 м | - сторона шестигранной пластины, |
| h = 0.003 м | - толщина пластины, |
| q = 1000 кПа | - нормальное давление, |
Связи: жесткое закрепление узлов по контуру (перемещение w = 0)
Конечноэлементная модель: Расчетная схема – система общего вида. Элементы пластины – 389 четырехузловых элементов типа 44 и 73 трехузловых элемента типа 42. Количество узлов в расчетной схеме – 451.
Результаты решения в SCAD

Расчетная схема
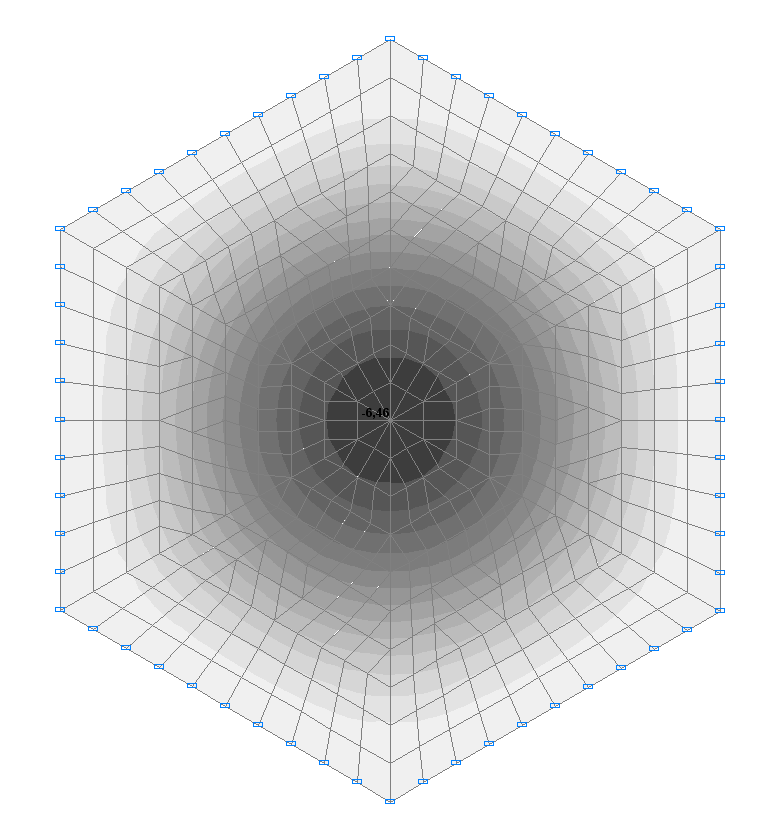

Значения перемещений w (мм)


Значения изгибающих моментов Mx (кН·м/м)


Значения изгибающих моментов My (кН·м/м)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Перемещение в центре пластины w, мм |
6.51 |
6.46 |
0.77 |
|
Изгибающий момент Мх, кН∙м /м |
1.163 |
1.171 |
0.69 |
|
Изгибающий момент Му, кН∙м /м |
1.163 |
1.171 |
0.69 |
Замечания: При аналитическом решении формулы для перемещений w и изгибающих моментов Mx и My в центре пластины имеют следующий вид (Вайнберг Д.В., Справочник по прочности, устойчивости и колебаниям пластин, Киев: Будiвельник, 1973):
\[w=0.009979\cdot \frac{q\cdot a^{4}}{D}, где: \]\[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}; \] \[ M_{x} =M_{y} =0.049835\cdot \left( {1+\mu } \right)\cdot q\cdot a^{2}. \]
