Прямоугольная защемленная по контуру пластина постоянной толщины при температурном нагружении
Цель: Определить изгибающие моменты и напряжения в прямоугольной пластине, защемленной по контуру при изменении температуры по толщине пластины по линейному закону.
Файл с исходными данными: 4_20.spr
Формулировка задачи: Рассматривается защемленная по контуру прямоугольная пластина постоянной толщины. Температура в плоскостях, параллельных срединной поверхности пластины постоянна, а по толщине пластины изменяется по линейному закону. Определить: перемещение w, изгибающие моменты Mx, My и максимальное температурное напряжение σ.
Ссылки: С.П. Тимошенко, С.Войновский-Кригер, Пластинки и оболочки. — М.: Наука, 1963.
Исходные данные:
| E = 2.0·108 кПа | - модуль упругости, |
| μ = 0.3 | - коэффициент Пуассона, |
| aх = 1.5 м | - ширина пластины, |
| aу = 2.5 м | - длина пластины |
| h = 0.02 м | - толщина пластины, |
| α= 1.5·10-5 1/С0 | - коэффициент линейного температурного расширения материала, |
| ΔТ = 20 С0 | - разность температур между верхней и нижней поверхностями пластины |
Связи: жесткое закрепление узлов по контуру (перемещение u=v=w = θx = θy= θz = 0)
Конечноэлементная модель: Расчетная схема – система общего вида. Элементы пластины – 200 четырехузловых элементов типа 41. Количество узлов в расчетной схеме – 231.
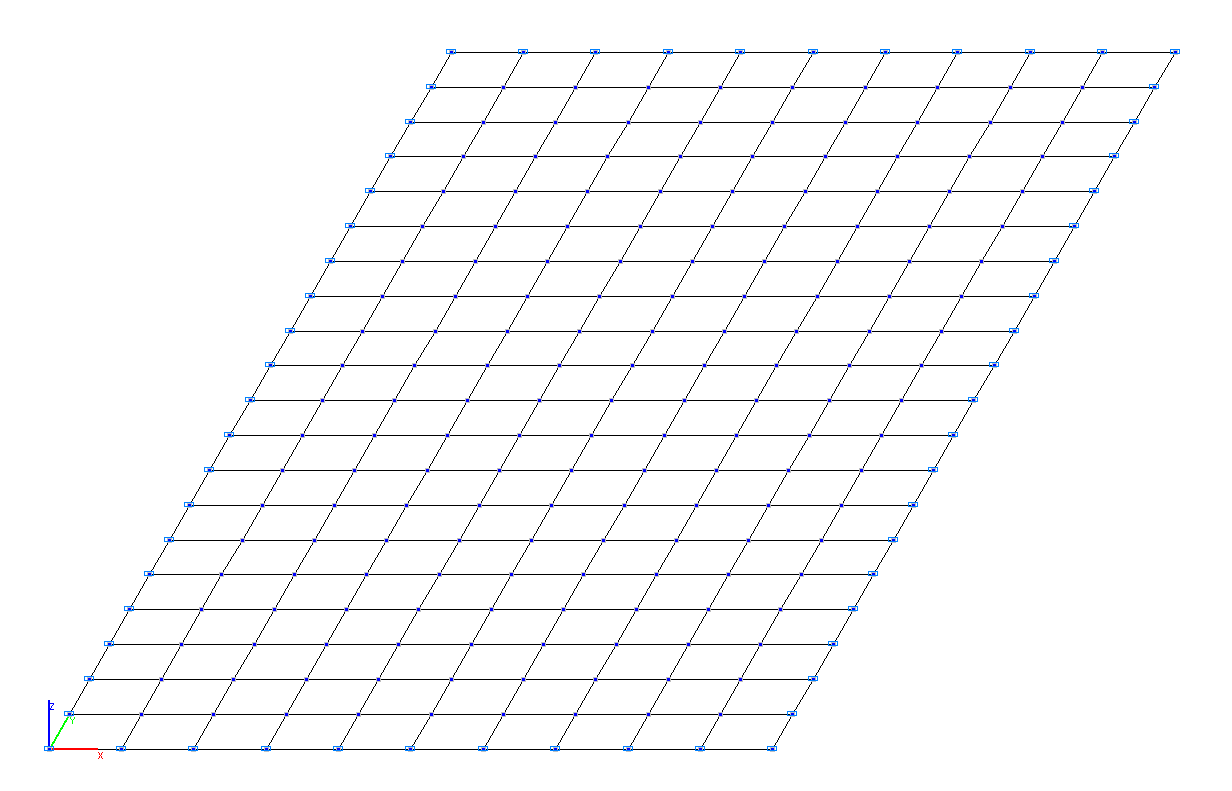
Расчетная схема
Результаты решения в SCAD
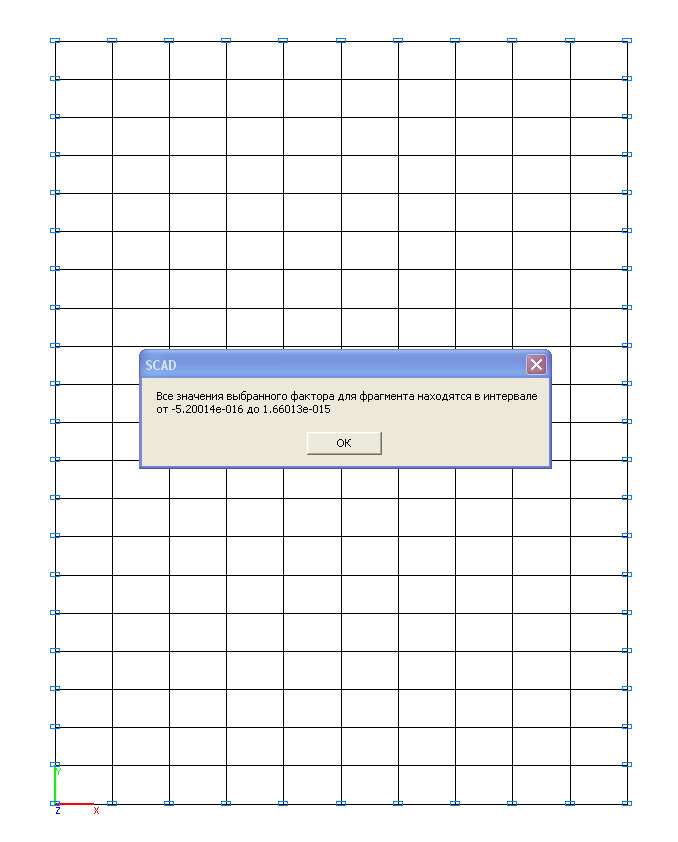
Значения перемещений w (мм)
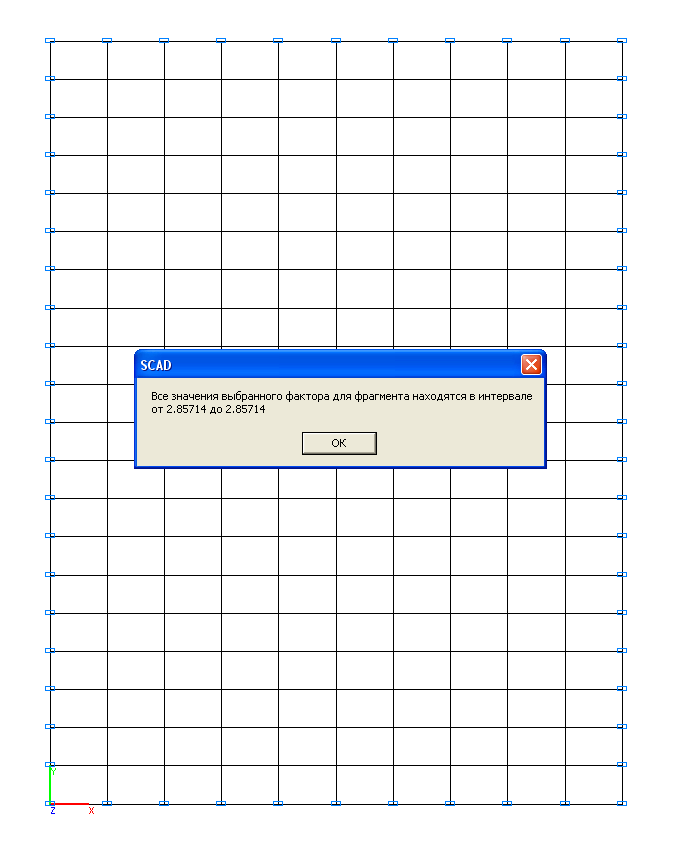
Значения изгибающих моментов Mx (кН·м/м)
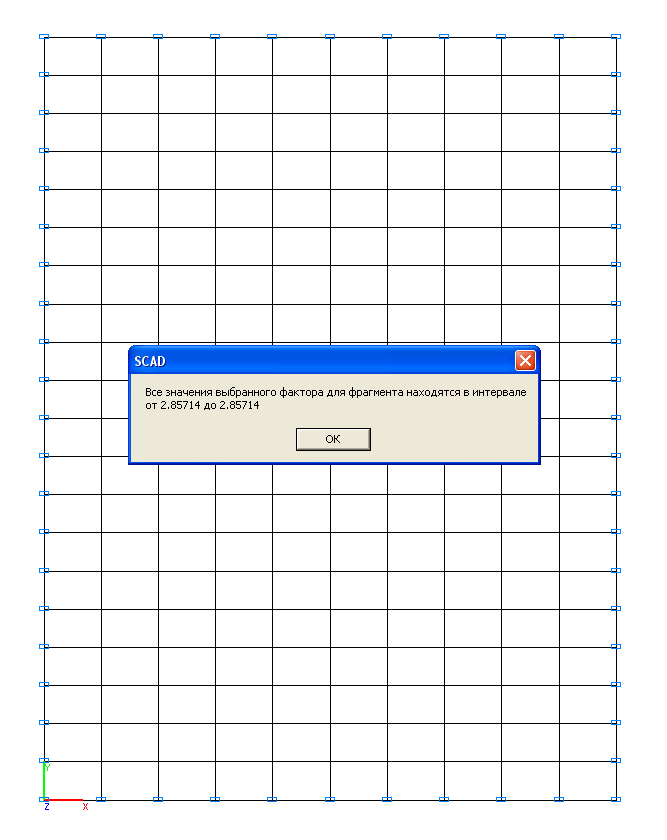
Значения изгибающих моментов My (кН·м/м)
Значения напряжений на верхней поверхности пластины σ (кН/м2)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Перемещение w, мм |
0.00 |
0.00 |
- |
|
Изгибающие моменты Мх = Му , кН∙м /м |
2.857 |
2.857 |
0.00 |
|
Наибольшие температурные напряжения, кПа |
42857 |
42857 |
0.00 |
Замечания: При аналитическом решении формулы для изгибающих моментов Mx, My и максимальных температурных напряжений σ в заделанной пластине при изменении температуры по толщине пластины по линейному закону имеют следующий вид (С.П. Тимошенко, С.Войновский-Кригер, Пластинки и оболочки. — М.: Наука, 1963, стр. 64):
\[M_{x} =M_{y} =D\cdot \frac{\alpha \cdot \Delta T\cdot \left( {1+\mu } \right)}{h}, где: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}, \] \[ \sigma =\frac{\alpha \cdot \Delta T\cdot E}{2\cdot \left( {1-\mu } \right)}. \]