Толстая квадратная шарнирно-опертая пластина под действием поперечной равномерно распределенной нагрузки

Цель: Определение деформированного состояния толстой квадратной шарнирно-опертой пластины от воздействия поперечной равномерно распределенной нагрузки.

Файлы с исходными данными:

толстая_плита_a_h_2.spr	Расчетная модель для отношений размеров стороны плиты к толщине a/h = 2.0
толстая_плита_a_h_4.spr	Расчетная модель для отношений размеров стороны плиты к толщине a/h = 4.0
толстая_плита_a_h_8.spr	Расчетная модель для отношений размеров стороны плиты к толщине a/h = 8.0

 

Формулировка задачи: Толстая квадратная шарнирно-опертая пластина находится под воздействием поперечной равномерно распределенной нагрузки p. Определить прогиб w в центре пластины с учетом деформаций поперечного сдвига.

Ссылки: Л. Г. Доннелл, Балки, пластины и оболочки, Москва, Наука, 1982, стр. 313-316.

Исходные данные:

E = 3.0·107 кПа	- модуль упругости,
ν = 0.2	- коэффициент Пуассона,
h = 2.0; 4.0; 8.0 м	- толщина пластины;
a = 16.0 м	- размер стороны пластины;
p = 100.0 кН/м2	- значение поперечной равномерно распределенной нагрузки.

 

Конечноэлементная модель: Рассматриваются три расчетные модели для отношений размеров стороны плиты к толщине a/h = 8.0; 4.0; 2.0. В каждой модели рассматриваются четыре расчетные схемы с типами конечных элементов: 44, 50 – четырехугольные четырехузловой и восьмиузловой элементы тонких оболочек для расчета по теории Кирхгофа-Лява; 144, 150 – четырехугольные четырехузловой и восьмиузловой элементы толстых оболочек для расчета по теории Рейсснера-Миндлина.

Расчетные схемы строятся для сеток с размерностями: 2x2; 4x4; 8x8; 16x16; 32x32; 64x64.

Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы X, Y, Z, UY для кромок, расположенных вдоль оси X общей системы координат, и X, Y, Z, UX для кромок, расположенных вдоль оси Y общей системы координат.

Результаты решения в SCAD

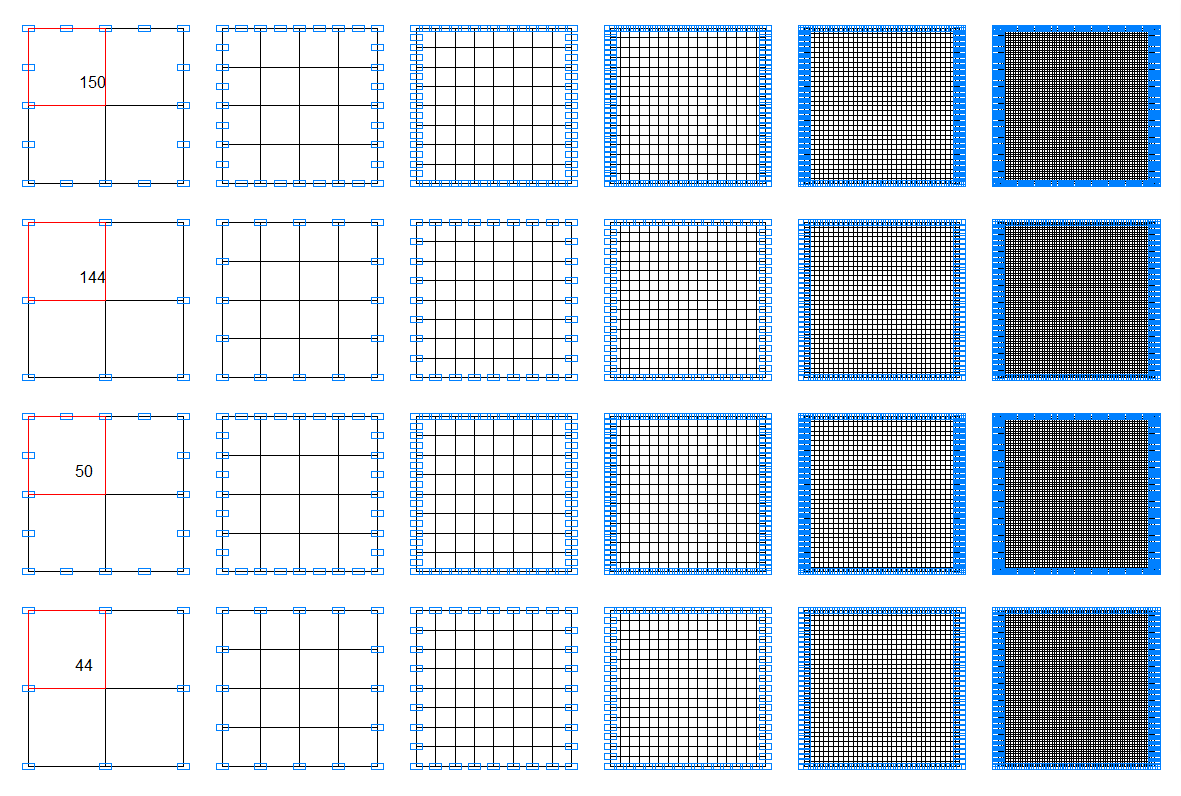
Расчетные схемы

Прогибы w пластин с отношением a/h = 8.0, м

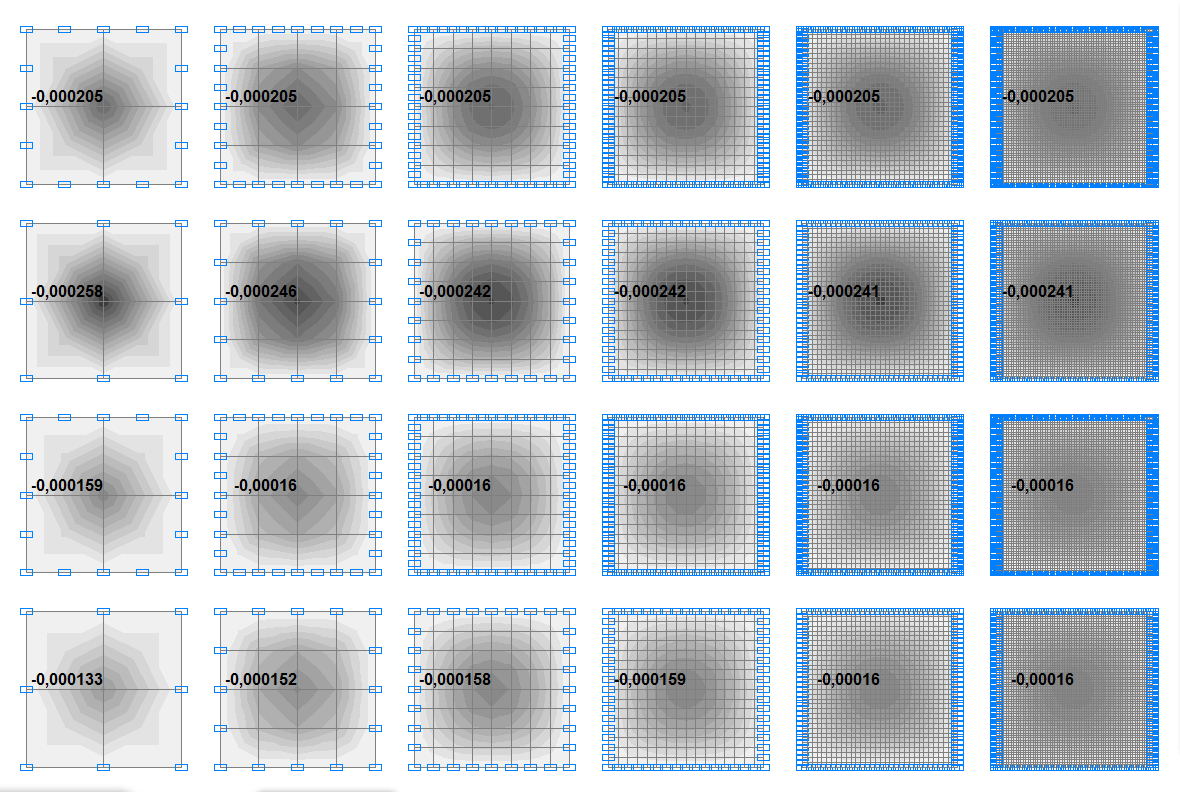
Прогибы w пластин с отношением a/h = 4.0, м

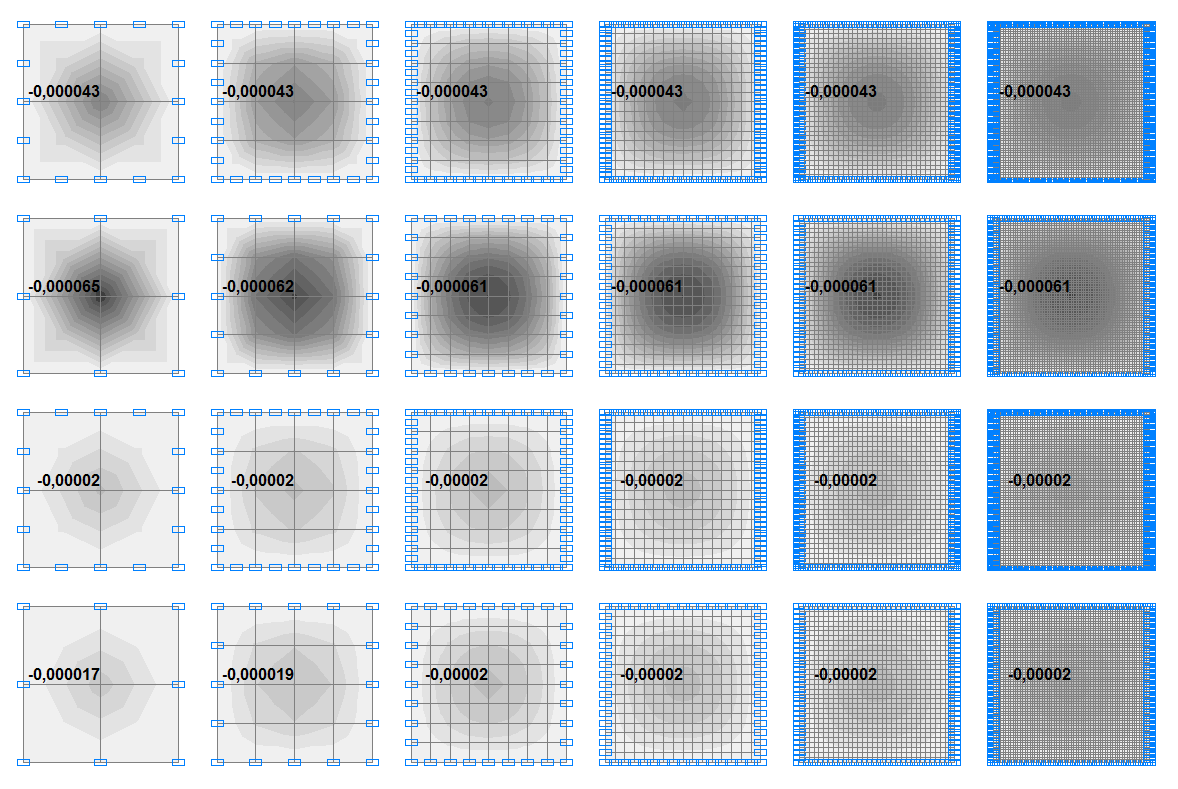
Прогибы w пластин с отношением a/h = 2.0, м

Сравнение решений:

Прогибы w в центре пластин с отношением a/h = 8.0, м

Тип элемента	SCAD, сетка						Теория	Отклонение
	2x2	4x4	8x8	16x16	32x32	64x64
44	0.001065	0.001213	0.001262	0.001274	0.001277	0.001278	0.001278	0.00 %
50	0.001276	0.001278	0.001278	0.001278	0.001278	0.001278		0.00 %
144	0.001472	0.001472	0.001449	0.001443	0.001441	0.001441	0.001369	5.26 %
150	0.001314	0.001364	0.001368	0.001368	0.001368	0.001368		0.07 %

Прогибы w в центре пластин с отношением a/h = 4.0, м

Тип элемента	SCAD, сетка						Теория	Отклонение
	2x2	4x4	8x8	16x16	32x32	64x64
44	0.000133	0.000152	0.000158	0.000159	0.000160	0.000160	0.000160	0.00 %
50	0.000159	0.000160	0.000160	0.000160	0.000160	0.000160		0.00 %
144	0.000258	0.000246	0.000242	0.000242	0.000241	0.000241	0.000205	17.56 %
150	0.000205	0.000205	0.000205	0.000205	0.000205	0.000205		0.00 %

Прогибы w в центре пластин с отношением a/h = 2.0, м

Тип элемента	SCAD, сетка						Теория	Отклонение
	2x2	4x4	8x8	16x16	32x32	64x64
44	0.000017	0.000019	0.000020	0.000020	0.000020	0.000020	0.000020	0.00 %
50	0.000020	0.000020	0.000020	0.000020	0.000020	0.000020		0.00 %
144	0.000065	0.000062	0.000061	0.000061	0.000061	0.000061	0.000043	41.86 %
150	0.000043	0.000043	0.000043	0.000043	0.000043	0.000043		0.00 %

Замечания: При аналитическом решении прогибы w в центре пластины определяются по следующим формулам:

без учета деформаций поперечного сдвига

\[ w=\frac{12\cdot \left( {1-\nu^{2}} \right)\cdot a^{4}\cdot p}{E\cdot h^{3}}\cdot \left[ {\frac{5}{384}-\sum\limits_{m=1}^\infty {\frac{\sin \left( {\frac{m\cdot \pi }{2}} \right)\cdot \left( {4+m\cdot \pi \cdot th\left( {\frac{m\cdot \pi }{2}} \right)} \right)}{m^{5}\cdot \pi^{5}\cdot ch\left( {\frac{m\cdot \pi }{2}} \right)}} } \right] \quad или \] \[ w=\frac{192\cdot \left( {1-\nu^{2}} \right)\cdot a^{4}\cdot p}{\pi ^{6}\cdot E\cdot h^{3}}\cdot \sum\limits_{m=1}^\infty {\sum\limits_{n=1}^\infty {\left[ {\frac{1}{m\cdot n}\cdot \frac{1}{^{\left( {m^{2}+n^{2}} \right)^{2}}}\cdot \sin \left( {\frac{m\cdot \pi }{2}} \right)\cdot \sin \left( {\frac{n\cdot \pi }{2}} \right)} \right]} } ; \] \[ При \quad \nu \quad = 0.2 w\approx 0.004062\cdot \frac{a^{4}\cdot p}{D}, \quad где: \quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]

с учетом деформаций поперечного сдвига

\[w=\frac{12\cdot \left( {1-\nu^{2}} \right)\cdot a^{4}\cdot p}{E\cdot h^{3}}\cdot \left[ {\frac{5}{384}-\sum\limits_{m=1}^\infty {\frac{\sin \left( {\frac{m\cdot \pi }{2}} \right)\cdot \left( {4+m\cdot \pi \cdot th\left( {\frac{m\cdot \pi }{2}} \right)} \right)}{m^{5}\cdot \pi^{5}\cdot ch\left( {\frac{m\cdot \pi }{2}} \right)}+\frac{8-3\cdot \nu }{10\cdot \left( {1-\nu } \right)}\cdot \left( {\frac{h}{a}} \right)^{2}} \cdot \left( {\frac{1}{32}-\sum\limits_{m=1}^\infty {\frac{\sin \left( {\frac{m\cdot \pi }{2}} \right)}{m^{3}\cdot \pi^{3}\cdot ch\left( {\frac{m\cdot \pi }{2}} \right)}} } \right)} \right] \quad или \] \[ w=\frac{192\cdot \left( {1-\nu^{2}} \right)\cdot a^{4}\cdot p}{\pi ^{6}\cdot E\cdot h^{3}}\cdot \sum\limits_{m=1}^\infty {\sum\limits_{n=1}^\infty {\left[ {\frac{1}{m\cdot n}\cdot \frac{1}{^{\left( {m^{2}+n^{2}} \right)^{2}}}\cdot \left[ {1+\frac{\pi^{2}\cdot h^{2}}{5\cdot \left( {1-\nu } \right)\cdot a^{2}}\cdot \left( {m^{2}+n^{2}} \right)} \right]\cdot \sin \left( {\frac{m\cdot \pi }{2}} \right)\cdot \sin \left( {\frac{n\cdot \pi }{2}} \right)} \right]} } ; \] \[ При \quad \nu \quad = 0.2 \quad w\approx 0.004062\cdot \frac{a^{4}\cdot p}{D}\cdot \left[ {1+4.533786\cdot \left( {\frac{h}{a}} \right)^{2}} \right], \quad где: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]