Двухреберная балка под действием равномерно распределенных нагрузок, приложенных в плоскости ребер
Цель: Исследование распределения нормальных напряжений в двухреберной балке от действия равномерно распределенных нагрузок, приложенных в плоскости ребер.
Файл с исходными данными: 4_34.spr
Формулировка задачи: Двухреберная балка свободно опертая через торцевые идеальные диафрагмы абсолютно жесткие в их плоскости и абсолютно податливые из их плоскости находится под воздействием равномерно распределенных по линии вдоль ребер нагрузок q, приложенных в их плоскости. Определить нормальные напряжения σxi, действующие вдоль балки, в элементах ее конструкции в точках поперечного сечения i = 1, 4, 5, 6 для половины (l/2) и четверти (l/4) пролета балки при учете следующих допущений, принятых при выводе аналитического решения:
- Пренебрегаются изгибные деформации элементов конструкции балки из их плоскости;
- Принимается отсутствие перемещений в горизонтальной плоскости в направлении поперек балки на стыках ребер и полки;
- Не учитывается разность в напряжениях в конструктивных элементах балки на стыках ребер и полки.
Ссылки: А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. Строительная механика. Тонкостенные пространственные системы. — Москва: Стройиздат, 1983.
Исходные данные:
| E = 3·107 кПа | - модуль упругости; |
| μ = 0.15 | - коэффициент Пуассона; |
| δ = 0.1 м | - толщина ребер и полки; |
| b = 1.0 м | - высота ребер; |
| 2·b = 2.0 м | - расстояние между ребрами; |
| 4·b = 4.0 м | - ширина полки; |
| l = 7.85·b = 7.85 м | - длина балки; |
| q = 10.0 кН/м | - равномерно распределенная по линии вдоль ребер нагрузка. |
Конечноэлементная модель: Расчетная схема – система общего вида, элементы балки – 768 восьмиузловых элементов балки-стенки типа 27. Сетка конечных элементов разбита в направлении поперек балки с шагом 0.25 м и в направлении вдоль балки с шагом 0.2453125 м. Направление выдачи внутренних усилий сориентировано по направлению вдоль оси OX общей системы координат. Количество узлов в расчетной схеме – 2417.
Результаты решения в SCAD
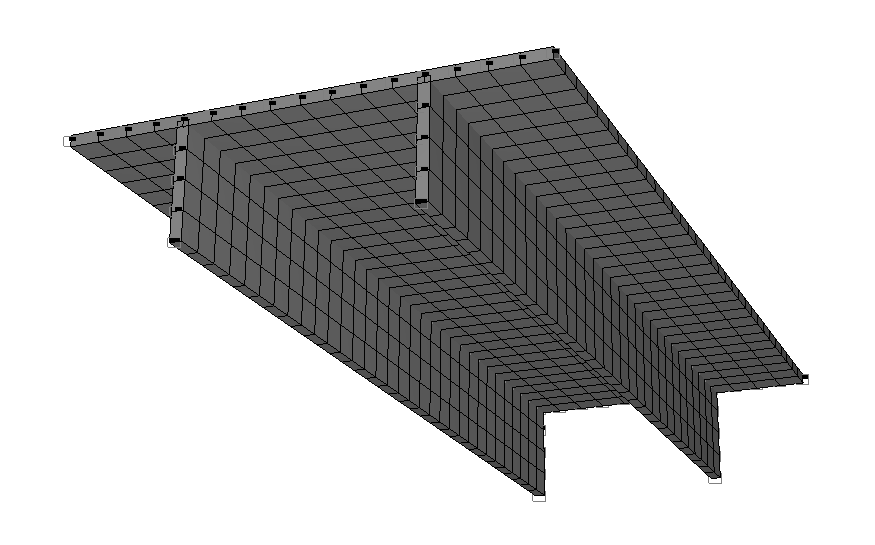
Расчетная схема
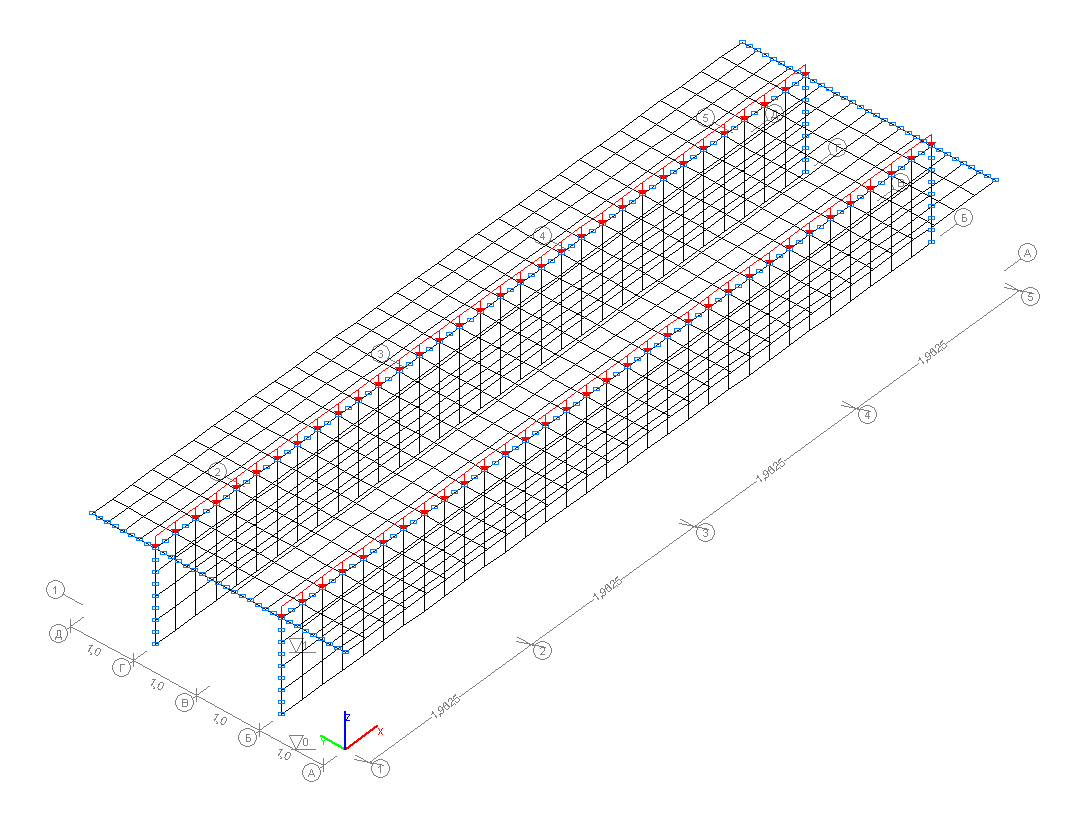
Расчетная схема
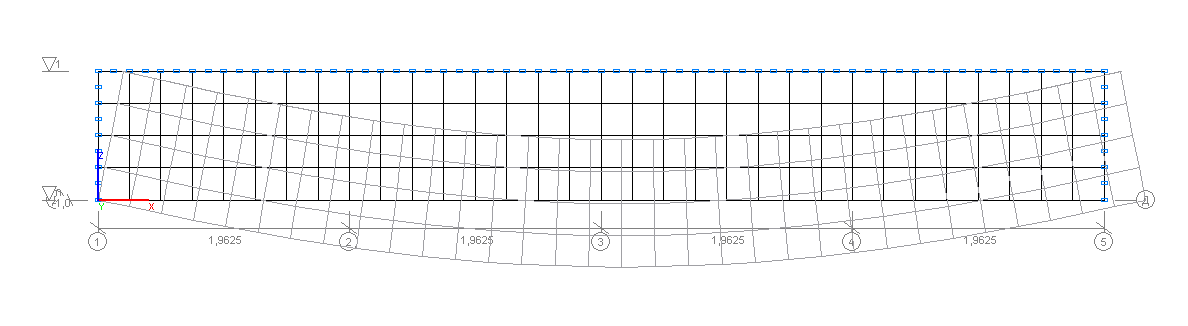
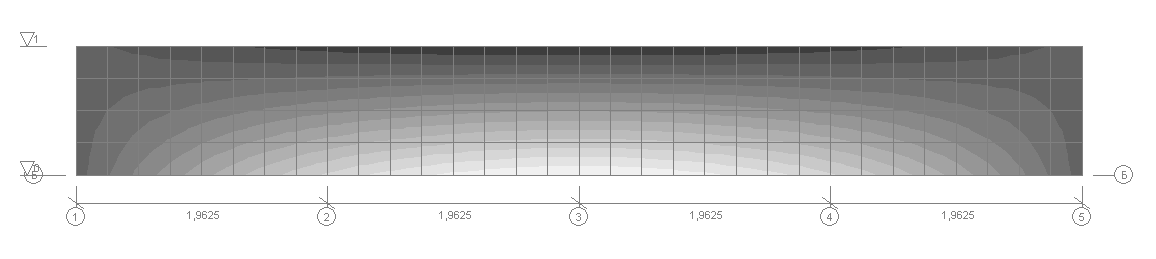
Деформированная схема
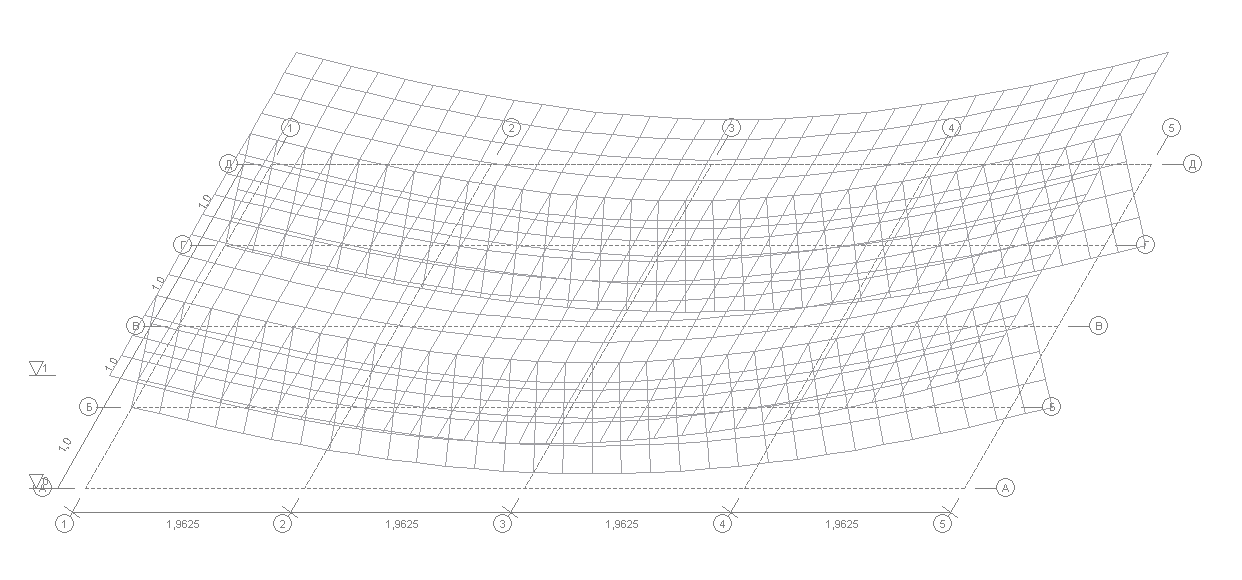
Деформированная схема
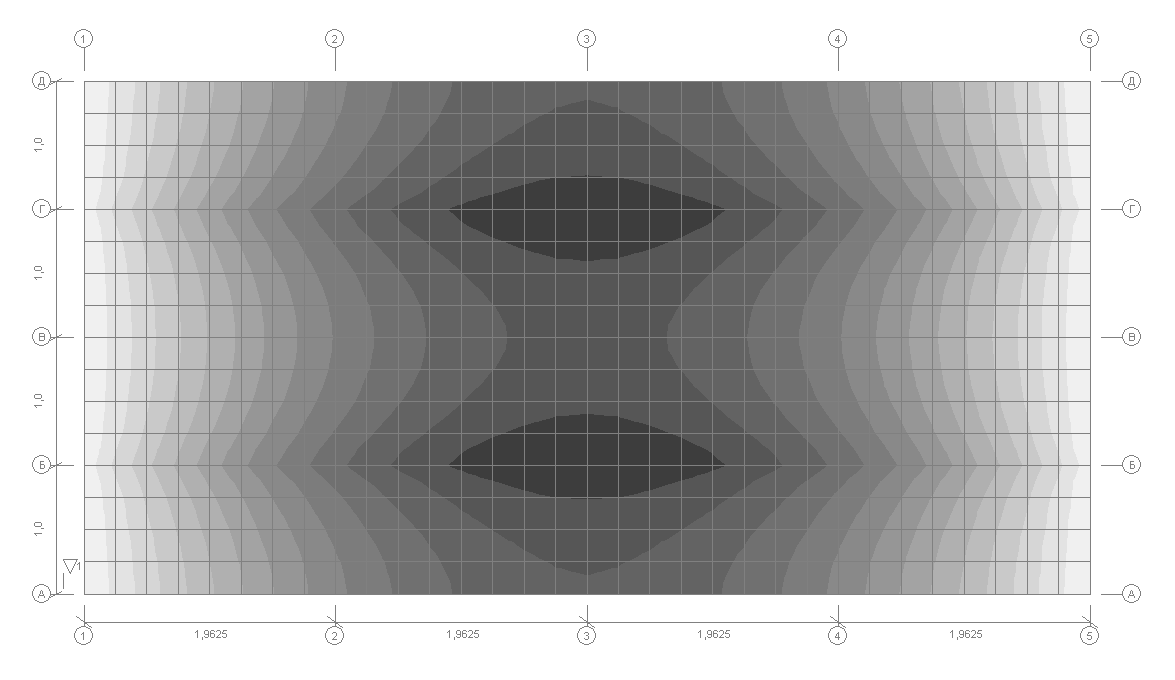

Значения нормальных напряжений в полке балки σxi (кН/м2)
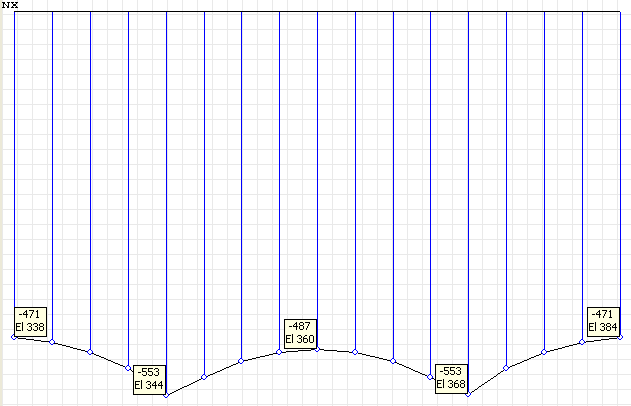
Эпюра нормальных напряжений в полке балки σxi (кН/м2) для поперечного сечения, расположенного в середине пролета балки-стенки l/2
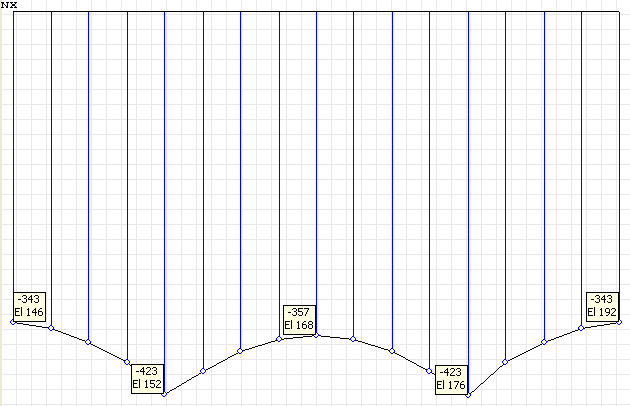
Эпюра нормальных напряжений в полке балки σxi (кН/м2) для поперечного сечения, расположенного в четверти пролета балки-стенки l/4

Значения нормальных напряжений в ребре балки σxi (кН/м2)
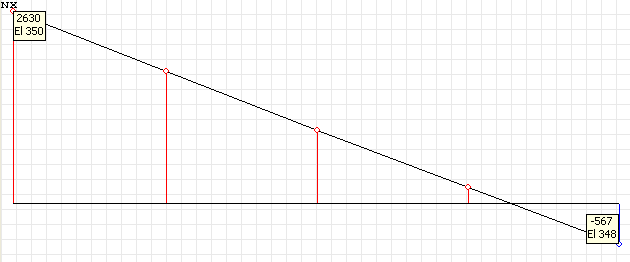
Эпюра нормальных напряжений в ребре балки σxi (кН/м2) для поперечного сечения, расположенного в середине пролета балки-стенки l/2
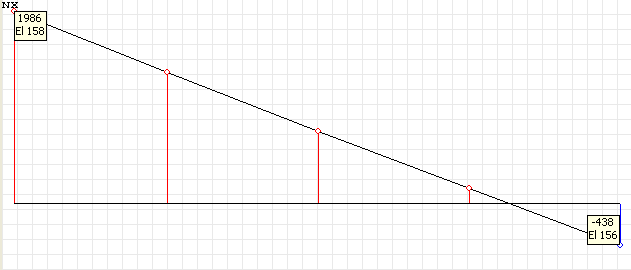
Эпюра нормальных напряжений в ребре балки σxi (кН/м2) для поперечного сечения, расположенного в четверти пролета балки-стенки l/4
Сравнение решений:
Нормальные напряжения σxi (кН/м2), действующие вдоль балки, в элементах ее конструкции в точках поперечного сечения i = 1, 4, 5, 6 для половины (l/2) и четверти (l/4) пролета балки
|
x, м |
l/2 = 3.925 |
l/4 = 1.9625 |
||||||
|---|---|---|---|---|---|---|---|---|
|
i |
1 |
4 |
5 |
6 |
1 |
4 |
5 |
6 |
|
Теория |
-564 |
2631 |
-472 |
-488 |
-435 |
1987 |
-345 |
-359 |
|
SCAD |
-567 |
2631 |
-471 |
-487 |
-439 |
1989 |
-344 |
-358 |
|
Отклонения, % |
0.53 |
0.00 |
0.21 |
0.20 |
0.92 |
0.10 |
0.29 |
0.28 |
Замечания: При аналитическом решении нормальные напряжения σxi (кН/м2), действующие вдоль балки, в элементах ее конструкции в точках поперечного сечения i = 1, 4, 5, 6 для половины (l/2) и четверти (l/4) пролета балки при учете семи гармоник неизвестных обобщенных перемещений для μ = 0.15 и l = 7.85·b могут быть вычислены по следующим формулам (А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. Строительная механика. Тонкостенные пространственные системы. — Москва: Стройиздат, 1983, стр. 383):
\[ \sigma_{x1} \left( {l/2} \right)=-5.641\cdot \frac{q}{\delta }; \quad \sigma_{x4} \left( {l/2} \right)=26.305\cdot \frac{q}{\delta }; \quad \sigma_{x5} \left( {l/2} \right)=-4.718\cdot \frac{q}{\delta }; \quad \sigma_{x6} \left( {l/2} \right)=-4.881\cdot \frac{q}{\delta }; \] \[ \sigma_{x1} \left( {l/4} \right)=-4.349\cdot \frac{q}{\delta }; \quad \sigma_{x4} \left( {l/4} \right)=19.873\cdot \frac{q}{\delta }; \quad \sigma_{x5} \left( {l/4} \right)=-3.450\cdot \frac{q}{\delta }; \quad \sigma_{x6} \left( {l/4} \right)=-3.587\cdot \frac{q}{\delta }; \]
