Криволинейная в плане коробчатая балка пролетного строения моста под действием сосредоточенной силы
Цель: Исследование распределения тангенциальных напряжений и вертикальных перемещений в криволинейной в плане коробчатой балки пролетного строения моста от действия вертикальной сосредоточенной силы, приложенной в середине пролета над внешней стенкой.
Имя файла с исходными данными: 4.35.SPR
Формулировка задачи: Коробчатая балка пролетного строения моста, продольная ось которой представляет в плане круговую кривую, свободно оперта через торцевые диафрагмы и нагружена сосредоточенной силой P, приложенной в середине пролета над внешней стенкой. Определить:
- распределение тангенциальных напряжений σx, действующих вдоль балки, на внешних поверхностях и в срединных плоскостях верхней и нижней полок по поперечному сечению в середине пролета;
- распределение тангенциальных напряжений σx, действующих вдоль балки, на внешней поверхности нижней полки вдоль продольной оси;
- распределение вертикальных перемещений w по нижним граням внешней и внутренней стенок вдоль продольной оси.
Ссылки: Worsak Kanok-Nukulchai, A simple and efficient finite element for general shell analysis, Int. J. num. meth. Engng, 14, 179-200 (1979); A.R.M. Fam and C. Turkstra, Model study of horizontally curved box girder, J. Engng Struct. Div., ASCE, 102, ST5, 1097-1108 (1976).
Исходные данные:
| E = 4.0·105 кПа | - модуль упругости; |
| ν = 0.36 | - коэффициент Пуассона; |
| R = 51.0 м | - радиус продольной оси балки; |
| θ = 45º | - центральный угол, содержащий половину пролета балки; |
| P = 20 кН | - сосредоточенная вертикальная сила, приложенная в середине пролета балки над внешней стенкой; |
| btf = 18.0 м | - ширина верхней полки; |
| ttf = 0.246 м | - толщина верхней полки; |
| bbf = 12.0 м | - ширина нижней полки; |
| tbf = 0.195 м | - толщина нижней полки; |
| hew = 2.5 м | - высота внешней стенки по внутренним поверхностям полок; |
| tew = 0.246 м | - толщина внешней стенки; |
| hiw = 2.5 м | - высота внутренней стенки по внутренним поверхностям полок; |
| tiw = 0.239 м | - толщина внутренней стенки; |
| ted = 0.239 м | - толщина торцевой диафрагмы; |
Конечно-элементная модель: Расчетная схема – система общего вида, элементы балки – 156 восьмиузловых элементов толстой оболочки для расчета по теории Рейсснера-Миндлина типа 150. Сетки конечных элементов верхней и нижней полок разбиты в радиальном направлении с шагом ~3.0 м и в тангенциальном направлении с шагом 7.5º, сетки конечных элементов внешней и внутренней стенок разбиты в вертикальном направлении с шагом ~2.7 м и в тангенциальном направлении – с шагом 7.5º. Направление выдачи внутренних усилий – радиально-тангенциальное. По узлам сопряжения элементов внешней и внутренней стенок с элементами торцевых диафрагм и нижней полки в вертикальном направлении установлены связи, обеспечивающие свободное опирание. Связи, предотвращающие смещения этих узлов в горизонтальной плоскости по радиальному направлению, моделируются 4 стержневыми элементами типа 4 с продольной жесткостью EF = 4.0·107 кН, конечные узлы которых закреплены по всем линейным степеням свободы. Геометрическая неизменяемость расчетной схемы в тангенциальном направлении обеспечивается за счет наложения связей по условиям ее симметрии. Количество узлов в расчетной схеме – 466.
Результаты решения в SCAD
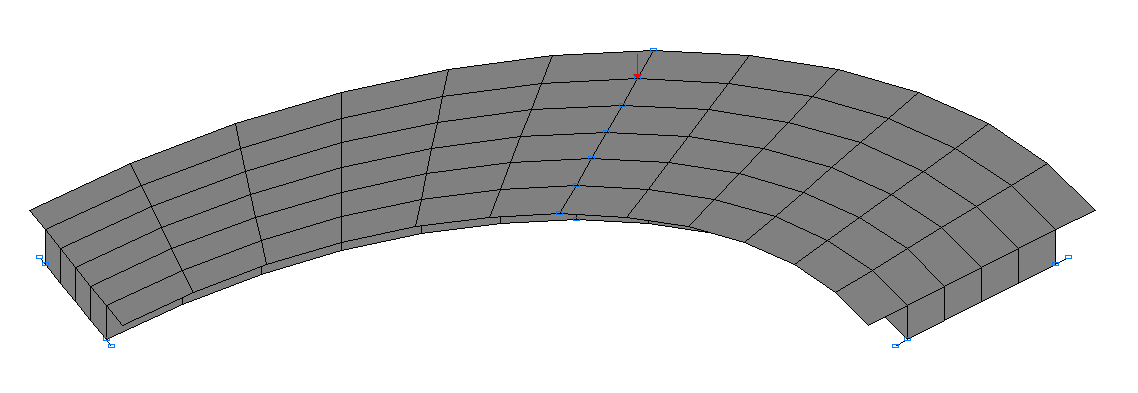
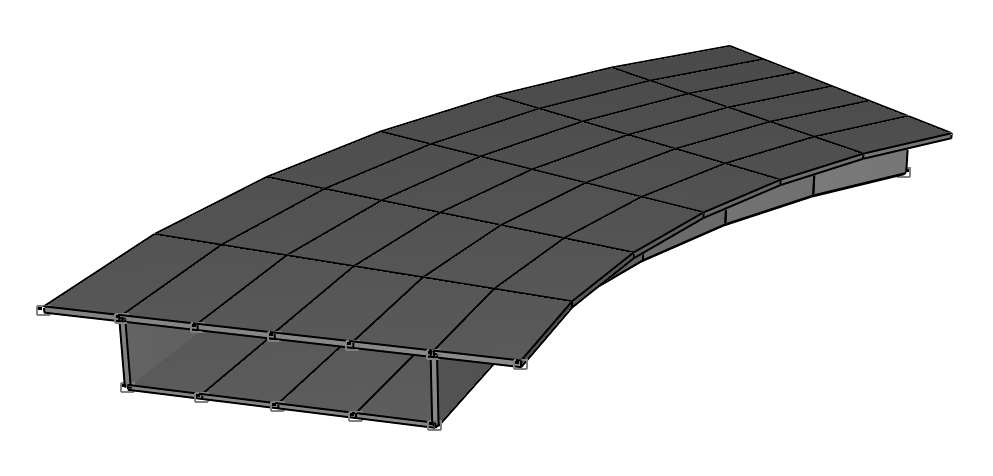
Расчетная схема
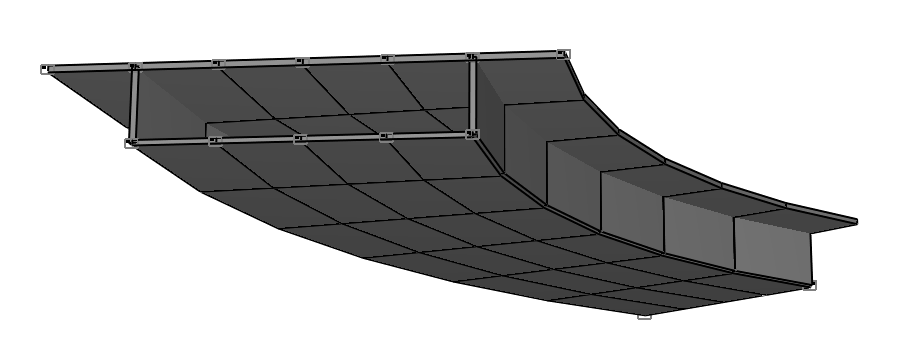
Деформированная схема
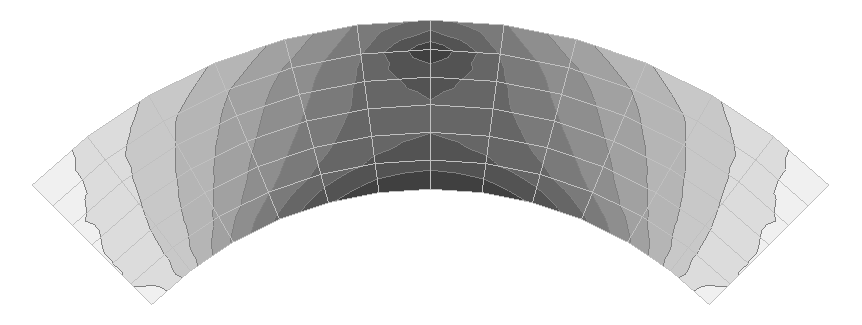

Значения тангенциальных напряжений σx, действующих вдоль балки, в срединной плоскости верхней полки (кН/м2)

Эпюра распределения тангенциальных напряжений σx, действующих вдоль балки, в срединной плоскости верхней полки по поперечному сечению в середине пролета (кН/м2)
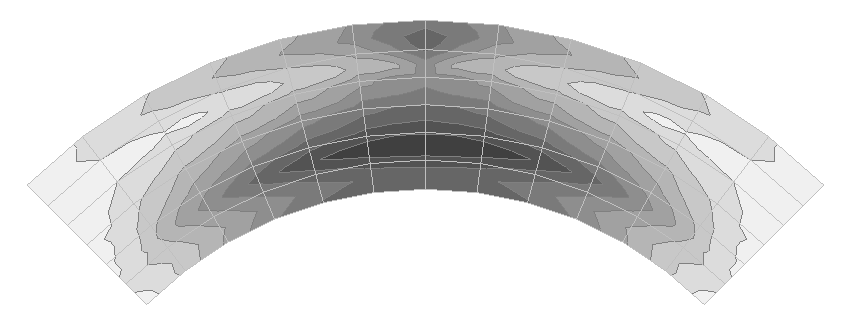
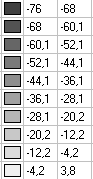
Значения тангенциальных напряжений σx, действующих вдоль балки, на внешней поверхности верхней полки (кН/м2)

Эпюра распределения тангенциальных напряжений σx, действующих вдоль балки, на внешней поверхности верхней полки по поперечному сечению в середине пролета (кН/м2)
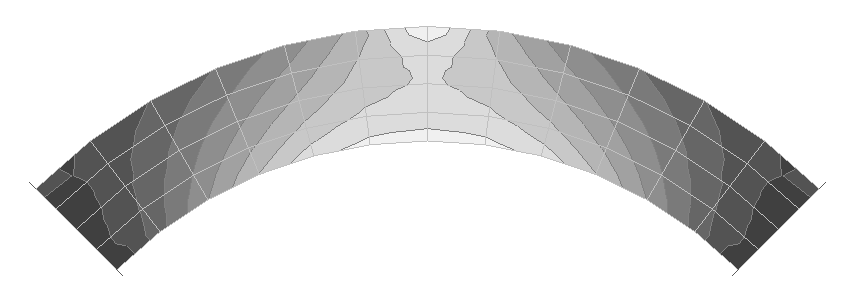
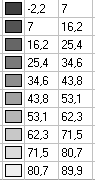
Значения тангенциальных напряжений σx, действующих вдоль балки, в срединной плоскости нижней полки (кН/м2)

Эпюра распределения тангенциальных напряжений σx, действующих вдоль балки, в срединной плоскости нижней полки по поперечному сечению в середине пролета (кН/м2)


Значения тангенциальных напряжений σx, действующих вдоль балки, на внешней поверхности нижней полки (кН/м2)

Эпюра распределения тангенциальных напряжений σx, действующих вдоль балки, на внешней поверхности нижней полки по поперечному сечению в середине пролета (кН/м2)
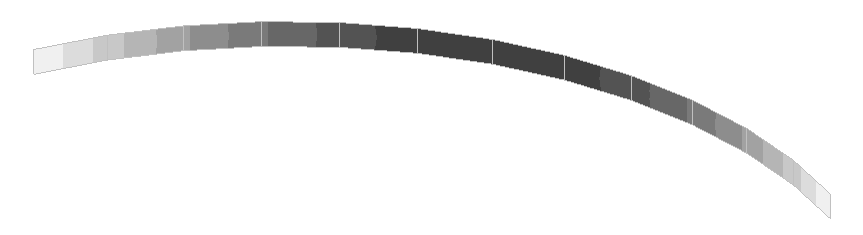

Значения вертикальных перемещений w внешней стенки (м)
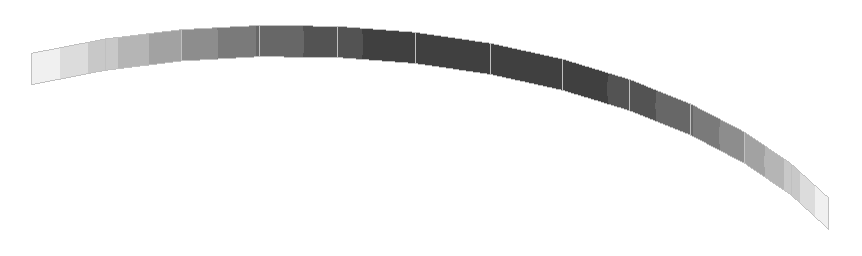

Значения вертикальных перемещений w внутренней стенки (м)
Сравнение решений:
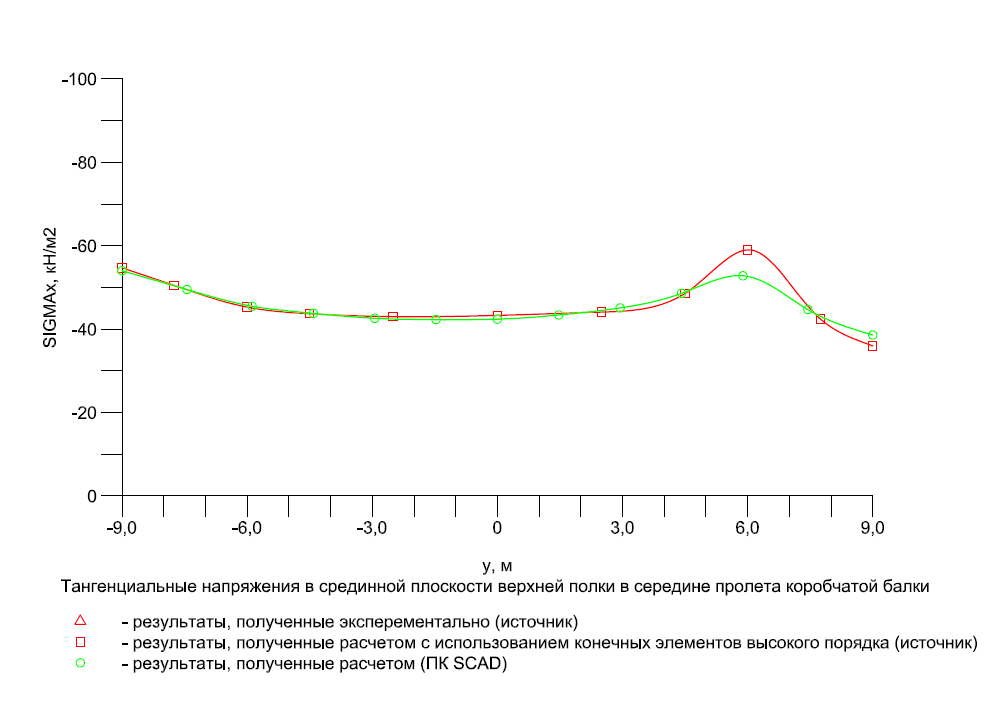
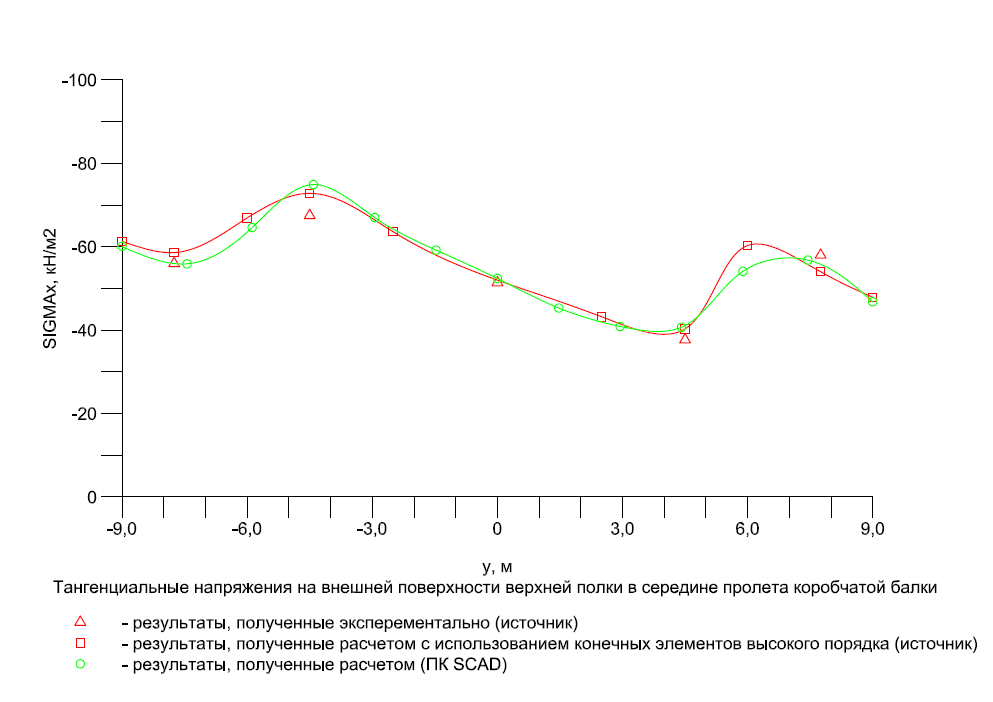
|
y |
Эксперимент |
SCAD |
Отклонения, % |
|---|---|---|---|
|
-7.75 |
-56.0 |
-55.97 |
0.05 |
|
-4.50 |
-67.5 |
-74.82 |
10.84 |
|
0.00 |
-51.4 |
-52.40 |
1.95 |
|
4.50 |
-37.7 |
-41.10 |
9.02 |
|
7.75 |
-58.0 |
-55.79 |
3.81 |
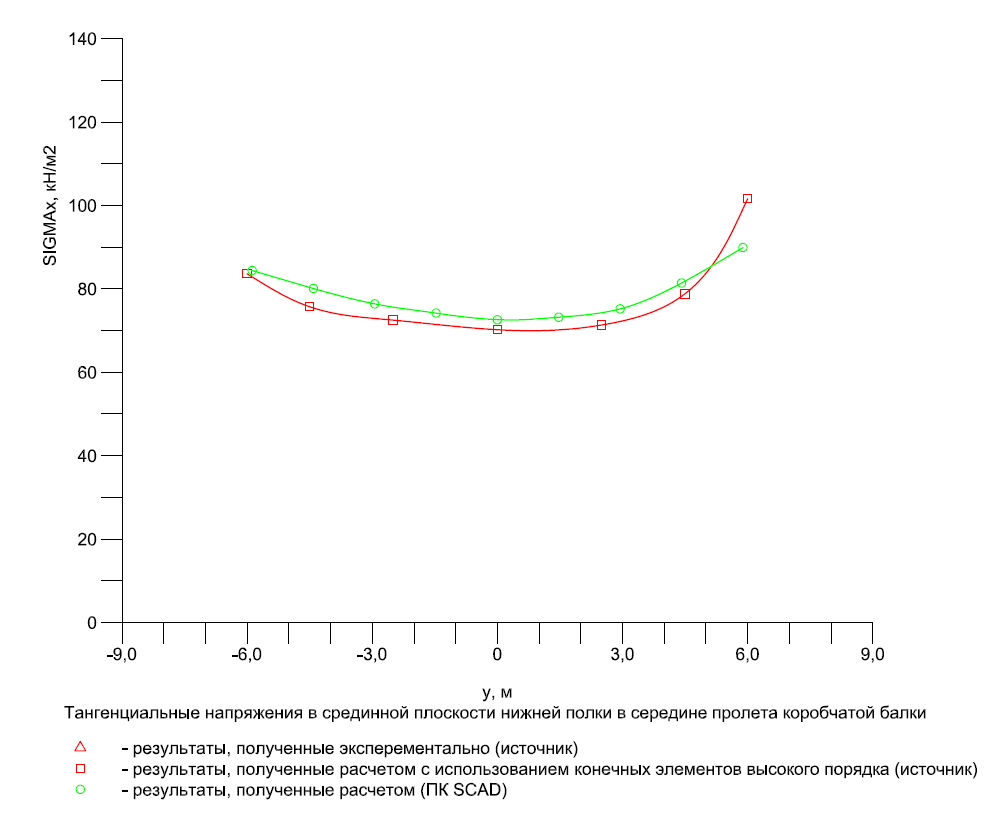
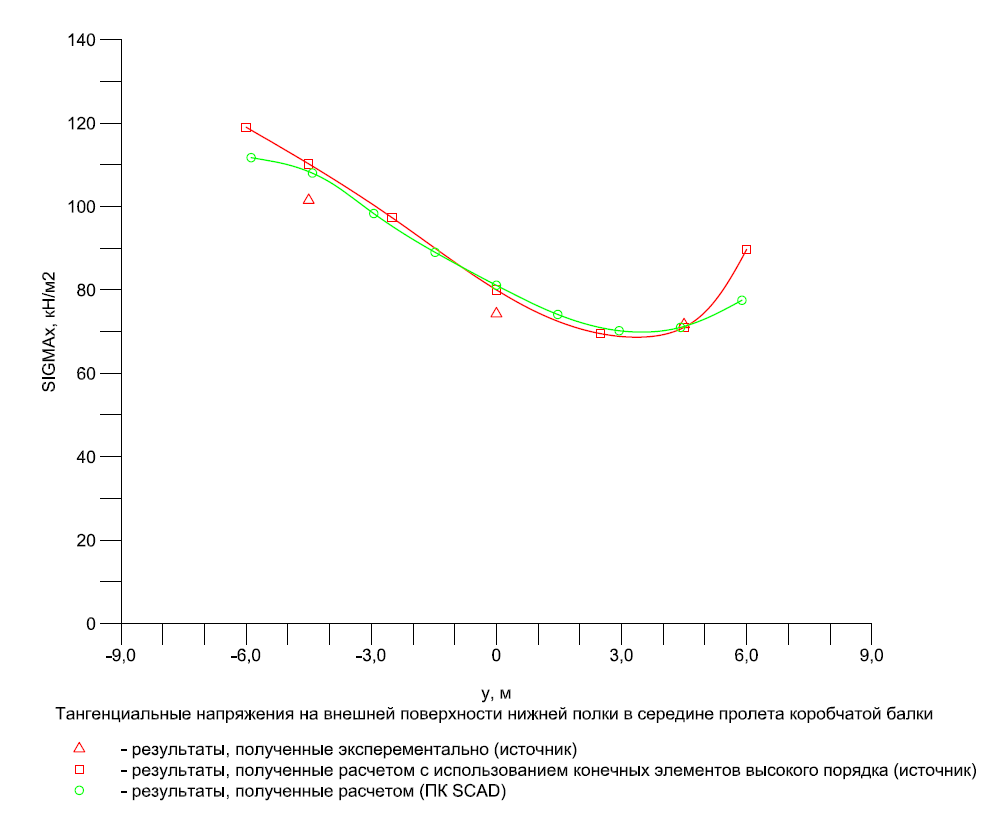
|
y |
Эксперимент |
SCAD |
Отклонения, % |
|---|---|---|---|
|
-4.50 |
101.5 |
108.38 |
6.78 |
|
0.00 |
74.3 |
81.10 |
9.15 |
|
4.50 |
71.7 |
71.23 |
0.66 |
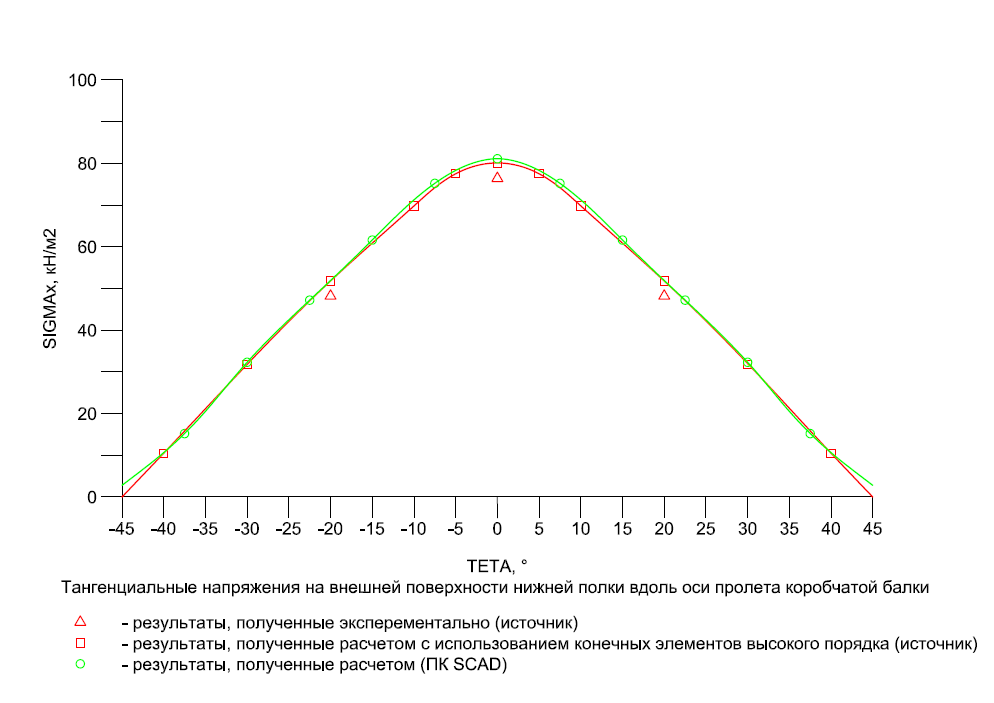
|
θ |
Эксперимент |
SCAD |
Отклонения, % |
|---|---|---|---|
|
-20 |
48.2 |
51.91 |
7.70 |
|
0 |
76.4 |
81.10 |
6.15 |
|
20 |
48.2 |
51.91 |
7.70 |
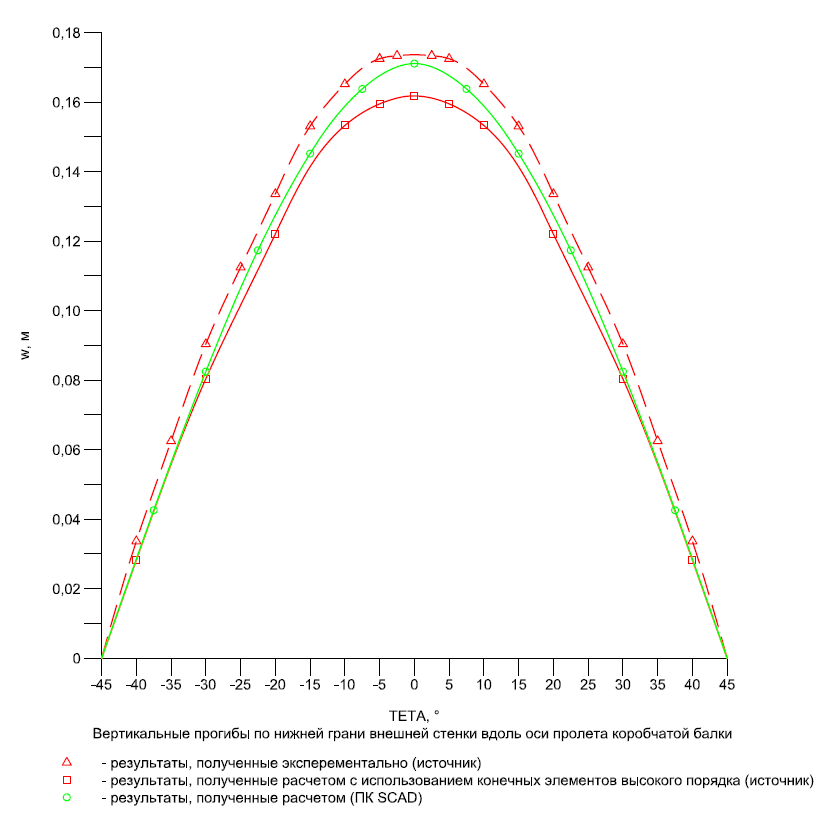
|
θ |
Эксперимент |
SCAD |
Отклонения, % |
|---|---|---|---|
|
-35 |
0.0625 |
0.05631 |
9.90 |
|
-30 |
0.0904 |
0.08250 |
8.74 |
|
-25 |
0.1125 |
0.10650 |
5.33 |
|
-20 |
0.1336 |
0.12750 |
4.57 |
|
-15 |
0.1531 |
0.14520 |
5.16 |
|
-10 |
0.1652 |
0.15887 |
3.83 |
|
-5 |
0.1725 |
0.16762 |
2.83 |
|
-2.5 |
0.1734 |
0.17016 |
1.87 |
|
2.5 |
0.1734 |
0.17016 |
1.87 |
|
5 |
0.1725 |
0.16762 |
2.83 |
|
10 |
0.1652 |
0.15887 |
3.83 |
|
15 |
0.1531 |
0.14520 |
5.16 |
|
20 |
0.1336 |
0.12750 |
4.57 |
|
25 |
0.1125 |
0.10650 |
5.33 |
|
30 |
0.0904 |
0.08250 |
8.74 |
|
35 |
0.0625 |
0.05631 |
9.90 |
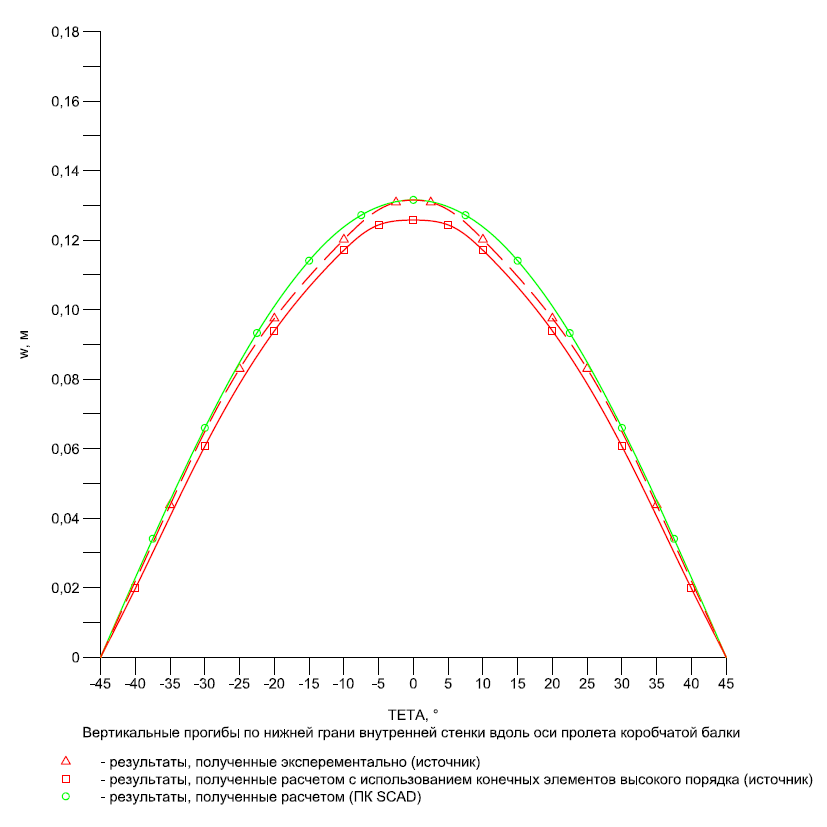
|
θ |
Эксперимент |
SCAD |
Отклонения, % |
|---|---|---|---|
|
-35 |
0.0438 |
0.04510 |
2.97 |
|
-25 |
0.0830 |
0.08487 |
2.25 |
|
-20 |
0.0975 |
0.10101 |
3.60 |
|
-10 |
0.1202 |
0.12384 |
3.03 |
|
-2.5 |
0.1309 |
0.13108 |
0.14 |
|
2.5 |
0.1309 |
0.13108 |
0.14 |
|
10 |
0.1202 |
0.12384 |
3.03 |
|
20 |
0.0975 |
0.10101 |
3.60 |
|
25 |
0.0830 |
0.08487 |
2.25 |
|
35 |
0.0438 |
0.04510 |
2.97 |
