Цилиндрическая оболочка со свободно опертыми торцами под равномерным внутренним давлением

Цель: Определение напряженно-деформированного состояния цилиндрической оболочки со свободно опертыми торцами от воздействия внутреннего давления.

Файл с исходными данными: 4_31.spr

Формулировка задачи: Цилиндрическая тонкостенная оболочка, свободно опертая по торцам, находится под воздействием внутреннего равномерного давления p. Определить изгибающие моменты и продольные силы, действующие на срединной поверхности оболочки в меридиональном M_x, N_x и окружном M_φ, N_φ направлениях, а также радиальные перемещения w для поперечного сечения, расположенного в середине пролета.

Ссылки: С.П. Тимошенко. Пластинки и оболочки. — Москва: ОГИЗ. Гостехиздат, 1948.

Исходные данные:

E = 2.1·108 кПа	- модуль упругости;
ν = 0.3	- коэффициент Пуассона;
h = 0.02 м	- толщина оболочки;
a = 10.0 м	- радиус срединной поверхности оболочки;
l = 2.0 м	- длина оболочки;
p = 10.0 кПа	- внутреннее давление.

 

Конечноэлементная модель: Расчетная  схема – система общего вида, элементы оболочки – 9216 четырехузловых элементов типа 44. Сетка конечных элементов разбита с шагом 0.0625м в меридиональном направлении и с шагом 1.25º в окружном направлении. Обеспечение граничных условий на свободно опертых торцах достигается за счет наложения связей по направлениям углового и линейных  перемещений в их плоскости. Количество узлов в расчетной схеме – 9504.

Результаты решения в SCAD

Расчетная  и деформированная схемы

 
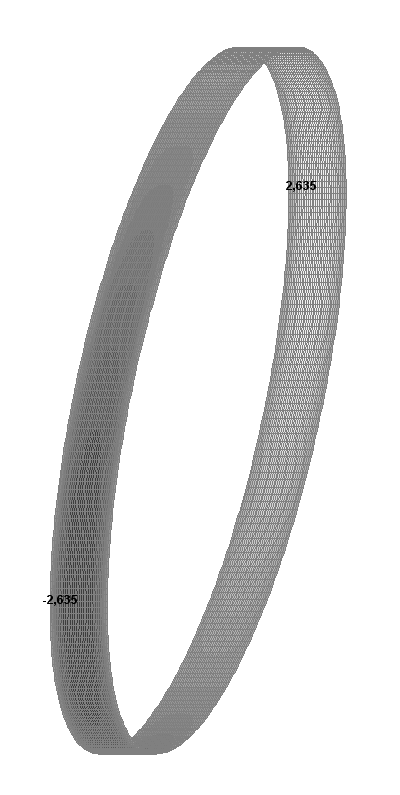
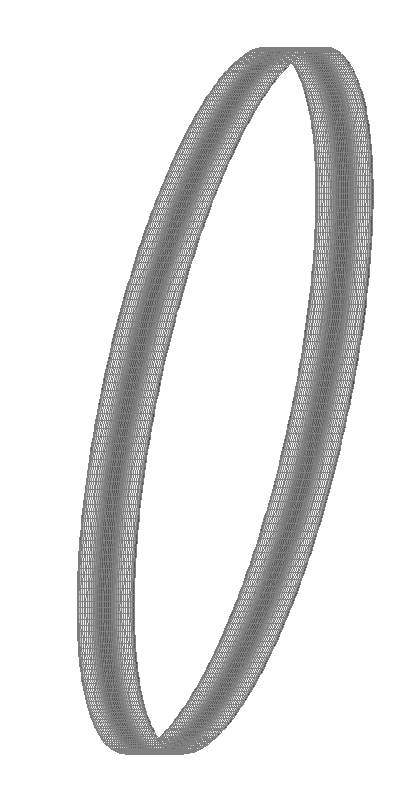
Значения радиальных перемещений w (мм)

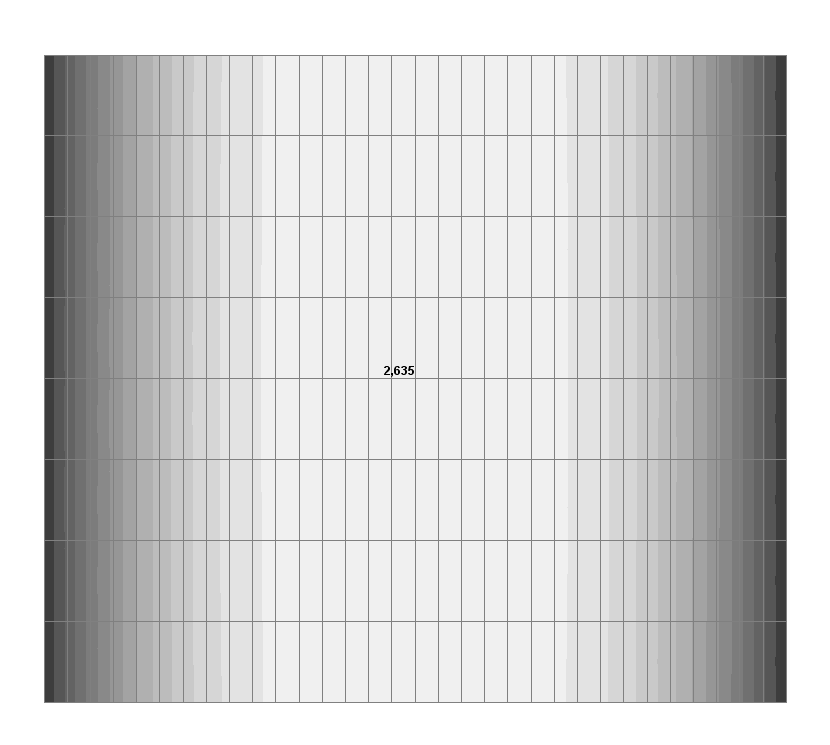
Значения радиальных перемещений w (мм) для фрагмента схемы из участка в области горизонтального диаметра с центральным углом 5.00º

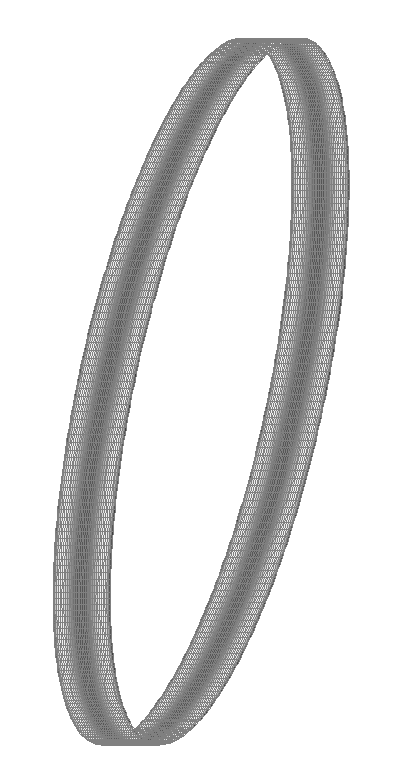
Значения изгибающих моментов, действующих на срединной поверхности оболочки в меридиональном направлении M_x (кН•м/м)

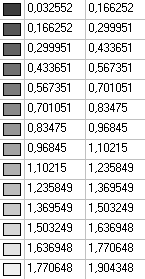
Значения изгибающих моментов, действующих на срединной поверхности оболочки в меридиональном направлении M_x (кН∙м/м)

для фрагмента схемы из участка в области горизонтального диаметра с центральным углом 5.00º

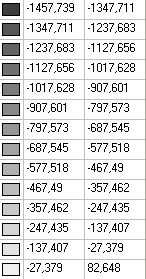
Значения изгибающих моментов, действующих на срединной поверхности оболочки в окружном направлении M_φ (кН•м/м)

Значения изгибающих моментов, действующих на срединной поверхности оболочки в окружном направлении M_φ (кН•м/м) для фрагмента схемы из участка в области горизонтального диаметра с центральным углом 5.00º

Значения продольных сил, действующих на срединной поверхности оболочки в меридиональном направлении N_x (кН/м²)

Значения продольных сил, действующих на срединной поверхности оболочки в меридиональном направлении N_x (кН/м²) для фрагмента схемы из участка в области горизонтального диаметра с центральным углом 5.00º

Значения продольных сил, действующих на срединной поверхности оболочки в окружном направлении N_φ (кН/м²)

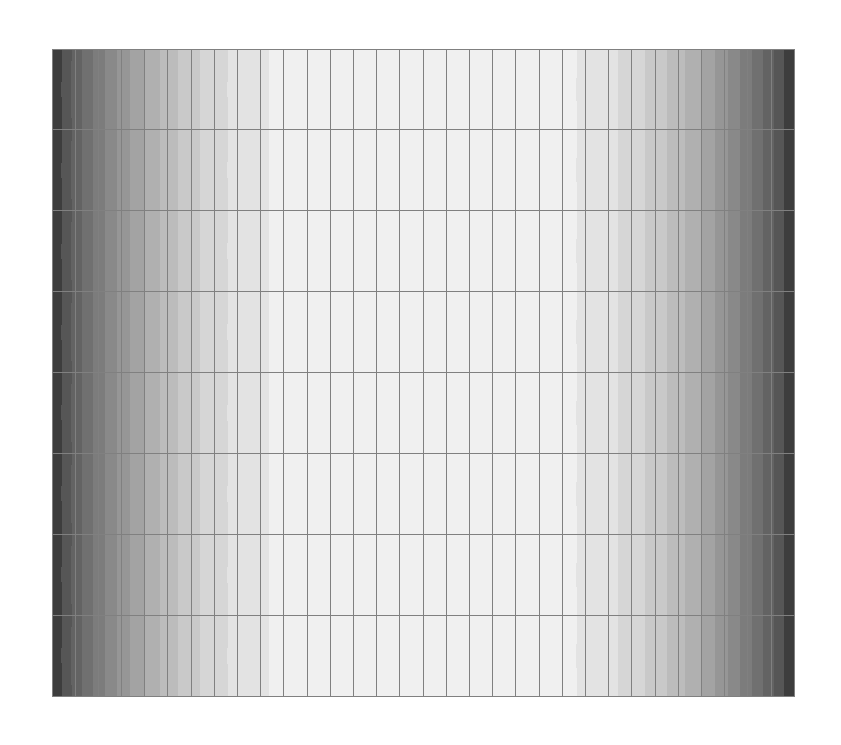
Значения продольных сил, действующих на срединной поверхности оболочки в окружном направлении N_φ (кН/м²) для фрагмента схемы из участка в области горизонтального диаметра с центральным углом 5.00º

 

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
w(l/2), мм	2.640	2.635	0.19
Mx(l/2), кН•м/м	0.178969	0.180453	0.83
Mφ(l/2), кН•м/м	0.053691	0.054136	0.83
Nx(l/2), кН/м	0.000	8.238•0.02 = 0.165	-
Nφ(l/2), кН/м	1108.655	55346.398∙0.02 = 1106.928	0.16

Замечания: При аналитическом решении изгибающие моменты и продольные силы, действующие на срединной поверхности оболочки в меридиональном M_x, N_x и окружном M_φ, N_φ направлениях, а также радиальные перемещения w для поперечного сечения, расположенного в половине пролета, могут быть вычислены по следующим формулам (С.П. Тимошенко. Пластинки и оболочки. — Москва: ОГИЗ. Гостехиздат, 1948, стр. 377):

\[ w=\frac{p\cdot l^{4}}{64\cdot D\cdot \alpha^{4}}\cdot \left( {1-\frac{2\cdot \cos \left( \alpha \right)\cdot ch\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}} \right)=\frac{p\cdot a^{2}}{E\cdot h}\cdot \left( {1-\frac{2\cdot \cos \left( \alpha \right)\cdot ch\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}} \right); \] \[ M_{x} =\frac{p\cdot l^{2}}{4\cdot \alpha^{2}}\cdot \frac{\sin \left( \alpha \right)\cdot sh\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}=\frac{p\cdot a\cdot h}{\sqrt {3\cdot \left( {1-\nu^{2}} \right)} }\cdot \frac{\sin \left( \alpha \right)\cdot sh\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}; \] \[ M_{\phi } =\nu \cdot M_{x} =\frac{p\cdot a\cdot h\cdot \nu }{\sqrt {3\cdot \left( {1-\nu^{2}} \right)} }\cdot \frac{\sin \left( \alpha \right)\cdot sh\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}; \] \[ \quad N_{x} =0; \quad N_{\phi } =-\frac{E\cdot h}{a}\cdot w=-p\cdot a\cdot \left( {1-\frac{2\cdot \cos \left( \alpha \right)\cdot ch\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}} \right), \quadгде: \]\[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad \beta =\sqrt[4]{\frac{3\cdot \left( {1-\nu^{2}} \right)}{a^{2}\cdot h^{2}}}, \quad \alpha =\frac{\beta \cdot l}{2}. \]