Цилиндрический вертикальный резервуар со стенкой постоянной толщины с плоским днищем под действием внутреннего давления жидкости
Цель: Определение напряженно-деформированного состояния цилиндрического вертикального резервуара со стенкой постоянной толщины, защемленного в плоское днище, от воздействия внутреннего давления жидкости, линейно изменяющегося по высоте.
Файл с исходными данными: 4_32.spr
Формулировка задачи: Цилиндрический вертикальный резервуар со стенкой постоянной толщины защемлен в плоское днище и находится под воздействием линейно изменяющегося по высоте внутреннего давления жидкости с объемным весом γ. Определить изгибающие моменты и продольные силы, действующие на срединной поверхности стенки резервуара в меридиональном Mx, Nx и окружном Mφ, Nφ направлениях, а также радиальные перемещения w стенки резервуара.
Ссылки: С.П. Тимошенко. Пластинки и оболочки. — Москва: ОГИЗ. Гостехиздат, 1948.
Исходные данные:
| E = 2.1·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| h = 0.01 м | - толщина стенки резервуара; |
| a = 5.0 м | - радиус срединной поверхности стенки резервуара; |
| d = 5.0 м | - высота резервуара; |
| γ = 10.0 кН/м3 | - объемный вес жидкости, находящейся в резервуаре. |
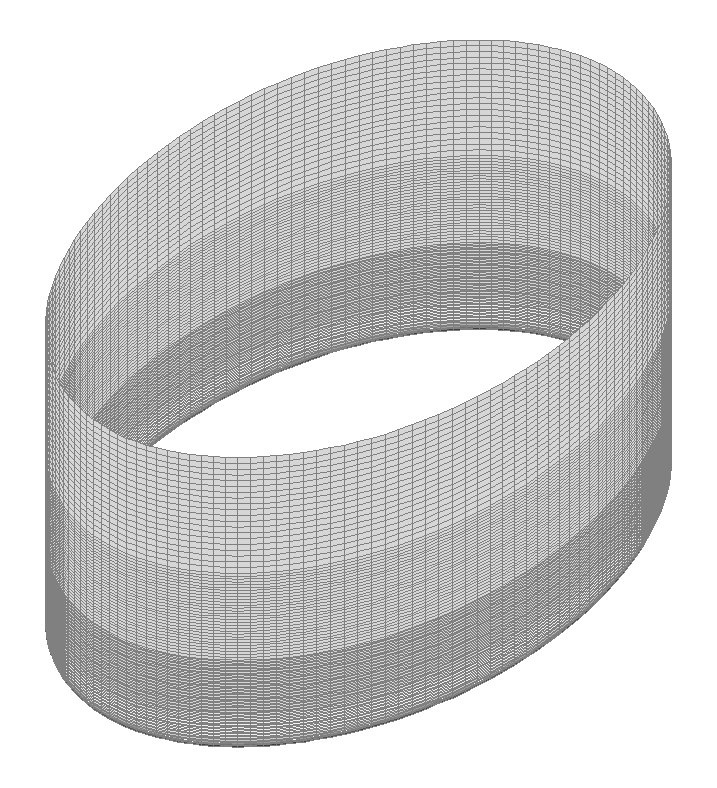
Конечноэлементная модель: Расчетная схема – система общего вида, элементы оболочки – 15840 четырехузловых элементов типа 44. Сетка конечных элементов разбита в меридиональном направлении с шагом 0.025 м на высоте x от днища с 0.0 м до 1.5 м, с шагом 0.050 м на высоте x от днища с 1.5 м до 3.0 м, с шагом 0.100 м на высоте x от днища с 3.0 м до 5.0 м и в окружном направлении с шагом 2.5º. Обеспечение граничных условий в уровне защемления в днище достигается за счет наложения связей по всем направлениям угловых и линейных перемещений. Количество узлов в расчетной схеме – 15984.
Результаты решения в SCAD

Расчетная схема
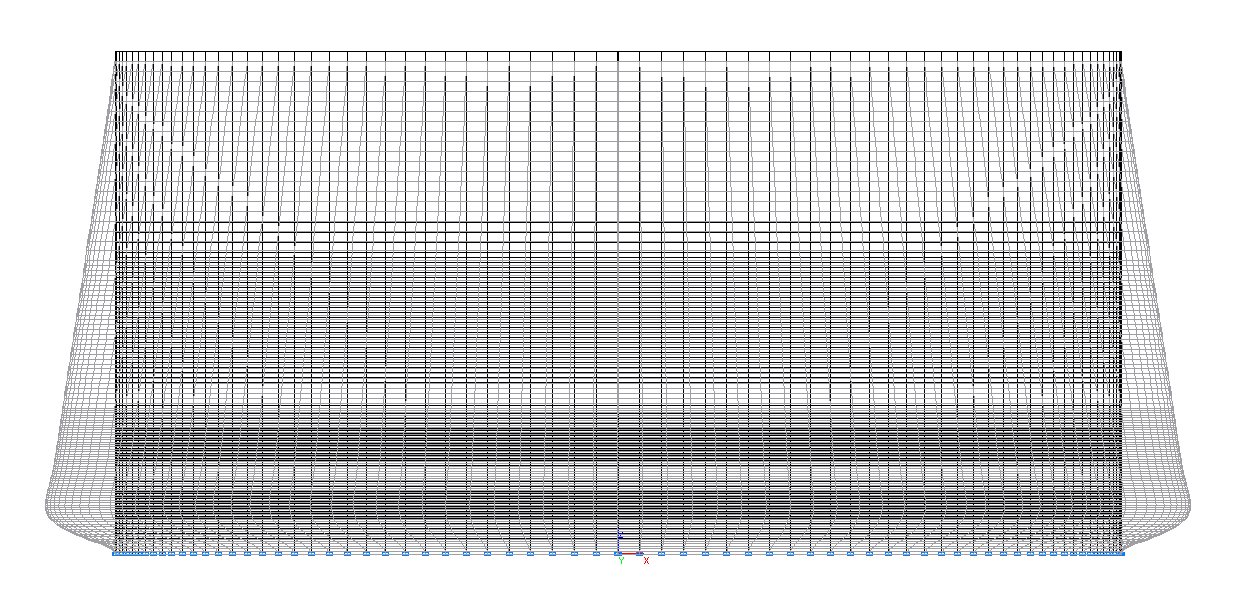
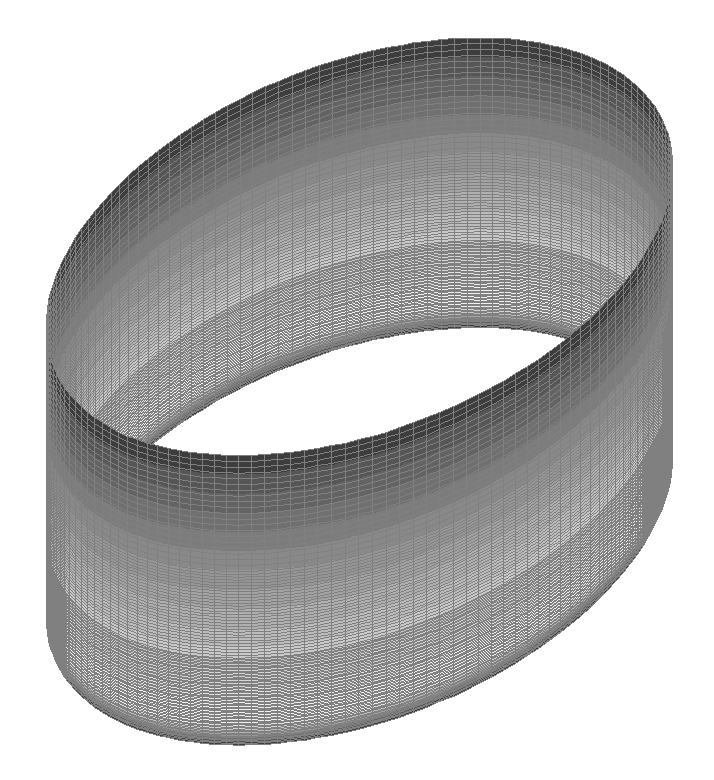
Деформированная схема

Деформированная схема
Значения радиальных перемещений w (мм)
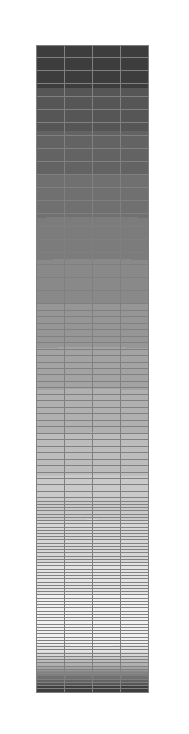

Значения радиальных перемещений w (мм) для фрагмента схемы из участка с центральным углом 10.0º

Значения изгибающих моментов, действующих на срединной поверхности стенки резервуара в меридиональном направлении Mx (кН∙м/м)

Значения изгибающих моментов, действующих на срединной поверхности стенки резервуара в меридиональном направлении Mx (кН∙м/м) для фрагмента схемы из участка с центральным углом 10.0º
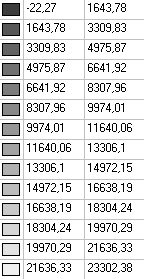
Значения продольных сил, действующих на срединной поверхности стенки резервуара в окружном направлении Nφ (кН/м2)


Значения продольных сил, действующих на срединной поверхности стенки резервуара в окружном направлении Nφ (кН/м2) для фрагмента схемы из с центральным углом 10.0º
Сравнение решений:
|
x, м |
w, мм |
Mx, кН∙м/м |
Nφ, кН/м |
||||||
|---|---|---|---|---|---|---|---|---|---|
|
Теория |
SCAD |
Откло-нения, % |
Теория |
SCAD |
Отклонения, % |
Теория |
SCAD |
Откло-нения, % |
|
|
0.000 |
0.000 |
0.000 |
- |
-0.7302 |
-0.7267 |
0.48 |
0.00 |
-22.27∙0.01 = -0.22 |
- |
|
0.025 |
0.011 |
0.011 |
0.00 |
-0.5321 |
-0.5253 |
1.28 |
4.52 |
432.34∙0.01 = 4.32 |
4.42 |
|
0.050 |
0.039 |
0.039 |
0.00 |
-0.3644 |
-0.3564 |
2.20 |
16.33 |
1612.89∙0.01 = 16.13 |
1.22 |
|
0.075 |
0.079 |
0.078 |
1.27 |
-0.2256 |
-0.2179 |
3.41 |
33.15 |
3285.96∙0.01 = 32.86 |
0.87 |
|
0.100 |
0.126 |
0.125 |
0.79 |
-0.1134 |
-0.1069 |
5.73 |
53.08 |
5261.88∙0.01 = 52.62 |
0.87 |
|
0.125 |
0.178 |
0.176 |
1.12 |
-0.0252 |
-0.0204 |
- |
74.59 |
7388.51∙0.01 = 73.89 |
0.94 |
|
0.150 |
0.230 |
0.227 |
1.30 |
0.0419 |
0.0448 |
- |
96.46 |
9547.11∙0.01 = 95.47 |
1.03 |
|
0.175 |
0.280 |
0.277 |
1.07 |
0.0907 |
0.0918 |
1.21 |
117.78 |
11648.07∙0.01 = 116.48 |
1.10 |
|
0.200 |
0.328 |
0.324 |
1.22 |
0.1241 |
0.1235 |
0.48 |
137.88 |
13626.65∙0.01 = 136.27 |
1.17 |
|
0.225 |
0.372 |
0.367 |
1.34 |
0.1448 |
0.1428 |
1.38 |
156.30 |
15439.08∙0.01 = 154.39 |
1.22 |
|
0.250 |
0.411 |
0.406 |
1.22 |
0.1550 |
0.1520 |
1.94 |
172.76 |
17058.39∙0.01 = 170.58 |
1.26 |
|
0.275 |
0.445 |
0.440 |
1.12 |
0.1572 |
0.1535 |
2.35 |
187.11 |
18471.73∙0.01 = 184.72 |
1.28 |
|
0.300 |
0.475 |
0.468 |
1.47 |
0.1532 |
0.1491 |
2.68 |
199.32 |
19676.68∙0.01 = 196.77 |
1.28 |
|
0.325 |
0.499 |
0.492 |
1.40 |
0.1447 |
0.1405 |
2.90 |
209.44 |
20678.89∙0.01 = 206.79 |
1.27 |
|
0.350 |
0.518 |
0.512 |
1.16 |
0.1332 |
0.1291 |
3.08 |
217.60 |
21489.82∙0.01 = 214.90 |
1.24 |
|
0.375 |
0.533 |
0.527 |
1.13 |
0.1198 |
0.1160 |
3.17 |
223.93 |
22124.83∙0.01 = 221.25 |
1.20 |
|
0.400 |
0.544 |
0.538 |
1.10 |
0.1054 |
0.1021 |
3.13 |
228.64 |
22601.65∙0.01 = 226.02 |
1.15 |
|
0.425 |
0.552 |
0.546 |
1.09 |
0.0909 |
0.0881 |
3.08 |
231.90 |
22939.13∙0.01 = 229.39 |
1.08 |
|
0.450 |
0.557 |
0.551 |
1.08 |
0.0767 |
0.0745 |
2.87 |
233.93 |
23156.28∙0.01 = 231.56 |
1.01 |
|
0.475 |
0.559 |
0.554 |
0.89 |
0.0633 |
0.0617 |
2.53 |
234.90 |
23271.56∙0.01 = 232.72 |
0.93 |
|
0.500 |
0.560 |
0.555 |
0.89 |
0.0510 |
0.0500 |
1.96 |
235.01 |
23302.38∙0.01 = 233.02 |
0.85 |
|
0.550 |
0.555 |
0.552 |
0.54 |
0.0303 |
0.0302 |
0.33 |
233.29 |
23172.87∙0.01 = 231.73 |
0.67 |
|
0.600 |
0.547 |
0.545 |
0.37 |
0.0148 |
0.0155 |
4.73 |
229.89 |
22875.52∙0.01 = 228.76 |
0.49 |
|
0.650 |
0.537 |
0.535 |
0.37 |
0.0043 |
0.0055 |
- |
225.66 |
22490.85∙0.01 = 224.91 |
0.33 |
|
0.700 |
0.527 |
0.526 |
0.19 |
-0.0022 |
-0.0008 |
- |
221.17 |
22074.31∙0.01 = 220.74 |
0.19 |
|
0.750 |
0.516 |
0.516 |
0.00 |
-0.0055 |
-0.0042 |
- |
216.79 |
21660.60∙0.01 = 216.61 |
0.08 |
|
0.800 |
0.506 |
0.506 |
0.00 |
-0.0067 |
-0.0055 |
- |
212.70 |
21268.60∙0.01 = 212.69 |
0.00 |
|
0.850 |
0.498 |
0.498 |
0.00 |
-0.0066 |
-0.0056 |
- |
208.97 |
20906.05∙0.01 = 209.06 |
0.04 |
|
0.900 |
0.490 |
0.490 |
0.00 |
-0.0057 |
-0.0049 |
- |
205.59 |
20573.53∙0.01 = 205.74 |
0.07 |
|
0.950 |
0.482 |
0.483 |
0.21 |
-0.0045 |
-0.0039 |
- |
202.53 |
20267.56∙0.01 = 202.68 |
0.07 |
|
1.000 |
0.475 |
0.476 |
0.21 |
-0.0032 |
-0.0028 |
- |
199.71 |
19982.79∙0.01 = 199.83 |
0.06 |
Замечания: При аналитическом решении изгибающие моменты и продольные силы, действующие на срединной поверхности стенки резервуара в меридиональном Mx, Nx и окружном Mφ, Nφ направлениях, а также радиальные перемещения w стенки резервуара могут быть вычислены по следующим формулам (С.П. Тимошенко, Пластинки и оболочки. — Москва: ОГИЗ. Гостехиздат, 1948, стр. 388):
\[ w=\frac{\gamma \cdot a^{2}\cdot d}{E\cdot h}\cdot \left( {1-\frac{x}{d}-e^{-\beta \cdot x}\cdot \left( {\cos \left( {\beta \cdot x} \right)+\left( {1-\frac{1}{\beta \cdot d}} \right)\cdot \sin \left( {\beta \cdot x} \right)} \right)} \right); \] \[ M_{x} =\frac{\gamma \cdot a\cdot d\cdot h}{\sqrt {12\cdot \left( {1-\nu ^{2}} \right)} }\cdot e^{-\beta \cdot x}\cdot \left( {\sin \left( {\beta \cdot x} \right)-\left( {1-\frac{1}{\beta \cdot d}} \right)\cdot \cos \left( {\beta \cdot x} \right)} \right); \] \[ M_{\phi } =\nu \cdot M_{x} =\frac{\gamma \cdot a\cdot d\cdot h\cdot \nu }{\sqrt {12\cdot \left( {1-\nu^{2}} \right)} }\cdot e^{-\beta \cdot x}\cdot \left( {\sin \left( {\beta \cdot x} \right)-\left( {1-\frac{1}{\beta \cdot d}} \right)\cdot \cos \left( {\beta \cdot x} \right)} \right); \] \[ N_{x} =0; \quad N_{\phi } =\frac{E\cdot h}{a}\cdot w=\gamma \cdot a\cdot d\cdot \left( {1-\frac{x}{d}-e^{-\beta \cdot x}\cdot \left( {\cos \left( {\beta \cdot x} \right)+\left( {1-\frac{1}{\beta \cdot d}} \right)\cdot \sin \left( {\beta \cdot x} \right)} \right)} \right),\quad где: \]\[ \beta =\sqrt[4]{\frac{3\cdot \left( {1-\nu^{2}} \right)}{a^{2}\cdot h^{2}}}. \]
