Толстая квадратная в плане плита, шарнирно опертая по боковым граням, под действием поперечной нагрузки, распределенной по верхней грани по закону косинуса
Цель: Определение напряженно-деформированного состояния толстой квадратной в плане плиты, шарнирно опертой по боковым граням, от действия поперечной нагрузки, распределенной по верхней грани по закону косинуса в соответствии с объемной задачей теории упругости.
Использованная версия SCAD: 21.1
Файлы с исходными данными:
| Имя файла | Описание файла расчета |
|---|---|
| 4.36a_gamma_3.SPR | Расчетная схема для толщины плиты 4 м (γ = a / h = 3) |
Формулировка задачи: Толстая квадратная в плане плита шарнирно оперта по боковым граням и находится под воздействием поперечной нагрузки, распределенной по верхней грани по закону косинуса q·cos((π·x)/(2∙a))∙cos((π·y)/(2∙a)).
Определить:
- распределение горизонтальных нормальных напряжений σx по толщине плиты z в ее центре
(x = 0, y = 0); - распределение горизонтальных касательных напряжений τxy по толщине плиты z на ее боковом ребре
(x = a, y = a);
- значение вертикальных нормальных напряжений σz в центре плиты
(x = 0, y = 0, z = 0); - значение вертикальных касательных напряжений τxz на середине боковой грани плиты
(x = a, y = 0, z = 0); - распределение вертикальных перемещений z по толщине плиты z в ее центре
(x = 0, y = 0); - распределение горизонтальных перемещений x по толщине плиты на середине ее боковой грани
(x = a, y = 0, z = 0).
Ссылки: М.К. Усаров, Задача изгиба для толстой ортотропной пластины в трехмерной постановке, Magazine of Civil Engineering, 2011, № 4, стр. 40-47.
Исходные данные:
| E = 1.0·105 тс/м102 | - модуль упругости материала плиты; |
| υ = 0.3 | - коэффициент Пуассона материала плиты; |
| 2∙a = 30.0 м | - длина стороны плиты; |
| 2∙h = 10.0 м | - толщина плиты; |
| q = 10.0 тс/м2 | - амплитудное значение поперечной нагрузки, распределенной по верхней грани плиты по закону косинуса. |
Конечноэлементная модель: Расчетная схема – система общего вида, элементы плиты – 72000 объемных восьмиузловых изопараметрических элементов типа 36. Сетка конечных элементов плиты в плане и по толщине имеет шаг 0.5 м. Направление выдачи внутренних усилий сориентировано по осям общей системы координат. По узлам боковых граней плиты x = ± a установлены связи по линейным степеням свободы Y, Z; По узлам боковых граней плиты y = ± a установлены связи по линейным степеням свободы X, Z. Количество узлов в расчетной схеме – 78141.
Результаты решения в SCAD
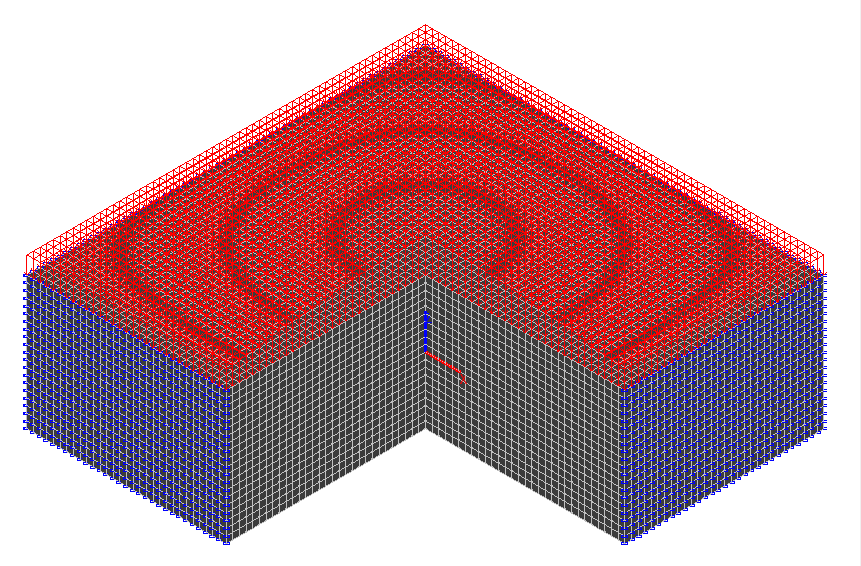
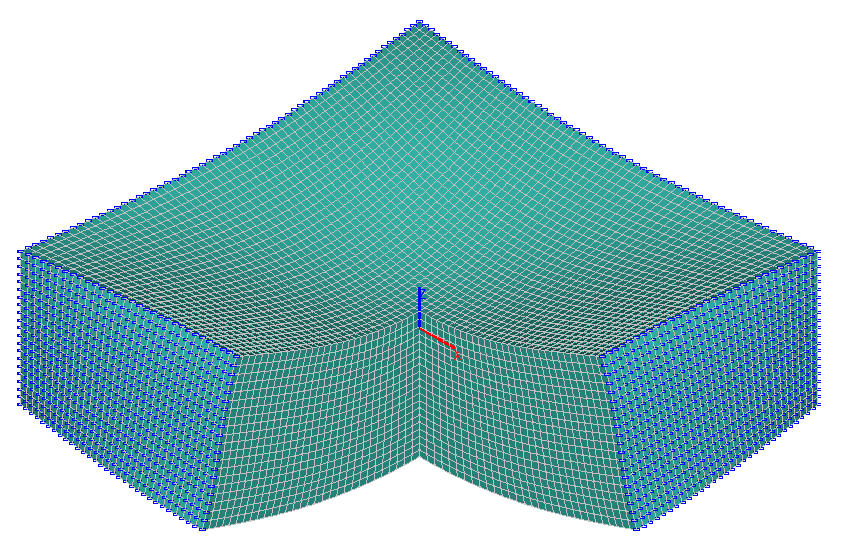
Расчетная и деформированная схемы
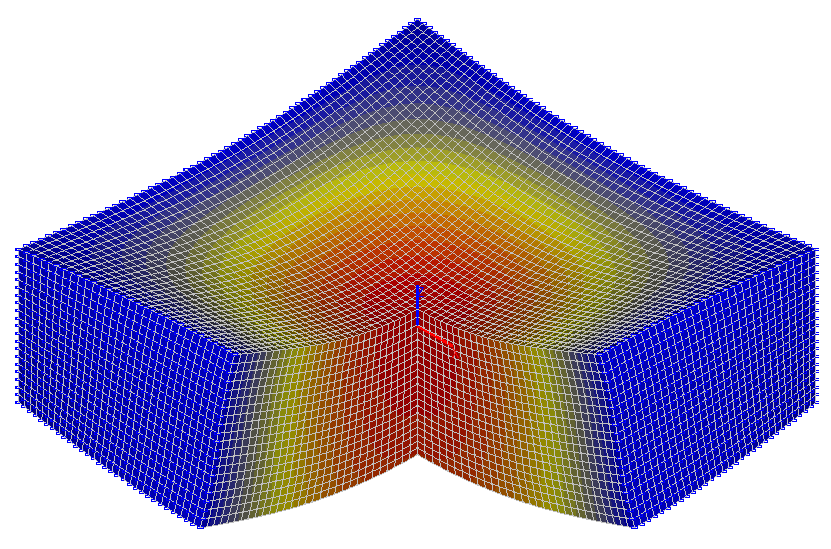

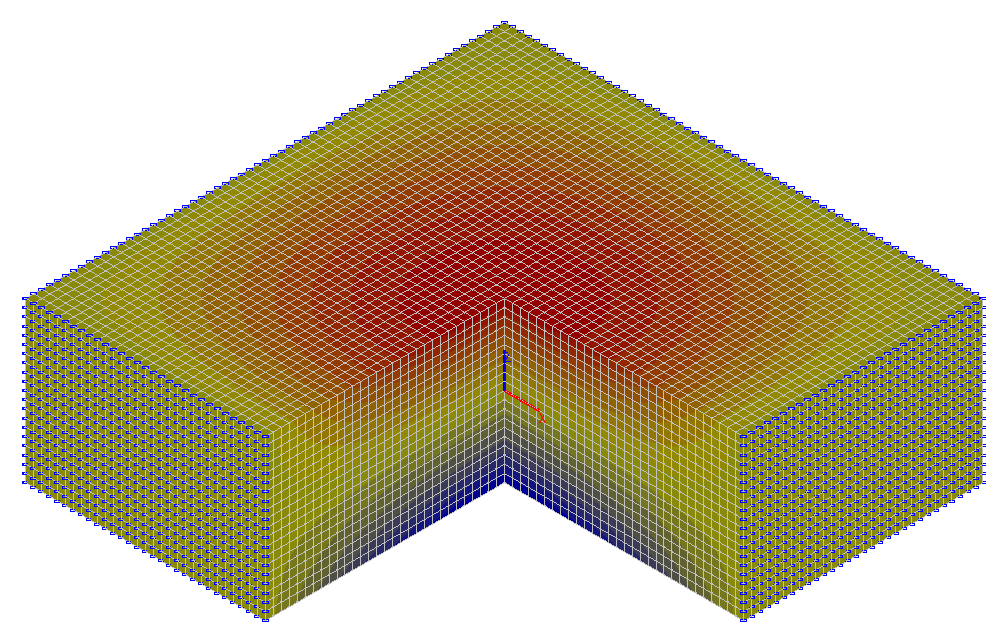
Значения вертикальных перемещений z (мм)
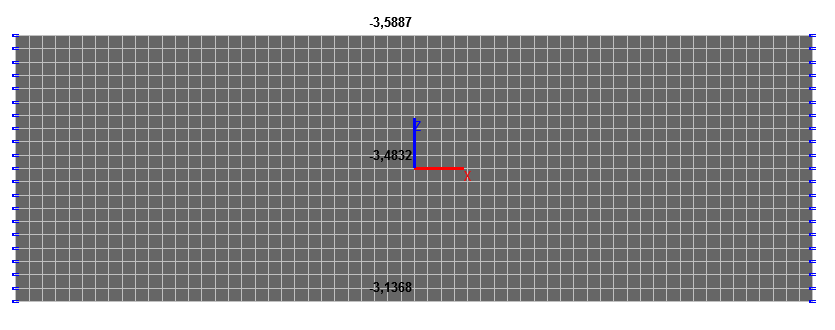
Значения вертикальных перемещений z (мм) в центре плиты (x = 0, y = 0)
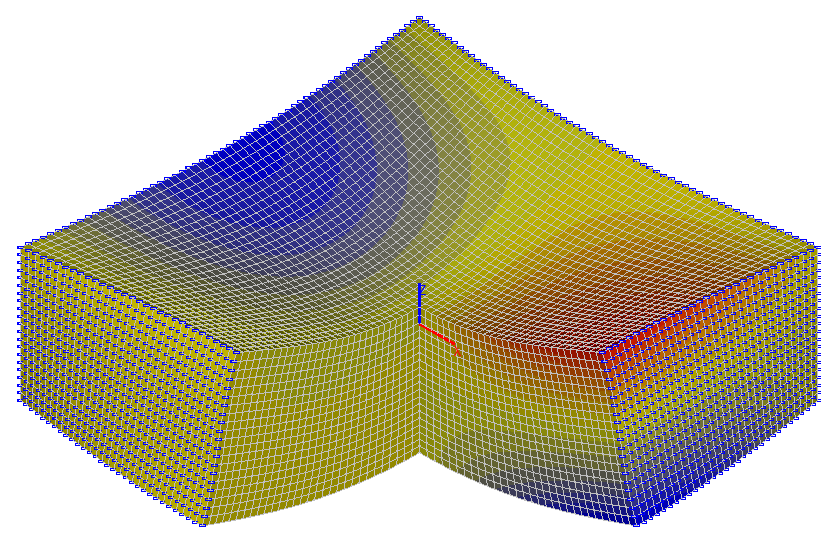
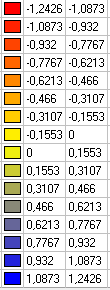
Значения горизонтальных перемещений x (мм)
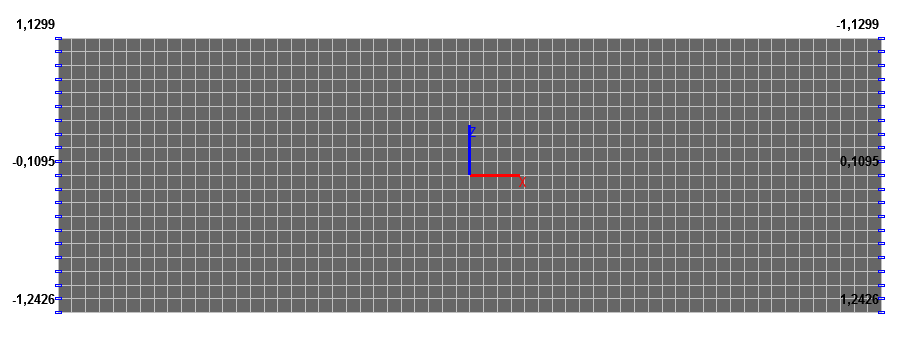
Значения горизонтальных перемещений x (мм) на середине боковых граней плиты (x = ± a, y = 0, z = 0)
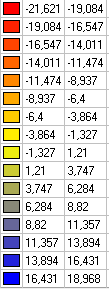
Значения горизонтальных нормальных напряжений σx (тс/м2)
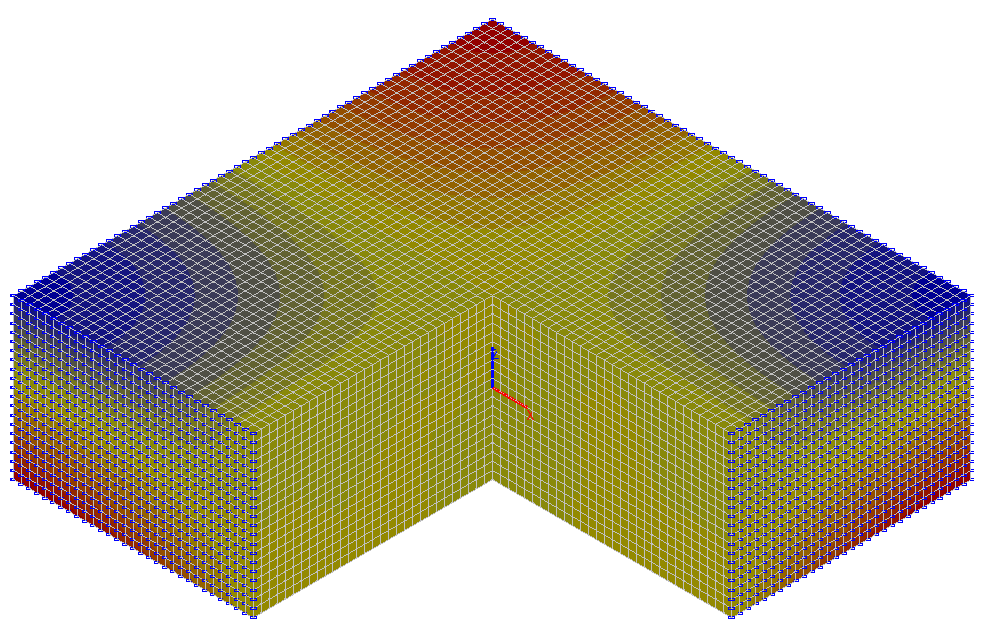

Значения горизонтальных касательных напряжений τxy (тс/м2)
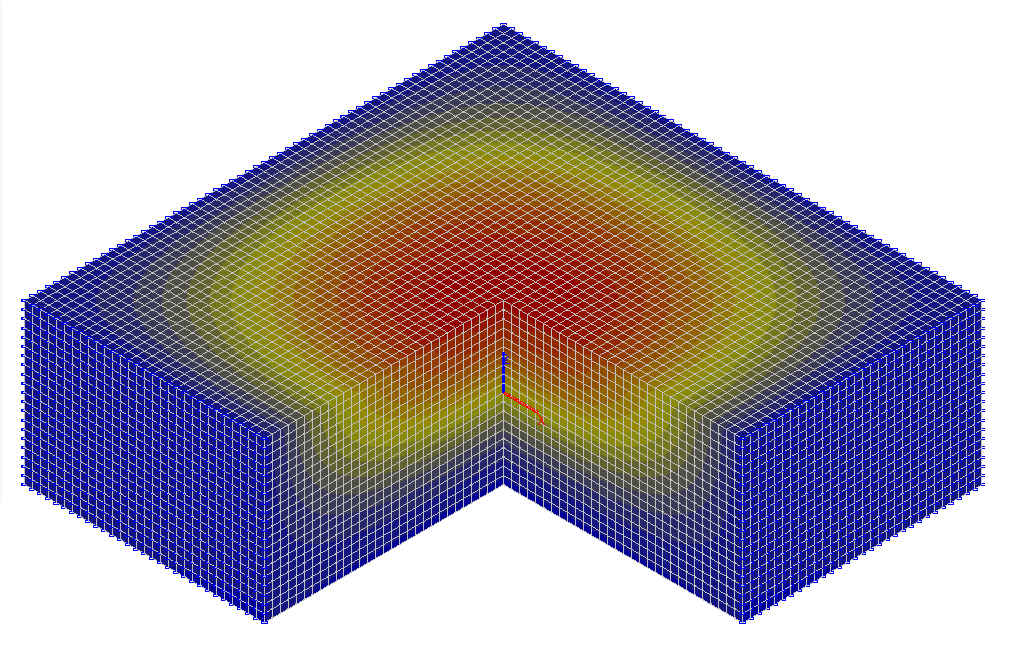

Значения вертикальных нормальных напряжений σz (тс/м2)
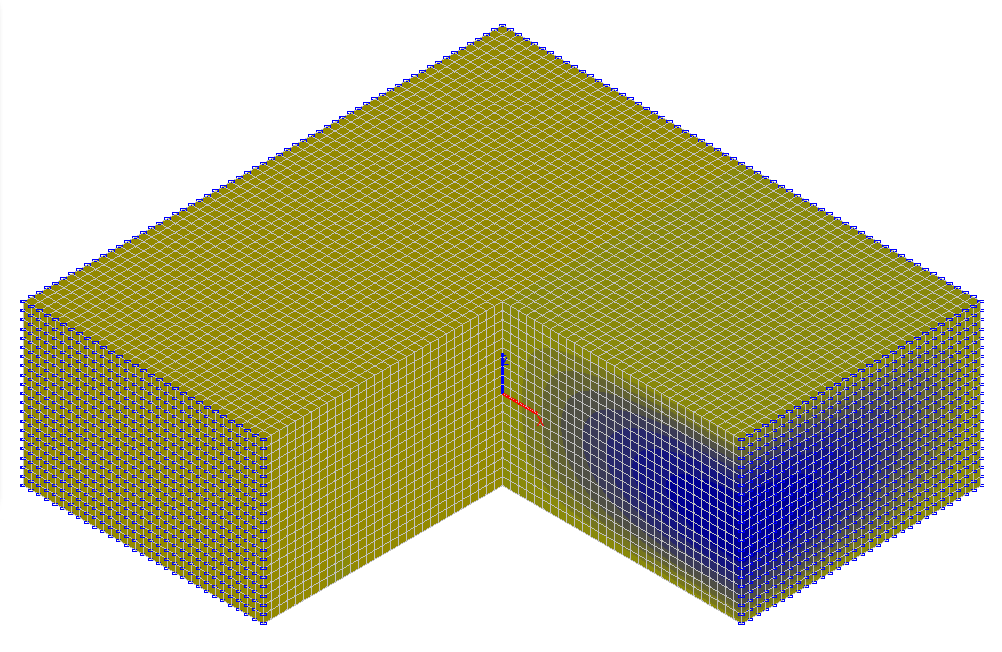

Значения вертикальных касательных напряжений τxz (тс/м2)
Сравнение решений:
|
z / h |
σx , тс/м2 (x = y = 0) |
τxy , тс/м2 (x = y = a) |
||||
|---|---|---|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
Теория |
SCAD |
Отклонения, % |
|
|
1.0 |
-21.240 |
-21.591 |
1.65 |
9.129 |
9.098 |
0.34 |
|
0.0 |
-0.481 |
-0.479 |
0.42 |
-0.882 |
-0.881 |
0.11 |
|
-1.0 |
18.639 |
18.942 |
1.63 |
-10.036 |
-10.005 |
0.31 |
|
z / h |
σz , тс/м2 (x = y = 0) |
τxz , тс/м2 (x = a, y = 0) |
||||
|---|---|---|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
Теория |
SCAD |
Отклонения, % |
|
|
0.0 |
-4.944 |
-4.939 |
0.10 |
7.023 |
6.996 |
0.38 |
|
z / h |
z, мм (x = y = 0) |
x, мм (x = a, y = 0) |
||||
|---|---|---|---|---|---|---|
|
Теория |
SCAD |
Отклонения, % |
Теория |
SCAD |
Отклонения, % |
|
|
1.0 |
-3.5963 |
-3.5887 |
0.21 |
-1.1333 |
-1.1299 |
0.30 |
|
0.0 |
-3.4906 |
-3.4832 |
0.21 |
0.1095 |
0.1095 |
0.00 |
|
-1.0 |
-3.1440 |
-3.1368 |
0.23 |
1.2459 |
1.2426 |
0.26 |
Замечания: При аналитическом решении горизонтальные нормальные напряжения σx по толщине плиты z в ее центре (x = 0, y = 0), горизонтальные касательные напряжения τxy по толщине плиты z на ее боковом ребре (x = a, y = a), вертикальные нормальные напряжения σz в центре плиты (x = 0, y = 0, z = 0), вертикальные касательные напряжения τxz на середине боковой грани плиты (x = a, y = 0, z = 0), вертикальные перемещения z по толщине плиты z в ее центре (x = 0, y = 0), горизонтальные перемещения x по толщине плиты на середине ее боковой грани (x = a, y = 0, z = 0) для υ = 0.3 и γ = a / h = 3 могут быть вычислены по следующим формулам:
\[ \frac{z}{h}=1.0: \quad \sigma_{x} =-2.1240\cdot q; \quad \tau_{xy} =-0.9129\cdot q; \quad \\ z=-3596.3\cdot \frac{q\cdot 2\cdot h}{E}; \quad x=-1133.3\cdot \frac{q\cdot 2\cdot h}{E}; \] \[ \frac{z}{h}=0.0: \quad \sigma_{x} =-0.0481\cdot q; \quad \tau_{xy} =-0.0882\cdot q \quad \sigma_{z} =-0.4944\cdot q; \quad \\ \tau_{xy} =0.7023\cdot q \quad z=-3490.6\cdot \frac{q\cdot 2\cdot h}{E}; \quad x=109.5\cdot \frac{q\cdot 2\cdot h}{E}; \] \[ \frac{z}{h}=-1.0: \quad \sigma_{x} =1.8639\cdot q; \quad \tau_{xy} =1.0036\cdot q; \quad z=-3144.0\cdot \frac{q\cdot 2\cdot h}{E}; \quad x=1245.9\cdot \frac{q\cdot 2\cdot h}{E}; \]
