Толстая круглая в плане плита, жестко защемленная по боковой поверхности, под действием равномерно распределенной по верхнему основанию нагрузки
Цель: Определение напряженно-деформированного состояния толстой круглой в плане плиты, жестко защемленной по боковой поверхности, от действия равномерно распределенной по верхнему основанию нагрузки в соответствии с объемной задачей теории упругости.
Использованная версия SCAD: 21.1
Файлы с исходными данными:
|
Имя файла |
Описание файла расчета |
|---|---|
|
Расчетная схема для толщины плиты 4 м |
|
|
Расчетная схема для толщины плиты 6 м |
Формулировка задачи: Толстая круглая в плане плита жестко защемлена по боковой поверхности и находится под воздействием равномерно распределенной по верхнему основанию нагрузки q. Определить:
- распределение радиальных σr и вертикальных σz нормальных напряжений по толщине плиты в ее центре (r = 0);
- распределение вертикальных перемещений w по толщине плиты в ее центре (r = 0).
Ссылки: Соляник-Красса К.В. Осесимметричная задача теории упругости. – М.: Стройиздат. 1987. 336с.
Исходные данные:
| E = 1.0·107 кПа | - модуль упругости; |
| μ = 0.25 | - коэффициент Пуассона; |
| 2∙a = 20.0 м | - диаметр плиты; |
| 2∙h = 4.0 м; 6.0 м | - толщина плиты; |
| q = 10 кПа | - равномерно распределенная по верхней грани нагрузка. |
Конечноэлементная модель
Сетка конечных элементов разбита по радиусу с шагом 0.5 м и по толщине на 16-ть слоев (схемы 1х1).
Элементы расчетной схемы:
- 4384 объемных 20-ти узловых изопараметрических элементов типа 37 (параллелепипед);
- 400 объемных 15-ти узловых элементов изопараметрических элементов типа 35(треугольная призма).
Узлов расчетной схемы – 20866.
Расчет выполнен с учетом плоскостей симметрии. Заданы связи:
- на боковой поверхности по всем линейным степенями свободы;
- на плоскости YOZ – по x;
- на плоскости XOZ – по y.
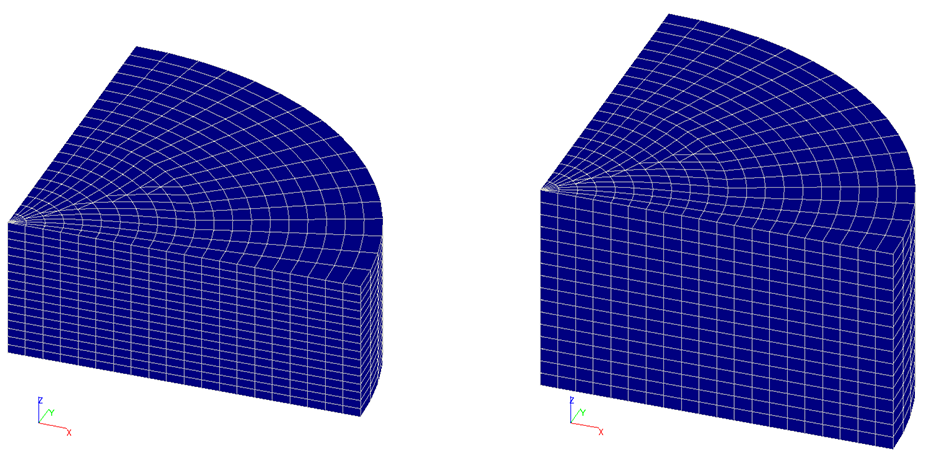
Расчетные схемы плит толщиной 4.0 м и 6.0 м
Результаты решения в SCAD
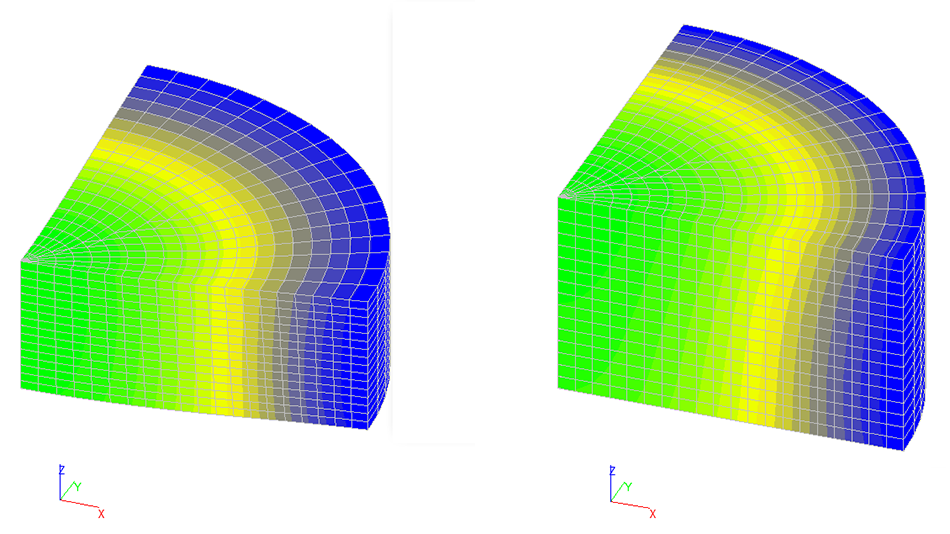
Значения вертикальных перемещений w (мм) в плитах толщиной 4.0 м 6.0 м
Сравнение решений:
|
Толщина |
Вели-чина |
Точка |
Прибли-женная |
SCAD |
Отклонение (%) |
|---|---|---|---|---|---|
|
4m |
w(mm) |
(0,0,2) |
-0.0436 |
–0.04538 |
4.08 |
|
(0,0,0) |
–0.0424 |
–0.0454 |
7.08 |
||
|
(0,0,–2) |
–0.0411 |
–0.04364 |
6.18 |
||
|
σr=σθ (кПа) |
(0,0,2) |
-34.51 |
-33.78 |
2.12 |
|
|
(0,0,0) |
-1.6667 |
-1.5547 |
6.72 |
||
|
(0,0,-2) |
31.1719 |
30.62 |
1.76 |
||
|
σz (кПа) |
(0,0,2) |
-10 |
-10.16 |
0.16 |
|
|
(0,0,0) |
-5 |
-5.07 |
0.14 |
||
|
(0,0,-2) |
0 |
-0.05 |
– |
||
|
6m |
w |
(0,0,3) |
-0.02097 |
-0.02112 |
0.72 |
|
(0,0,0) |
-0.01916 |
-0.01994 |
4.07 |
||
|
(0,0,-3) |
-0.01722 |
-0.01851 |
7.49 |
||
|
σr=σθ (кПа) |
(0,0,3) |
-18.2292 |
-18.51 |
1.54 |
|
|
(0,0,0) |
-1.6667 |
-1.5149 |
9.12 |
||
|
(0,0,-3) |
14.896 |
14.4884 |
2.74 |
||
|
σz (кПа) |
(0,0,3) |
-10 |
-9.797 |
2.03 |
|
|
(0,0,0) |
-5 |
-5.0569 |
1.14 |
||
|
(0,0,-3) |
0 |
0.043 |
– |
Замечание 1: Приближенные аналитические значения вычислены по формулам, приведенным на стр. 124-125 в книге «Соляник-Красса К.В. Осесимметричная задача теории упругости. – М.: Стройиздат. 1987.»
Замечания 2: Были выполнены расчеты с уменьшением шага сетки в два и четыре раза (схемы 4х4) для исследования сходимости метода. Расчеты также выполнены с учетом плоскостей симметрии. Максимальная расчетная схема содержала:
- 280576 объемных 20-ти узловых изопараметрических элементов типа 37 (параллелепипед);
- 25600 объемных 15-ти узловых элементов изопараметрических элементов типа 35 (треугольная призма).
Узлов расчетной схемы – 1222501.
Сравнение решений SCAD:
|
Толщина |
Вели-чина |
Точка |
SCAD |
Отклонение (%) |
|
|---|---|---|---|---|---|
|
4х4 |
1х1 |
||||
|
4m |
w(mm) |
(0,0,2) |
-0.04534 |
–0.04538 |
0.09 |
|
(0,0,0) |
-0.0454 |
–0.0454 |
– |
||
|
(0,0,–2) |
-0.04374 |
–0.04364 |
0.23 |
||
|
σr=σθ |
(0,0,2) |
-33.6603 |
-33.78 |
0.36 |
|
|
(0,0,0) |
-1.5683 |
-1.5547 |
0.87 |
||
|
(0,0,-2) |
30.527 |
30.62 |
0.30 |
||
|
σz |
(0,0,2) |
-10.0062 |
-10.16 |
1.36 |
|
|
(0,0,0) |
-5.0037 |
-5.0742 |
1.41 |
||
|
(0,0,-2) |
0.00326 |
-0.05 |
– |
||
|
6m |
w |
(0,0,3) |
-0.02108 |
-0.02112 |
0.19 |
|
(0,0,0) |
-0.01995 |
-0.01994 |
0.05 |
||
|
(0,0,-3) |
-0.01852 |
-0.01851 |
0.05 |
||
|
σr=σθ |
(0,0,3) |
-17.373 |
-17.557 |
1.06 |
|
|
(0,0,0) |
-1.5213 |
-1.5149 |
0.42 |
||
|
(0,0,-3) |
14.3485 |
14.4884 |
0.98 |
||
|
σz |
(0,0,3) |
-10.0006 |
-9.797 |
2.03 |
|
|
(0,0,0) |
-5.0367 |
-5.0694 |
0.65 |
||
|
(0,0,-3) |
0.0028 |
0.0434 |
– |
||
