Пространственная шарнирно-стержневая система под действием сосредоточенной силы
Цель: Определение напряженного состояния в элементах пространственной шарнирно-стержневой системы от воздействия сосредоточенной силы.
Файл с исходными данными: CS01_v11.3.spr
Формулировка задачи: Три стержня пространственной системы шарнирно сопряжены в общем узле (4) и шарнирно оперты в противоположных узлах (1, 2, 3). Опорные узлы расположены в одной горизонтальной плоскости, общий узел лежит вне этой плоскости и нагружен вертикальной сосредоточенной силой P. Определить продольные усилия N в каждом стержне.
Ссылки: F. P. Beer, E. R. Johnston Jr., D. F. Mazurek, P. J. Cornwell, E. R. Eisenberg, Vector Mechanics for Engineers, Statics and Dynamics, New York, McGraw-Hill Co., 1962, p. 47.
Исходные данные:
| E = 3.0·107 Па | - модуль упругости, |
| A = 1.0 м2 | - площадь поперечного сечения стержней; |
| P = 50 Н | - значение сосредоточенной силы. |
Конечноэлементная модель: Расчетная схема - пространственная шарнирно-стержневая система, 3 стержневых элемента типа 4. Обеспечение граничных условий в опорных узлах достигается за счет наложения связей по направлениям степеней свободы: X, Y, Z. Количество узлов в расчетной схеме – 4.
Координаты узлов:
|
Узел |
X (м) |
Y (м) |
Z (м) |
|---|---|---|---|
|
1 |
0.0 |
0.0 |
0.0 |
|
2 |
0.0 |
72.0 |
0.0 |
|
3 |
96.0 |
0.0 |
0.0 |
|
4 |
48.0 |
24.0 |
-72.0 |
Результаты решения в SCAD
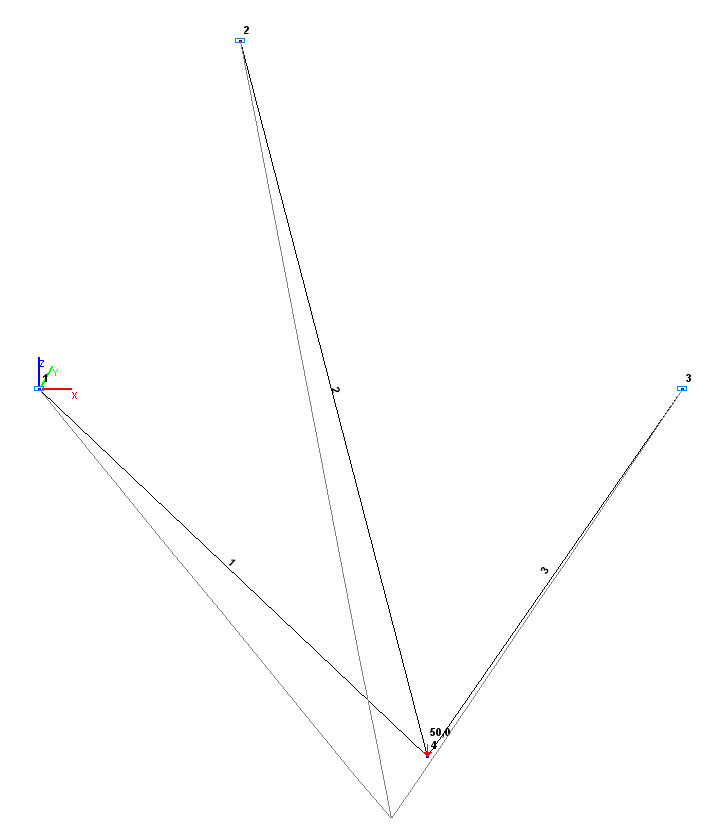
Расчетная и деформированная схемы
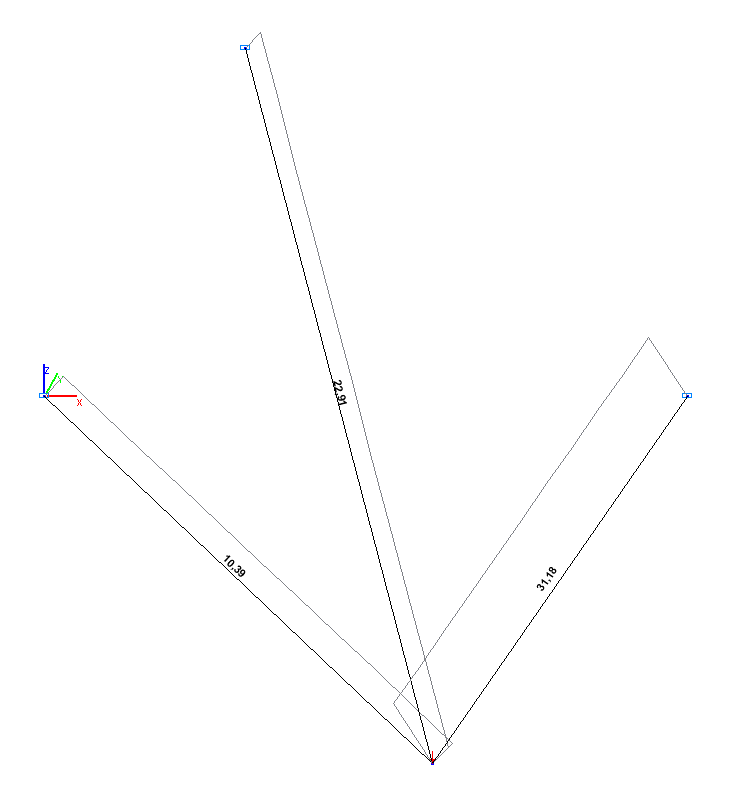
Эпюра продольных сил N (Н)
Сравнение решений:
Значения продольных сил N (Н)
|
Стержень (узлы) |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
1 (1-4) |
10.39 |
10.39 |
0.00 |
|
2 (2-4) |
22.91 |
22.91 |
0.00 |
|
3 (3-4) |
31.18 |
31.18 |
0.00 |
Замечания: При аналитическом решении продольные усилия N в элементах пространственной шарнирно-стержневой системы при вертикальной сосредоточенной нагрузке определяются по следующим формулам:
\[ N_{1} =-\frac{P\cdot \left( {x_{3} \cdot y_{2} -x_{3} \cdot y_{4} -x_{4} \cdot y_{2} } \right)\cdot \sqrt {x_{4}^{2}+y_{4}^{2}+z_{4}^{2}} }{x_{3} \cdot y_{2} \cdot z_{4} }; \] \[ N_{2} =-\frac{P\cdot y_{4} \cdot \sqrt {x_{4}^{2}+\left( {y_{2} -y_{4} } \right)^{2}+z_{4}^{2}} }{y_{2} \cdot z_{4} }; \] \[ N_{3} =-\frac{P\cdot x_{4} \cdot \sqrt {\left( {x_{3} -x_{4} } \right)^{2}+y_{4}^{2}+z_{4}^{2}} }{x_{3} \cdot z_{4} }. \]
