Цилиндрическое тело, свободное от закреплений, под действием продольной равномерно распределенной по торцам нагрузки
Цель: Определение деформированного состояния цилиндрического тела свободного от закреплений от воздействия продольной равномерно распределенной по торцам нагрузки.
Файл с исходными данными: SSLV01_v11.5.spr
Формулировка задачи: Цилиндрическое тело, свободное от закреплений, находится под воздействием продольной равномерно распределенной по торцам нагрузки F/A. Определить меридиональные ∆L и радиальные ∆R перемещения точек E, D, A (C) боковой поверхности цилиндра, отстоящих от поперечной плоскости его симметрии вдоль образующей соответственно на расстояния L/3, 2∙L/3, L, а также точки B центра его торцевой поверхности.
Ссылки: P. Germain, Introduction a la mecanique des milieux continus, Paris, Masson, 1986.
Исходные данные:
| E = 2.0·105 Па | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| R = 1.0 м | - радиус цилиндра; |
| L = 4.0 м | - длина цилиндра; |
| F/A = 1.0·102 Па | - равномерно распределенная по торцам нагрузка. |
Конечноэлементная модель: Расчетная схема – осесимметричная задача, осесимметричные элементы – 120 элементов оболочки типа 61. Сетка конечных элементов разбита с шагом 0.25 м в меридиональном направлении и с шагом 0.10 м в радиальном направлении. Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связей по условиям ее симметрии. Количество узлов в расчетной схеме – 143.
Результаты решения в SCAD
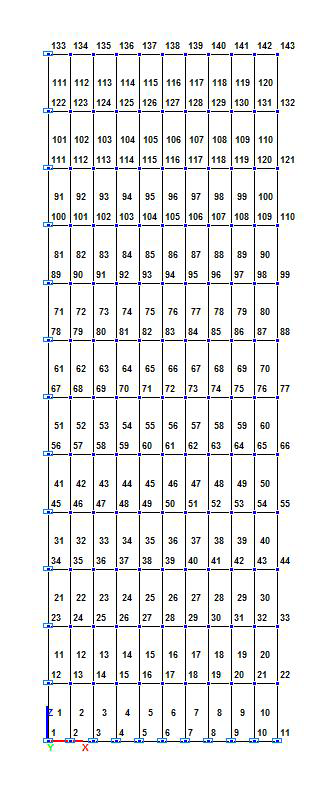
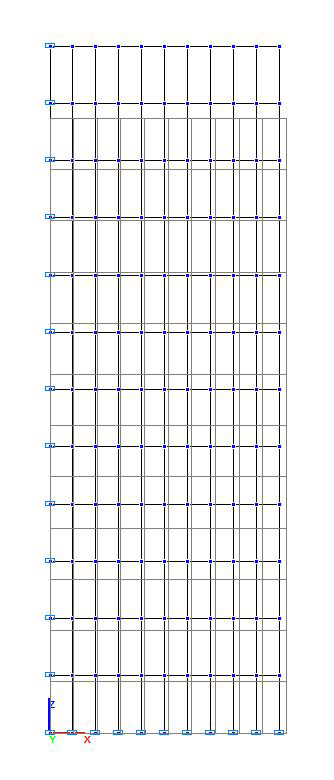
Расчетная и деформированная схемы
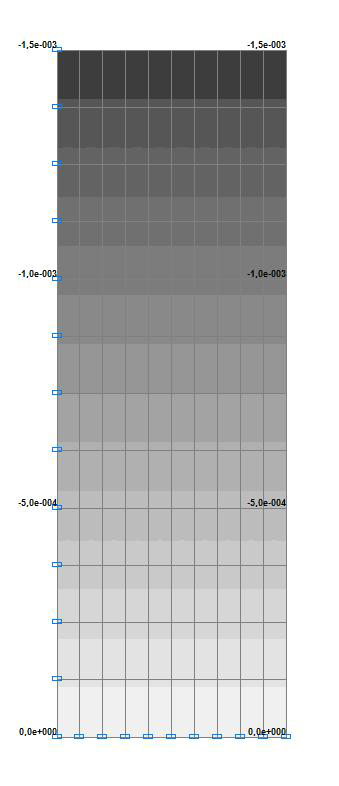
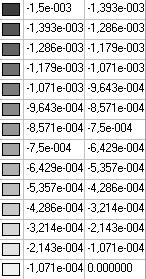
Значения меридиональных перемещений Z (∆L) м
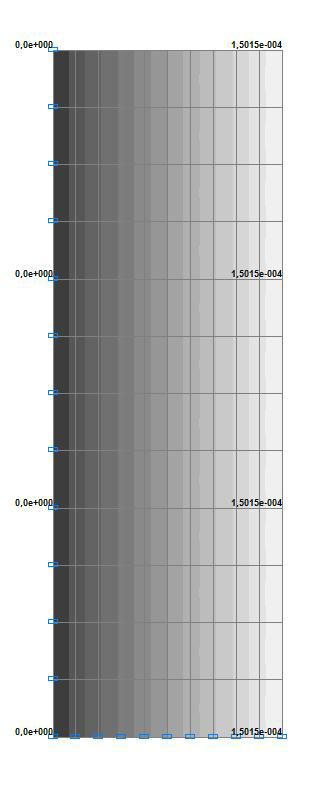
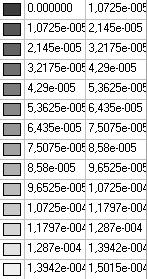
Значения радиальных перемещений X (∆R) м
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Меридиональное перемещение ∆L (точка E), м |
-0.500∙10-3 |
-0.500∙10-3 |
0.00 |
|
Радиальное перемещение ∆R (точка E), м |
-0.150∙10-3 |
-0.150∙10-3 |
0.00 |
|
Меридиональное перемещение ∆L (точка D), м |
-1.000∙10-3 |
-1.000∙10-3 |
0.00 |
|
Радиальное перемещение ∆R (точка D), м |
-0.150∙10-3 |
-0.150∙10-3 |
0.00 |
|
Меридиональное перемещение ∆L (точки A и C), м |
-1.500∙10-3 |
-1.500∙10-3 |
0.00 |
|
Радиальное перемещение ∆R (точки A и C), м |
-0.150∙10-3 |
-0.150∙10-3 |
0.00 |
|
Меридиональное перемещение ∆L (точка B), м |
-1.500∙10-3 |
-1.500∙10-3 |
0.00 |
|
Радиальное перемещение ∆R (точка B), м |
0.000∙10-3 |
0.000∙10-3 |
0.00 |
Замечания: При аналитическом решении меридиональные ∆L и радиальные ∆R перемещения могут быть вычислены по следующим формулам:
\[ \Delta L=\frac{P\cdot X}{E}; \quad \Delta R=\frac{\nu \cdot P\cdot R}{E}. \]
