Плоская ферма под действием мгновенных импульсов, сосредоточенных в неопорных узлах нижнего пояса

Цель: Определение деформированного состояния плоской фермы от воздействия мгновенных импульсов, сосредоточенных в неопорных узлах нижнего пояса.

Формулировка задачи: Плоская двухпролетная ферма с параллельными поясами и раскосной решеткой по три панели равной длины в каждом пролете опирается нижним поясом. В промежуточных (неопорных) узлах нижнего пояса сосредоточены массы M и действуют сосредоточенные мгновенные поперечные импульсы S. Определить собственные формы и частоты колебаний ω плоской фермы, а также поперечные перемещения узловых масс Z во времени.

Ссылки: И. М. Рабинович, А. П. Синицын, О.В. Лужин, В.М. Теренин, Расчет сооружений на импульсные воздействия, Москва, Стройиздат, 1970, стр. 153.

Исходные данные:

E = 2.0·108 тс/м2	- модуль упругости;
F = 1·10-2 м2	- площадь поперечного сечения элементов фермы, исключая стойку, находящуюся над средней опорой;
2· F = 2·10-2 м2	- площадь поперечного сечения стойки, находящейся над средней опорой;
a = 2.0 м	- высота фермы и длина панели фермы;
M = 16.0 тс·с2/м	- значение сосредоточенных масс в промежуточных (неопорных) узлах нижнего пояса фермы;
S = 4.0· тс·с	- значение сосредоточенных мгновенных поперечных импульсов, действующих в промежуточных (неопорных) узлах нижнего пояса фермы;
g = 10.00 м/с2	- значение ускорения свободного падения.

 

Конечноэлементная модель: По условиям симметрии конструкции и симметрии действия нагрузок рассматривается только половина фермы с раскреплением нижнего и верхнего пояса на оси симметрии в продольном (горизонтальном) направлении (степень свободы X) и уменьшением в два раза жесткости стойки, находящейся над средней опорой. Расчетная  схема – плоская шарнирно-стержневая система, 11 стержневых элементов типа 1. Обеспечение граничных условий по опорным узлам нижнего пояса фермы достигается за счет наложения связей по направлению степени свободы Z. Сосредоточенные массы задаются преобразованием статических узловых нагрузок M·g.

Расчет производится в два этапа: сначала модальным анализом определяются собственные формы и частоты колебаний ω, затем методом прямого интегрирования уравнений движения определяются поперечные перемещения узловых масс Z во времени. Воздействие сосредоточенных мгновенных поперечных импульсов описывается графиком изменения нагрузки во времени и задается в виде узловых сил, действующих по оси Z общей системы координат с масштабным множителем 1.0 и временем запаздывания 0.0 с. Интервалы между моментами времени графика изменения нагрузки равны Δt_int = 0.00001 c  и соответствуют шагу интегрирования. При построении графика импульсное воздействие принимается с прямоугольной функцией формы, значением силы P = 400000 тс и продолжительностью во времени  Δt_int = 0.00001 c. Продолжительность процесса во времени равна t = 0.12 с, что примерно соответствует величине удвоенного периода колебаний основного тона 4·π/ω₁. Коэффициенты критического демпфирования по 1-й и 2-й собственным частотам приняты с минимальным значением ξ = 0.0001. Коэффициент пересчета для присоединенного статического загружения равен k = 0.981 (формирование масс). Количество узлов в расчетной схеме – 7. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.

Результаты решения в SCAD

  
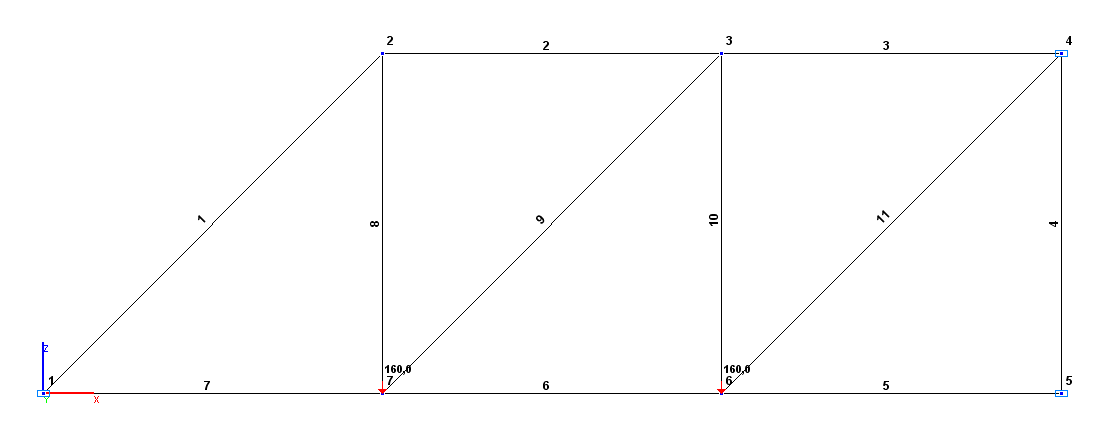
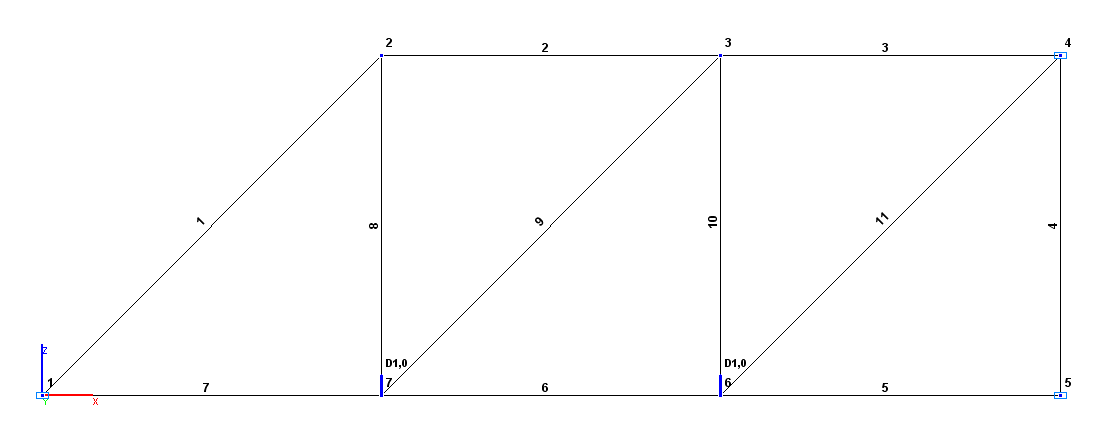
Расчетная схема

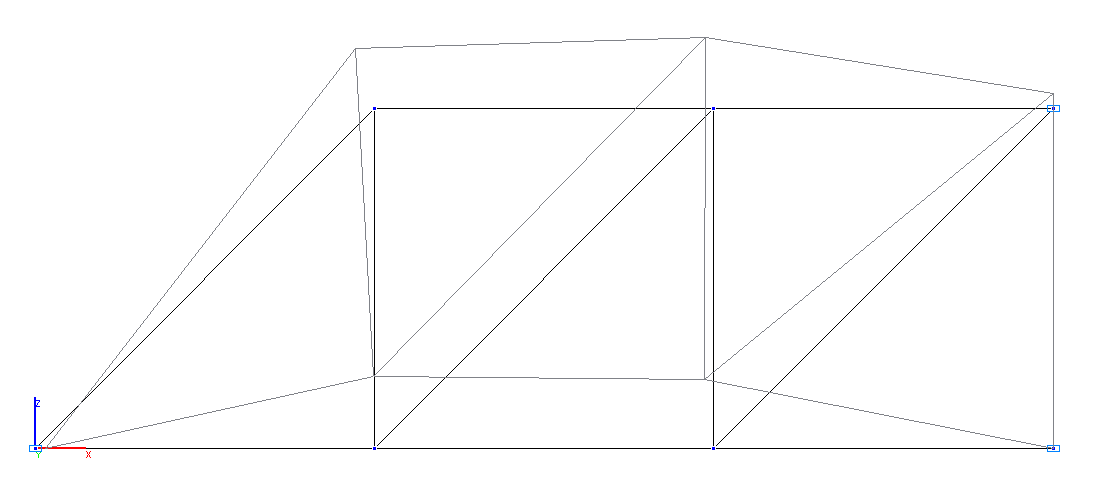
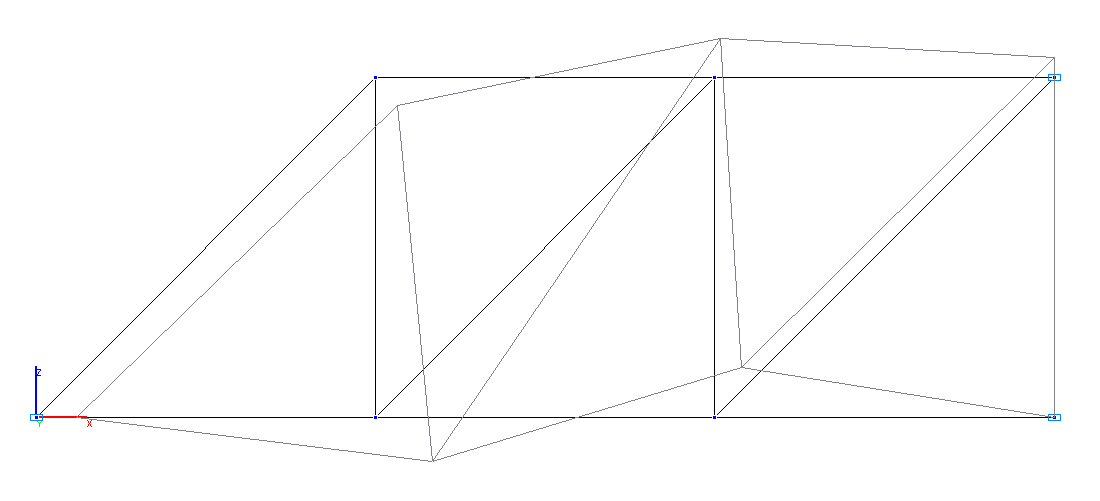
1-я и 2-я собственные формы колебаний (симметричные)

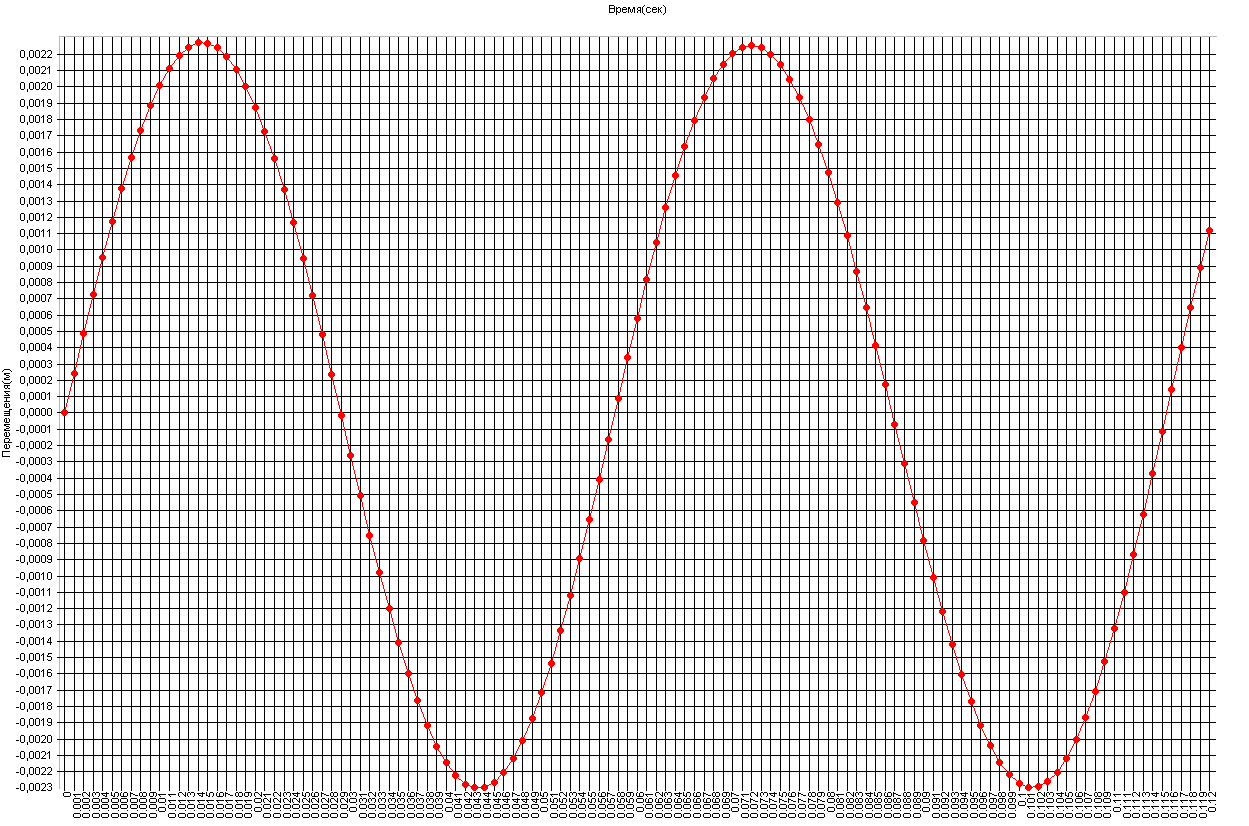
График изменения поперечных перемещений узловой массы Z7 (ближней к крайней опоре) во времени (м)

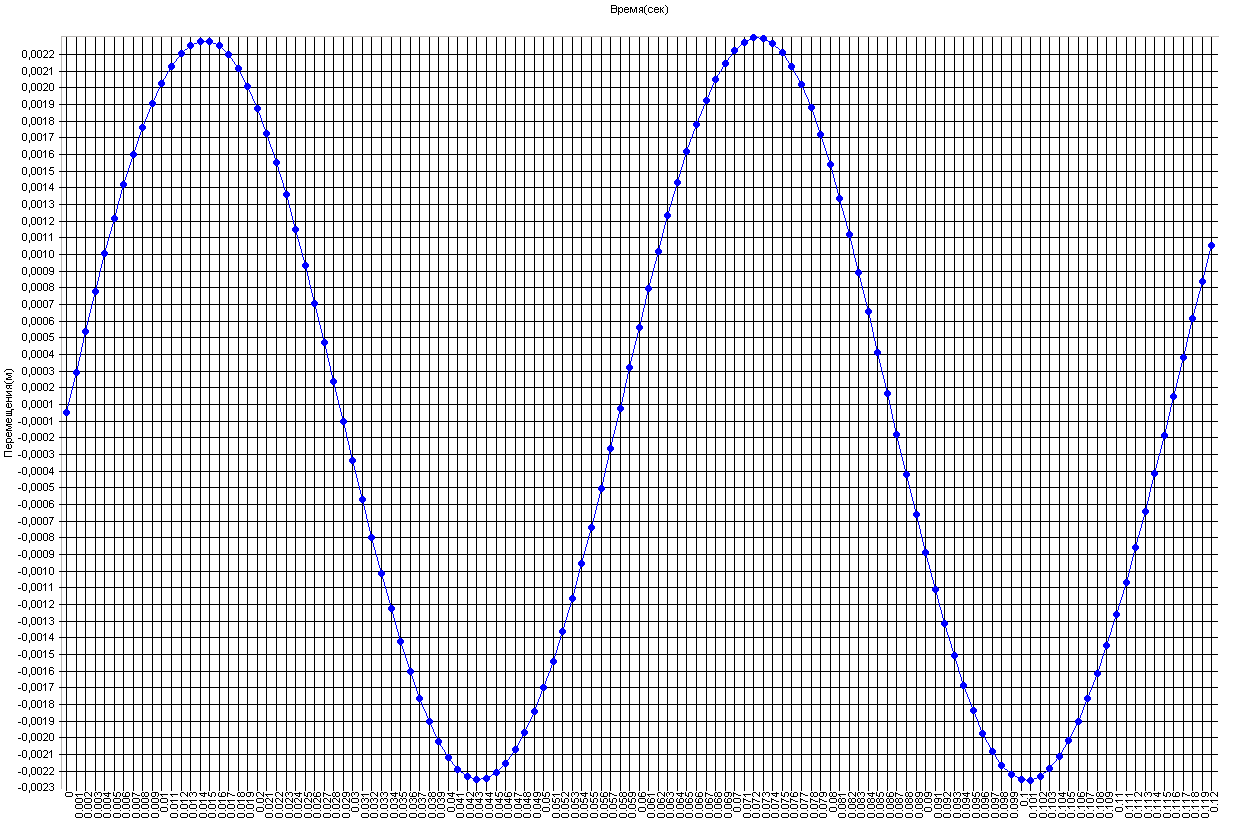
График изменения поперечных перемещений узловой массы Z6 (ближней к средней опоре) во времени (м)

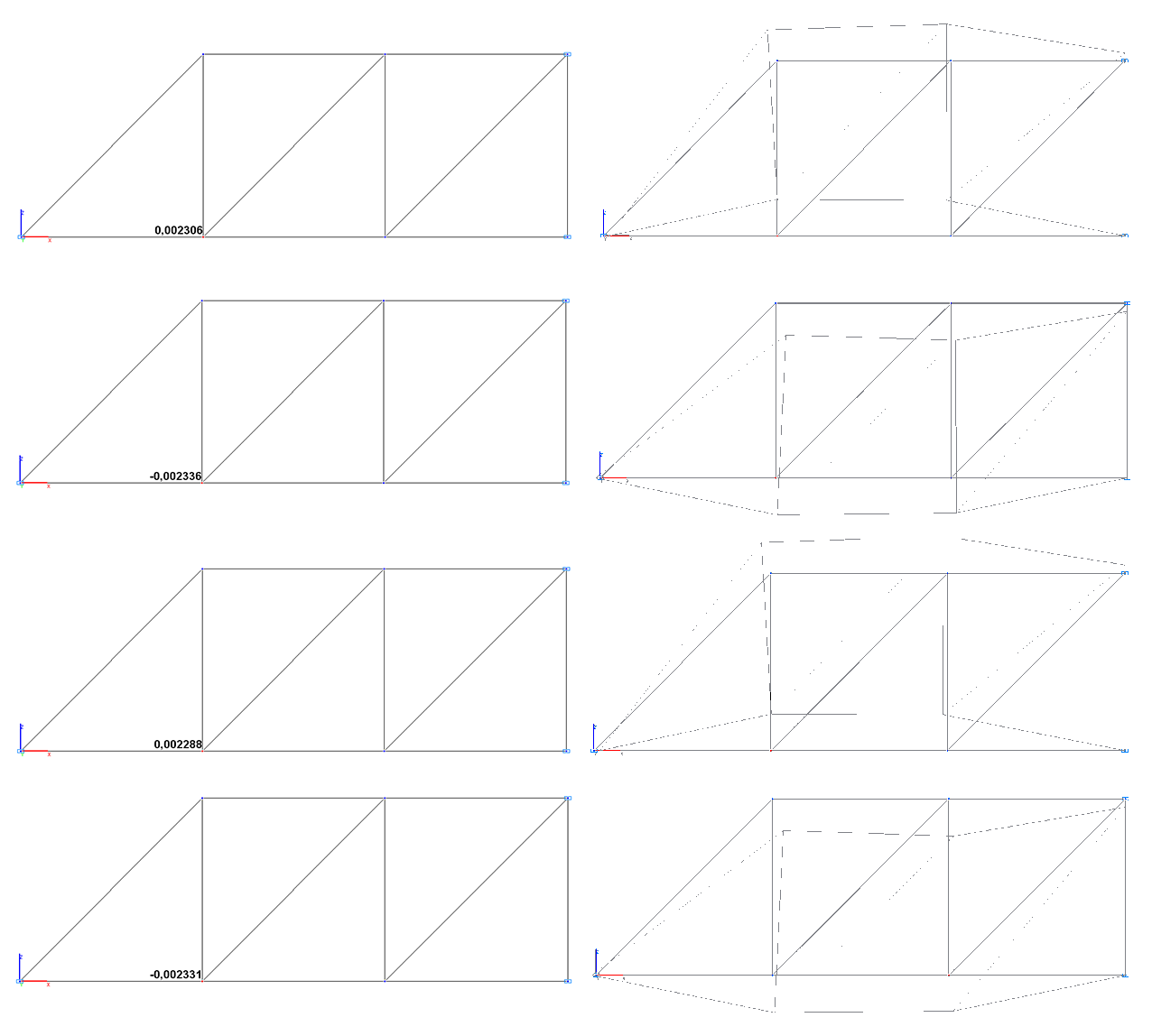
Амплитудные значения поперечных перемещений узловой массы Z7 (м) и деформированные схемы в соответствующие моменты

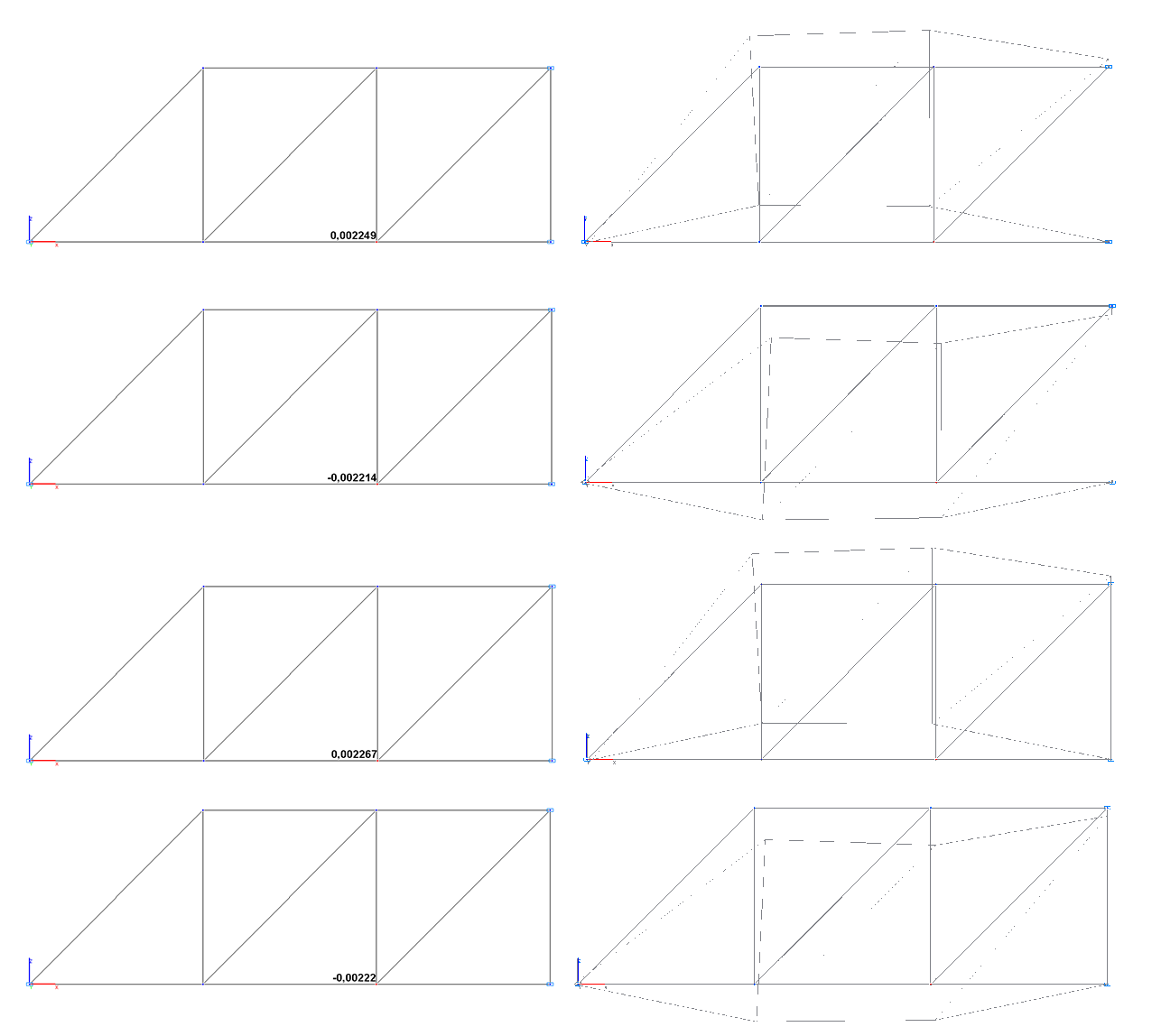
Амплитудные значения поперечных перемещений узловой массы Z6 (м) и деформированные схемы в соответствующие моменты

Сравнение решений:

Собственные частоты колебаний ω, рад/с

Форма колебаний	Теория	SCAD	Отклонения, %
1	112.0	108.8	2.86
2	208.0	197.4	5.10

Амплитудные значения поперечных перемещений узловых масс Z

Узловая масса	Теория		SCAD
	Время, с	Перемещение, м	Время, с	Перемещение, м	Отклонения, %
7	0.0142	0.002264	0.0144	0.002306	1.86
7	0.0420	-0.002280	0.0433	-0.002336	2.46
7	0.0702	0.002251	0.0720	0.002288	1.64
7	0.0982	-0.002287	0.1014	-0.002331	1.92
6	0.0139	0.002209	0.0145	0.002249	1.81
6	0.0422	-0.002192	0.0432	-0.002214	1.00
6	0.0701	0.002222	0.0724	0.002267	2.03
6	0.0982	-0.002185	0.1006	-0.002220	1.60

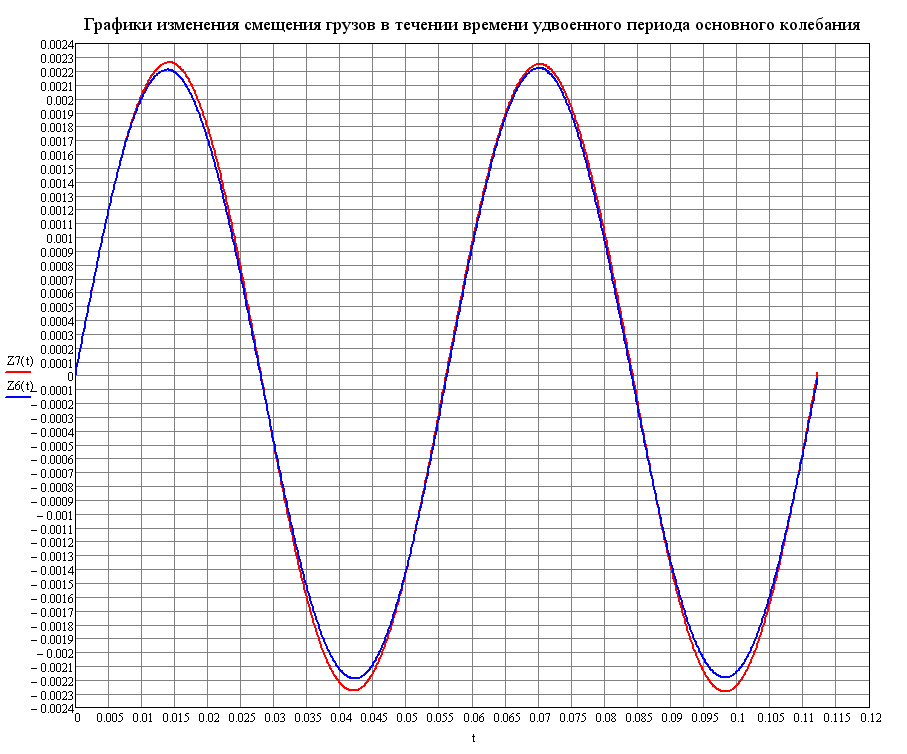
Графики изменения поперечных перемещений узловых масс Z7 и Z6 во времени по теоретическому решению (м)

Замечания: При выводе аналитического решения кроме учета симметрии были приняты следующие допущения:

• пренебрегается смещение масс в продольном (горизонтальном) направлении;
• пренебрегается разность взаимных поперечных (вертикальных) смещений нижних и верхних узлов каждой стойки фермы, ввиду чего массы сосредотачиваются только в нижних узлах;

При аналитическом решении собственные частоты колебаний ω плоской фермы определяются по формулам:

\[ \omega_{7} =0.448\cdot \sqrt {\frac{E\cdot F}{a\cdot M}} ; \quad \omega_{6} =0.832\cdot \sqrt {\frac{E\cdot F}{a\cdot M}} . \]

При аналитическом решении поперечные перемещения узловых масс плоской фермы Z во времени определяются по формулам:

\[ Z_{7} =1\cdot \frac{1.016\cdot S}{0.448\cdot M}\cdot \sqrt {\frac{a\cdot M}{E\cdot F}} \cdot \sin \left( {\omega_{1} \cdot t} \right)-1\cdot \frac{0.016\cdot S}{0.832\cdot M}\cdot \sqrt {\frac{a\cdot M}{E\cdot F}} \cdot \sin \left( {\omega_{2} \cdot t} \right); \] \[ Z_{6} =0.972\cdot \frac{1.016\cdot S}{0.448\cdot M}\cdot \sqrt {\frac{a\cdot M}{E\cdot F}} \cdot \sin \left( {\omega_{1} \cdot t} \right)+1.028\cdot \frac{0.016\cdot S}{0.832\cdot M}\cdot \sqrt {\frac{a\cdot M}{E\cdot F}} \cdot \sin \left( {\omega_{2} \cdot t} \right). \]

Расхождения с теорией для собственных частот колебаний связаны с тем, что в источнике "ручной" счет выполнен со значительными погрешностями.