Свободные колебания пространственного трубопровода, защемленного по торцам (задача Ховгарда)

Цель: Модальный анализ пространственного трубопровода, защемленного по торцам.

Файл с исходными данными: 5_1.spr

Формулировка задачи: Определить собственные формы и частоты колебаний f пространственного стального трубопровода, составленного из трех последовательно соединенных и взаимно ортогональных прямых участков, соединенных отводами, защемленного по торцам и заполненного водой.

Ссылки: William Hovgaard, Stresses in Three-dimensional Pipe Bends. Transactions of ASME, vol. 57, FSP 75-12, 1935.

Исходные данные:

E = 24.0·106 psi = 1.654740·108 кПа	- модуль упругости;
ν = 0.3	- коэффициент Пуассона;
De = 7.288 in = 0.185115 м	- наружный диаметр поперечного сечения трубы;
t = 0.241 in = 0.006121 м	- толщина поперечного сечения трубы;
ρs = 0.283 lb/in3 = 7.833 т/м3	- плотность материала трубы (сталь);
ρw = 0.036 lb/in3 = 0.996 т/м3	- плотность материала заполнения (вода);
Lstr1 = 108.9 in = 2.766 м	- длина первого прямого участка трубопровода;
Lstr2 = 35.6 in = 0.904 м	- длина второго прямого участка трубопровода;
Lstr3 = 41.0 in = 1.041 м	- длина третьего прямого участка трубопровода;
Relb = 36.3 in = 0.922 м	- радиус оси отводов трубопровода;

жесткостные характеристики и массы:

EA = E·(π·De2/4)·(1-(1-2·t/De)2) = 569598 Кн	- продольная жесткость поперечного сечения трубы;
EIb,str = E·(π·De4/64)·(1-(1-2·t/De)4) = 2283.81 Кн·м	- изгибная жесткость поперечного сечения прямого участка трубы;
EIb,elb = E·(π·De4/64)·(1-(1-2·t/De)4)/k = 995.824 Кн·м	- изгибная жесткость поперечного сечения отвода трубы (с учетом сплющивания),
где:
k = (10+12·λ2)/ (1+12·λ2) = 2.293391	- коэффициент гибкости по фон Карману,
λ = t·Relb/((De-2·t)/4) = 0.704654	- геометрический параметр;
GIt = (E/(2·(1+ ν)) ·(π·De4/32)·(1-(1-2·t/De)4) = 1756.78 Кн·м	- крутильная жесткость поперечного сечения трубы;
m = ·(π·De2/4)·(ρs -( ρs- ρw)(1-2·t/De)2)·g = 0.4938 кН/м	- погонная статическая нагрузка от веса трубы, заполненной водой.

 

Конечноэлементная модель: Расчетная  схема – система общего вида, элементы трубопровода – 38 стержневых элементов типа 5. Сетка конечных элементов разбита в продольном направлении (вдоль оси X1 местной системы координат) с шагом ≈ 0.2 м. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы X, Y, Z, UX, UY, UZ для торцевых узлов трубопровода. Распределенная масса задается преобразованием статической нагрузки от веса трубы, заполненной водой, m. Количество узлов в расчетной схеме – 39. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.

Результаты решения в SCAD

 
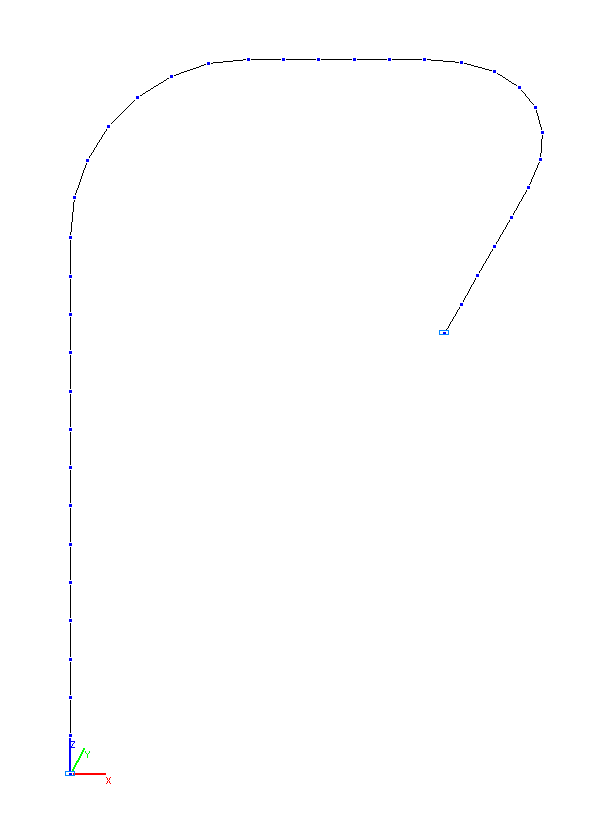
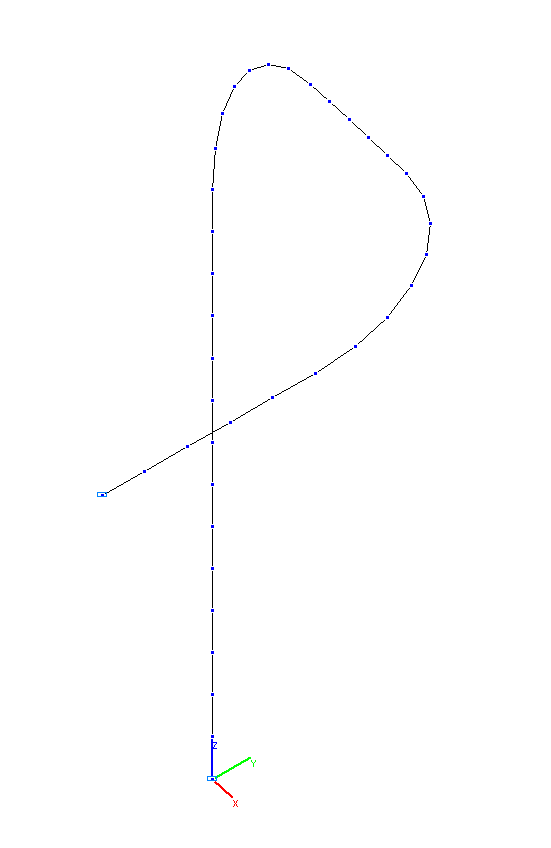
Расчетная схема

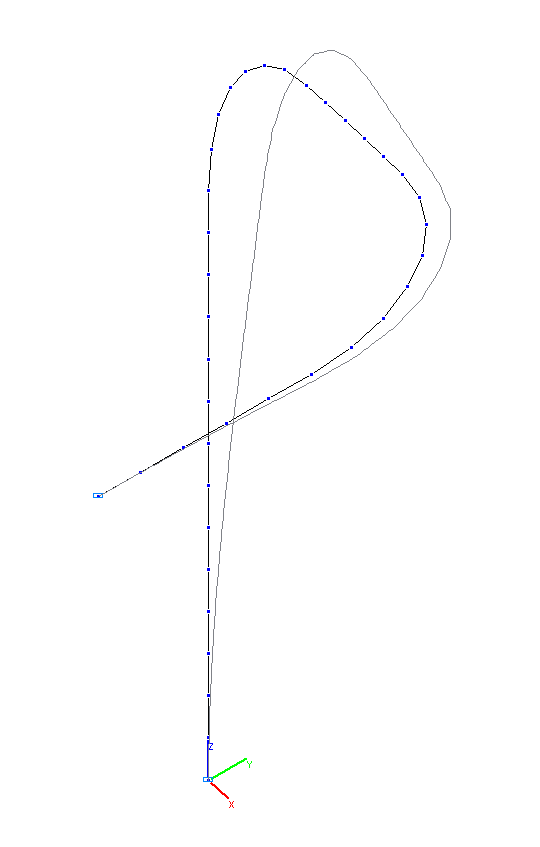
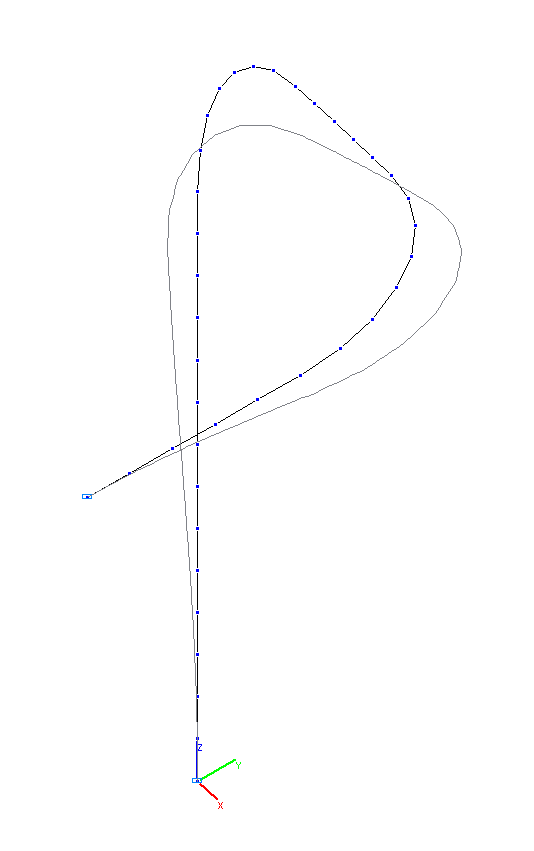
1-я и 2-я собственные формы колебаний

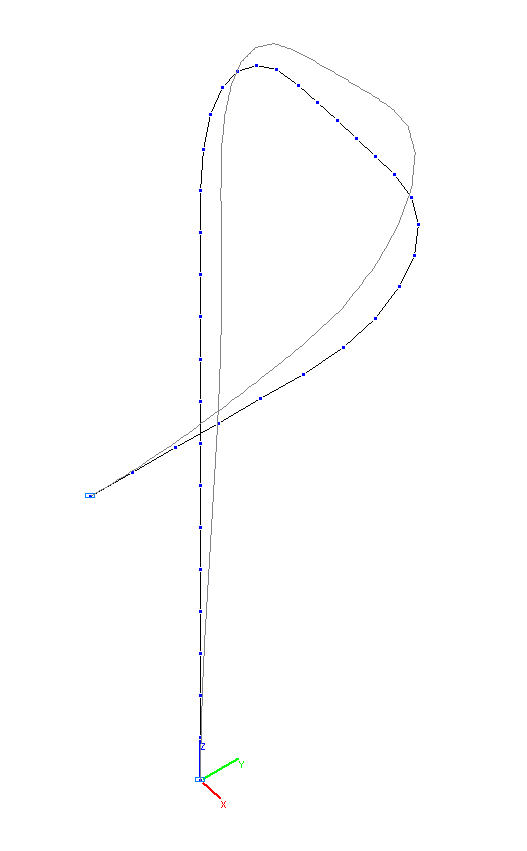
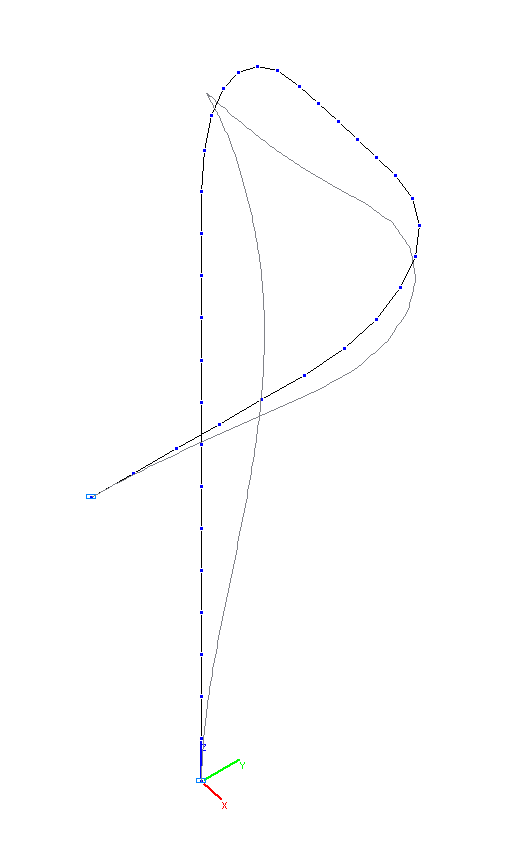
3-я и 4-я собственные формы колебаний

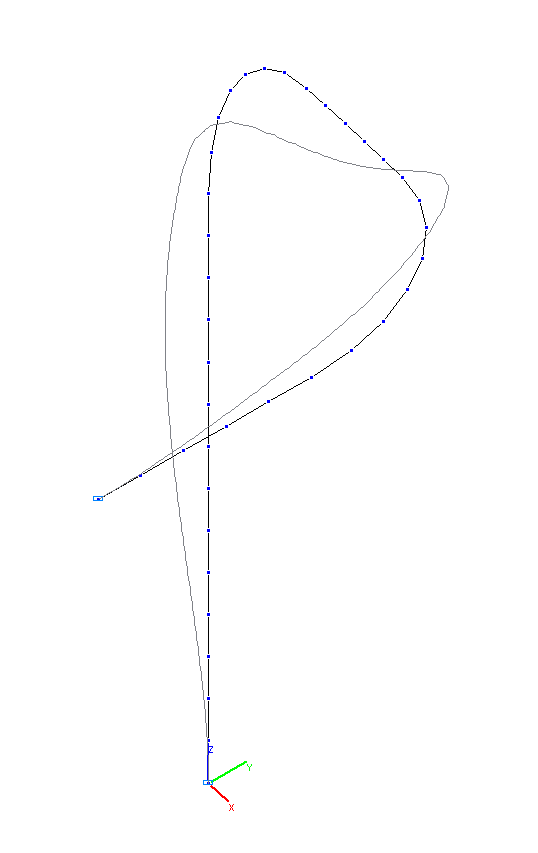
5-я и 6-я собственные формы колебаний

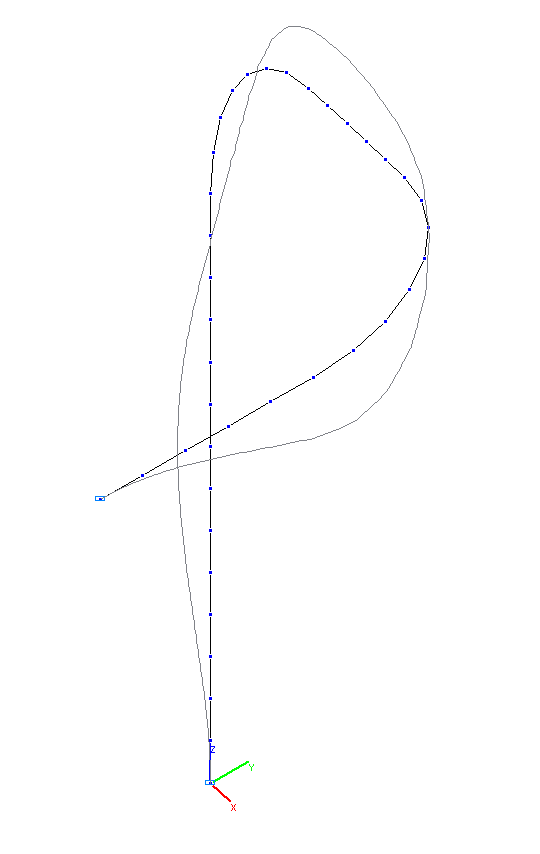
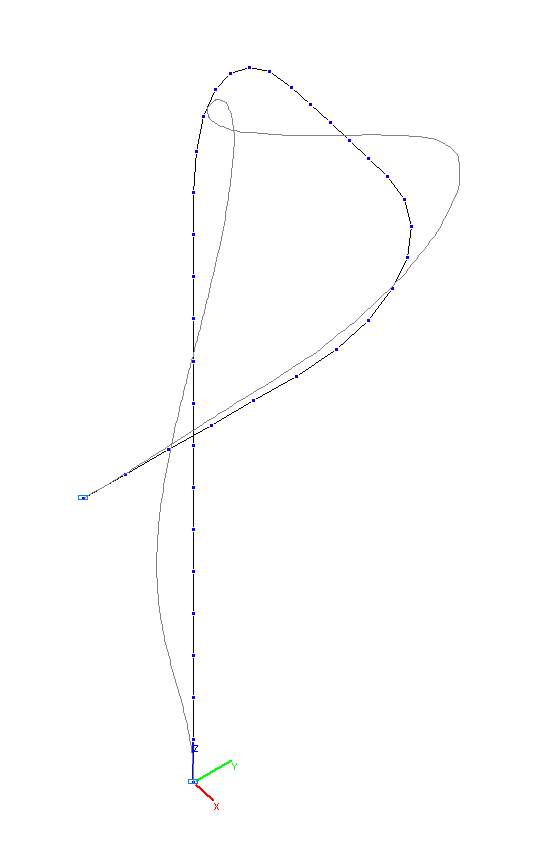
7-я и 8-я собственные формы колебаний

9-я собственные формы колебаний

Сравнение решений:

Собственные частоты колебаний f, Гц

Форма колебаний	Теория	SCAD	Отклонения, %
1	10.18	10.01	1.67
2	19.54	19.29	1.28
3	25.47	24.55	3.61
4	48.09	46.79	2.70
5	52.86	50.77	3.95
6	75.94	82.21	8.26
7	80.11	84.29	5.22
8	122.34	126.58	3.47
9	123.15	128.51	4.35