Свободно опертая невесомая балка с двумя сосредоточенными массами под действием на одну из них поперечной внезапно приложенной постоянной силы
Цель: Определение напряженно-деформированного состояния свободно опертой невесомой балки с двумя сосредоточенными массами от воздействия на одну из них поперечной внезапно приложенной постоянной силы.
Файлы с исходными данными:
5.12_Sudd_L.spr
График_5.12_Sudd_L.txt
Формулировка задачи: К свободно опертой балке постоянного сечения присоединены два одинаковых груза массой m на расстоянии четверти пролета от каждой из опор. Собственная масса балки по сравнению с массами грузов пренебрегается. В начальный момент времени к одной из масс прикладывается сила P, остающаяся в дальнейшем постоянной. Определить собственные формы и частоты колебаний p свободно опертой балки, а также прогибы η и изгибающие моменты M в поперечных сечениях балки с присоединенными массами во времени.
Ссылки: С. Д. Пономарев, В. Л. Бидерман, К. К. Лихарев, В. М. Макушин, Н. Н. Малинин, В. И. Феодосьев, Основы современных методов расчета на прочность в машиностроении. Расчеты при динамической нагрузке. Устойчивость. Ползучесть. Москва, Машгиз, 1952, стр. 150.
Исходные данные:
| E = 3.0·106 тс/м2 | - модуль упругости; |
| ν = 0.2 | - коэффициент Пуассона; |
| b = 0.4 м | - ширина прямоугольного поперечного сечения балки; |
| h = 0.8 м | - высота прямоугольного поперечного сечения балки; |
| l = 8.0 м | - длина пролета балки; |
| m = 3.0 тс·с2/м | - значение сосредоточенных масс, присоединенных к балке; |
| P = 76.8 тс | - значение поперечной внезапно приложенной постоянной силы, приложенной к одной из масс; |
| g = 10.00 м/с2 | - значение ускорения свободного падения; |
| I = b·h3/12 = 0.017067 | - момент инерции поперечного сечения балки. |
Конечноэлементная модель: Расчетная схема – плоская рама, 32 стержневых элемента типа 2. Обеспечение граничных условий по свободно опертым торцам балки достигается за счет наложения связей по направлению степени свободы Z. Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связи в узле поперечного сечения оси симметрии балки по направлению степени свободы X. Сосредоточенные массы задаются преобразованием статических узловых нагрузок m·g.
Расчет производится в два этапа: сначала модальным анализом определяются собственные формы и частоты колебаний p, затем методом прямого интегрирования уравнений движения определяются прогибы η и изгибающие моменты M в поперечных сечениях балки с присоединенными массами во времени. Воздействие поперечной внезапно приложенной постоянной силы описывается графиком изменения нагрузки во времени и задается в виде узловой силы, действующей по оси Z общей системы координат с масштабным множителем 1.0 и временем запаздывания 0.0 с. Интервалы между моментами времени графика изменения нагрузки равны Δtint = 0.001571 c (T1/100) и соответствуют шагу интегрирования. При построении графика воздействие поперечной внезапно приложенной постоянной силы принимается со значением P = 76.8 тс во все моменты времени n·Δtint. Продолжительность процесса во времени равна t = 0.3142 с, что соответствует величине удвоенного периода колебаний основного тона 2·T1. Коэффициенты критического демпфирования по 1-й и 2-й собственным частотам приняты с минимальным значением ξ = 0.0001. Коэффициент пересчета для присоединенного статического загружения равен k = 0.981 (формирование масс). Количество узлов в расчетной схеме – 33. При решении используется метод модального интегрирования. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD


Расчетная схема

1-я и 2-я собственные формы колебаний
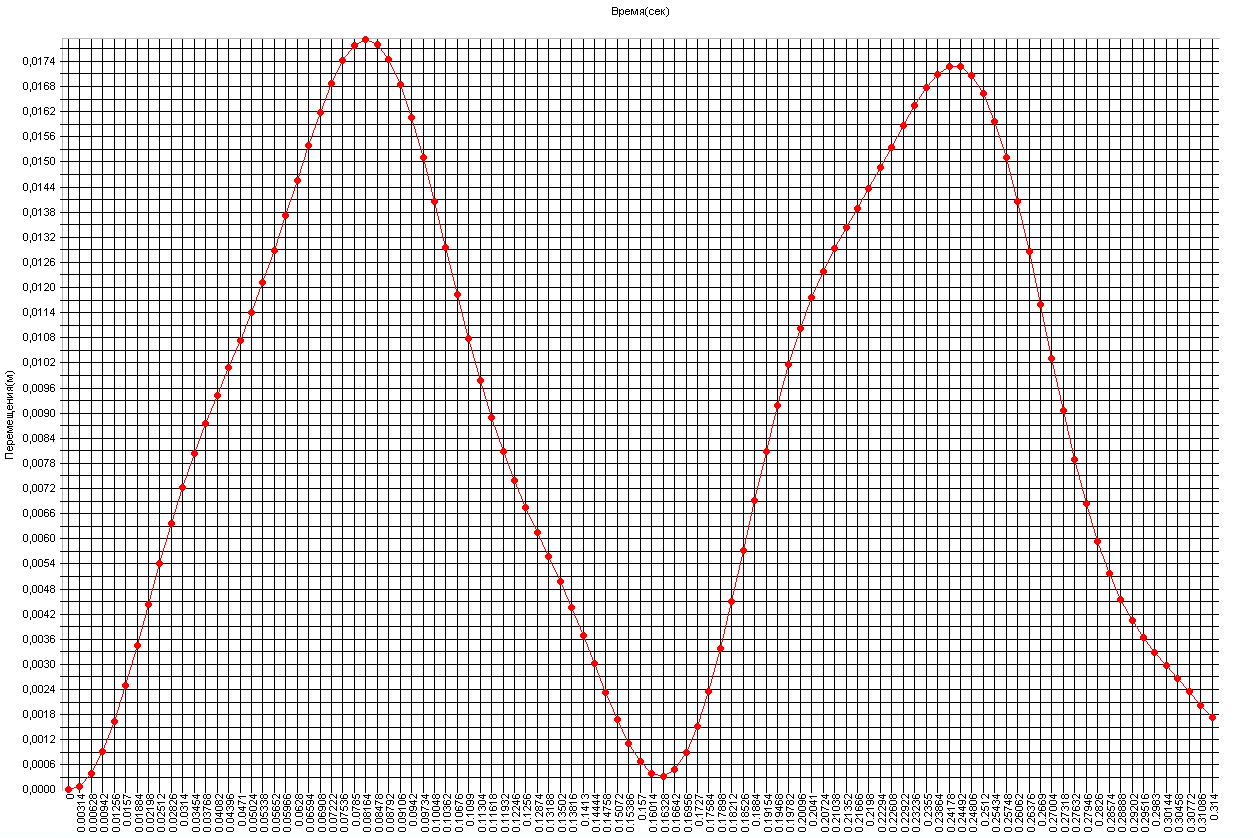
График изменения прогиба η1 в поперечном сечении балки с присоединенной массой, подверженной воздействию поперечной силы, во времени (м)
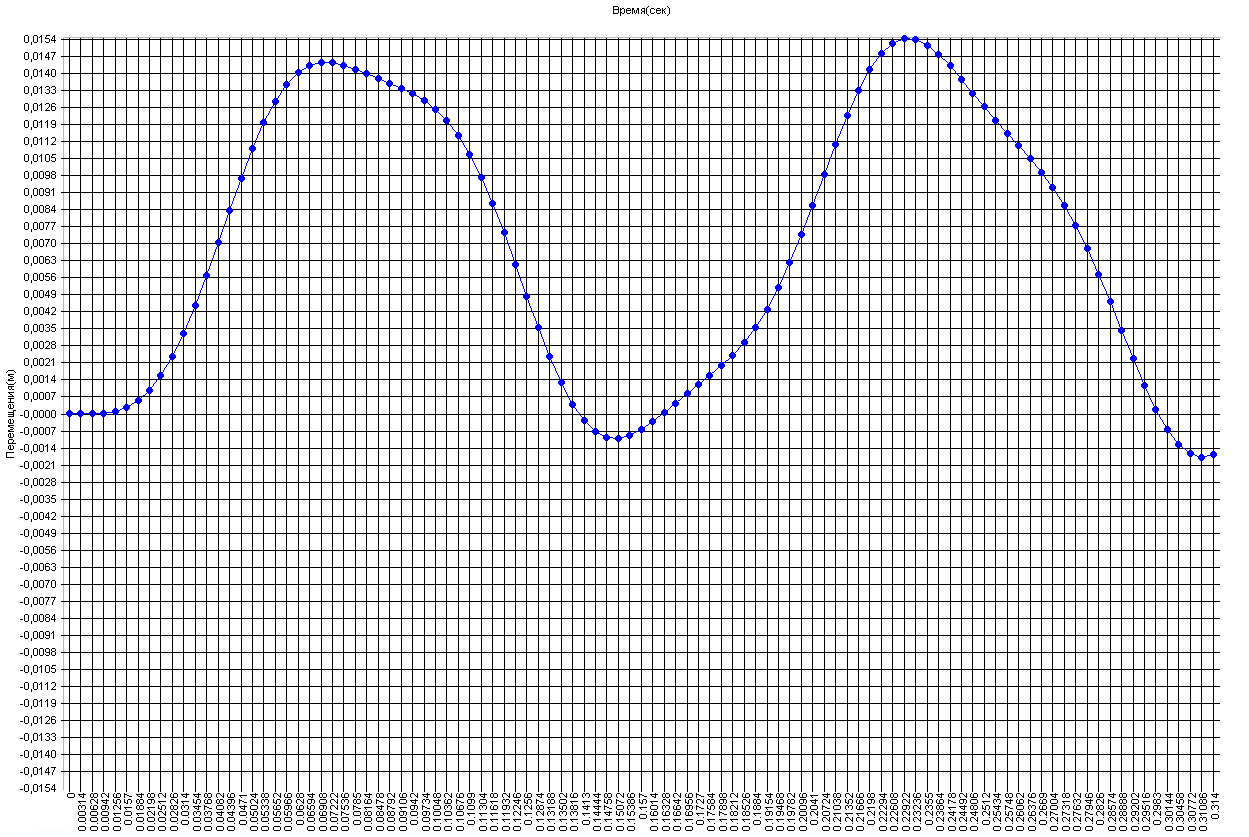
График изменения прогиба η2 в поперечном сечении балки с присоединенной массой, неподверженной воздействию поперечной силы, во времени (м)


Амплитудное значение прогиба η1 в поперечном сечении балки с присоединенной массой, подверженной воздействию поперечной силы и деформированная схема в соответствующий момент (м)


Амплитудное значение прогиба η2 в поперечном сечении балки с присоединенной массой, неподверженной воздействию поперечной силы и деформированная схема в соответствующий момент (м)
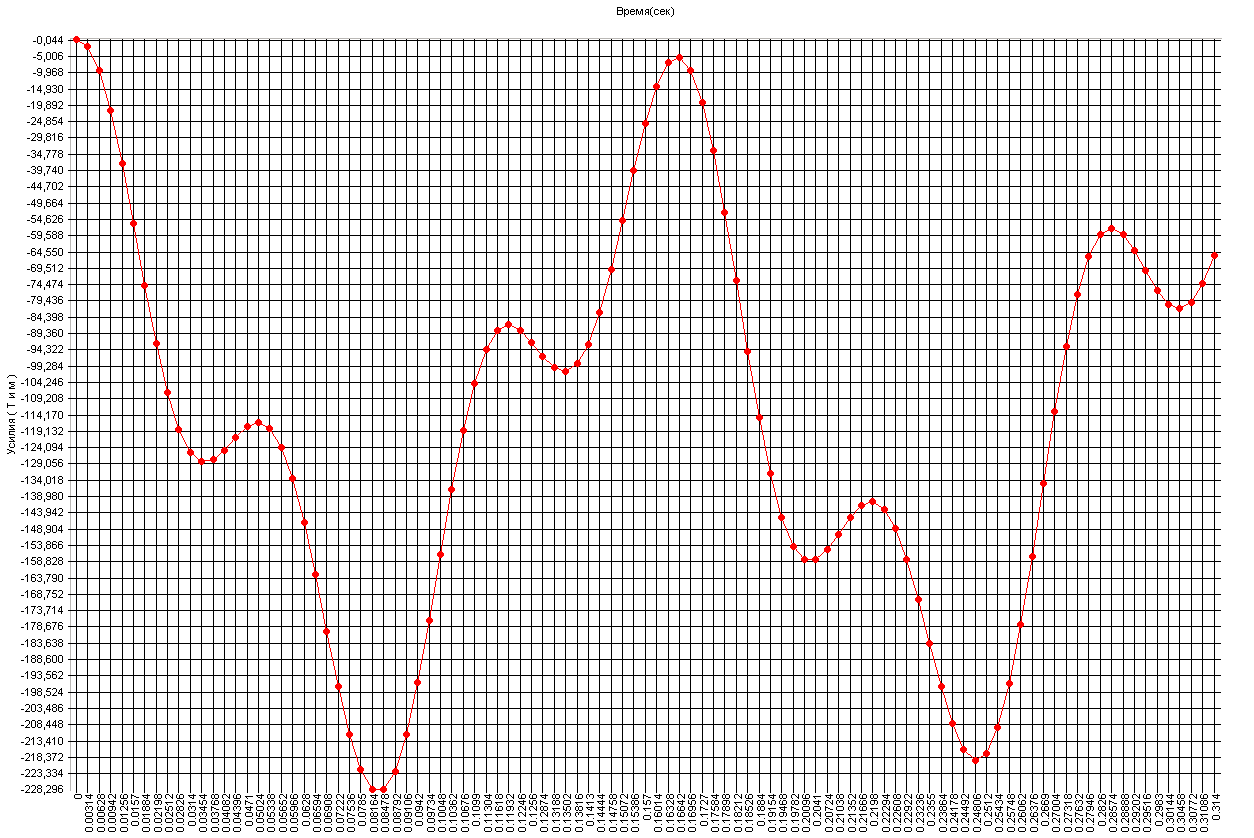
График изменения изгибающего момента M1 в поперечном сечении балки с присоединенной массой, подверженной воздействию поперечной силы, во времени (тм·м)
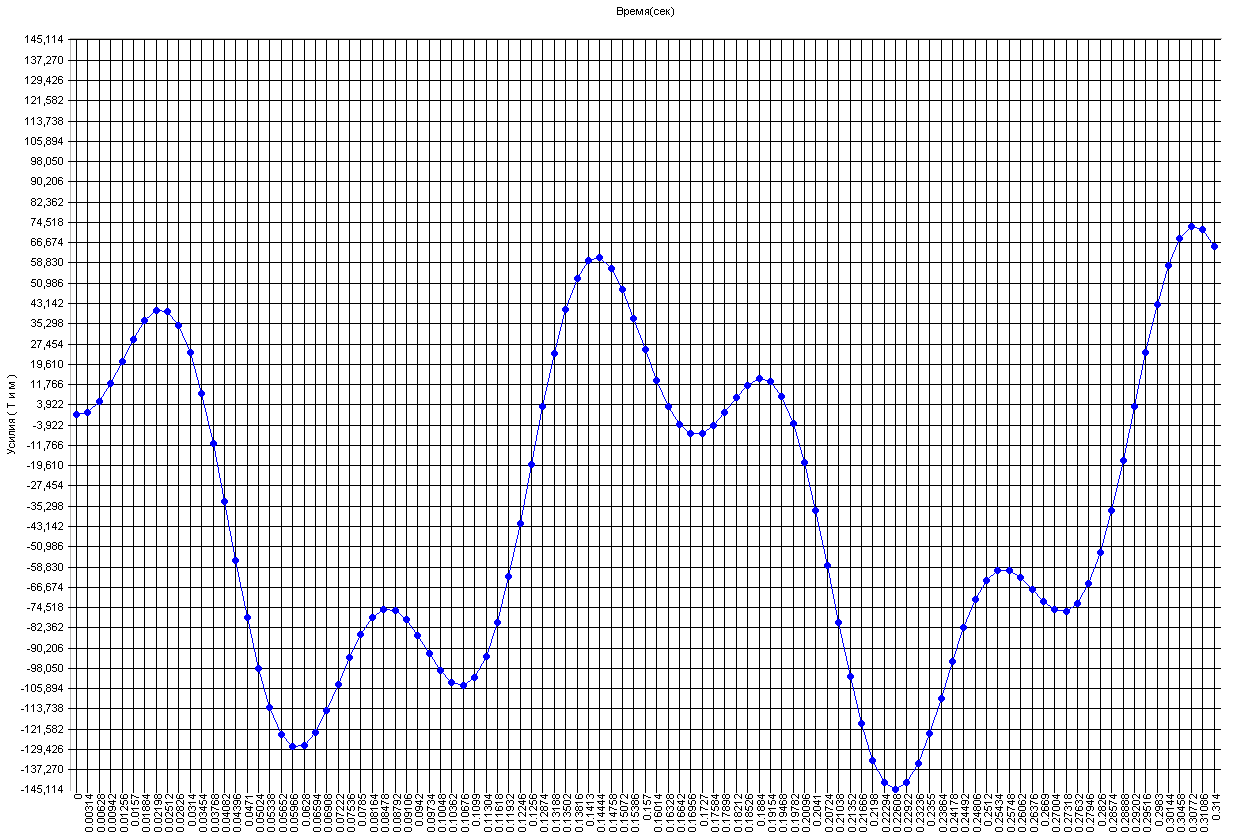
График изменения изгибающего момента M2 в поперечном сечении балки с присоединенной массой, неподверженной воздействию поперечной силы, во времени (тм·м)





Амплитудные значения изгибающего момента M1 в поперечном сечении балки с присоединенной массой, подверженной воздействию поперечной силы (тм·м)





Амплитудные значения изгибающего момента M2 в поперечном сечении балки с присоединенной массой, неподверженной воздействию поперечной силы (тм·м)
Сравнение решений:
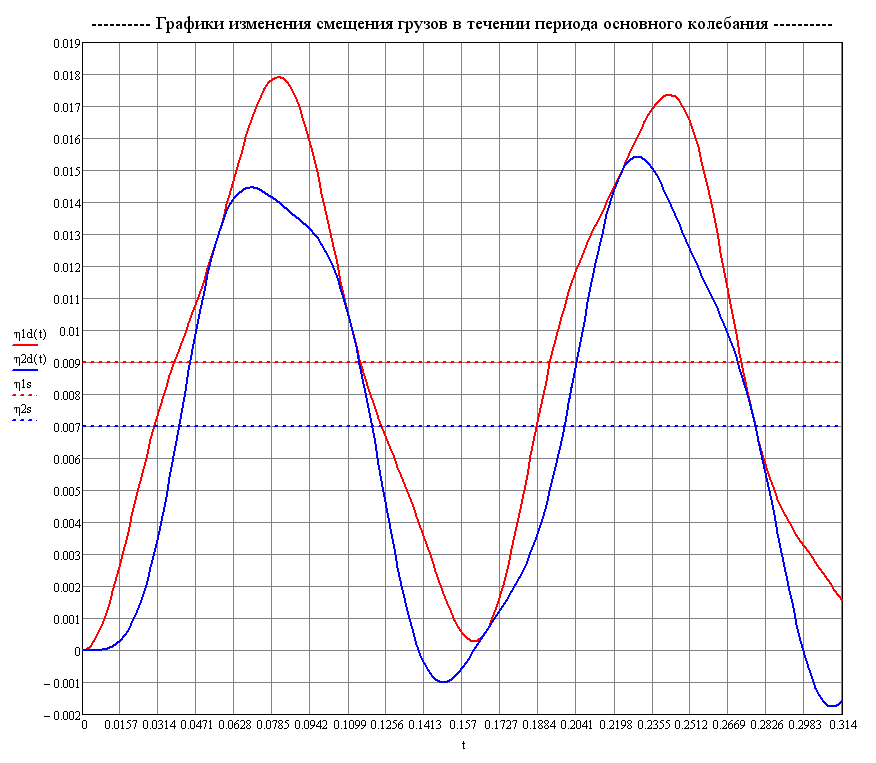
Пунктиром показаны значения статических прогибов
Графики изменения прогибов η1 и η2 в поперечных сечениях балки с присоединенными массами во времени по теоретическому решению (м)
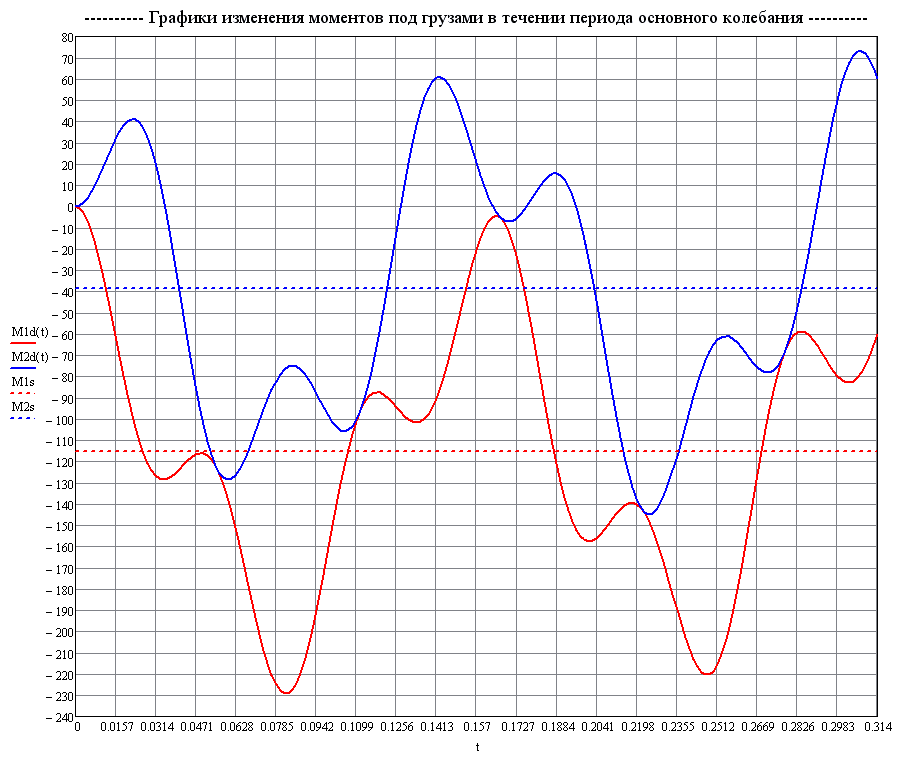
Пунктиром показаны значения статических изгибающих моментов
Графики изменения изгибающих моментов M1 и M2 в поперечных сечениях балки с присоединенными массами во времени по теоретическому решению (тс·м)
Собственные частоты колебаний p, рад/с
|
Форма колебаний |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
1 |
40.000 |
40.000 |
0.00 |
|
2 |
113.137 |
113.137 |
0.00 |
Амплитудное значение прогибов η в поперечных сечениях балки с присоединенными массами, м
|
Узловая масса |
Теория |
SCAD |
|||
|---|---|---|---|---|---|
|
Время, с |
Прогиб, м |
Время, с |
Прогиб, м |
Отклонения, % |
|
|
1 |
0.0809 |
0.017928 |
0.0817 |
0.017911 |
0.09 |
|
2 |
0.0695 |
0.014474 |
0.0707 |
0.014485 |
0.08 |
Амплитудное значение изгибающих моментов M в поперечных сечениях балки с присоединенными массами, тс·м
|
Узловая масса |
Теория |
SCAD |
|||
|---|---|---|---|---|---|
|
Время, с |
Изгибающий момент, тс·м |
Время, с |
Изгибающий момент, тс·м |
Отклонения, % |
|
|
1 |
0.0346 |
-128.426 |
0.0361 |
-128.486 |
0.05 |
|
1 |
0.0493 |
-115.960 |
0.0503 |
-116.387 |
0.37 |
|
1 |
0.0824 |
-229.286 |
0.0833 |
-228.949 |
0.15 |
|
1 |
0.1180 |
-87.419 |
0.1194 |
-86.744 |
0.77 |
|
1 |
0.1334 |
-101.705 |
0.1351 |
-100.782 |
0.91 |
|
2 |
0.0226 |
+41.120 |
0.0236 |
+40.829 |
0.71 |
|
2 |
0.0599 |
-128.638 |
0.0613 |
-128.687 |
0.04 |
|
2 |
0.0849 |
-74.952 |
0.0864 |
-74.957 |
0.01 |
|
2 |
0.1052 |
-105.748 |
0.1068 |
-104.818 |
0.88 |
|
2 |
0.1423 |
+60.864 |
0.1430 |
+61.063 |
0.33 |
Замечания: При аналитическом решении собственные частоты колебаний p свободно опертой балки определяются по формулам:
\[ p_{1} =\sqrt {\frac{48\cdot E\cdot I}{m\cdot l^{3}}} ; \quad p_{2} =\sqrt {\frac{384\cdot E\cdot I}{m\cdot l^{3}}} . \]
При аналитическом решении прогибы η в поперечных сечениях балки с присоединенными массами во времени определяются по формулам:
\[ \eta_{1} \left( t \right)=\frac{P\cdot l^{3}}{768\cdot E\cdot I}\cdot \left[ {8\cdot \left( {1-\cos \left( {p_{1} \cdot t} \right)} \right)+\left( {1-\cos \left( {p_{2} \cdot t} \right)} \right)} \right]; \] \[ \eta_{2} \left( t \right)=\frac{P\cdot l^{3}}{768\cdot E\cdot I}\cdot \left[ {8\cdot \left( {1-\cos \left( {p_{1} \cdot t} \right)} \right)-\left( {1-\cos \left( {p_{2} \cdot t} \right)} \right)} \right]. \]
При аналитическом решении изгибающие моменты M в поперечных сечениях балки с присоединенными массами во времени определяются по формулам:
\[ \eta_{1} \left( t \right)=\frac{P\cdot l^{3}}{768\cdot E\cdot I}\cdot \left[ {8\cdot \left( {1-\cos \left( {p_{1} \cdot t} \right)} \right)+\left( {1-\cos \left( {p_{2} \cdot t} \right)} \right)} \right]; \] \[ \eta_{2} \left( t \right)=\frac{P\cdot l^{3}}{768\cdot E\cdot I}\cdot \left[ {8\cdot \left( {1-\cos \left( {p_{1} \cdot t} \right)} \right)-\left( {1-\cos \left( {p_{2} \cdot t} \right)} \right)} \right]. \]
