Свободно опертая балка с распределенной массой под действием постоянной поперечной силы, перемещающейся вдоль пролета балки с постоянной скоростью

Цель: Определение деформированного состояния свободно опертой балки с распределенной массой от воздействия постоянной поперечной силы, перемещающейся вдоль пролета балки с постоянной скоростью.

Файлы с исходными данными:

DIN_B_ML1.spr График_DIN_B_ML1.txt	Воздействие постоянной поперечной силы, перемещающейся вдоль пролета балки, задается в виде сил, приложенных во всех узлах расчетной схемы по следующему варианту: Время запаздывания для каждой из узловых сил различно. График, описывающий изменение нагрузки во времени, является единым для всех узловых сил.
DIN_B_ML2.spr График_DIN_B_ML2_2.txt График_DIN_B_ML2_3.txt График_DIN_B_ML2_4.txt График_DIN_B_ML2_5.txt График_DIN_B_ML2_6.txt График_DIN_B_ML2_7.txt График_DIN_B_ML2_8.txt График_DIN_B_ML2_9.txt График_DIN_B_ML2_10.txt График_DIN_B_ML2_11.txt График_DIN_B_ML2_12.txt График_DIN_B_ML2_13.txt График_DIN_B_ML2_14.txt График_DIN_B_ML2_15.txt График_DIN_B_ML2_16.txt График_DIN_B_ML2_17.txt График_DIN_B_ML2_18.txt График_DIN_B_ML2_19.txt График_DIN_B_ML2_20.txt График_DIN_B_ML2_21.txt График_DIN_B_ML2_22.txt График_DIN_B_ML2_23.txt График_DIN_B_ML2_24.txt График_DIN_B_ML2_25.txt График_DIN_B_ML2_26.txt График_DIN_B_ML2_27.txt График_DIN_B_ML2_28.txt График_DIN_B_ML2_29.txt График_DIN_B_ML2_30.txt График_DIN_B_ML2_31.txt График_DIN_B_ML2_32.txt	Воздействие постоянной поперечной силы, перемещающейся вдоль пролета балки, задается в виде сил, приложенных во всех узлах расчетной схемы по следующему варианту: Время запаздывания для всех узловых сил является единым. Каждой узловой силе соответствует свой график, описывающий изменение нагрузки во времени.

DIN_B_ML1.spr
График_DIN_B_ML1.txt

Воздействие постоянной поперечной силы, перемещающейся вдоль пролета балки, задается в виде сил, приложенных во всех узлах расчетной схемы по следующему варианту:

Время запаздывания для каждой из узловых сил различно. График, описывающий изменение нагрузки во времени, является единым для всех узловых сил.

Время запаздывания для всех узловых сил является единым. Каждой узловой силе соответствует свой график, описывающий изменение нагрузки во времени.

Формулировка задачи: Вдоль пролета свободно опертой балки постоянного сечения с равномерно распределенной массой μ перемещается с постоянной скоростью v постоянная поперечная сила P. Определить собственные формы и частоты колебаний p свободно опертой балки, а также прогиб η в поперечном сечении середины пролета балки во времени.

Ссылки: С. П. Тимошенко, Курс теории упругости, под редакцией Э. И. Григолюка, Киев, Наукова думка, 1972, стр. 345.

Исходные данные:

E = 3.0·10⁶ тс/м²	- модуль упругости;
ν = 0.2	- коэффициент Пуассона;
b = 0.4 м	- ширина прямоугольного поперечного сечения балки;
h = 0.8 м	- высота прямоугольного поперечного сечения балки;
l = 8.0 м	- длина пролета балки;
γ = 2.5 тс/м³	- объемный вес материала балки;
P = 76.8 тс	- значение постоянной силы, перемещающейся вдоль пролета балки;
g = 10.00 м/с²	- значение ускорения свободного падения;

μ = 2.5·0.4·0.8/10.0 = 0.08 тс·с²/м²	- значение равномерно распределенной массы балки;
I = 0.4·(0.8)³/12 = 0.017067 м⁴	- момент инерции поперечного сечения балки.

Скорость перемещения постоянной силы v принимается в зависимости от значений длины пролета балки и периода основного тона собственных колебаний балки T₁:

v = l / T₁.

Конечноэлементная модель: Расчетная схема – балочный ростверк / плита, 32 стержневых элемента типа 3. Обеспечение граничных условий по свободно опертым торцам балки достигается за счет наложения связей по направлению степени свободы Z. Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связи в узле поперечного сечения оси симметрии балки по направлению степени свободы UX. Распределенная масса задается преобразованием статической нагрузки от собственного веса балки μ·g.

Расчет производится в два этапа: сначала модальным анализом определяются собственные формы и частоты колебаний p, затем методом прямого интегрирования уравнений движения определяются прогибы η в поперечном сечении середины пролета балки во времени.

Воздействие постоянной поперечной силы, перемещающейся вдоль пролета балки, задается в виде сил, приложенных во всех узлах расчетной схемы по оси Z общей системы координат с масштабным множителем 1.0 по двум вариантам:

Время запаздывания для каждой из узловых сил различно и определяется как t₀ = 2·(m-1)·Δt_int, где m – количество конечных элементов, отсчитываемое от опорного узла балки до рассматриваемого по ходу движения нагрузки. График, описывающий изменение нагрузки во времени, является единым для всех узловых сил. При построении графика узловая сила принимается с последовательными значениями: 0; 0.5·P; P; 0.5·P; 0 в моменты времени: 0; Δt_int; 2·Δt_int; 3·Δt_int; 4·Δt_int; 5·Δt_int, отсчитываемые от времени запаздывания t₀, в дальнейшие моменты времени узловая сила равна 0.
Время запаздывания для всех узловых сил является единым и равно t₀ = 0. Каждой узловой силе соответствует свой график, описывающий изменение нагрузки во времени. При построении графика узловая сила в моменты времени от 0 до 2·(m-1)·Δt_int равна 0, в моменты времени от 2·(m-1)·Δt_int до 2·(m+1)·Δt_int включительно принимается с последовательными значениями: 0; 0.5·P; P; 0.5·P; 0, в дальнейшие моменты времени узловая сила равна 0, где m – количество конечных элементов, отсчитываемое от опорного узла балки до рассматриваемого по ходу движения нагрузки.

Для обоих вариантов задания воздействия подвижной нагрузки интервалы между моментами времени графиков изменения нагрузки равны времени прохождения половины расстояния между смежными узлами расчетной схемы со скоростью v: Δt_int = L / (2·n·v) = T₁ / (2·n) и соответствуют шагу интегрирования, где n – количество конечных элементов в расчетной схеме. Продолжительность процесса равна времени прохождения подвижной нагрузки по пролету балки l со скоростью v: t = l/v =T₁. Коэффициенты критического демпфирования по 1-й и 2-й собственным частотам приняты с минимальным значением ξ = 0.0001. Коэффициент пересчета для присоединенного статического загружения равен k = 0.981 (формирование масс). Количество узлов в расчетной схеме – 33. При решении используется метод модального интегрирования. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.

Результаты решения в SCAD

Расчетная схема

1-я -- 16-я собственные формы колебаний

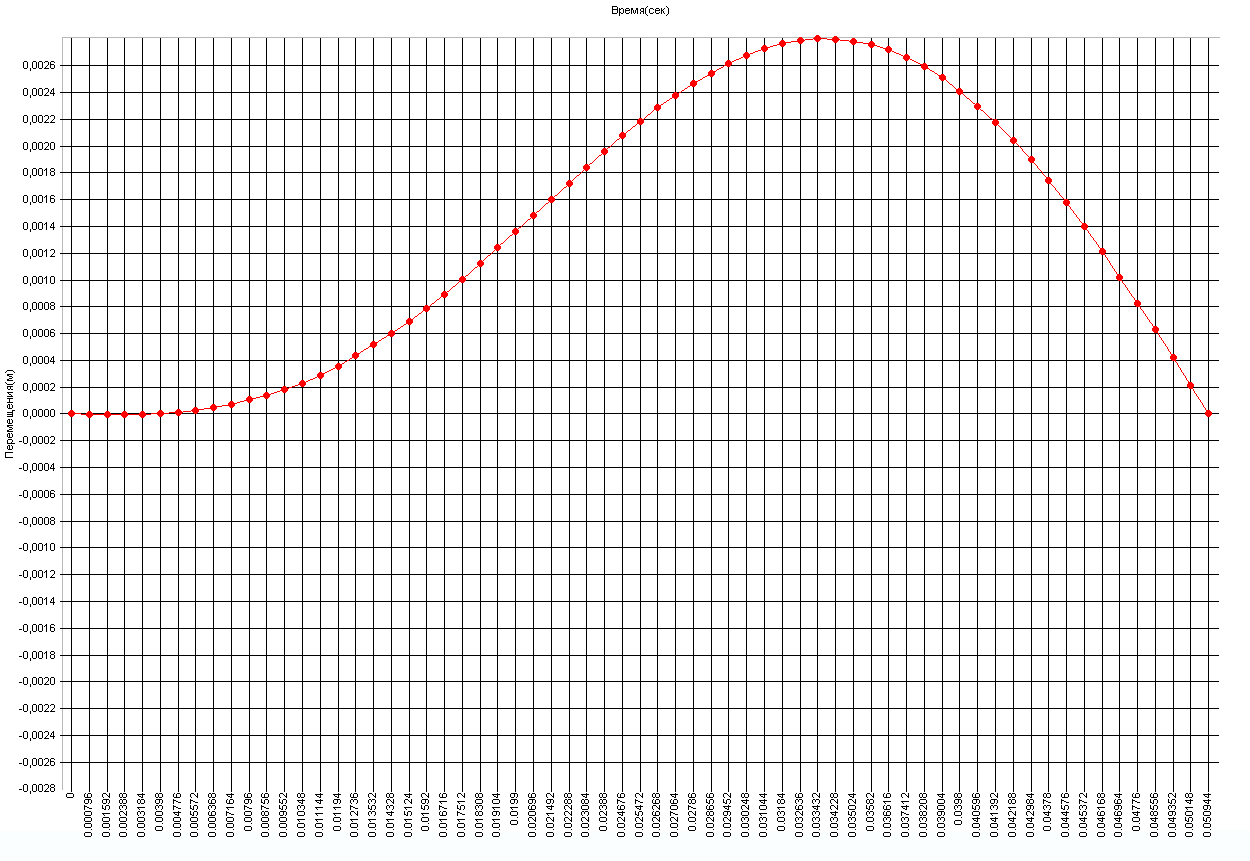
График изменения прогиба η в поперечном сечении середины пролета балки во времени (м)

Амплитудное значение прогиба η в поперечном сечении середины пролета балки и деформированные схемы в соответствующий момент времени (м)

Сравнение решений:

Собственные частоты колебаний p, рад/с

Форма колебаний	Теория	SCAD	Отклонения, %
1	123.370	123.370	0.00
2	493.480	493.480	0.00
3	1110.330	1110.325	0.00
4	1973.921	1973.887	0.00
5	3084.251	3084.120	0.00
6	4441.322	4440.919	0.01
7	6045.133	6044.087	0.02
8	7895.684	7893.275	0.03
9	9992.974	9987.907	0.05
10	12337.005	12327.069	0.08
11	14927.777	14909.367	0.12
12	17765.288	17732.721	0.18
13	20849.539	20794.097	0.27
14	24180.531	24089.155	0.38
15	27758.262	27611.778	0.53
16	31582.734	31353.470	0.73

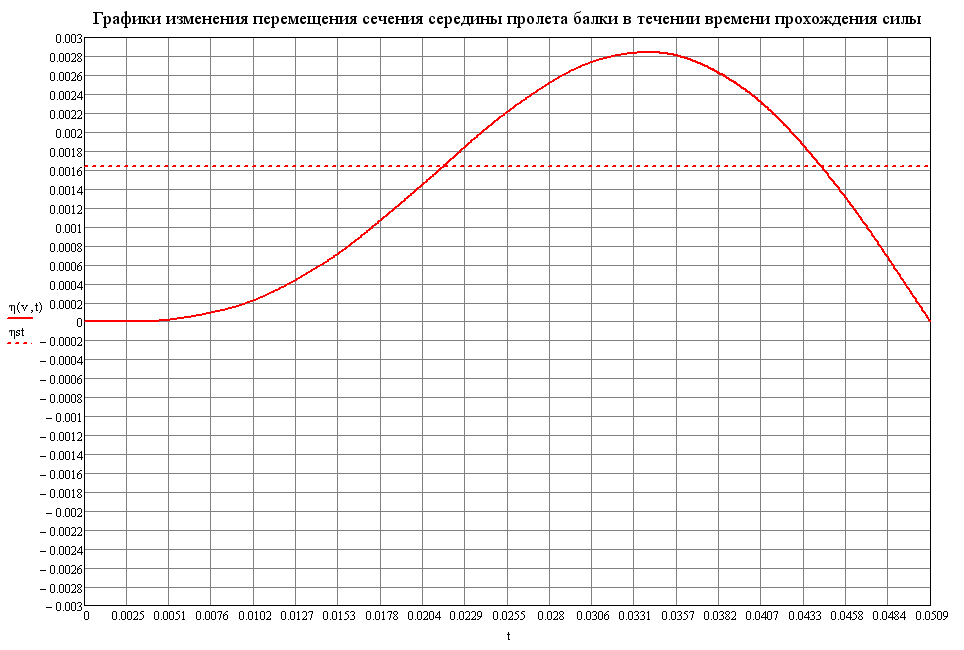
Пунктиром показано значение статического прогиба

График изменения прогиба η в поперечном сечении середины пролета балки во времени по теоретическому решению (м)

Амплитудное значение прогиба η в поперечном сечении середины пролета балки, м

Теория		SCAD
Время, с	Прогиб, м	Время, с	Прогиб, м	Отклонение, %
0.0339	0.002842	0.0334	0.002837	0.18

Замечания: При аналитическом решении собственные частоты колебаний p свободно опертой балки определяются по формуле:

\[ \frac{n^{2}\cdot \pi^{2}}{l^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} , \]

где n = 1, 2, 3, 4, … – номер формы собственных колебаний.

При аналитическом решении прогибы η в поперечном сечении середины пролета балки во времени определяются по формуле:

\[ \eta \left( t \right)=\frac{2\cdot P\cdot l^{3}}{\pi^{4}\cdot E\cdot I}\cdot \sum\limits_{n=1} {\left[ {\frac{\sin \left( {\frac{n\cdot \pi }{2}} \right)}{n^{4}\cdot \left( {1-\frac{\mu \cdot l^{2}\cdot v^{2}}{n^{2}\cdot \pi^{2}\cdot E\cdot I}} \right)}\cdot \left( {\sin \left( {\frac{n\cdot \pi \cdot v}{l}\cdot t} \right)-\frac{l\cdot v}{n\cdot \pi }\cdot \sqrt {\frac{\mu }{E\cdot I}} \cdot \sin \left( {\frac{n^{2}\cdot \pi ^{2}}{l^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)} \right)} \right]} ; \]