Свободно опертая балка с распределенной массой под действием кинематического возмущения опор (сейсмическое воздействие)
Цель: Определение напряженно-деформированного состояния свободно опертой балки с распределенной массой от воздействия кинематического возмущения опор.
Файл с исходными данными: DIN_B_SL.spr, DIN_B_SL.spc
Формулировка задачи: Свободно опертая балка постоянного сечения с равномерно распределенной массой μ подвергается воздействию кинематического возмущения опор по заданной акселерограмме:
\[ \ddot{{z}}(t)=\ddot{{z}}_{s0} \cdot \left( {1-\frac{t}{t_{d} }} \right). \]
Определить собственную форму и частоту колебаний основного тона f свободно опертой балки, а также максимальные амплитудные значения прогиба z и изгибающего момента M в поперечном сечении середины пролета балки по времени t.
Ссылки: John M. Biggs, Introduction to Structural Dynamics, McGraw-Hill Book Companies, New York, 1964, p.262.
Исходные данные:
| E = 3.0·107 psi = 2.1092·107тс/м2 | - модуль упругости; |
| I = 333.333 in4 = 138.7448·10-6 м4 | - момент инерции поперечного сечения балки. |
| h = 14 in = 0.3556 м | - высота поперечного сечения балки; |
| L = 240 in = 6.0960 м | - длина пролета балки; |
| μ = 0.2 lb·sec2/in2 = 0.1406 тс·с2/м2 | - значение равномерно распределенной массы балки; |
| \(\ddot{{z}}_{s0}=\) ±386.2200 in/sec2 = ±9.81 м/с2 | - амплитудные значения ускорения опор по акселерограмме; |
| td = 0.10 sec = 0.10 с | - полуинтервал воздействия кинематического возмущения опор; |
| g = 386.2200 in/sec2 =9.81 м/с2 | - значение ускорения свободного падения. |
Конечноэлементная модель: Расчетная схема – балочный ростверк / плита, 32 стержневых элемента типа 3. Обеспечение граничных условий по свободно опертым торцам балки достигается за счет наложения связей по направлению степени свободы Z. Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связи в узле поперечного сечения оси симметрии балки по направлению степени свободы UX. Распределенная масса задается преобразованием статической нагрузки от собственного веса балки μ·g.
Кинематическое возмущение опор описывается графиком изменения ускорения во времени (акселерограммой) и задается в виде воздействия по оси Z общей системы координат (направляющие косинусы к осям X, Y, Z: 0.00, 0.00, 1.00) с масштабным множителем к значениям акселерограммы, равным 1.00. Высота конструкции балки на схеме сориентирована по оси Z общей системы координат. Коэффициент диссипации (коэффициент поглощения энергии колебаний) принят с минимальным значением ξ = 0.000001. Интервалы между моментами времени графика ускорения во времени равны Δt = 0.01 c. При построении графика ускорение принимается со значениями \( \ddot{z}(t) = \ddot{z_{s0}}(t)\left(1-n\frac{\Delta t}{t_d}\right) \) в моменты времени n·Δt. Коэффициент пересчета для присоединенного статического загружения равен k = 1.000 (формирование масс). Количество узлов в расчетной схеме – 33. При решении используется метод модального интегрирования. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD

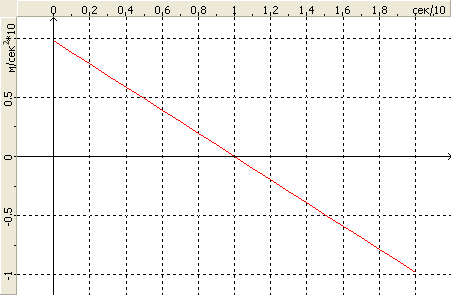
Расчетная схема и заданная акселерограмма

1-я собственная форма колебаний


Амплитудное значение прогиба z в поперечном сечении середины пролета балки и деформированная схема в соответствующий момент времени (м)

Амплитудное значение изгибающего момента M в поперечном сечении середины пролета балки (тм·м)
Сравнение решений:
Собственная частота колебаний основного тона f, Гц
|
Форма колебаний |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
1 |
6.098 |
6.101 |
0.05 |
Максимальное амплитудное значение прогиба z в поперечном сечении середины пролета балки, м
|
Теория |
SCAD |
||
|---|---|---|---|
|
Время, с |
Прогиб, м |
Прогиб, м |
Отклонения, % |
|
0.0163982 |
-0.013951 |
-0.013841 |
0.80 |
Максимальное амплитудное значение изгибающего момента M в поперечном сечении середины пролета балки, тс·м
|
Теория |
SCAD |
||
|---|---|---|---|
|
Время, с |
Изгибающий момент, тс·м |
Изгибающий момент, тс·м |
Отклонения, % |
|
0.0163982 |
10.843 |
10.766 |
0.73 |
Замечания: При аналитическом решении собственная частота колебаний основного тона f свободно опертой балки определяется по формуле:
\[ f=\frac{\pi }{2\cdot L^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \quad . \]
При аналитическом решении прогиб z и изгибающий момент M в поперечном сечении середины пролета балки во времени определяются по формуле:
\[z\left( t \right)=\frac{4\cdot \ddot{{z}}_{s0} \cdot L^{4}\cdot \mu }{\pi ^{5}\cdot E\cdot I}\cdot \left[ {1-\cos \left( {\frac{\pi^{2}}{L^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)+\frac{L^{2}}{\pi^{2}\cdot t_{d} }\cdot \sqrt {\frac{\mu }{E\cdot I}} \cdot \sin \left( {\frac{\pi ^{2}}{L^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)-\frac{1}{t_{d} }\cdot t} \right]; \quad при \quad t\le 2\cdot t_{d}; \] \[M\left( t \right)=\frac{4\cdot \ddot{{z}}_{s0} \cdot L^{2}\cdot \mu }{\pi ^{3}}\cdot \left[ {1-\cos \left( {\frac{\pi^{2}}{L^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)+\frac{L^{2}}{\pi^{2}\cdot t_{d} }\cdot \sqrt {\frac{\mu }{E\cdot I}} \cdot \sin \left( {\frac{\pi ^{2}}{L^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)-\frac{1}{t_{d} }\cdot t} \right]; \quad при \quad t\le 2\cdot t_{d} .\]
