Консольная балка под действием сосредоточенной нагрузки
Цель: Расчет на изгиб в силовой плоскости под сосредоточенной силой, без учета деформаций поперечного сдвига. Проверяются значения максимальных поперечного перемещения, угла поворота и изгибающего момента.
Файл с исходными данными: 4_1.spr
Формулировка задачи: Консольная балка нагружается на свободном конце сосредоточенной силой Р. Определить максимальные значения поперечного перемещения w, угла поворота θ и изгибающего момента М.
Ссылки: Писаренко Г.С., Яковлев А.П., Матвеев В.В., Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988, стр. 263.
Исходные данные:
| E = 2.0·1011 Па | - модуль упругости, |
| ν = 0.3 | - коэффициент Пуассона, |
| L = 3 м | - длина балки; |
| I = 2.44·10-6 м4 | - момент инерции поперечного сечения; |
| Р = 5 кН | - значение сосредоточенной силы. |
Конечноэлементная модель: Расчетная схема – система общего вида, 10 стержневых элементов типа 5, 11 узлов.
Результаты решения в SCAD:

Эпюра изгибающего момента М (кН·м)
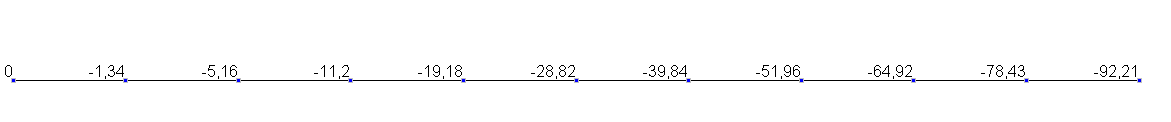
Значения поперечных перемещений w(мм)

Значения углов поворота θ (рад)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Поперечное перемещение w, мм |
-92.21 |
-92.21 |
0.00 |
|
Угол поворота θ, рад |
0.04611 |
0.04611 |
0.00 |
|
Изгибающий момент М, кН·м |
-15.0 |
-15.0 |
0.00 |
Замечания: При аналитическом решении максимальные значения поперечного перемещения w, угла поворота θ и изгибающего момента М определяются по следующим формулам:
\[ w=-\frac{P\cdot L^{3}}{3\cdot E\cdot I}; \quad \theta =\frac{P\cdot L^{2}}{2\cdot E\cdot I}; \quad M=-P\cdot L. \]
