Свободные колебания круговой шарнирно опертой по контуру пластины
Цель: Модальный анализ круговой шарнирно опертой по контуру пластины.
Файл с исходными данными: 5.7.spr
Формулировка задачи: Определить собственные формы и частоты колебаний ω круговой шарнирно опертой по контуру пластины с плотностью материала ρ.
Ссылки: В. Н. Челомей, Вибрации в технике, Справочник в шести томах: В. В. Болотин, Том 1, Колебания линейных систем, Москва, Машиностроение, 1978, стр. 207.
Исходные данные:
| E = 2.06·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 7.85 т/м3 | - плотность материала; |
| h = 0.01 м | - толщина пластины; |
| R = 0.5 м | - наружный радиус пластины. |
Конечноэлементная модель: Расчетная схема – балочный ростверк / плита, 1080 четырехузловых элементов плиты типа 20 и 72 трехузловых элемента плиты типа 15. Сетка конечных элементов разбита с шагом 0.03125 м в радиальном направлении и с шагом 5.0º в тангенциальном направлении. Обеспечение граничных условий достигается за счет наложения связей по направлению степени свободы Z по наружному контуру пластины. Распределенная масса задается преобразованием статической нагрузки от собственного веса пластины ow = γ∙h, где γ = ρ∙g = 77.01 кН/м3. Количество узлов в расчетной схеме – 1153. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD
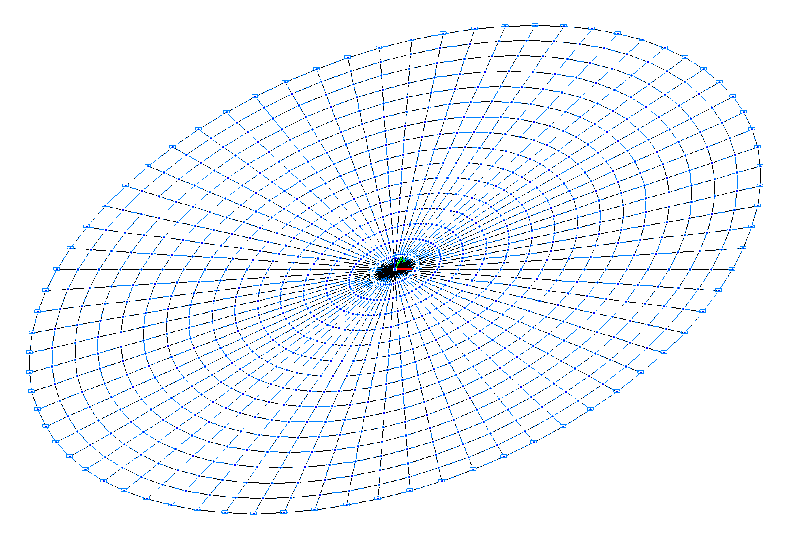
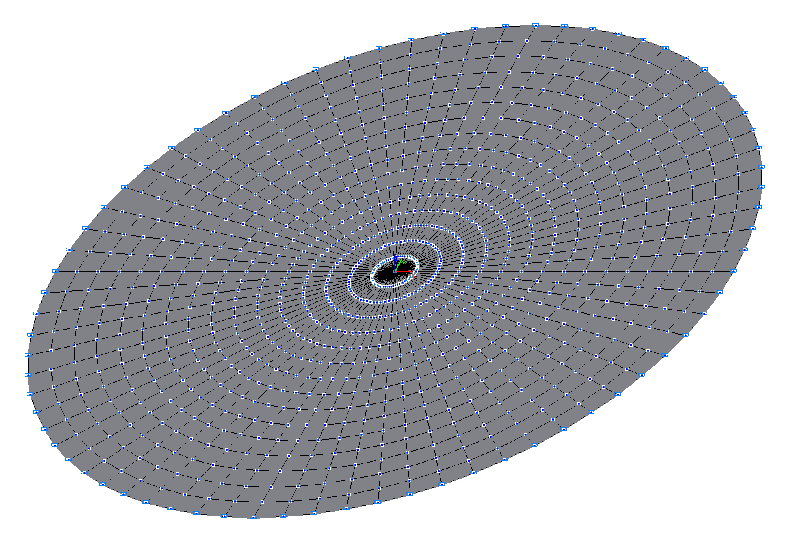
Расчетная схема
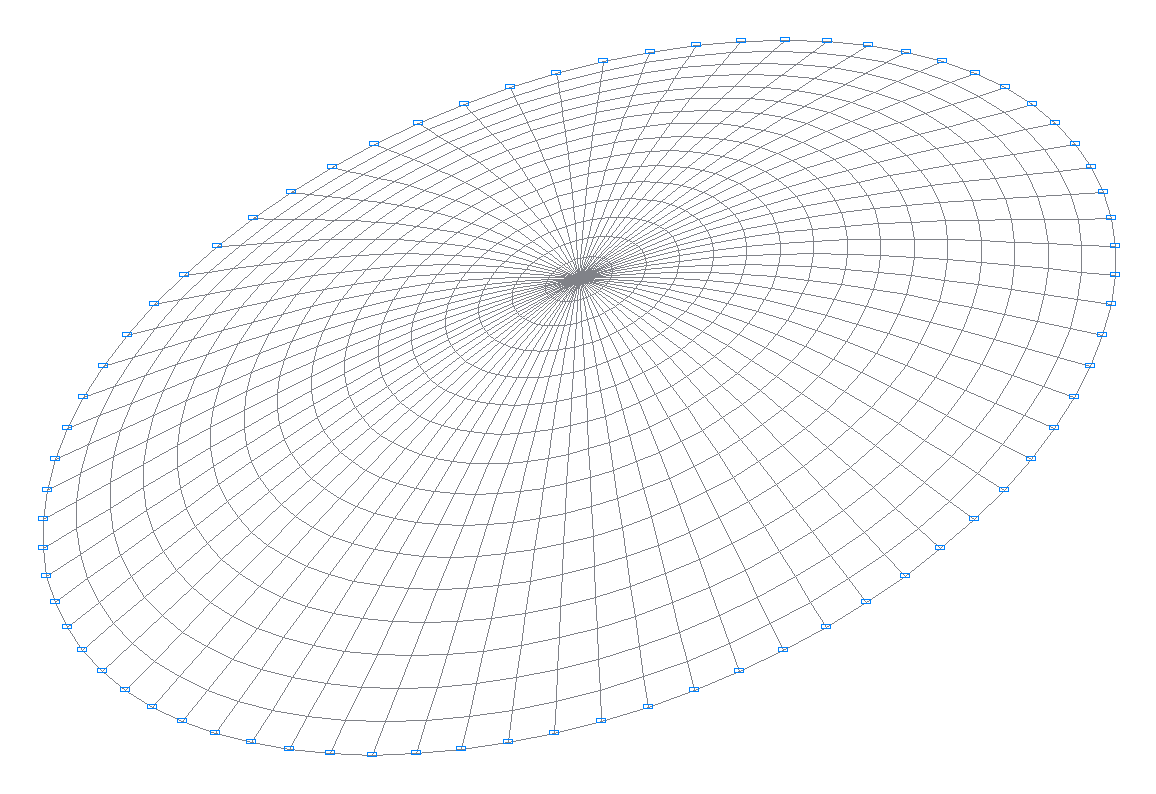
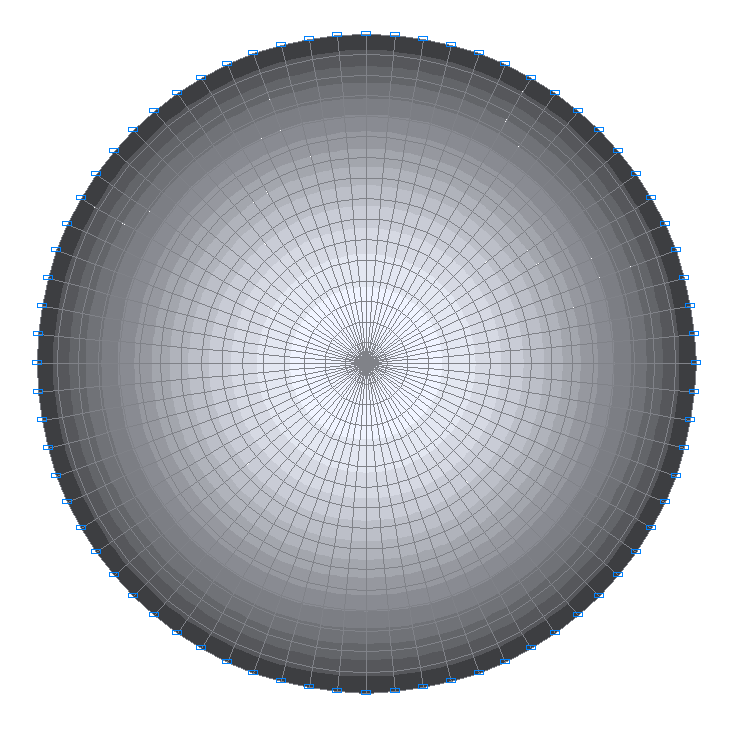
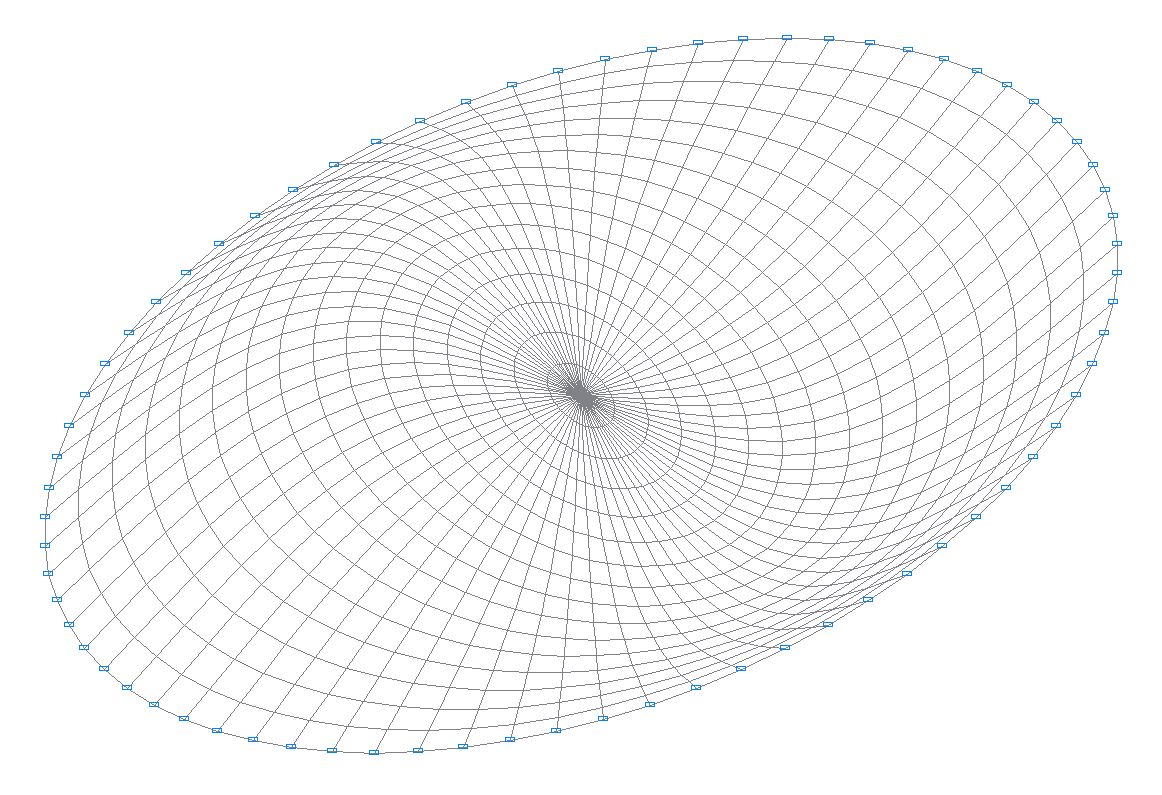
1-я собственная форма колебаний
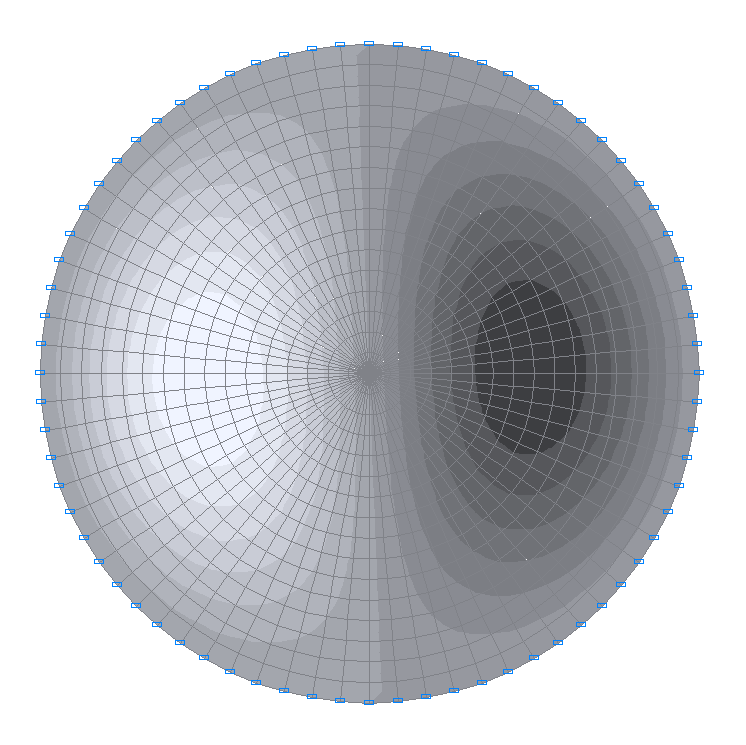

2-я собственная форма колебаний
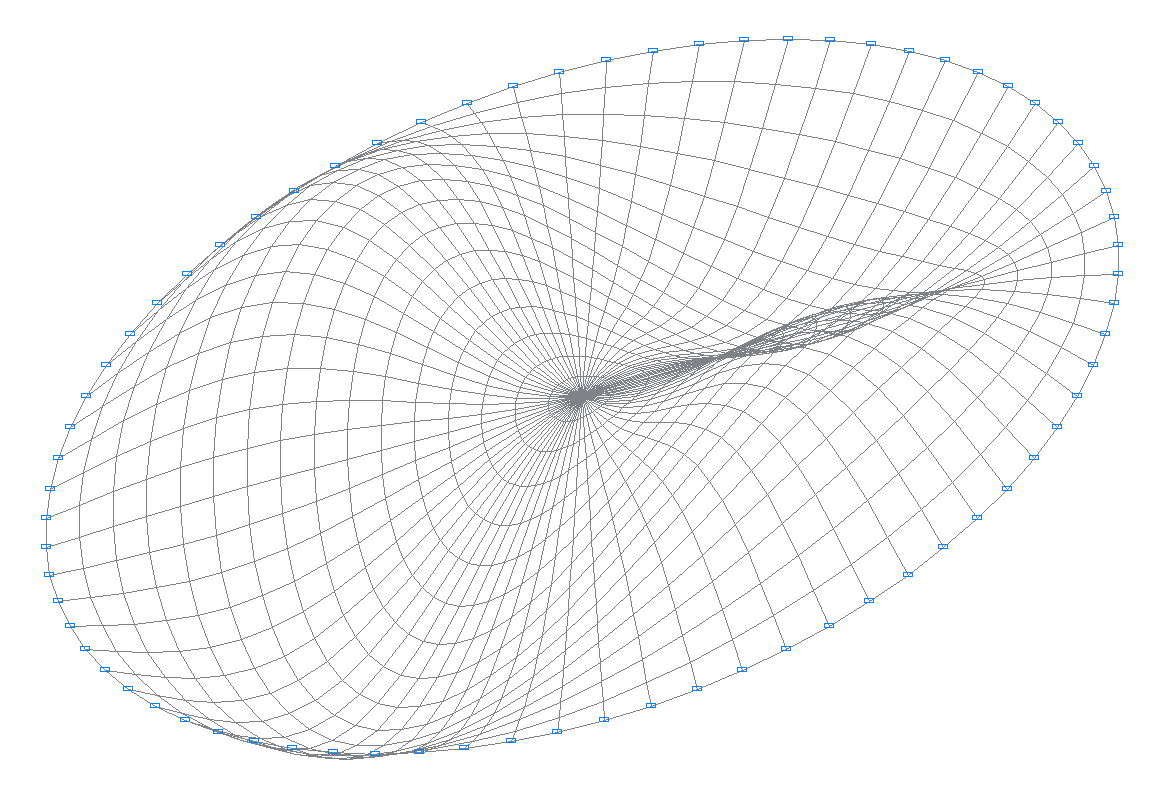
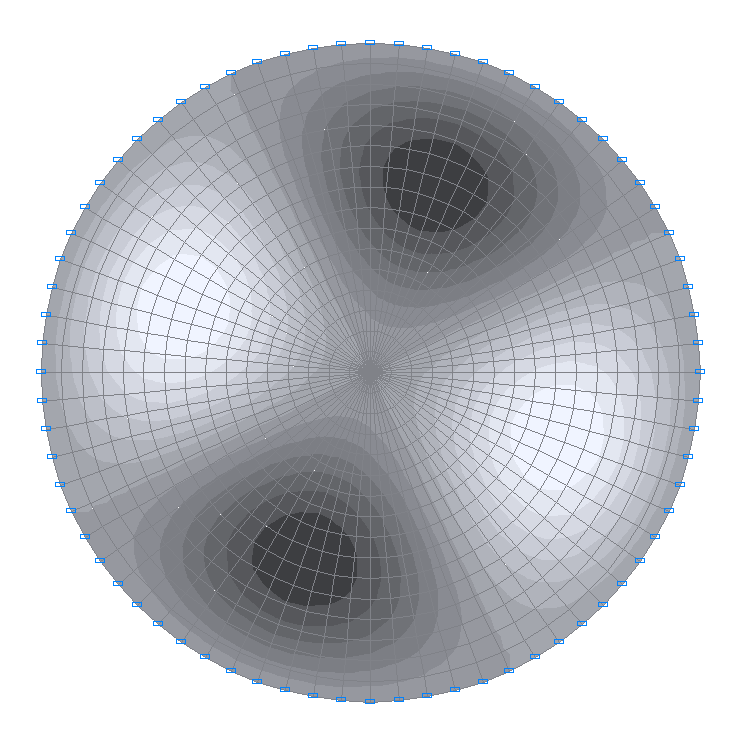

4-я собственная форма колебаний
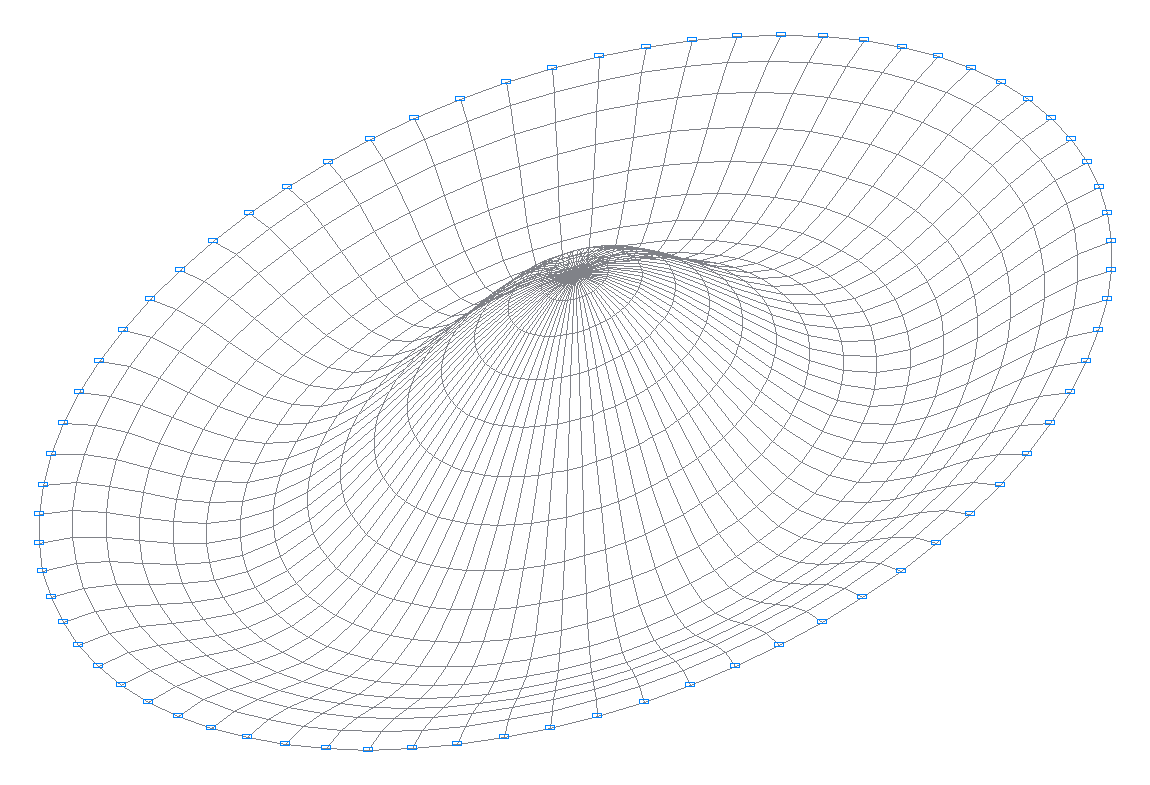
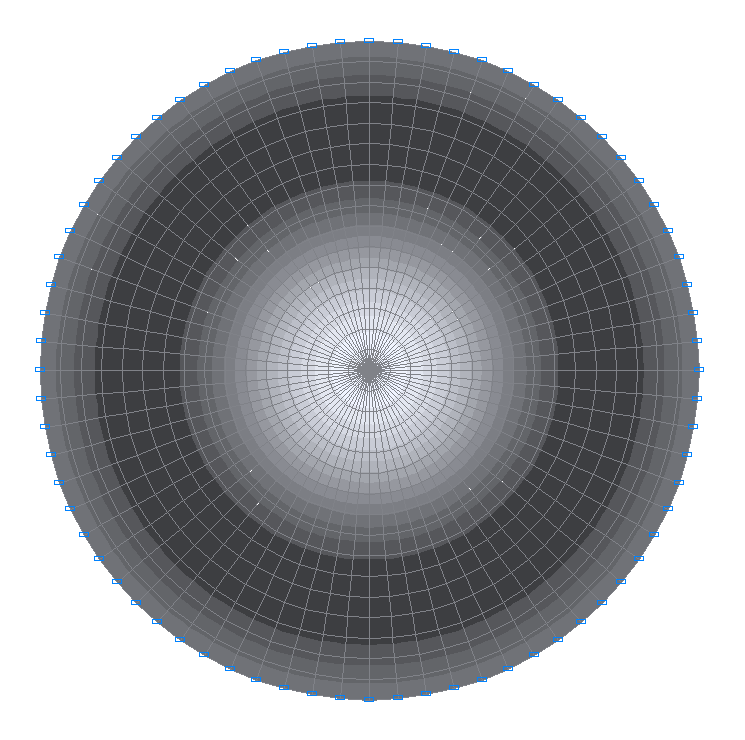

6-я собственная форма колебаний
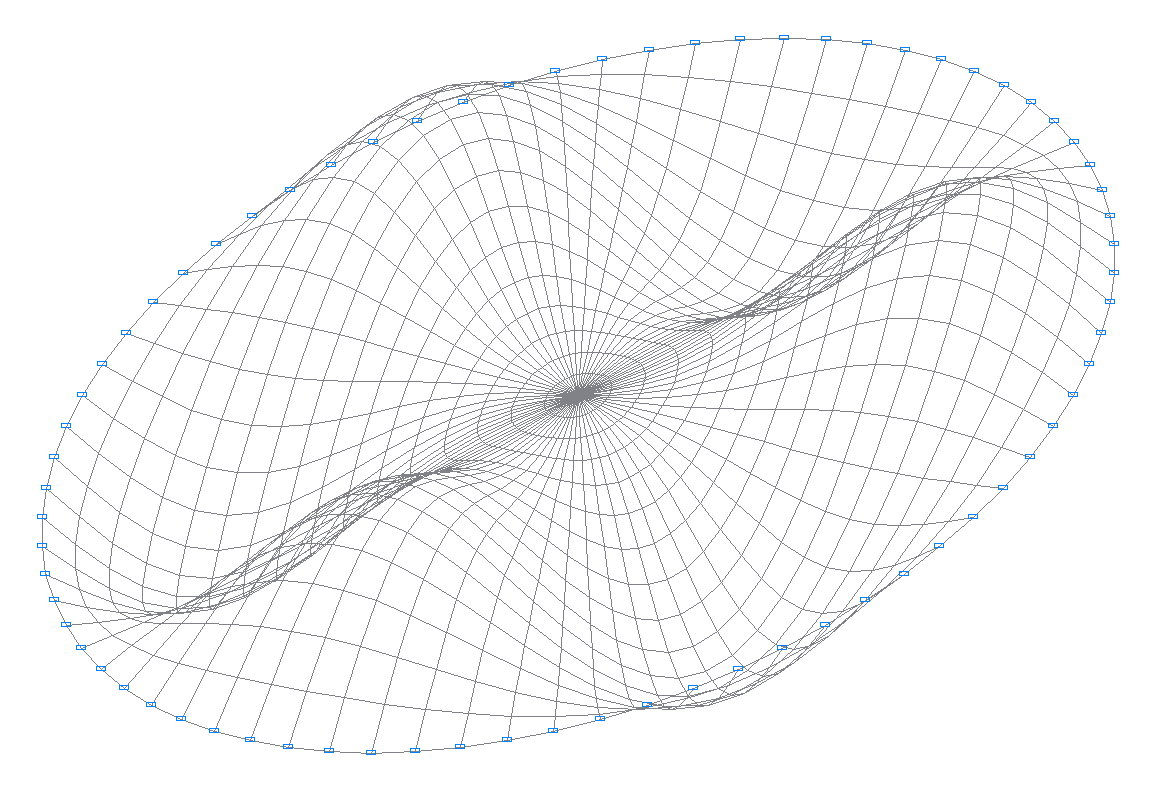

7-я собственная форма колебаний
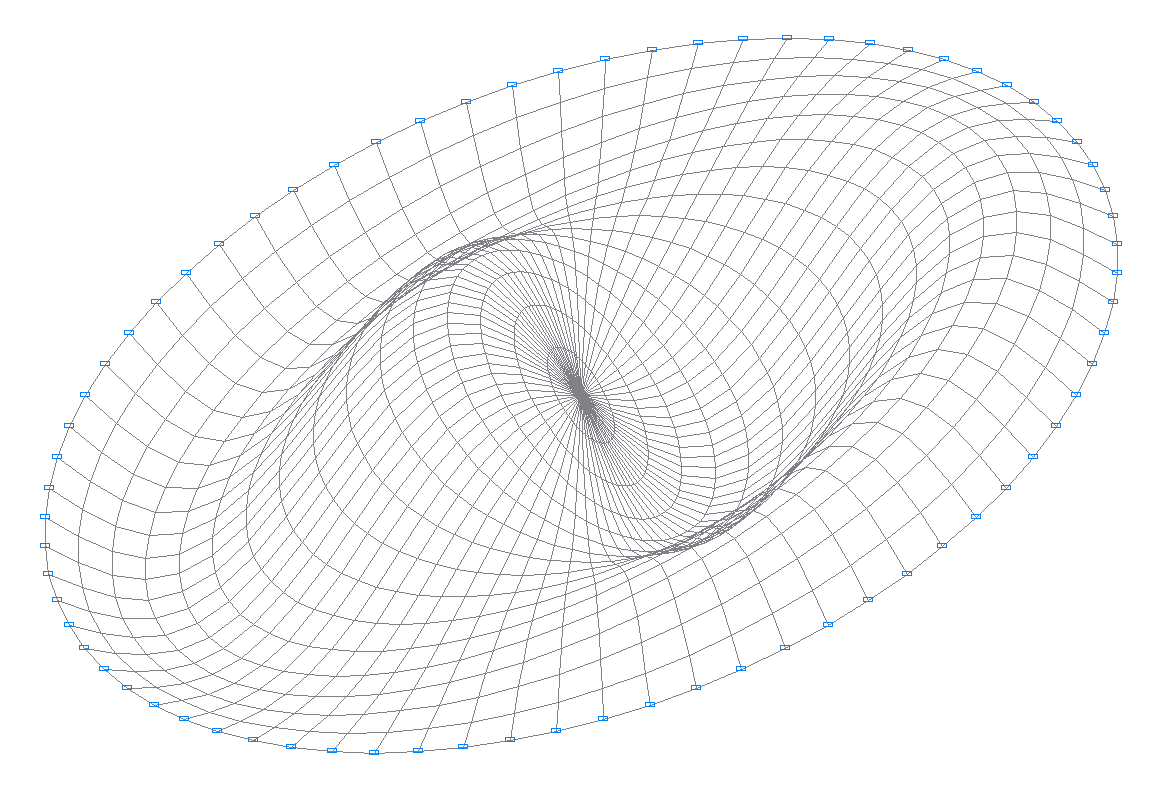

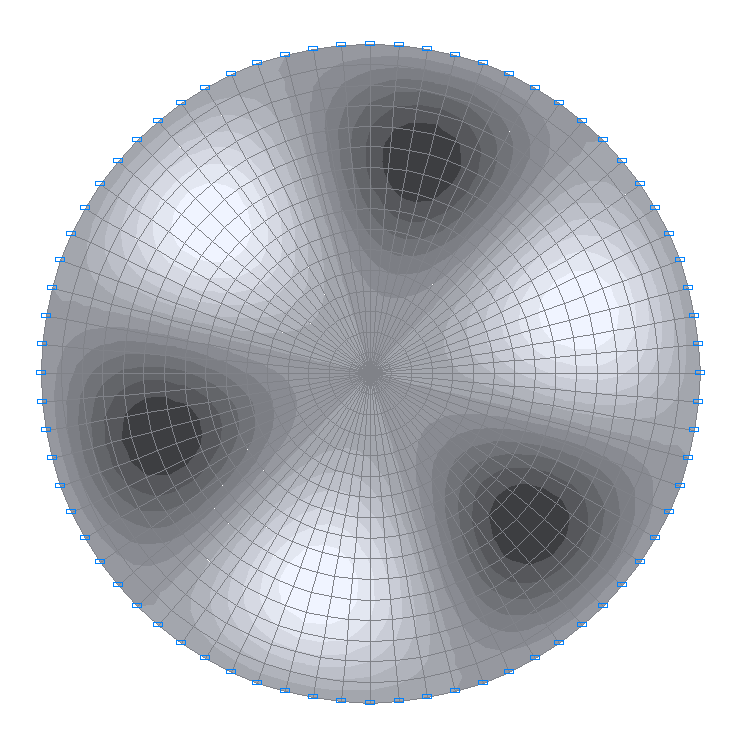
9-я собственная форма колебаний
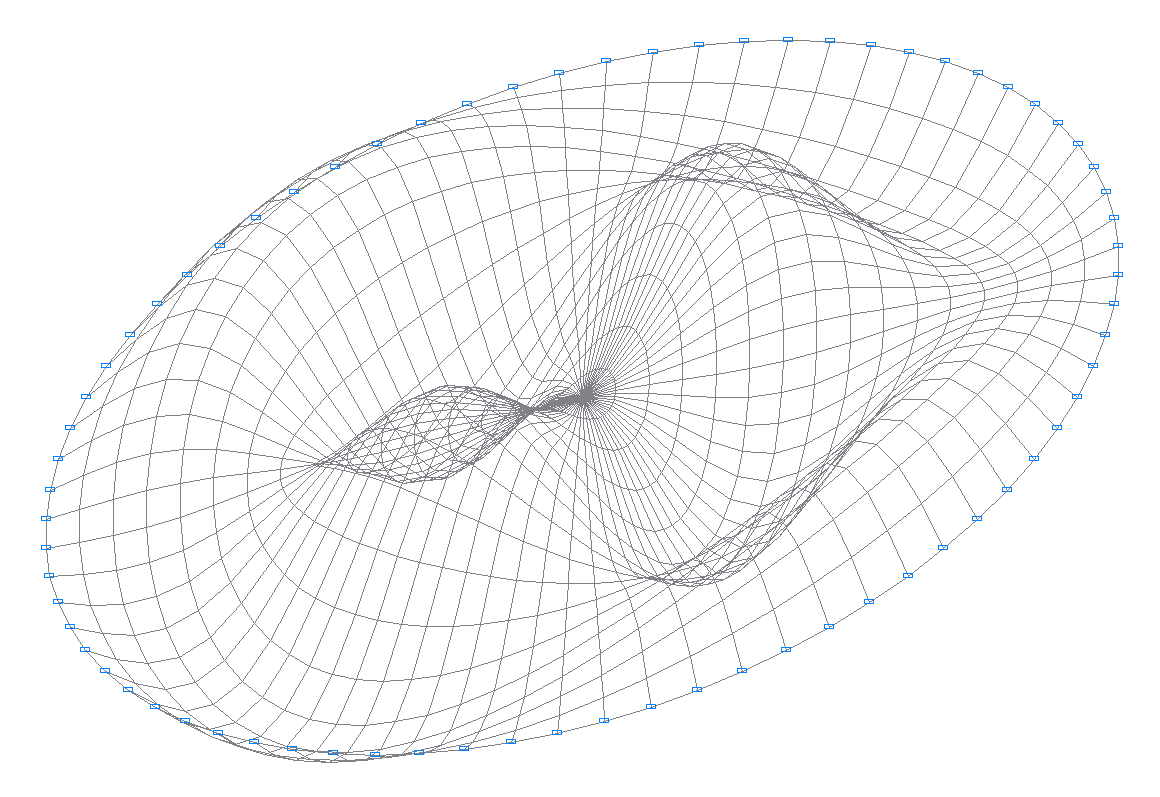
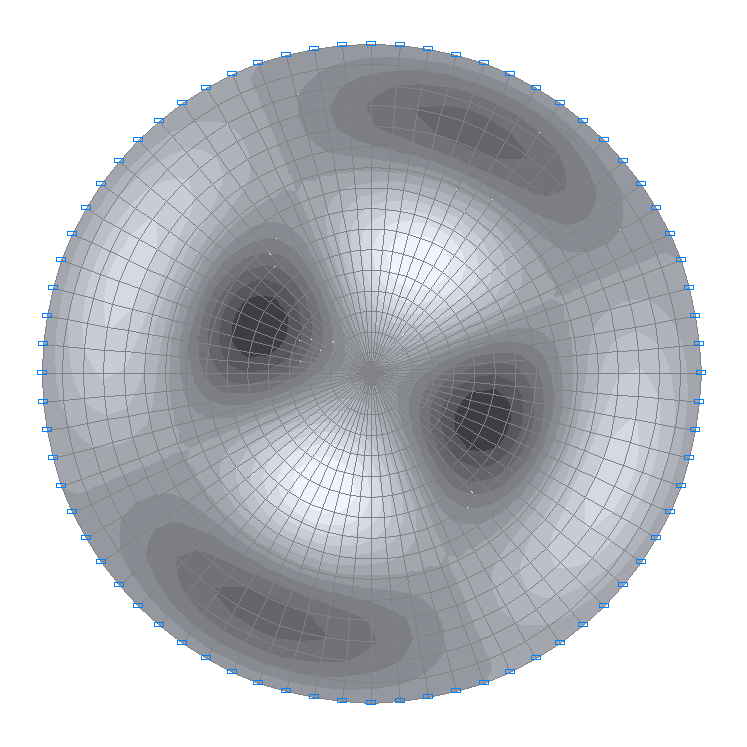

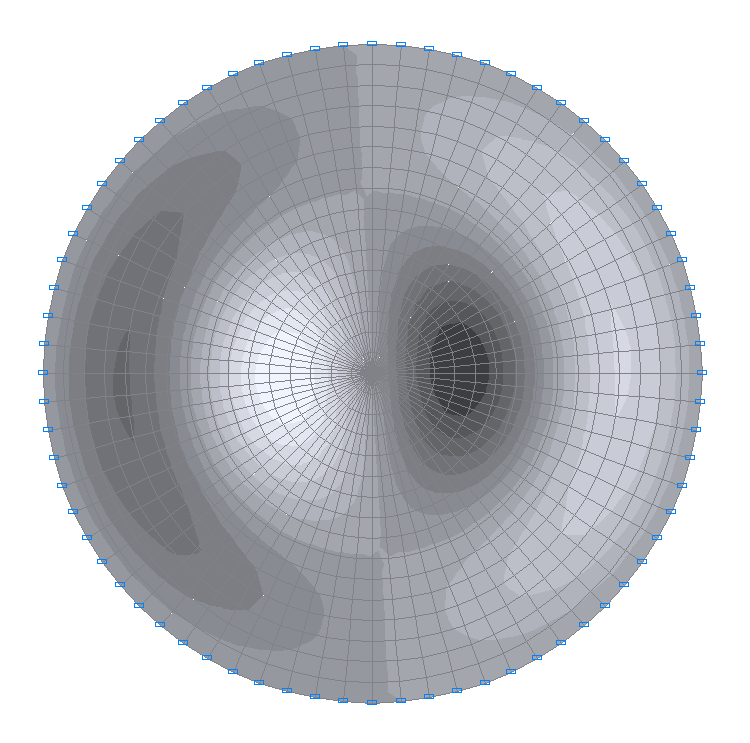
13-я собственная форма колебаний
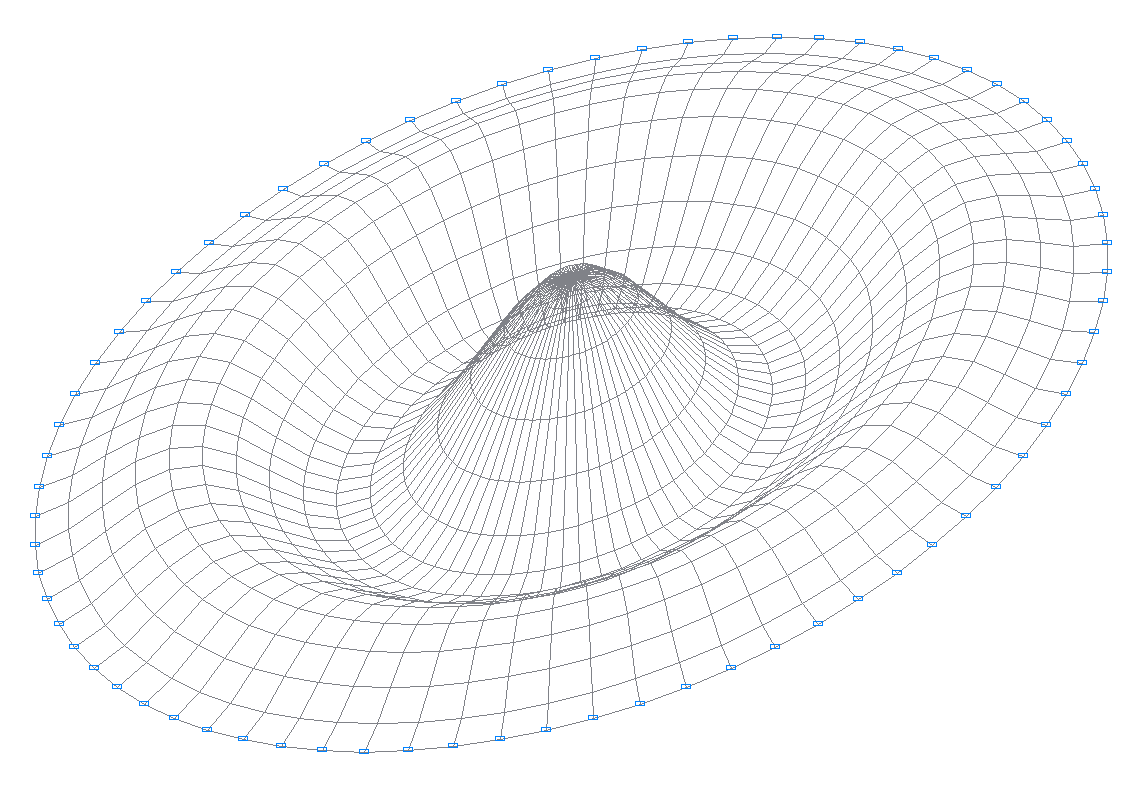


15-я собственная форма колебаний
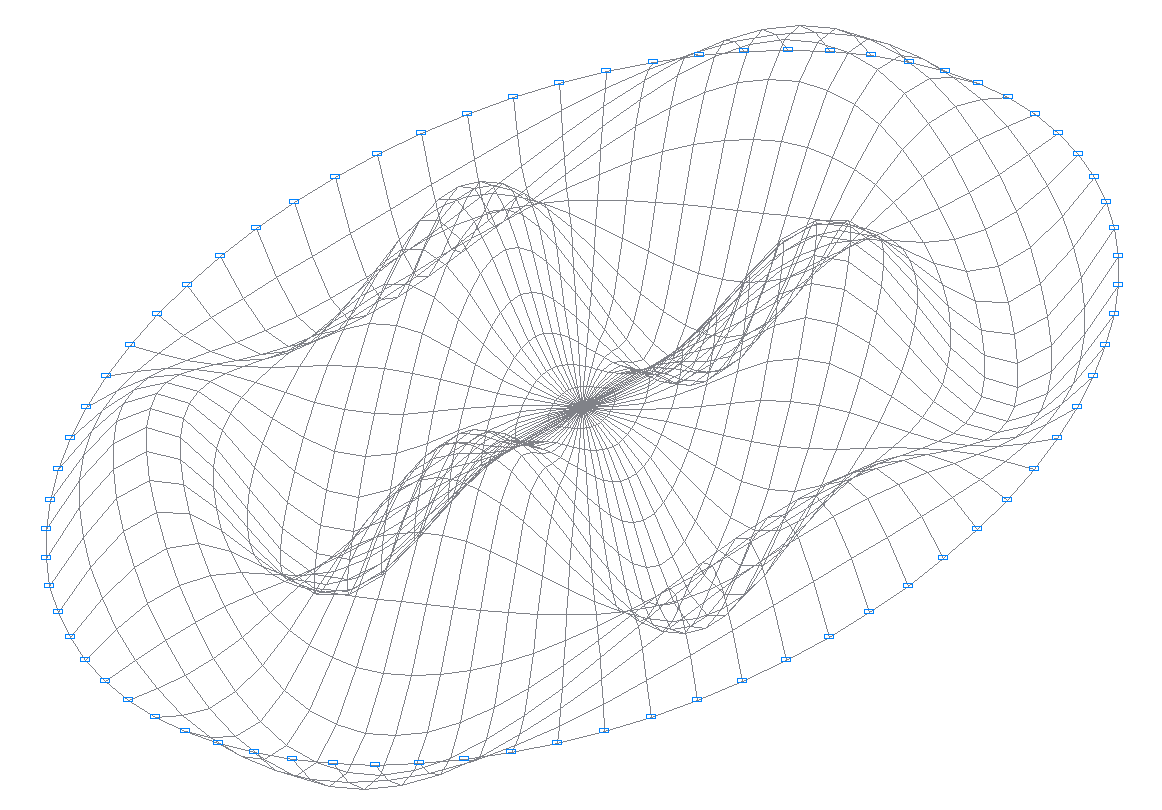
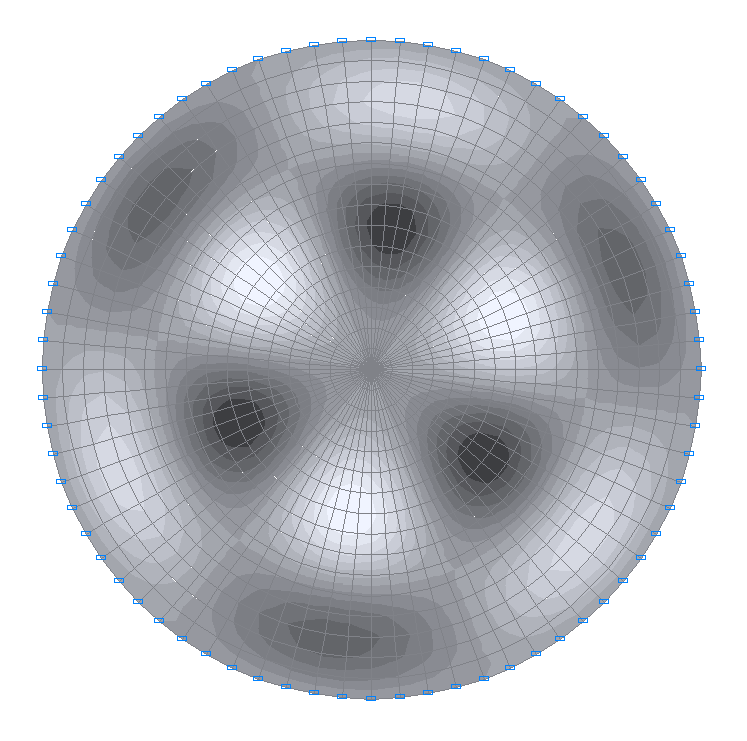

18-я собственная форма колебаний
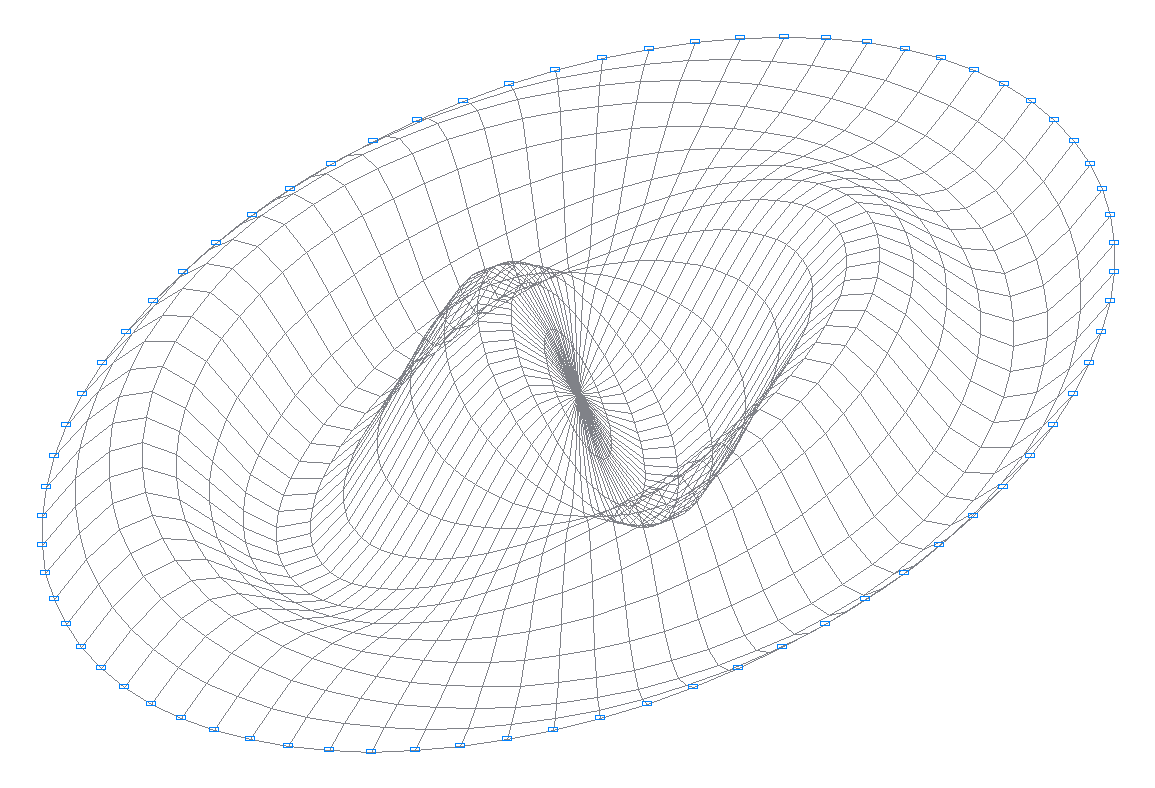
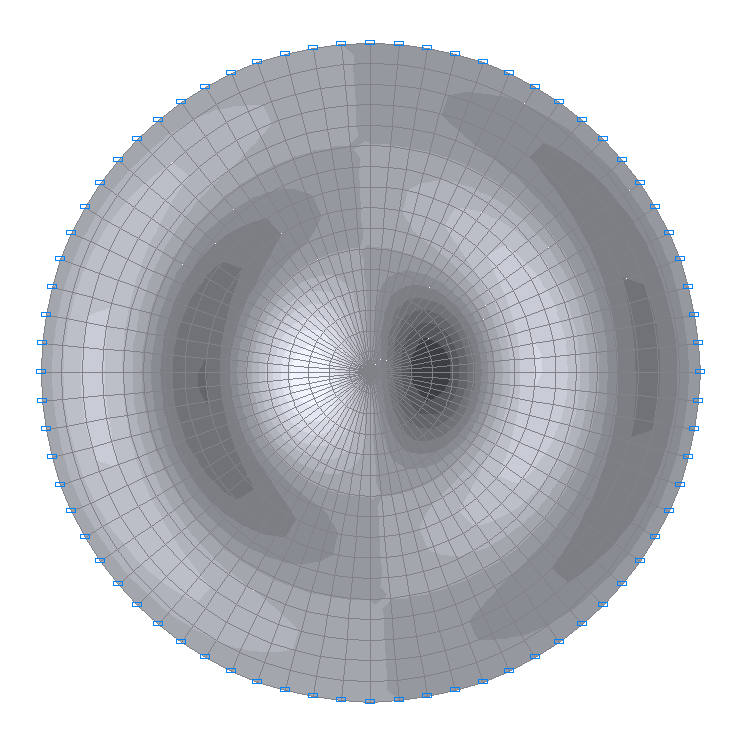

22-я собственная форма колебаний
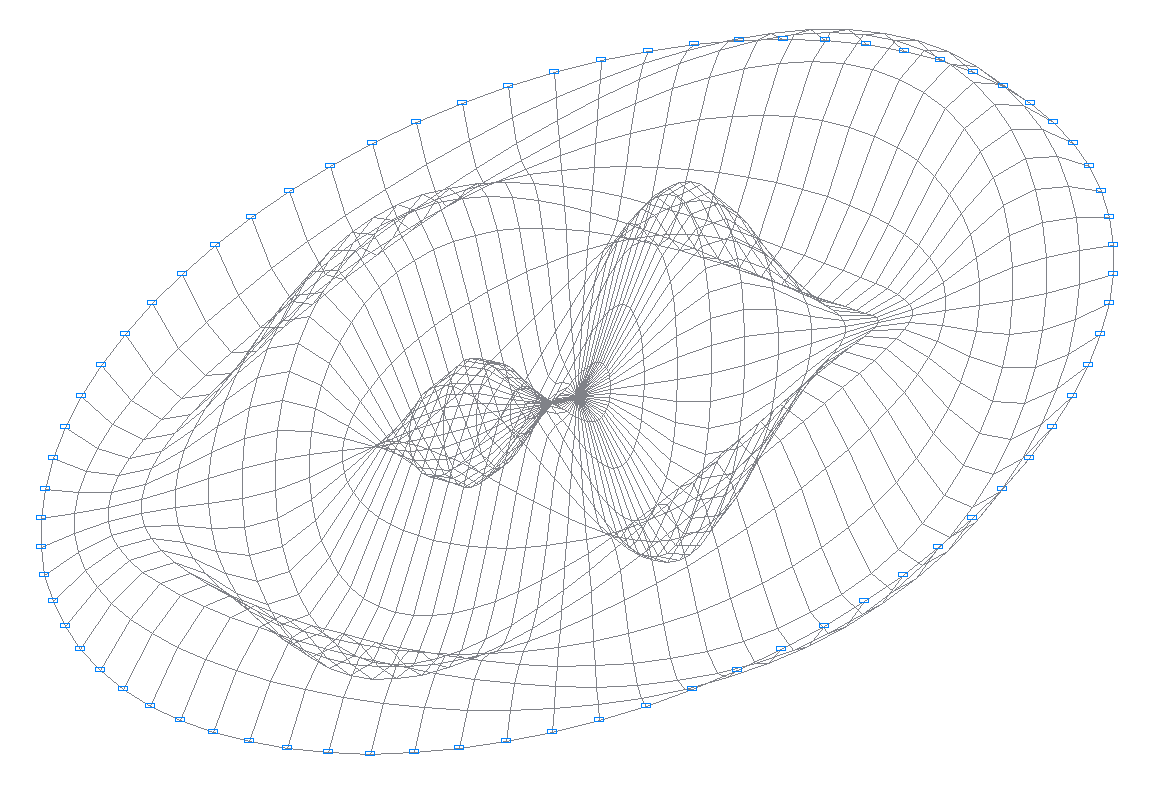


28-я собственная форма колебаний
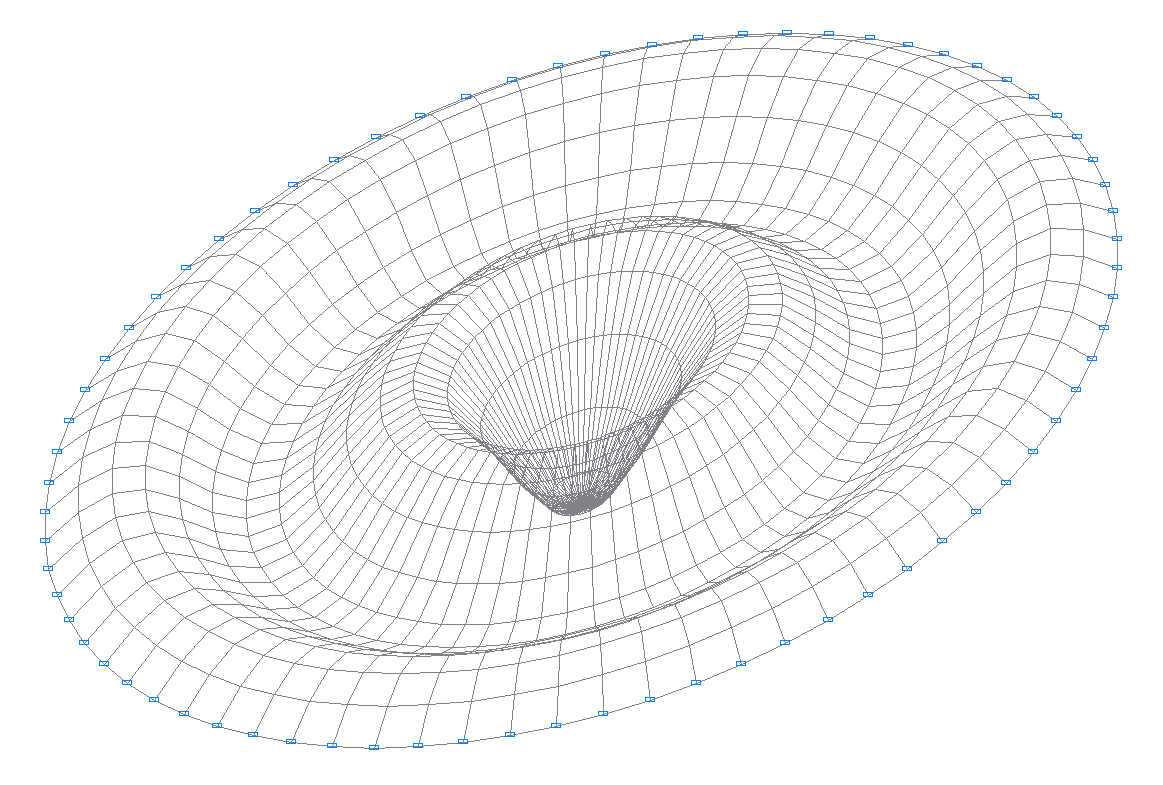
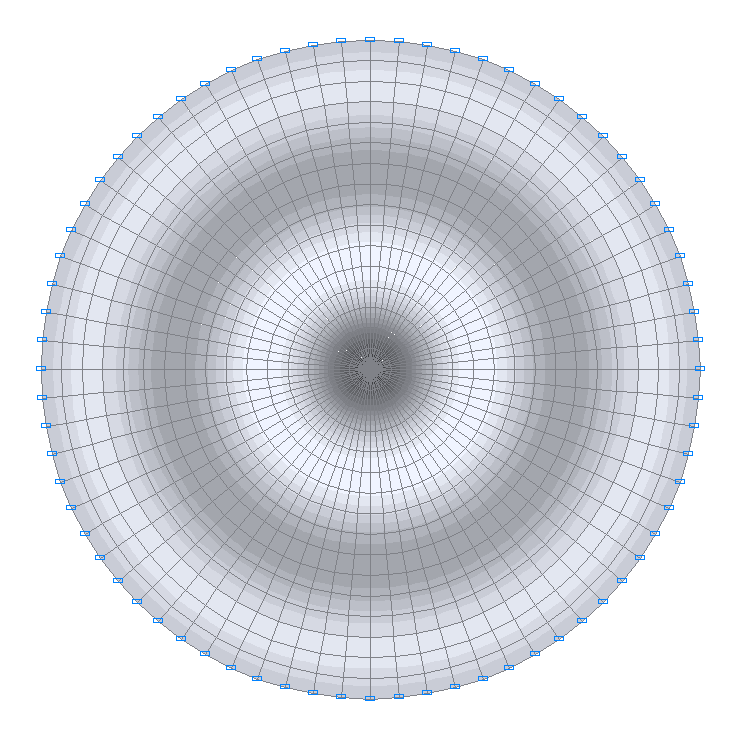

30-я собственная форма колебаний

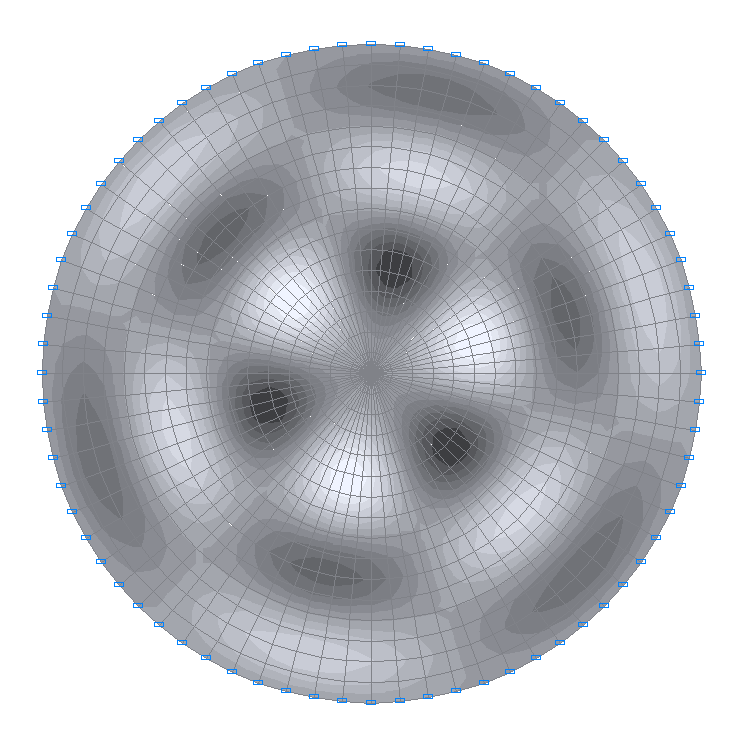

35-я собственная форма колебаний

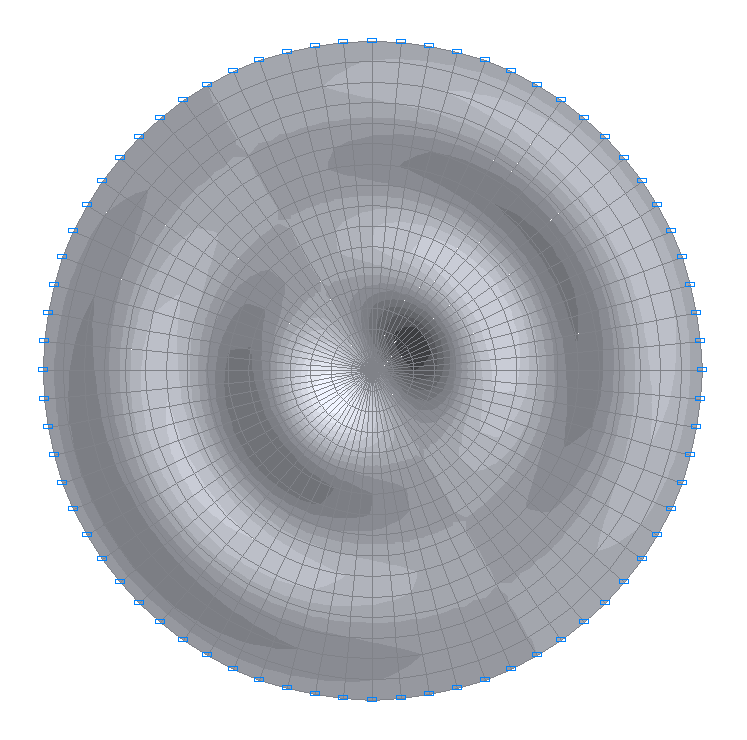

37-я собственная форма колебаний
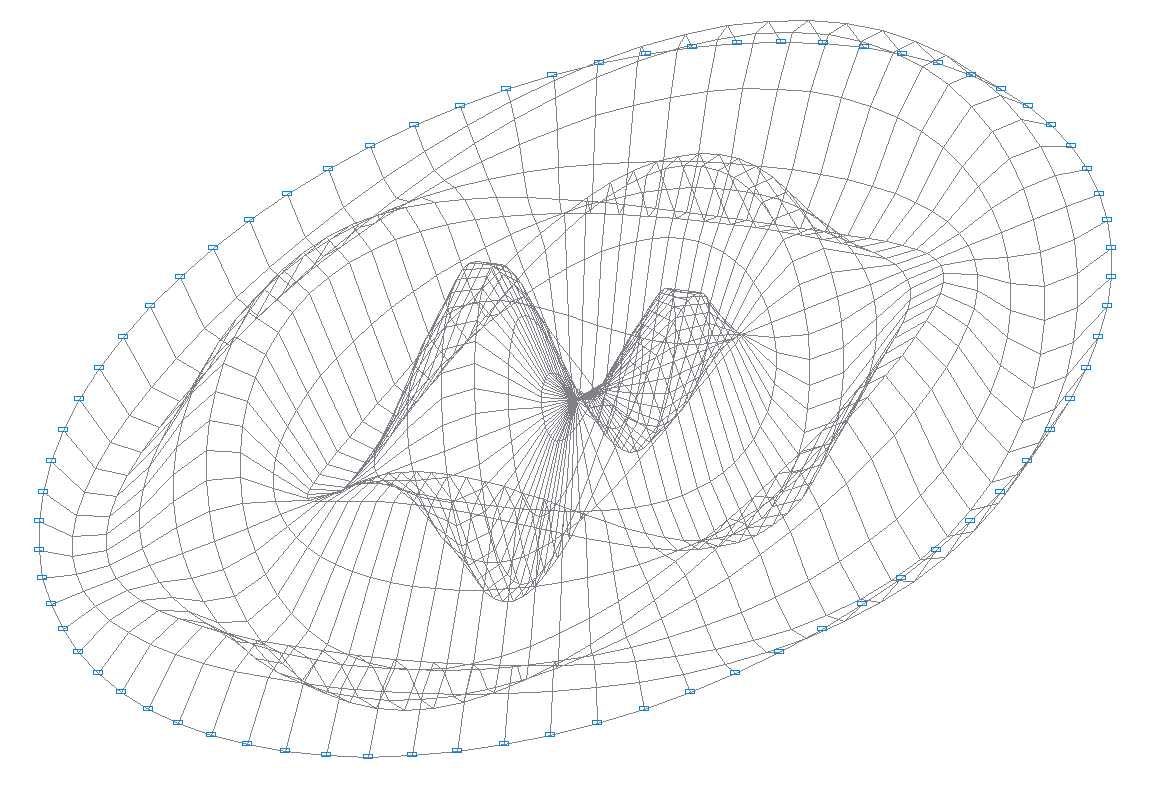
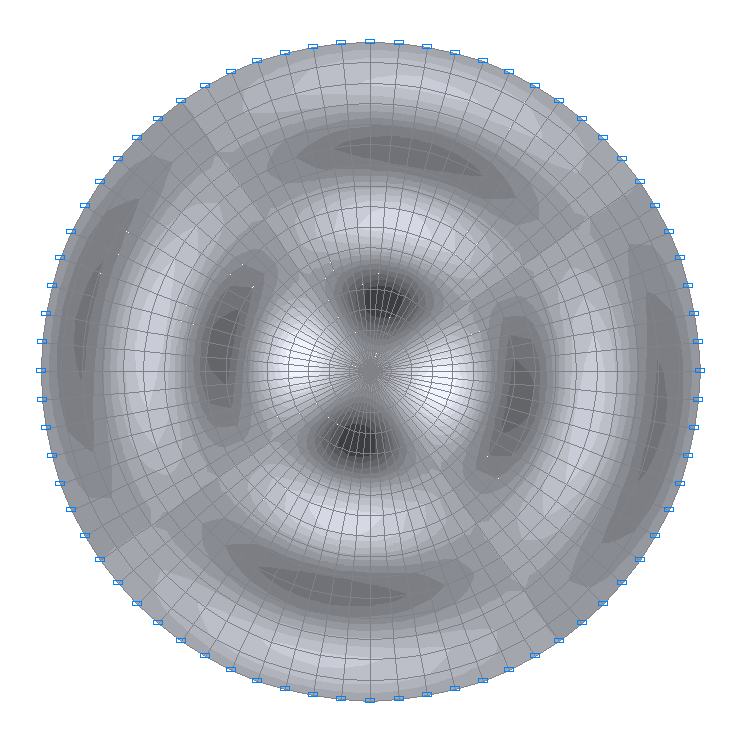

50-я (47-я теоретическая) собственная форма колебаний
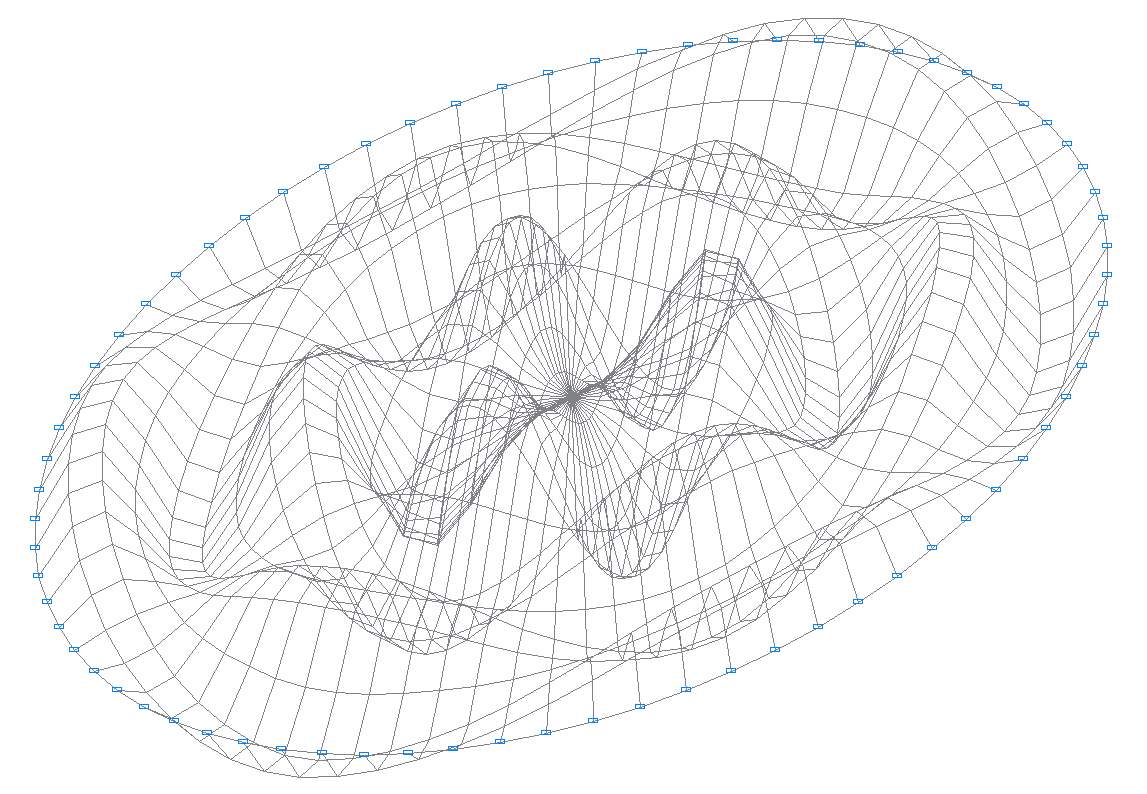


58-я собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, рад / с
|
Форма колебаний |
Число узловых окружностей m и диаметров n |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1 |
0, 0 |
306.0 |
305.8 |
0.07 |
|
2, 3 |
0, 1 |
861.8 |
862.4 |
0.07 |
|
4, 5 |
0, 2 |
1588.2 |
1590.5 |
0.14 |
|
6 |
1, 0 |
1842.9 |
1839.3 |
0.20 |
|
7, 8 |
0, 3 |
2477.7 |
2483.2 |
0.22 |
|
9, 10 |
1, 1 |
3006.1 |
3011.2 |
0.17 |
|
11, 12 |
0, 4 |
3524.6 |
3532.7 |
0.23 |
|
13, 14 |
1, 2 |
4347.8 |
4366.4 |
0.43 |
|
15 |
2, 0 |
4598.3 |
4582.6 |
0.34 |
|
16, 17 |
0, 5 |
4725.2 |
4738.1 |
0.27 |
|
18, 19 |
1, 3 |
5862.8 |
5890.3 |
0.47 |
|
20, 21 |
0, 6 |
6076.4 |
6097.0 |
0.34 |
|
22, 23 |
2, 1 |
6372.8 |
6390.0 |
0.27 |
|
24, 25 |
0, 7 |
7546.5 |
7581.9 |
0.47 |
|
26, 27 |
1, 4 |
7576.1 |
7607.4 |
0.41 |
|
28, 29 |
2, 2 |
8327.5 |
8402.9 |
0.91 |
|
30 |
3, 0 |
8576.8 |
8534.9 |
0.49 |
|
31, 32 |
0, 8 |
9222.3 |
9267.5 |
0.49 |
|
33, 34 |
1, 5 |
9395.3 |
9441.9 |
0.50 |
|
35, 36 |
2, 3 |
10459.2 |
10539.6 |
0.77 |
|
37, 38 |
0, 9 |
10963.1 |
11004.7 |
0.38 |
|
39, 40 |
3, 1 |
11013.5 |
11076.0 |
0.57 |
|
41, 42 |
1, 6 |
11406.2 |
11471.2 |
0.57 |
|
43, 44 |
2, 4 |
12764.4 |
12865.5 |
0.79 |
|
45, 46 |
0, 10 |
12948.4 |
13031.2 |
0.64 |
|
47, 48 |
3, 2 |
13530.3 |
13742.7 |
1.57 |
|
49, 50 |
1, 7 |
13576.7 |
13667.2 |
0.67 |
|
51 |
4, 0 |
13779.1 |
13690.3 |
0.64 |
|
52, 53 |
0, 11 |
15025.9 |
15131.7 |
0.70 |
|
54, 55 |
2, 5 |
15240.2 |
15359.6 |
0.78 |
|
56, 57 |
1, 8 |
15904.6 |
16028.2 |
0.78 |
|
58, 59 |
3, 3 |
16276.1 |
16457.3 |
1.11 |
|
60, 61 |
4, 1 |
16777.2 |
16859.0 |
0.49 |
Замечания: При аналитическом решении собственные частоты колебаний ω круговой квадратной шарнирно опертой по контуру пластины с плотностью материала ρ могут быть определены из следующего уравнения, полученного на основе метода факторизации:
\[\frac{J_{n+1} \left( {\beta \cdot R} \right)}{J_{n} \left( {\beta \cdot R} \right)}+\frac{I_{n+1} \left( {\beta \cdot R} \right)}{I_{n} \left( {\beta \cdot R} \right)}=\frac{2\cdot \beta \cdot R}{1-\nu },\quad \]
где: \( \beta =\left( {\frac{\rho \cdot h\cdot \omega^{2}}{D}} \right)^{\frac{1}{4}}, \quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \) n=0,1,2,3, - число узловых диаметров,
\( J_{n} \left( {\beta \cdot R} \right), \quad J_{n+1} \left( {\beta \cdot R} \right) \) - значения функции Бесселя первого рода n-го порядка
\( I_{n} \left( {\beta \cdot R} \right), \quad I_{n+1} \left( {\beta \cdot R} \right) \) - значения модифицированной функции Бесселя первого рода n-го порядка.
