Свободные колебания круговой жестко защемленной по контуру пластины
Цель: Модальный анализ круговой жестко защемленной по контуру пластины.
Файл с исходными данными: 5.6.spr
Формулировка задачи: Определить собственные формы и частоты колебаний ω круговой жестко защемленной по контуру пластины с плотностью материала ρ.
Ссылки: В. Н. Челомей, Вибрации в технике, Справочник в шести томах: В. В. Болотин, Том 1, Колебания линейных систем, Москва, Машиностроение, 1978, стр. 207.
Исходные данные:
| E = 2.06·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 7.85 т/м3 | - плотность материала; |
| h = 0.01 м | - толщина пластины; |
| R = 0.5 м | - наружный радиус пластины. |
Конечноэлементная модель: Расчетная схема – балочный ростверк / плита, 1080 четырехузловых элементов плиты типа 20 и 72 трехузловых элемента плиты типа 15. Сетка конечных элементов разбита с шагом 0.03125 м в радиальном направлении и с шагом 5.0º в тангенциальном направлении. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы Z, UX, UY по наружному контуру пластины. Распределенная масса задается преобразованием статической нагрузки от собственного веса пластины ow = γ•h, где γ = ρ•g = 77.01 кН/м3. Количество узлов в расчетной схеме – 1153. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD
Расчетная схема
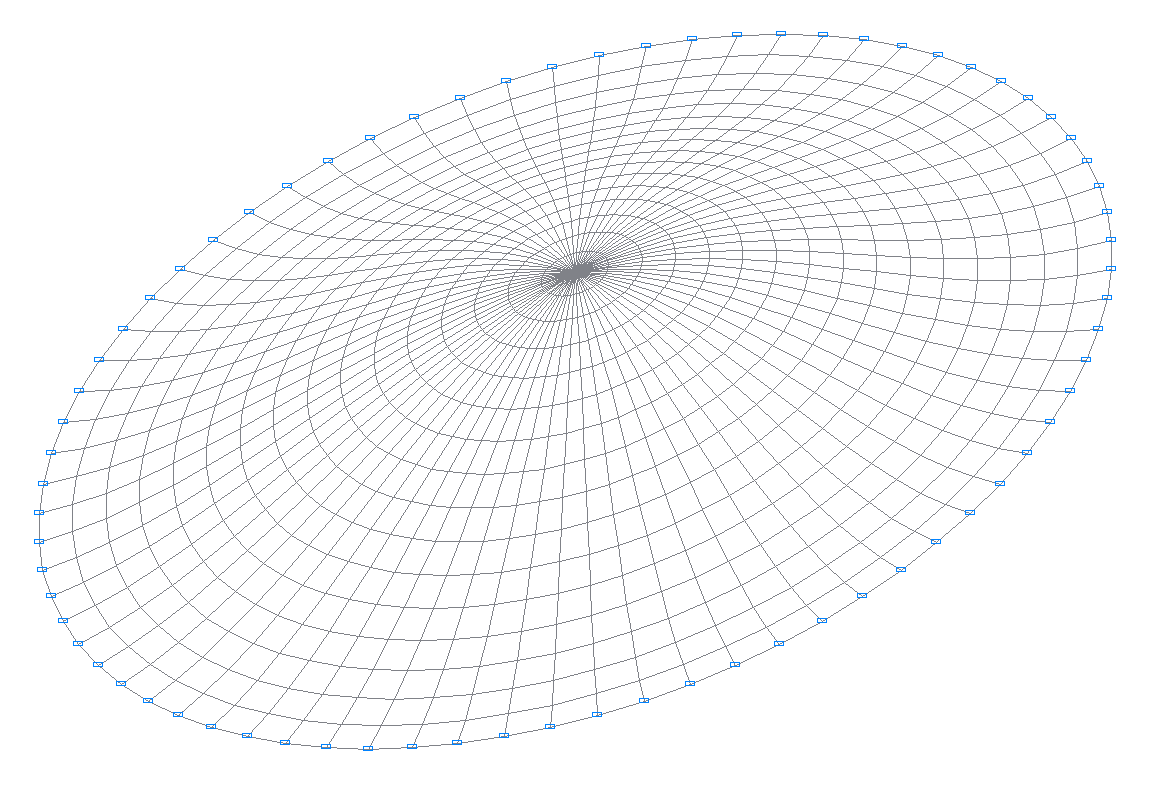
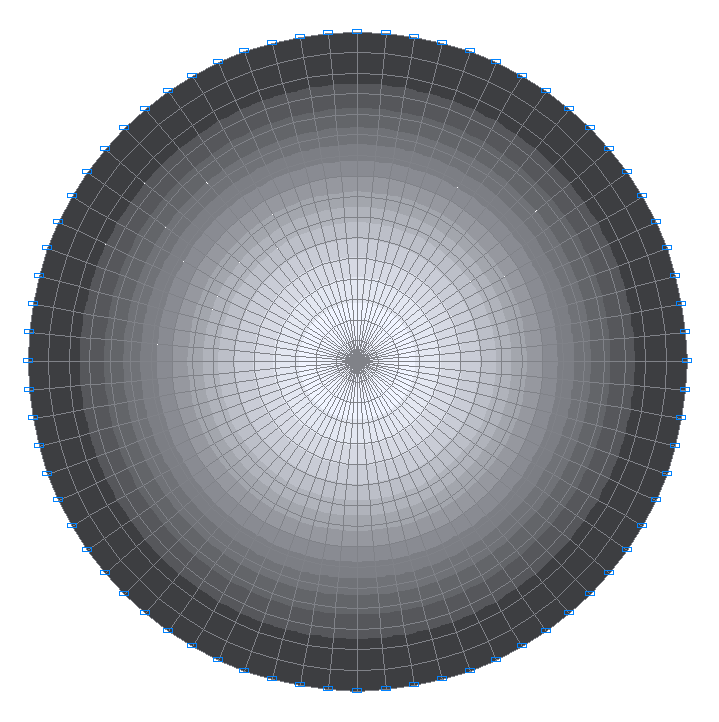

1-я собственная форма колебаний
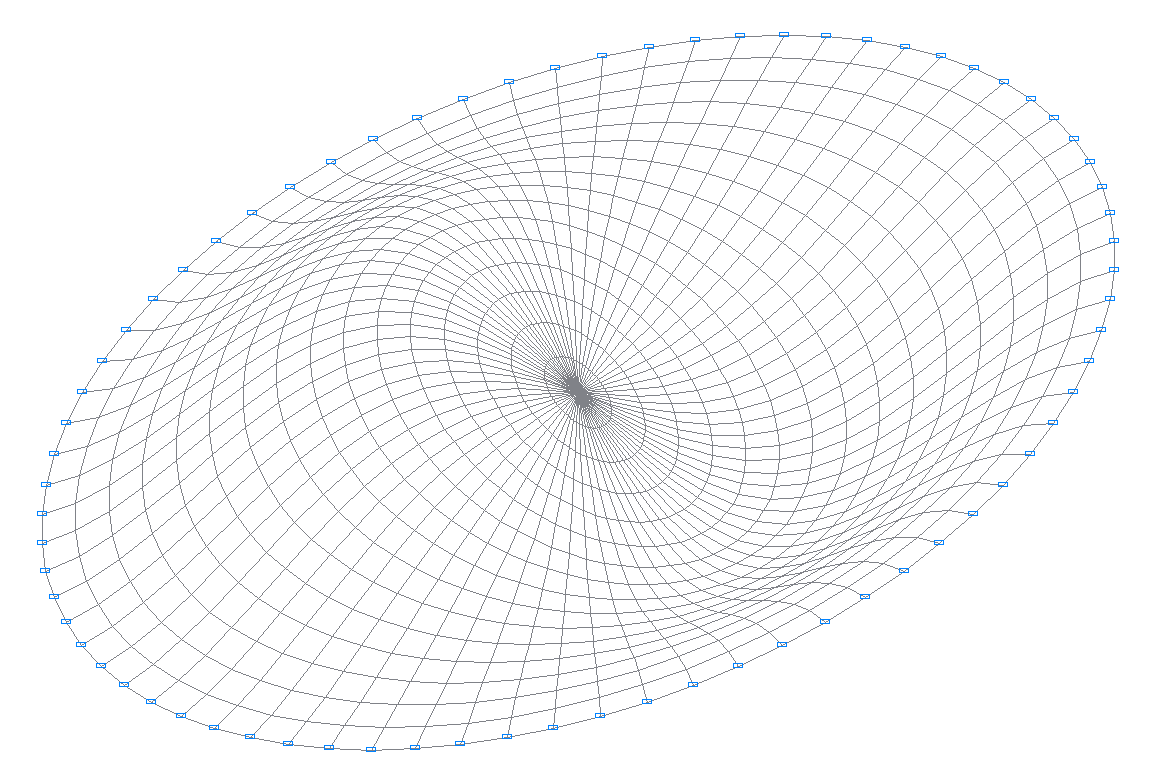
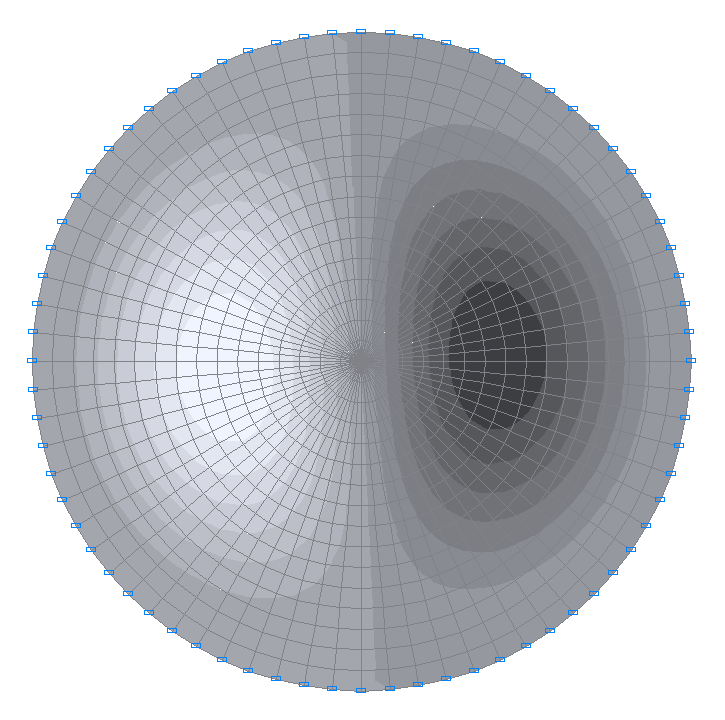

2-я собственная форма колебаний
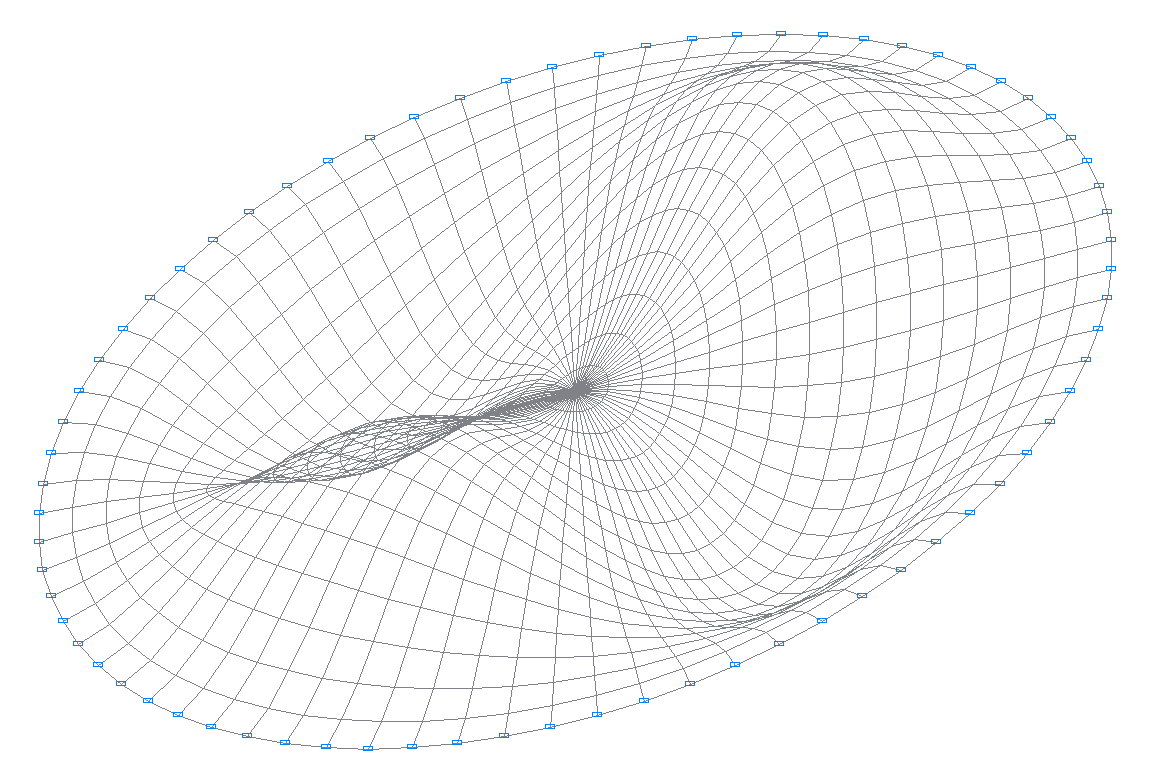
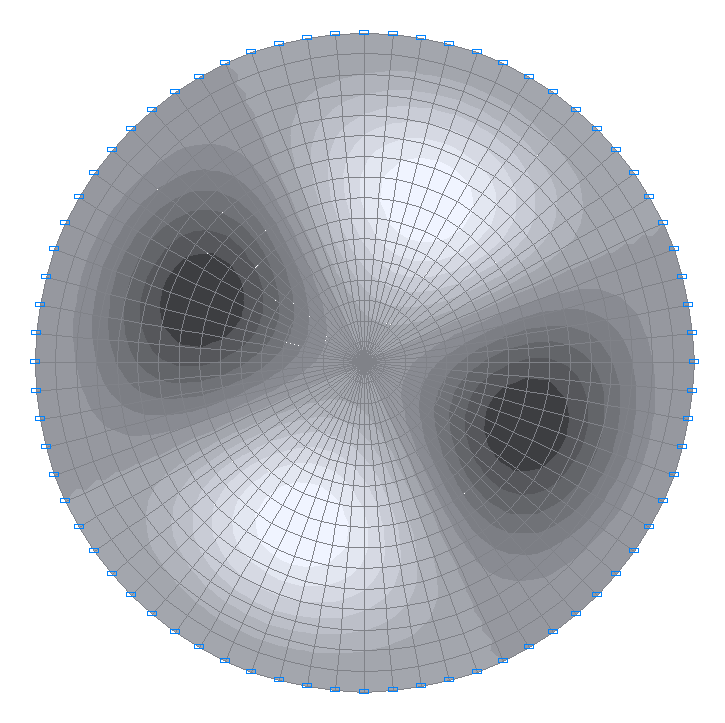

4-я собственная форма колебаний
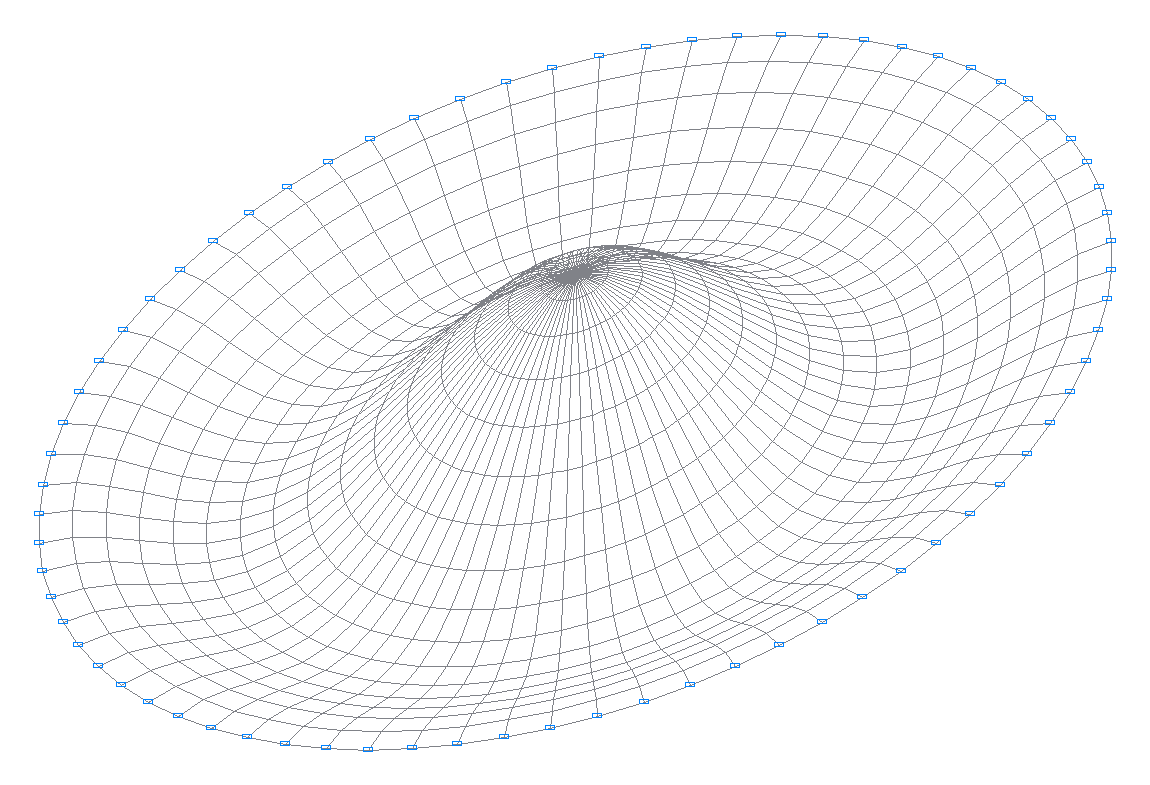
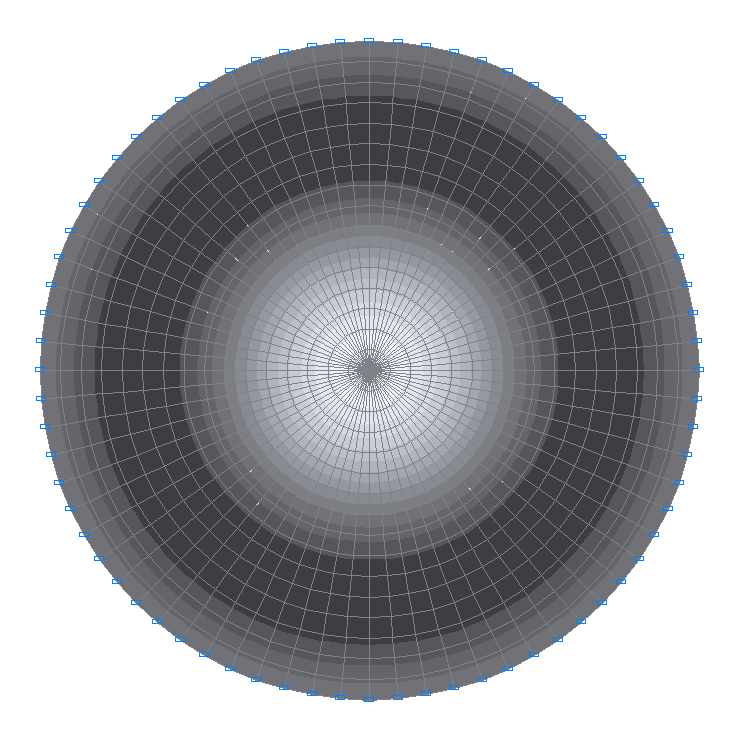

6-я собственная форма колебаний
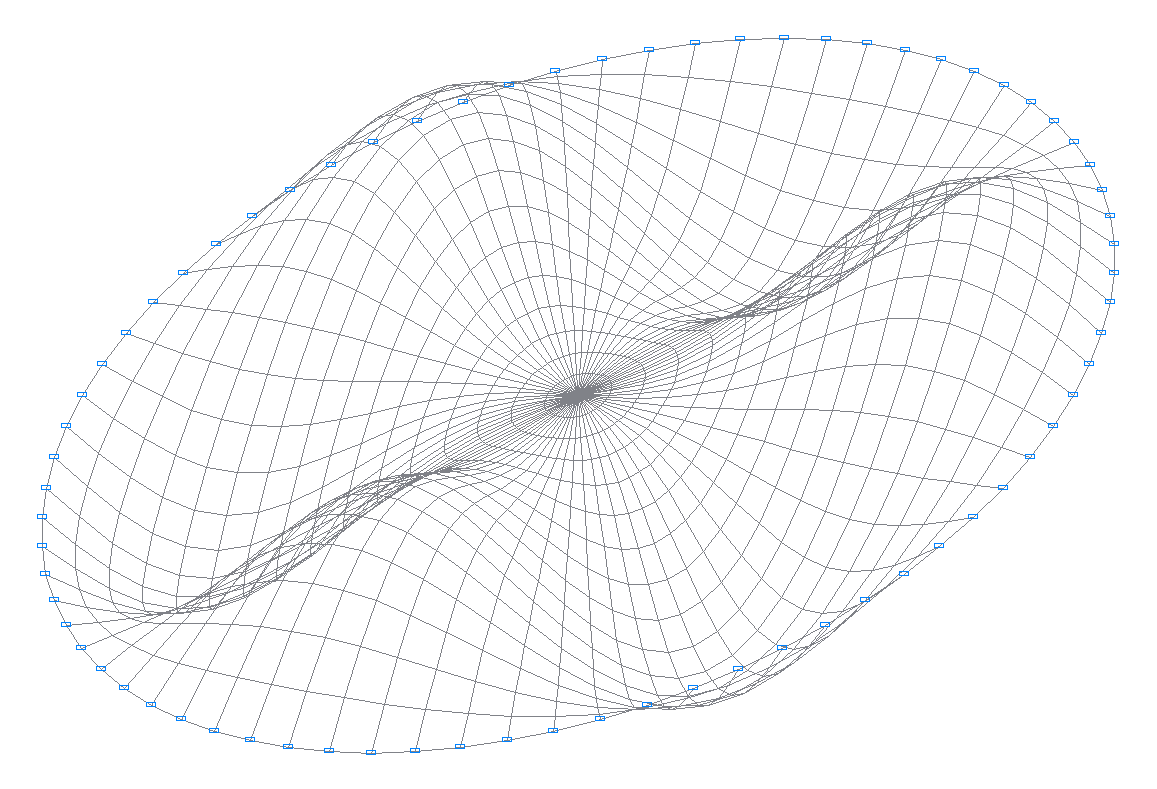
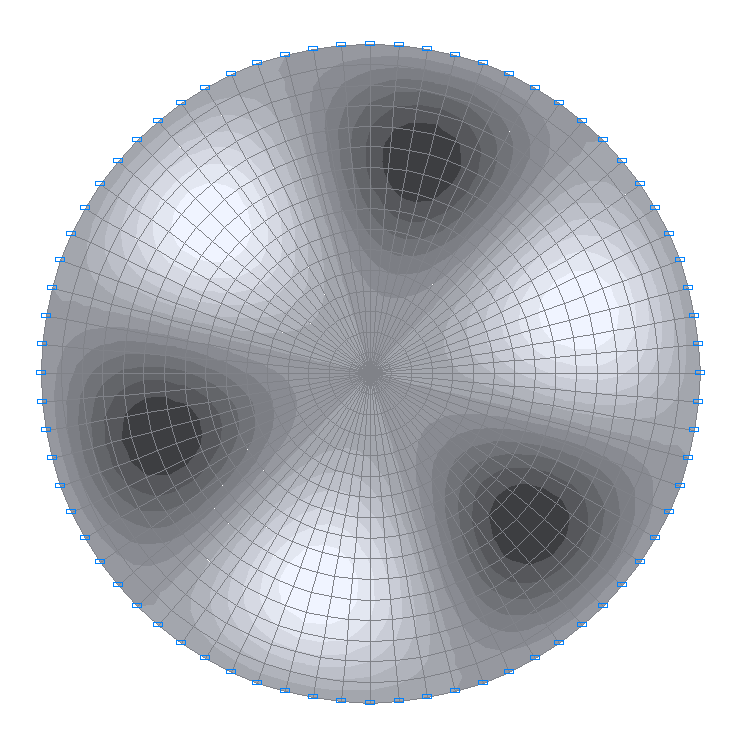

7-я собственная форма колебаний
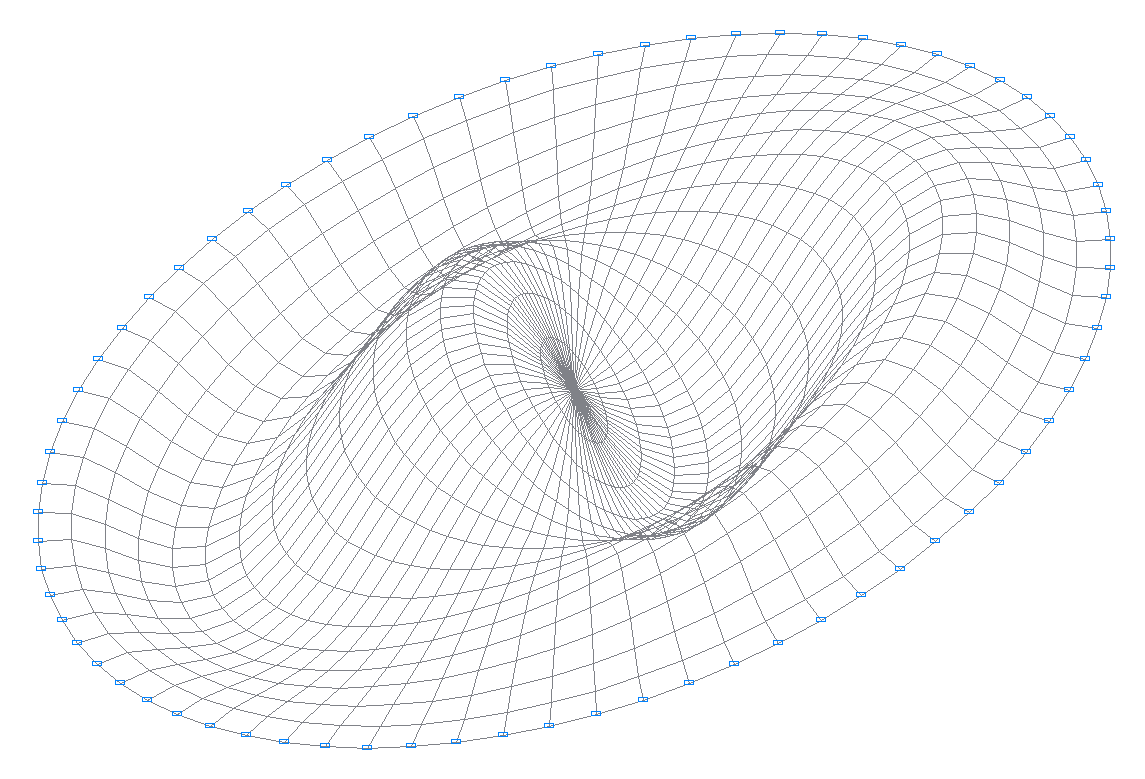
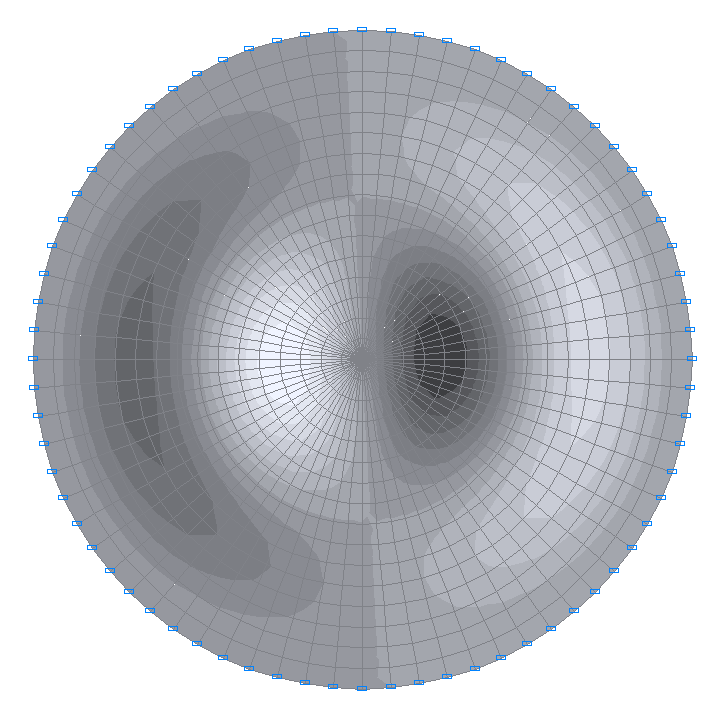

9-я собственная форма колебаний
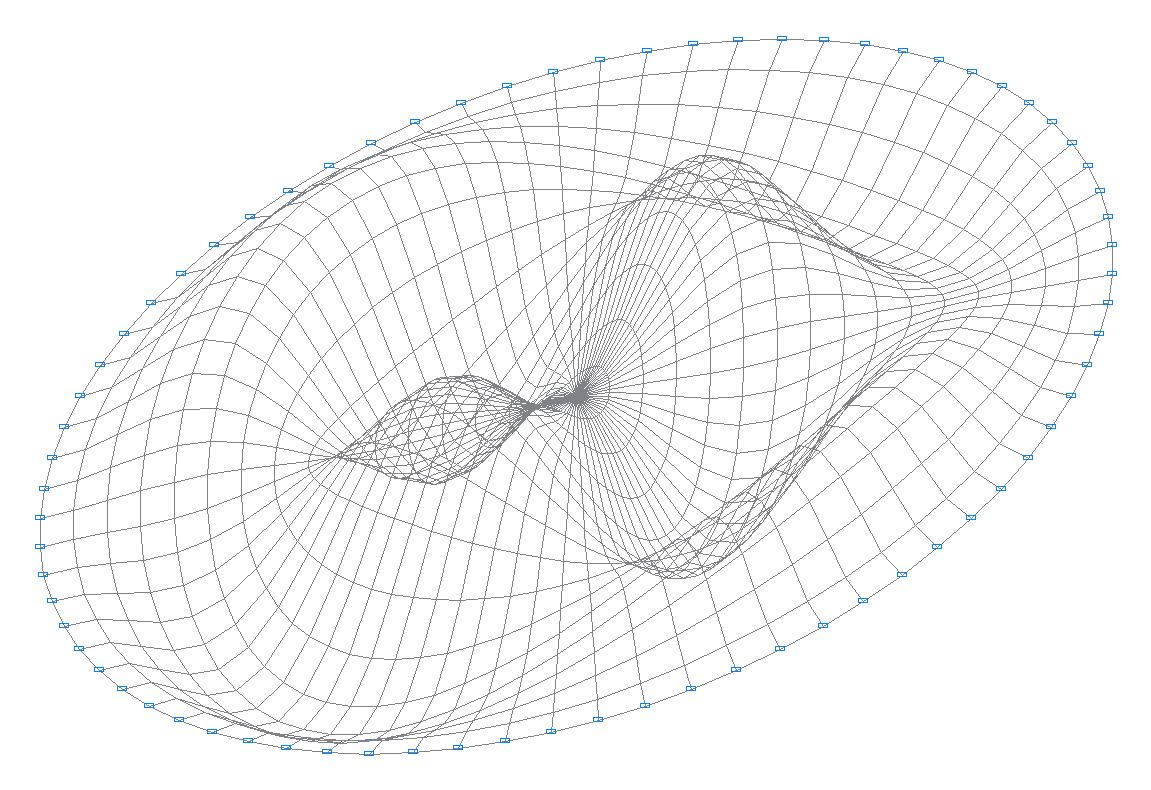
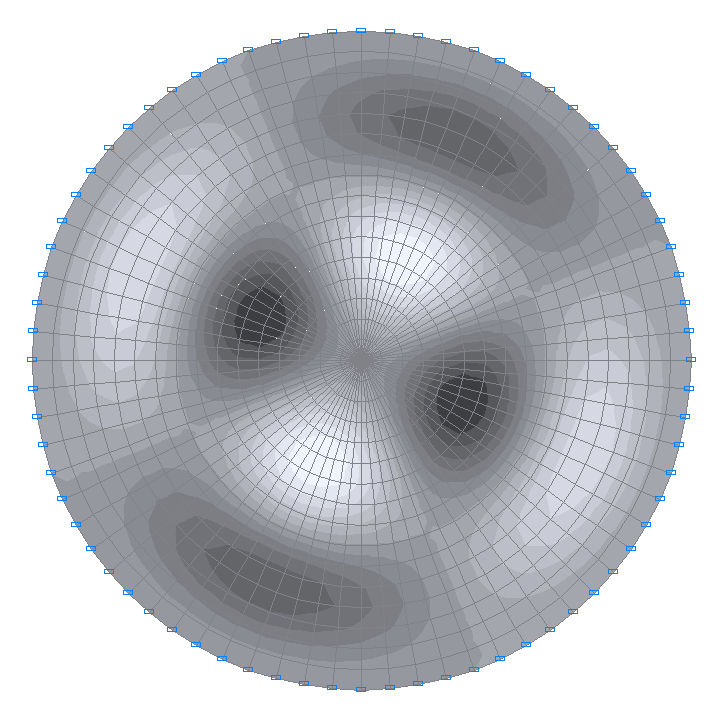

13-я собственная форма колебаний



15-я собственная форма колебаний
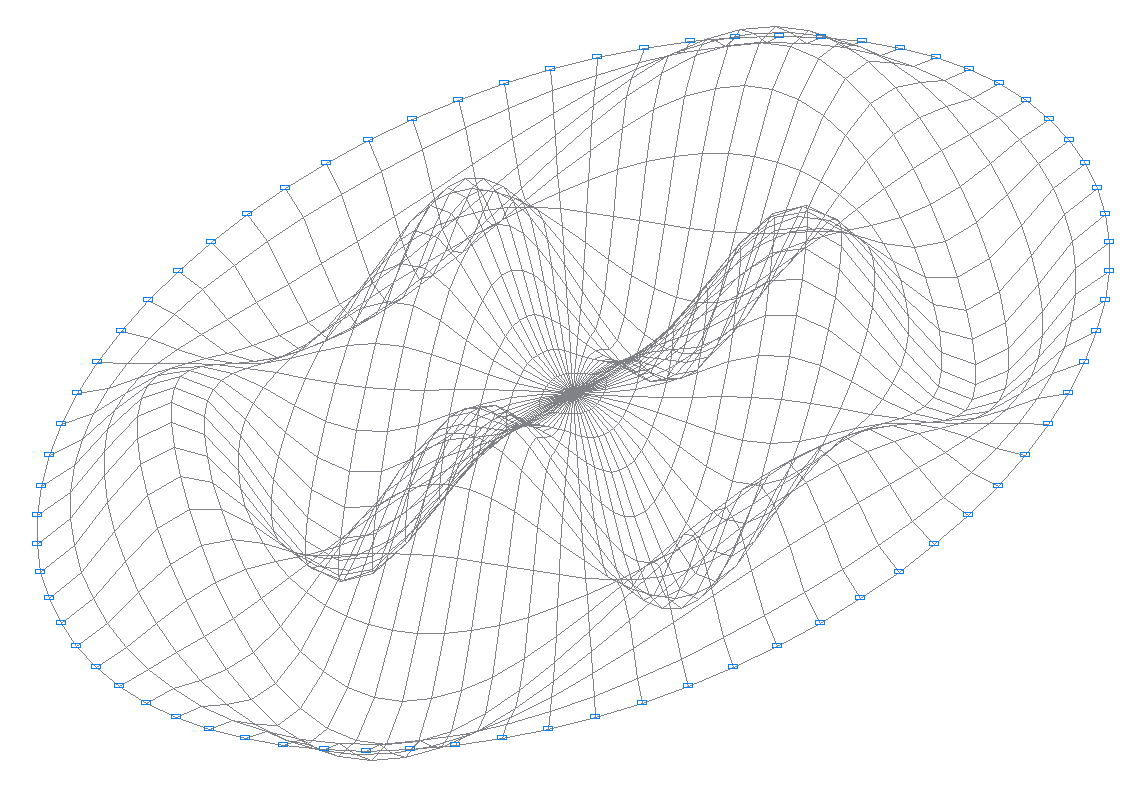


18-я собственная форма колебаний
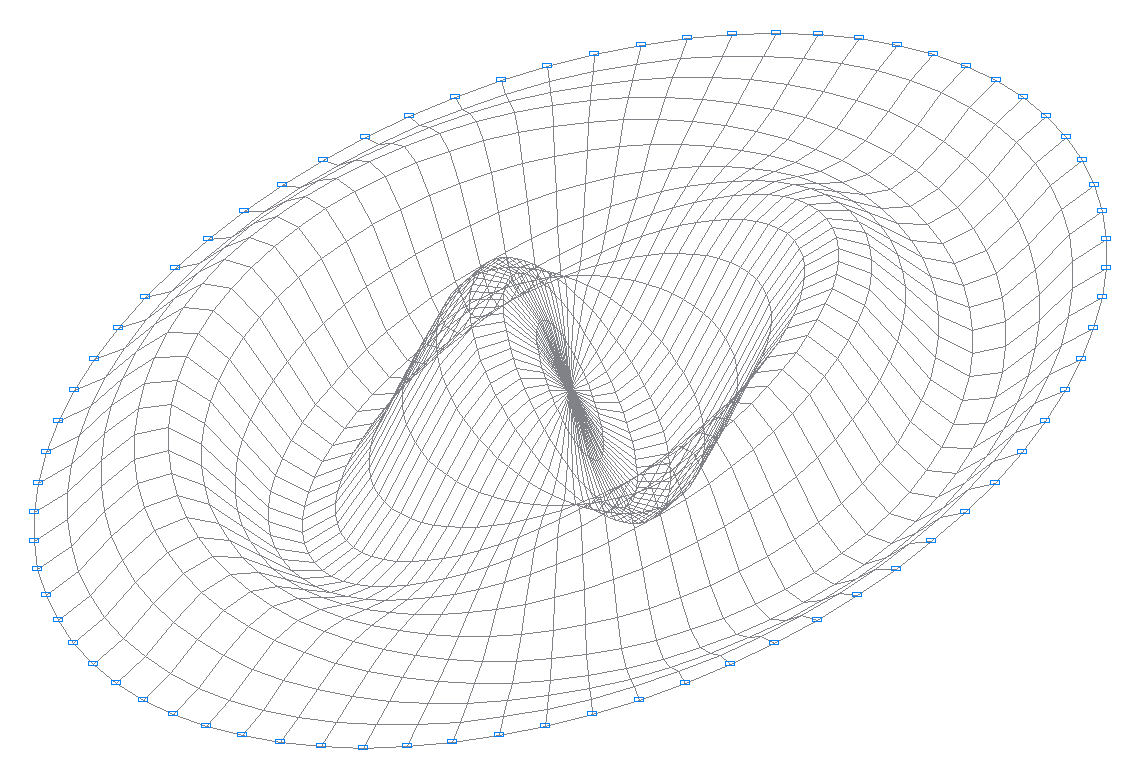
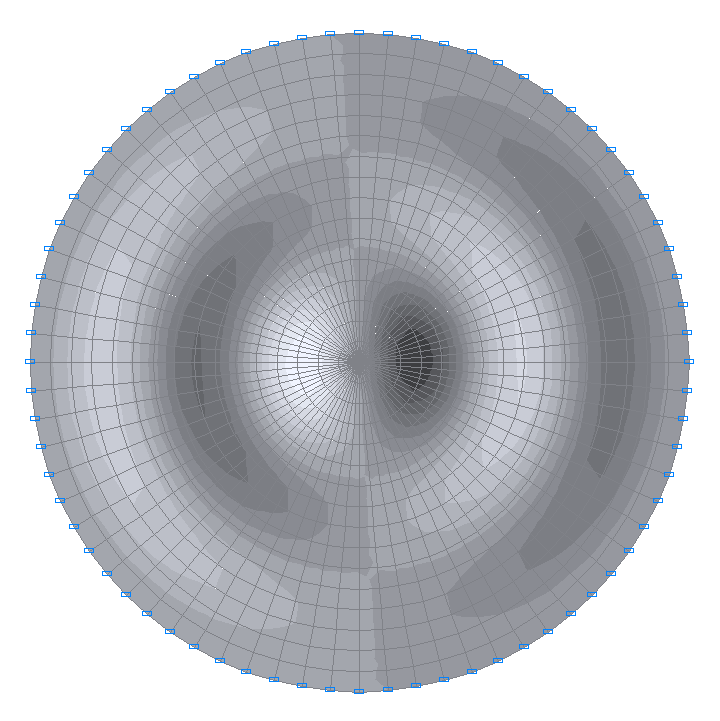

22-я собственная форма колебаний
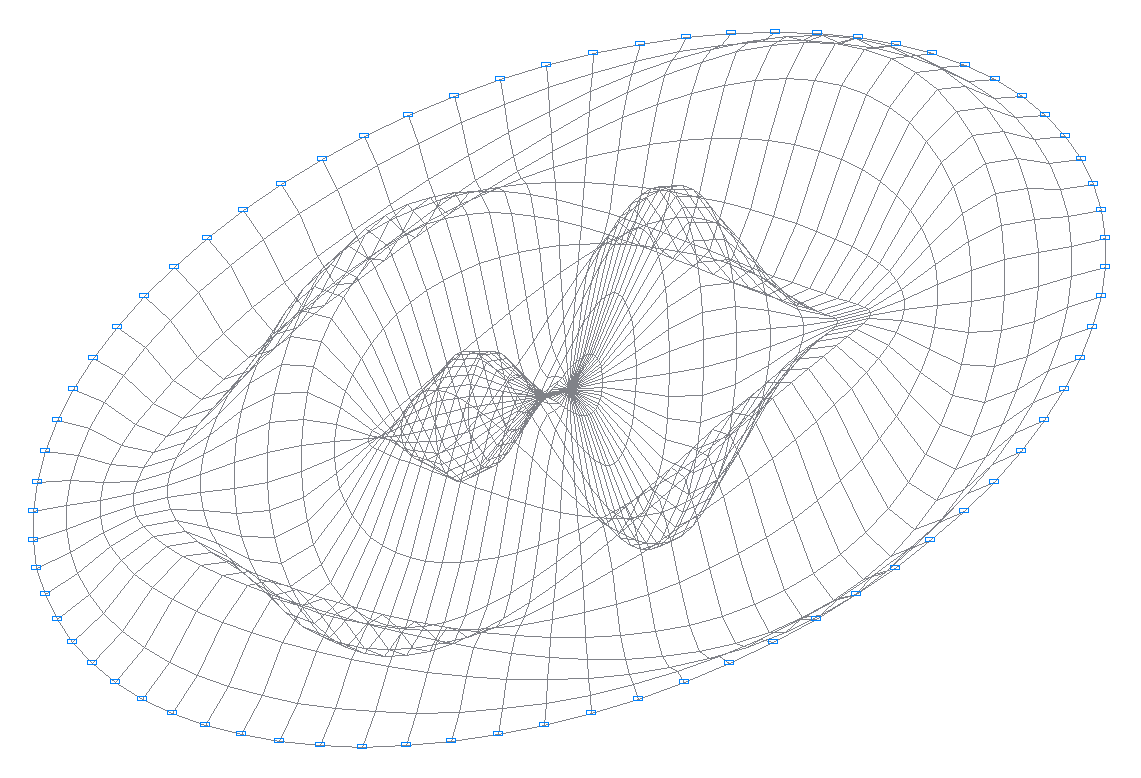
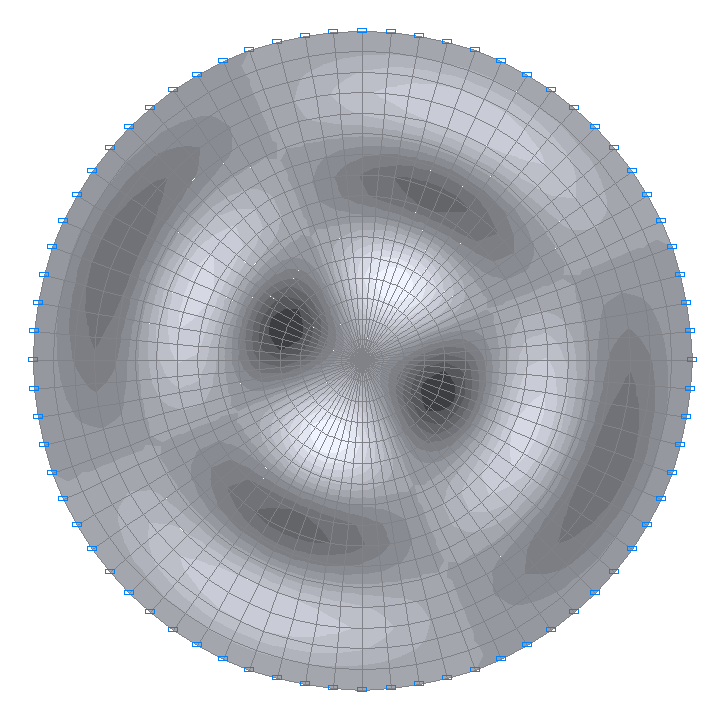

28-я собственная форма колебаний
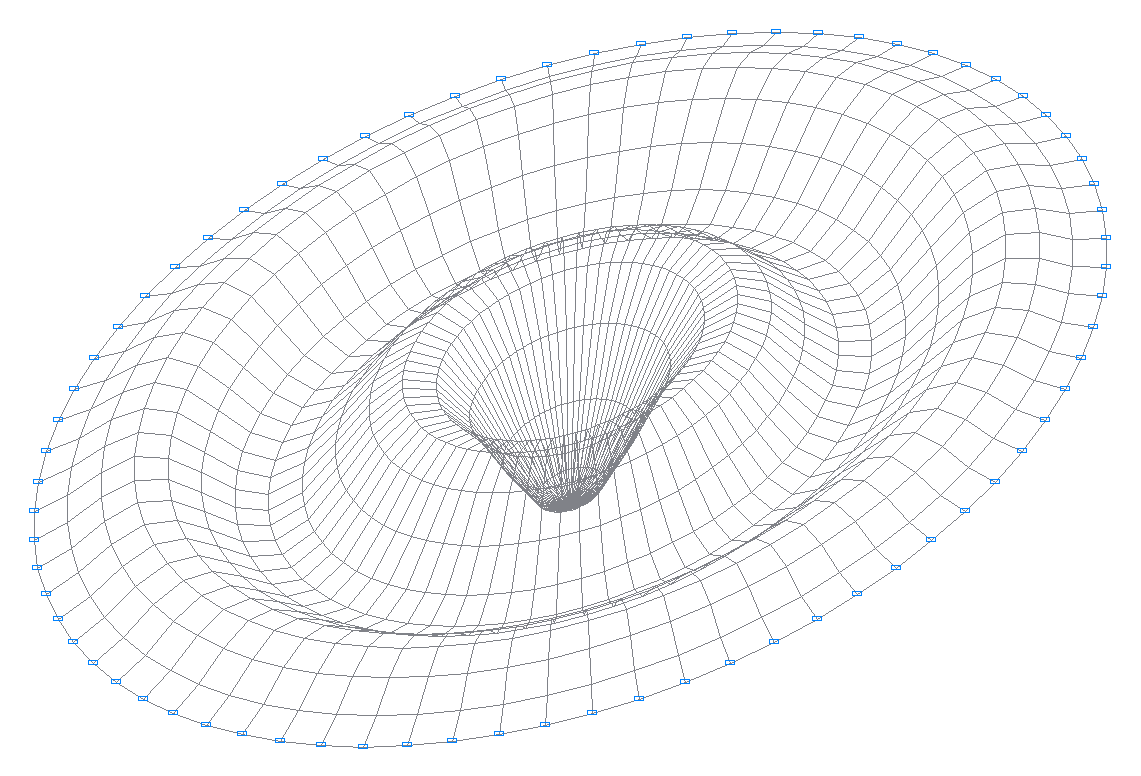
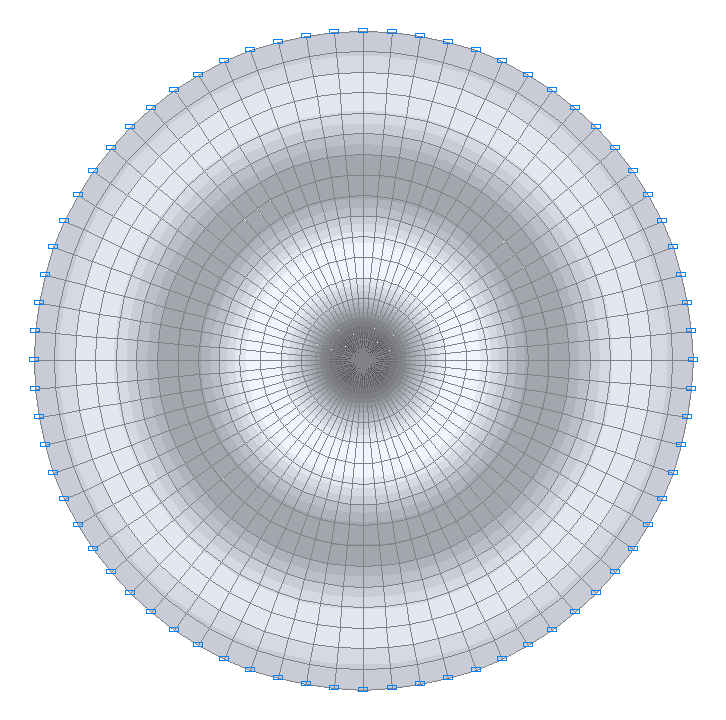

30-я собственная форма колебаний

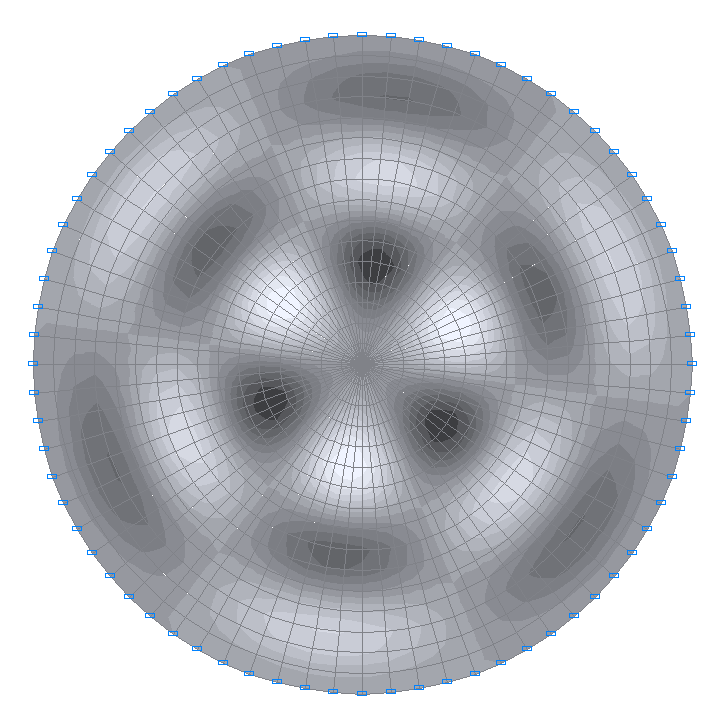

35-я собственная форма колебаний
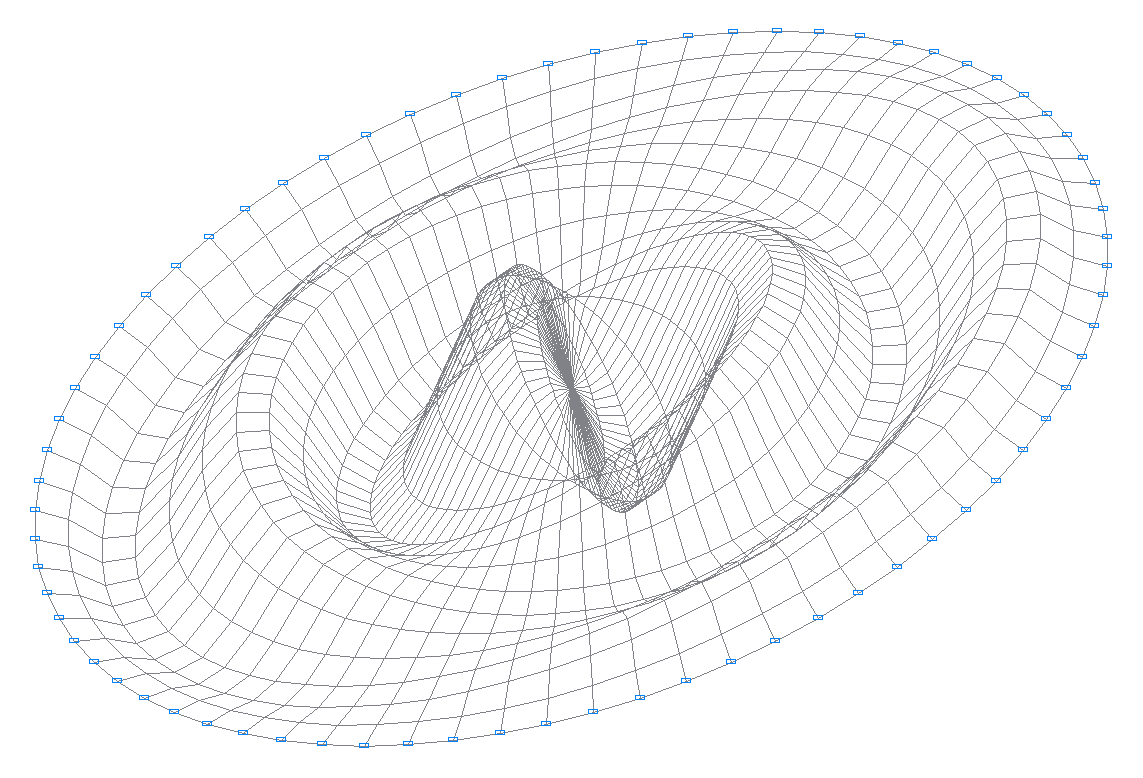


37-я собственная форма колебаний
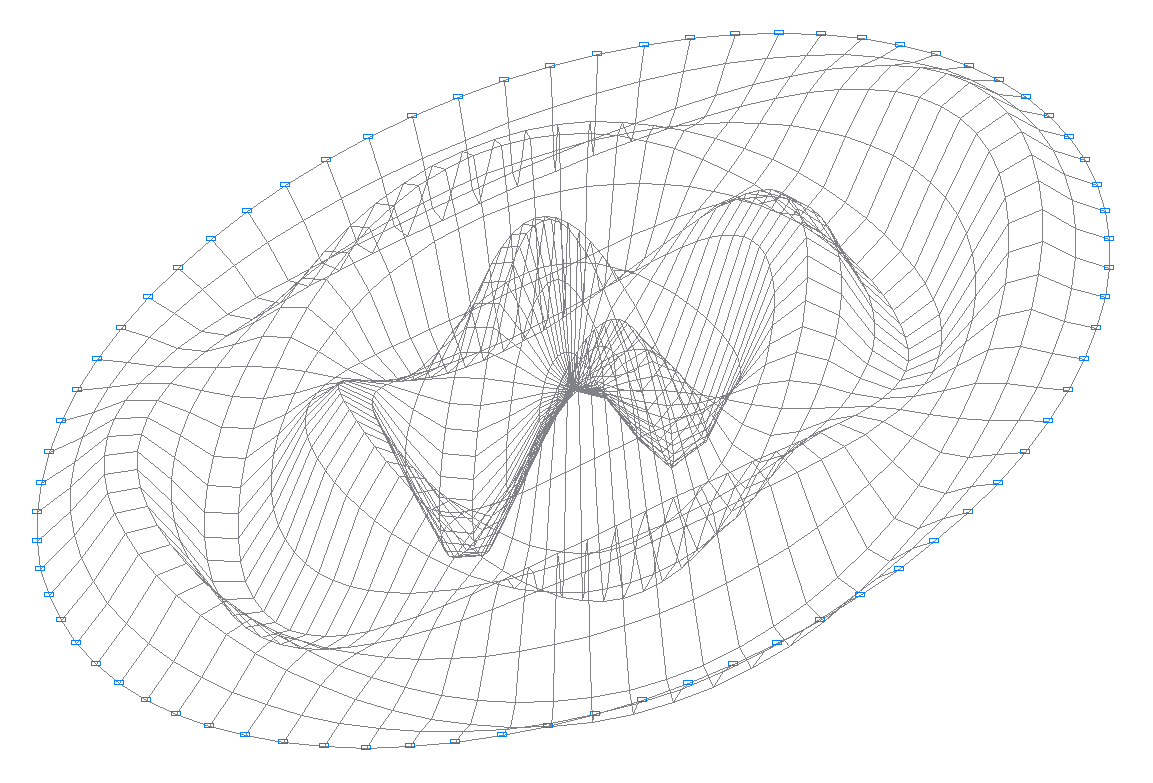


50-я (47-я теоретическая) собственная форма колебаний

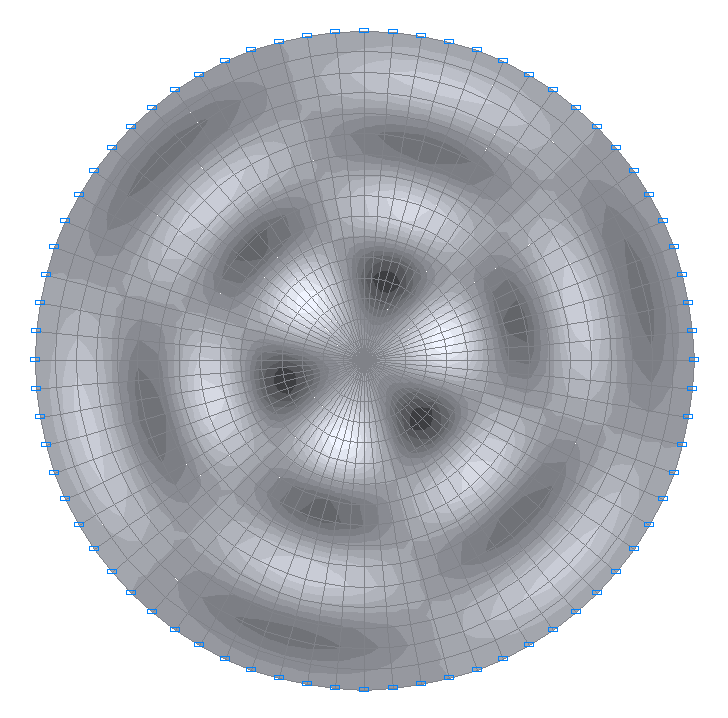

58-я собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, рад / с
|
Форма колебаний |
Число узловых окружностей m и диаметров n |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1 |
0, 0 |
633.5 |
633.8 |
0.05 |
|
2, 3 |
0, 1 |
1318.3 |
1321.7 |
0.26 |
|
4, 5 |
0, 2 |
2162.7 |
2170.6 |
0.37 |
|
6 |
1, 0 |
2466.1 |
2463.8 |
0.09 |
|
7, 8 |
0, 3 |
3164.3 |
3178.9 |
0.46 |
|
9, 10 |
1, 1 |
3771.9 |
3784.3 |
0.33 |
|
11, 12 |
0, 4 |
4319.8 |
4340.1 |
0.47 |
|
13, 14 |
1, 2 |
5244.8 |
5280.1 |
0.67 |
|
15 |
2, 0 |
5525.2 |
5511.5 |
0.25 |
|
16, 17 |
0, 5 |
5626.5 |
5655.5 |
0.52 |
|
18, 19 |
1, 3 |
6884.2 |
6931.9 |
0.69 |
|
20, 21 |
0, 6 |
7082.1 |
7123.6 |
0.59 |
|
22, 23 |
2, 1 |
7445.9 |
7477.9 |
0.43 |
|
24, 25 |
0, 7 |
8684.6 |
8742.7 |
0.67 |
|
26, 27 |
1, 4 |
8687.8 |
8748.6 |
0.70 |
|
28, 29 |
2, 2 |
9537.8 |
9652.0 |
1.20 |
|
30 |
3, 0 |
9808.7 |
9769.4 |
0.40 |
|
31, 32 |
0, 8 |
10432.5 |
10511.5 |
0.76 |
|
33, 34 |
1, 5 |
10653.2 |
10730.3 |
0.72 |
|
35, 36 |
2, 3 |
11800.3 |
11917.6 |
0.99 |
|
37, 38 |
0, 9 |
12324.5 |
12429.0 |
0.85 |
|
39, 40 |
3, 1 |
12342.9 |
12408.9 |
0.53 |
|
41, 42 |
1, 6 |
12778.0 |
12880.4 |
0.80 |
|
43, 44 |
2, 4 |
14232.0 |
14378.8 |
1.03 |
|
45, 46 |
0, 10 |
14359.4 |
14494.1 |
0.94 |
|
47, 48 |
3, 2 |
15050.6 |
15335.5 |
1.89 |
|
49, 50 |
1, 7 |
15060.4 |
15196.7 |
0.91 |
|
51 |
4, 0 |
15316.4 |
15229.9 |
0.56 |
|
52, 53 |
0, 11 |
16536.2 |
16705.2 |
1.02 |
|
54, 55 |
2, 5 |
16830.7 |
17001.7 |
1.02 |
|
56, 57 |
1, 8 |
17498.5 |
17677.4 |
1.02 |
|
58, 59 |
3, 3 |
17931.5 |
18171.2 |
1.34 |
|
60, 61 |
4, 1 |
18463.5 |
18580.3 |
0.63 |
Замечания: При аналитическом решении собственные частоты колебаний ω круговой жестко защемленной по контуру пластины с плотностью материала ρ могут быть определены из следующего уравнения, полученного на основе метода факторизации:
\[ \frac{J_{n+1} \left( {\beta \cdot R} \right)}{J_{n} \left( {\beta \cdot R} \right)}+\frac{I_{n+1} \left( {\beta \cdot R} \right)}{I_{n} \left( {\beta \cdot R} \right)}=0,\quad где: \] \[ \beta =\left( {\frac{\rho \cdot h\cdot \omega^{2}}{D}} \right)^{\frac{1}{4}}, \quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad n=0,1,2,3, ... \quad -\quad число \quad узловых \quad диаметров, \] \[ J_{n} \left( {\beta \cdot R} \right), \quad J_{n+1} \left( {\beta \cdot R} \right)\quad -\quad значения \quad функции \quad Бесселя \quad первого \quad рода \quad n-го \quad порядка, \] \[ I_{n} \left( {\beta \cdot R} \right), \quad I_{n+1} \left( {\beta \cdot R} \right)\quad -\quad значения \quad модифицированной \quad функции \quad Бесселя \quad первого \quad рода \quad n-го \quad порядка. \]
