Свободные колебания прямоугольной шарнирно опертой по периметру пластины
Цель: Модальный анализ прямоугольной шарнирно опертой по периметру пластины.
Формулировка задачи: Определить собственные формы и частоты колебаний ω прямоугольной шарнирно опертой по периметру пластины с плотностью материала ρ.
Ссылки: И. А. Биргер, Я. Г. Пановко, Прочность, устойчивость, колебания, Справочник в трех томах, Том 3, Москва, Машиностроение, 1968, стр. 375.
Исходные данные:
| E = 2.06·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 7.85 т/м3 | - плотность материала; |
| h = 0.01 м | - толщина пластины; |
| a1 = 1.5 м | - размер длинной стороны пластины (вдоль оси X общей системы координат); |
| a2 = 1.0 м | - размер короткой стороны пластины (вдоль оси Y общей системы координат). |
Файл с исходными данными: 5.3.spr
Конечноэлементная модель: Расчетная схема – балочный ростверк / плита, 600 элементов плиты типа 20. Сетка конечных элементов разбита по длинам сторон пластины (вдоль осей X, Y общей системы координат) с шагом 0.05 м. Обеспечение граничных условий достигается за счет наложения связей по направлению степени свободы Z для кромок, расположенных вдоль осей X и Y общей системы координат. Распределенная масса задается преобразованием статической нагрузки от собственного веса пластины ow = γ•h, где γ = ρ•g = 77.01 кН/м3. Количество узлов в расчетной схеме – 651. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD
Расчетная схема
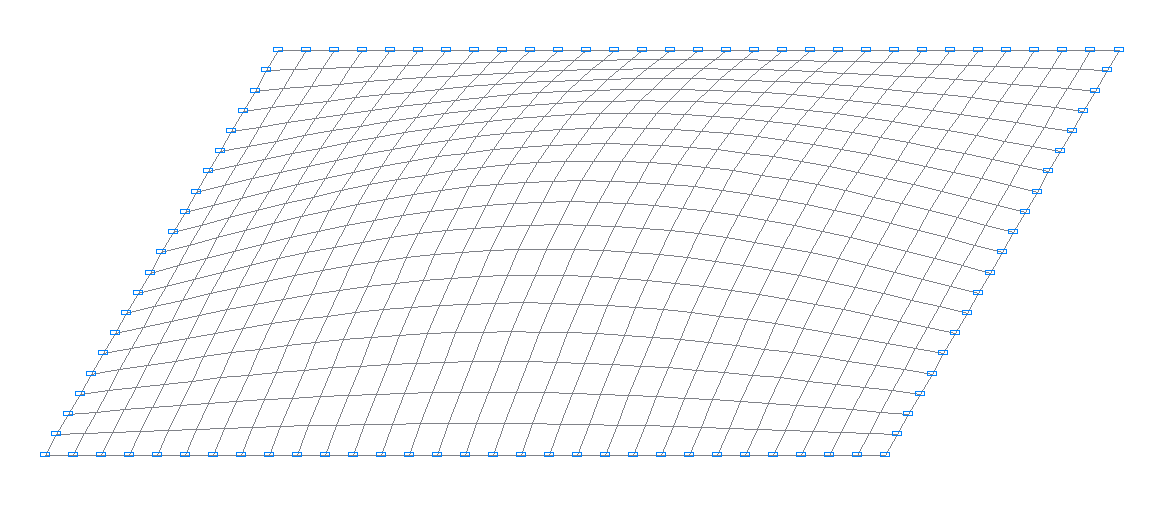


1-я собственная форма колебаний
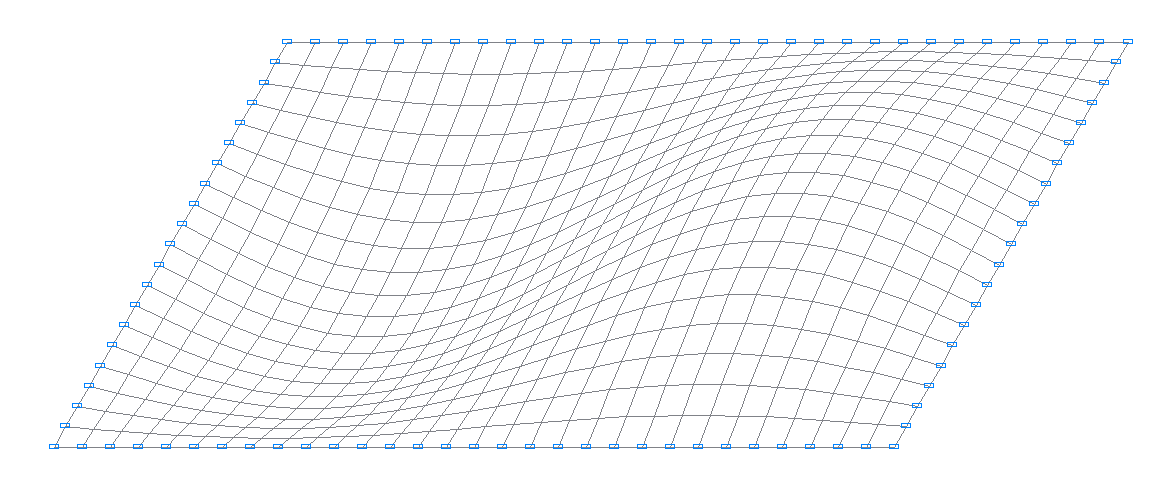


2-я собственная форма колебаний
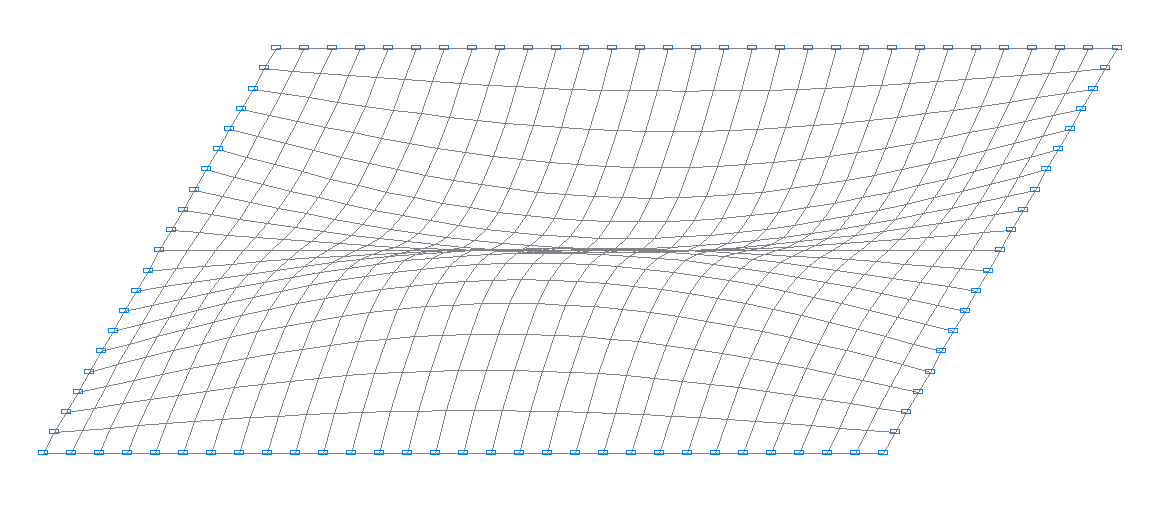
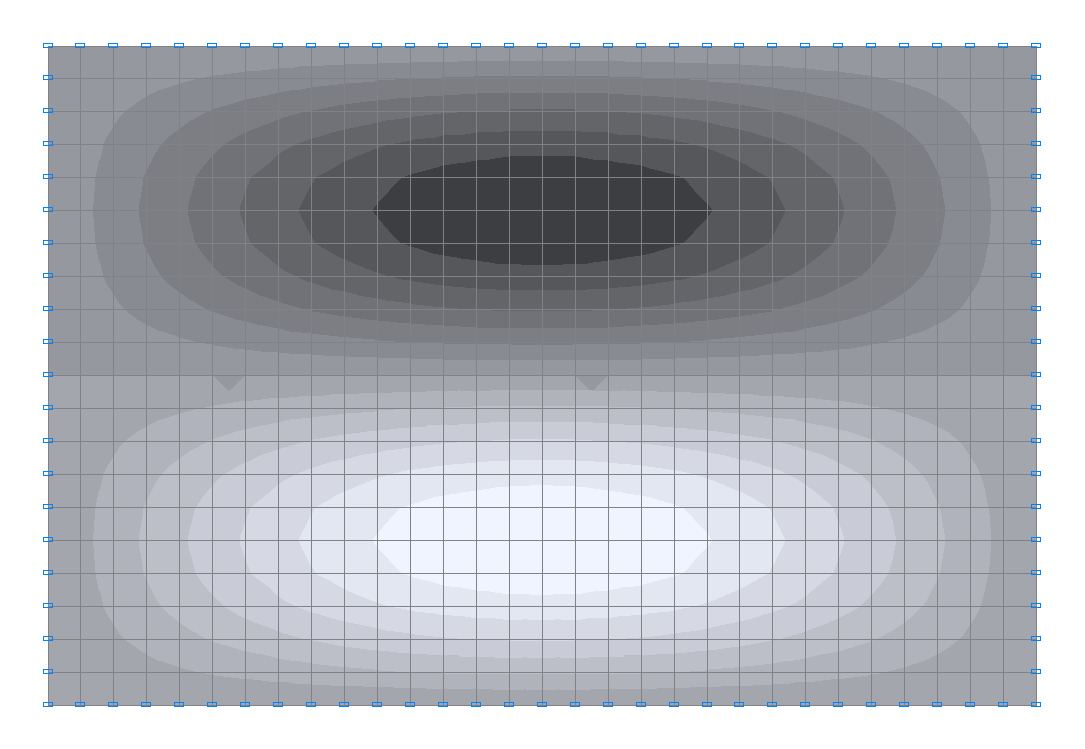
3-я собственная форма колебаний
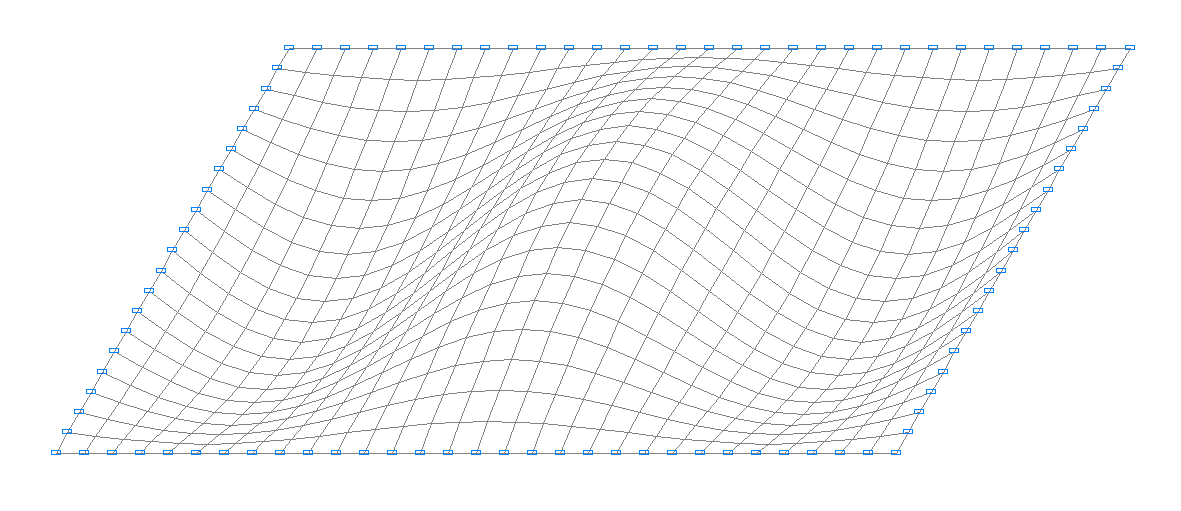
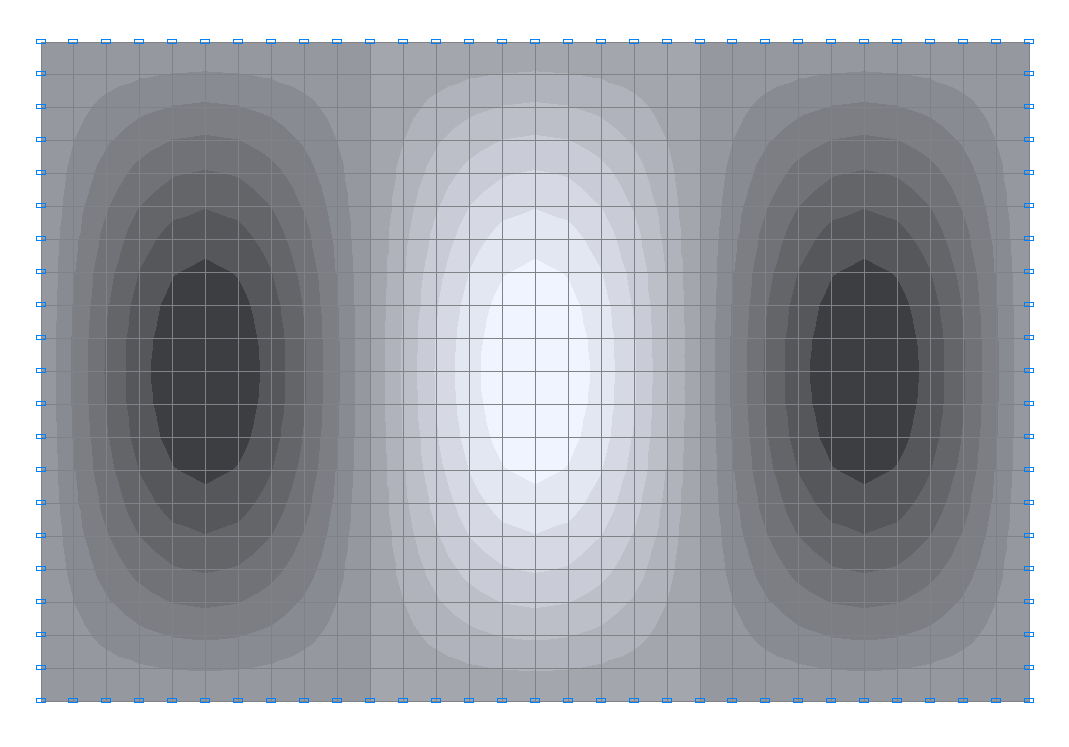

4-я собственная форма колебаний
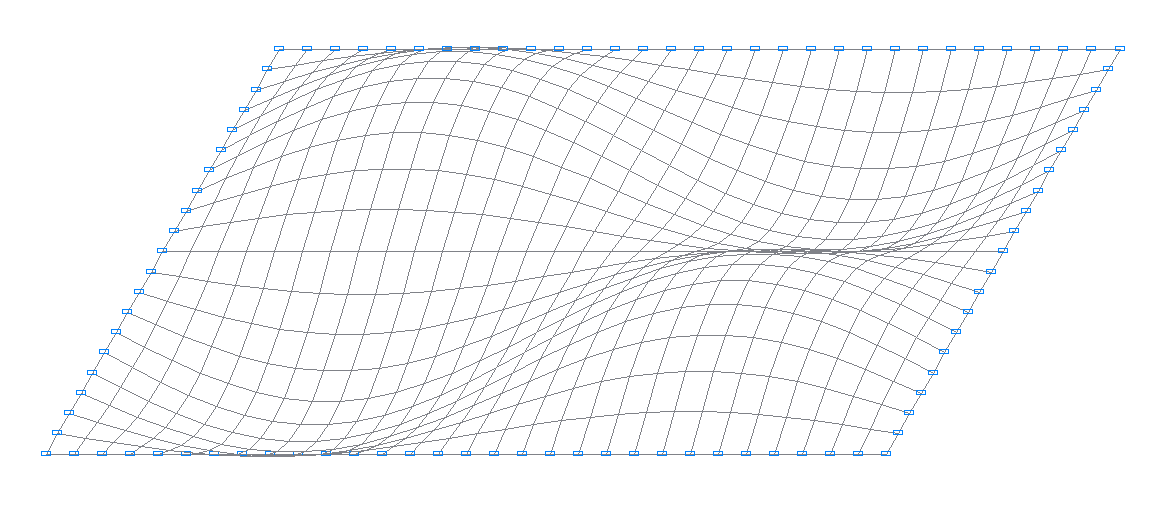
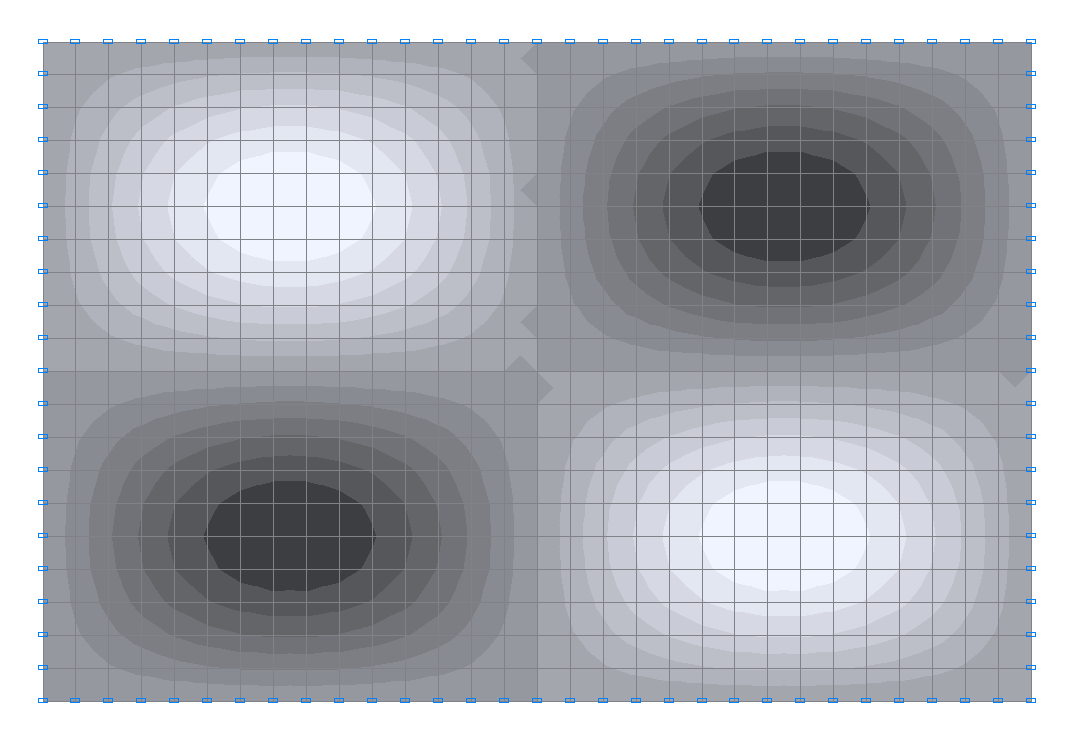

5-я собственная форма колебаний
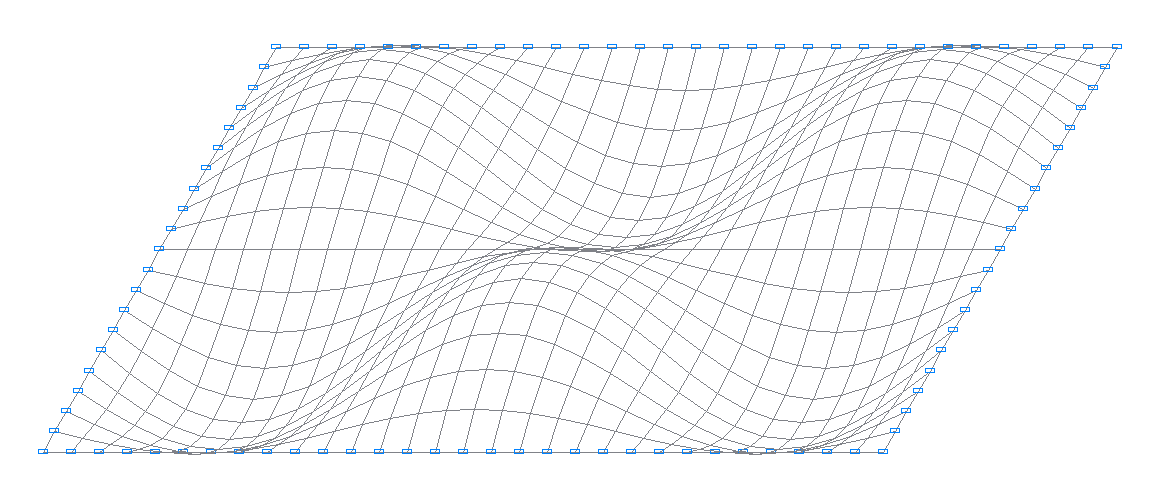


6-я собственная форма колебаний
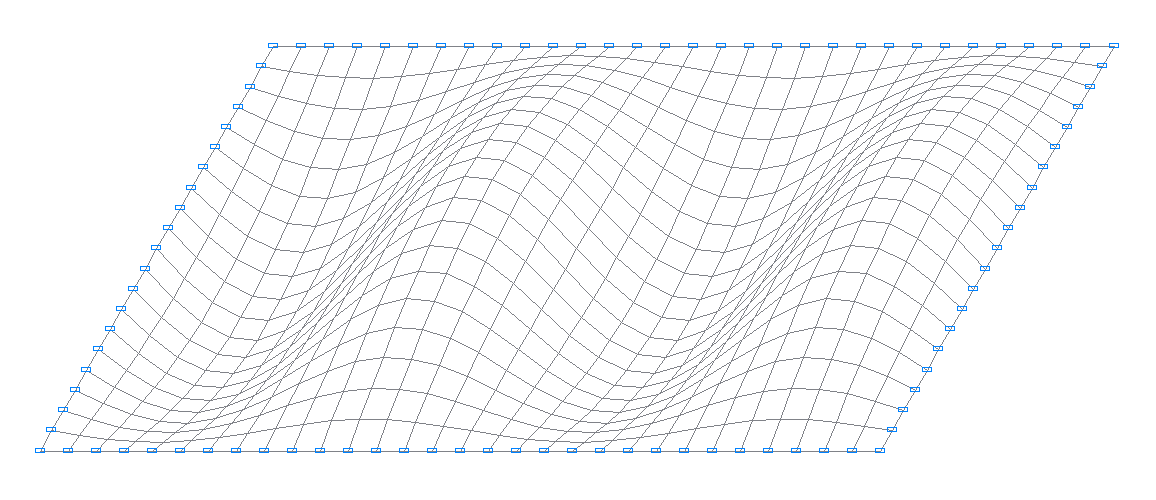
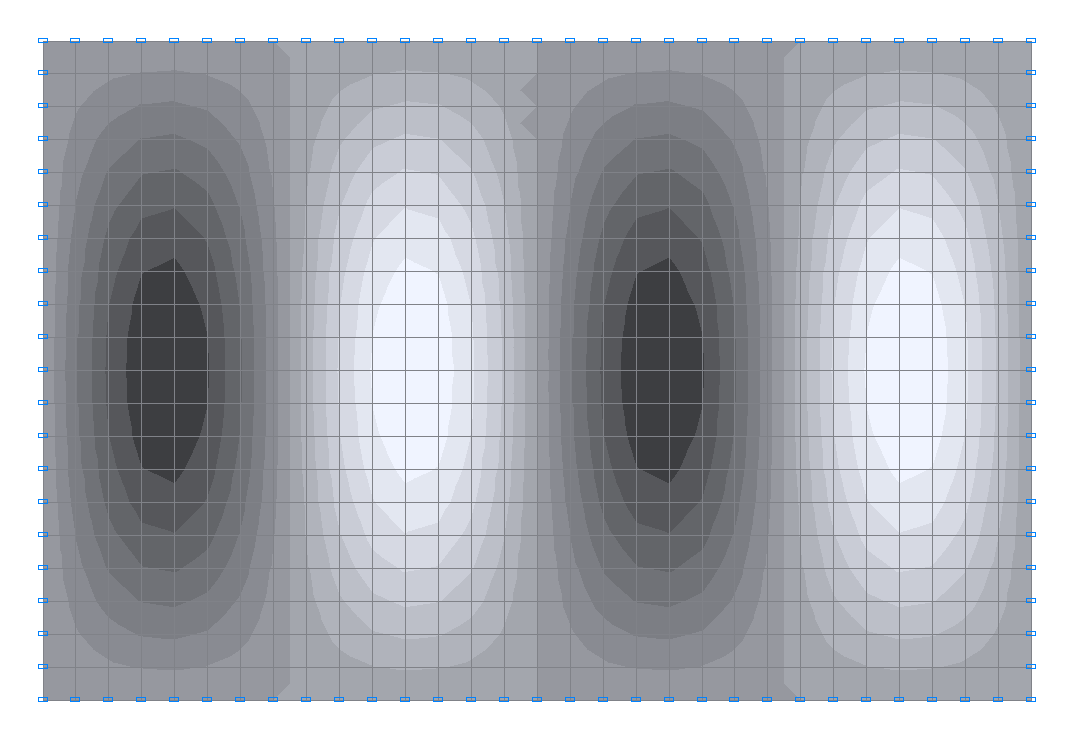

7-я собственная форма колебаний
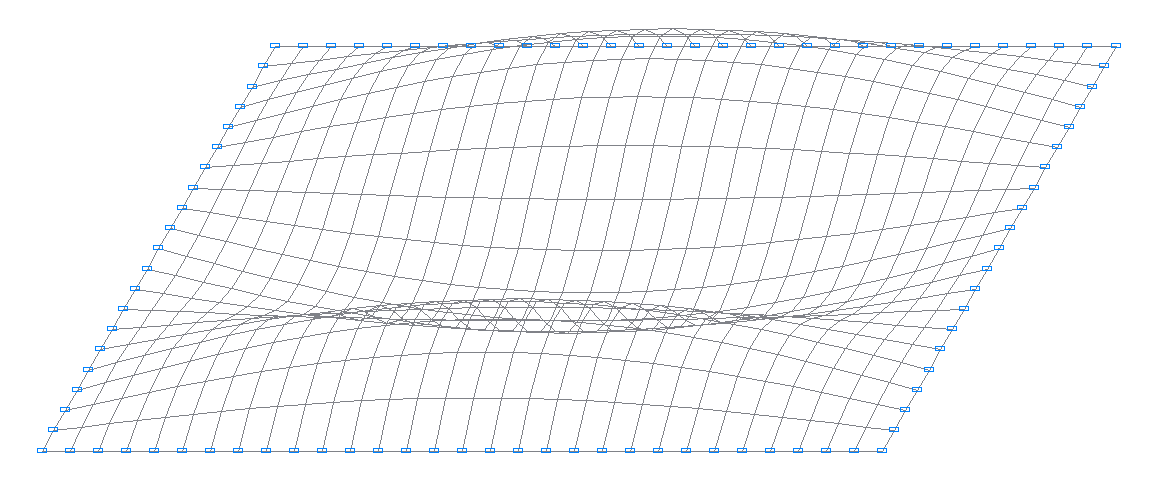
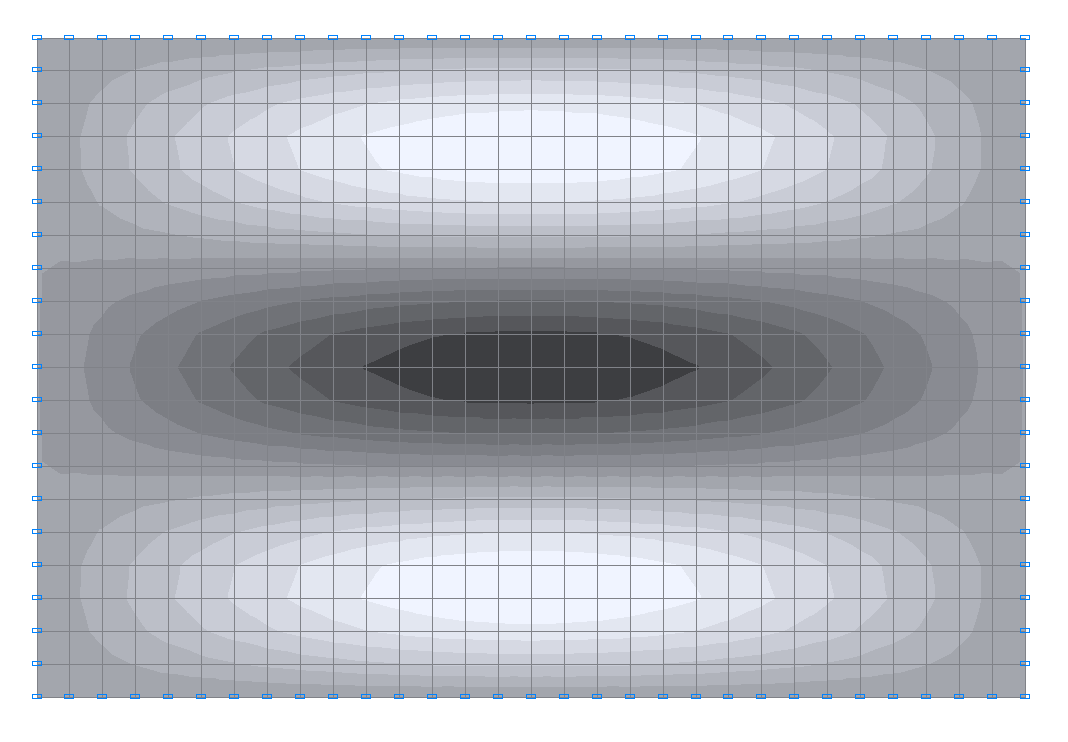

8-я собственная форма колебаний
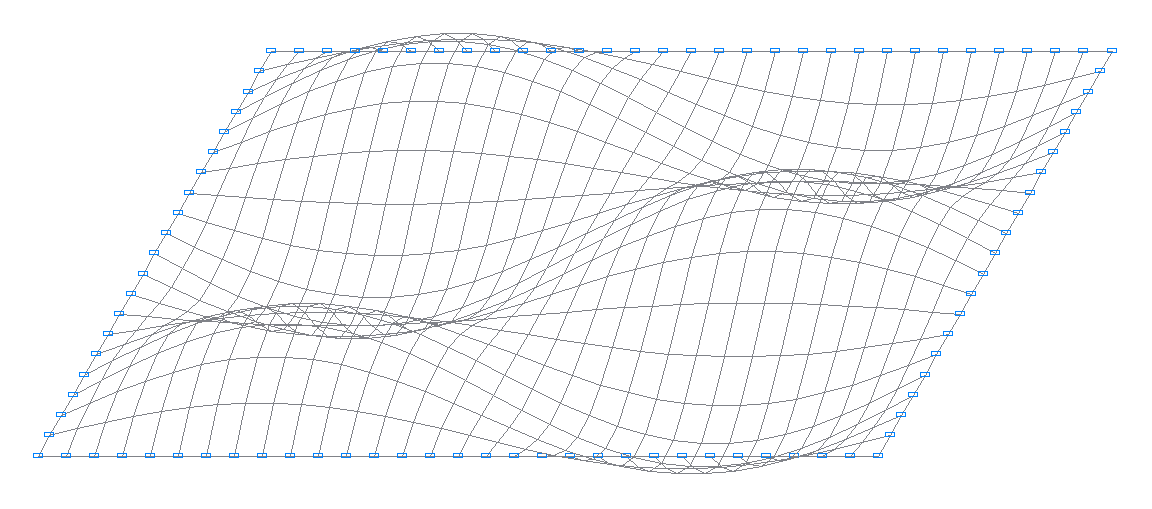


9-я собственная форма колебаний
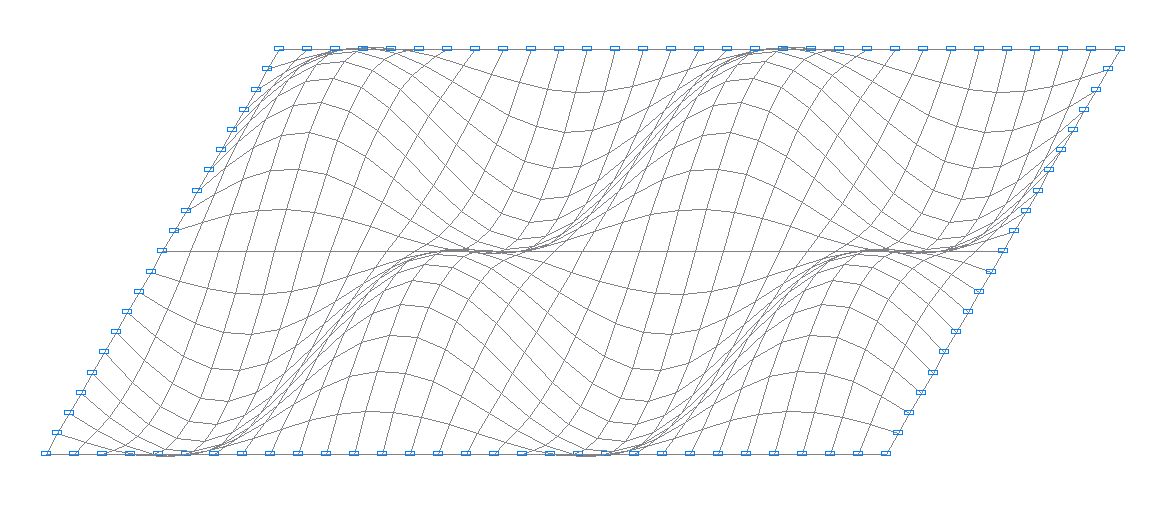


10-я собственная форма колебаний
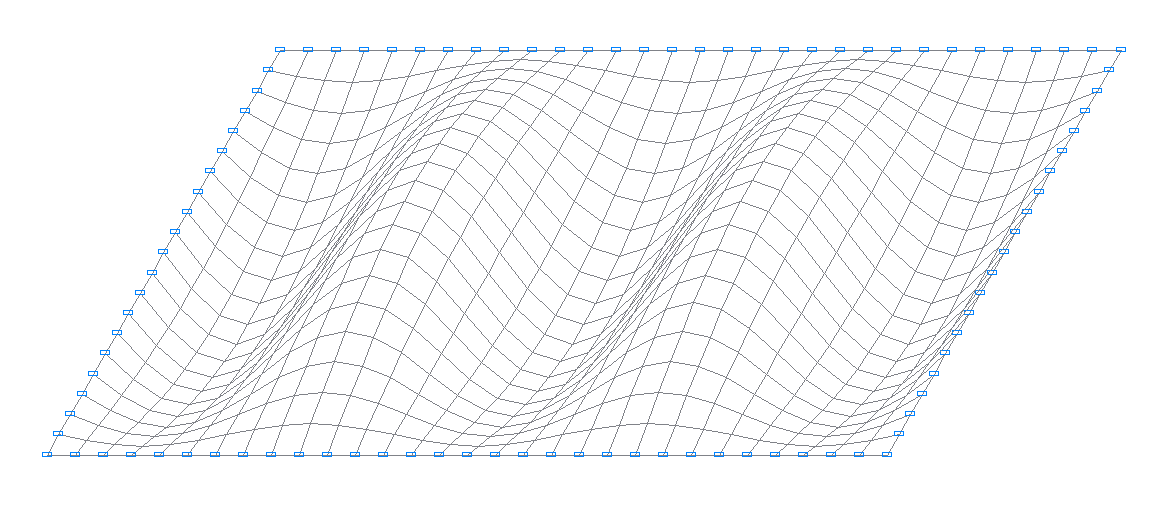
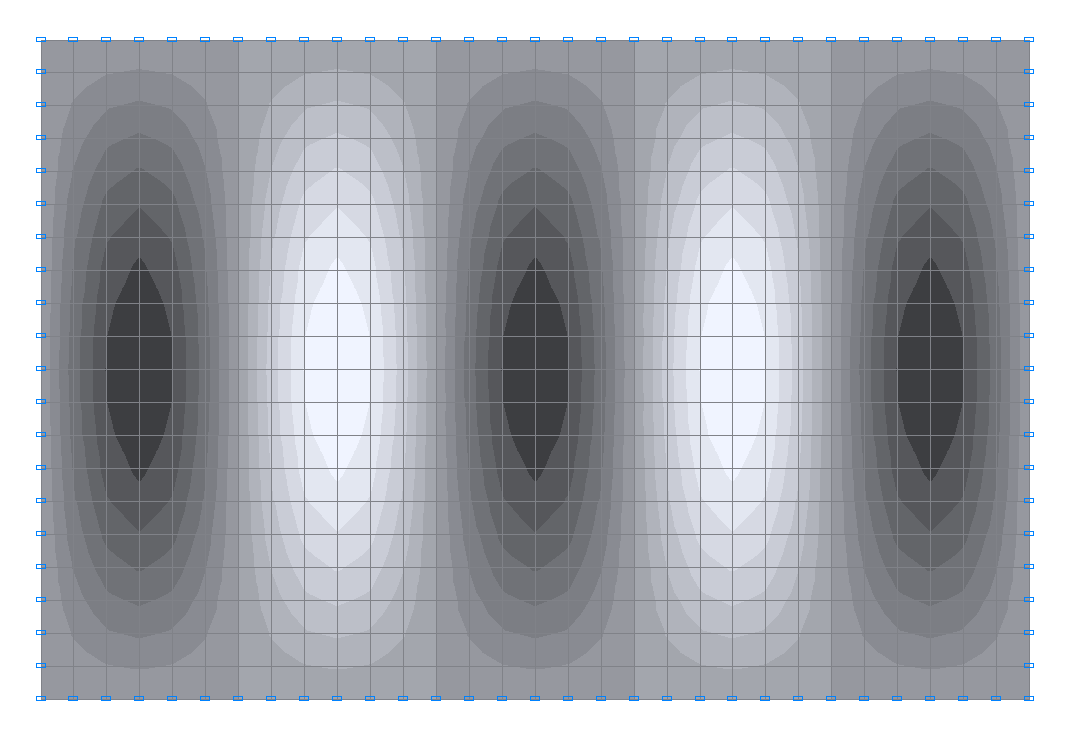

11-я собственная форма колебаний
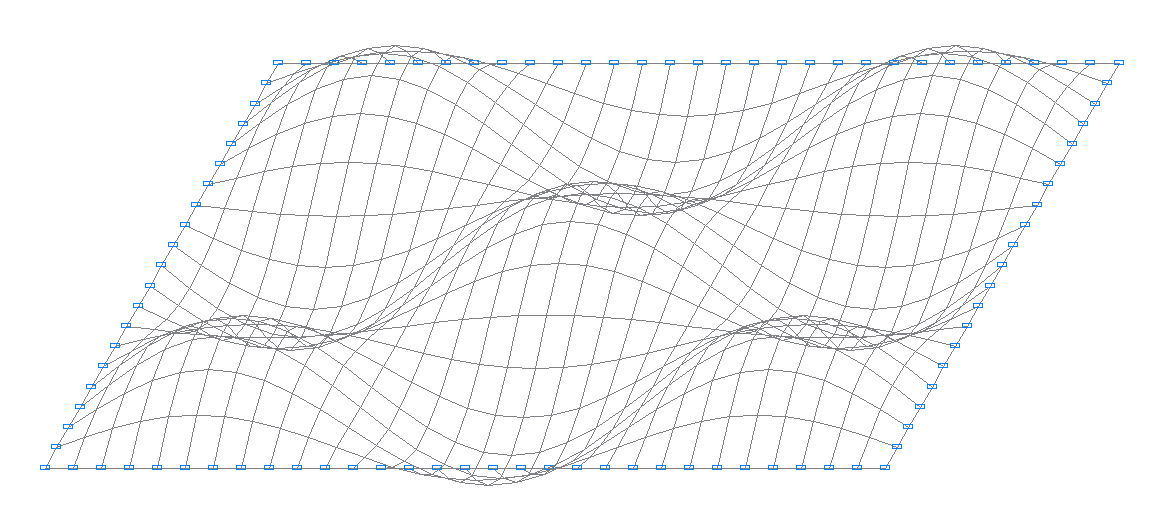


12-я собственная форма колебаний
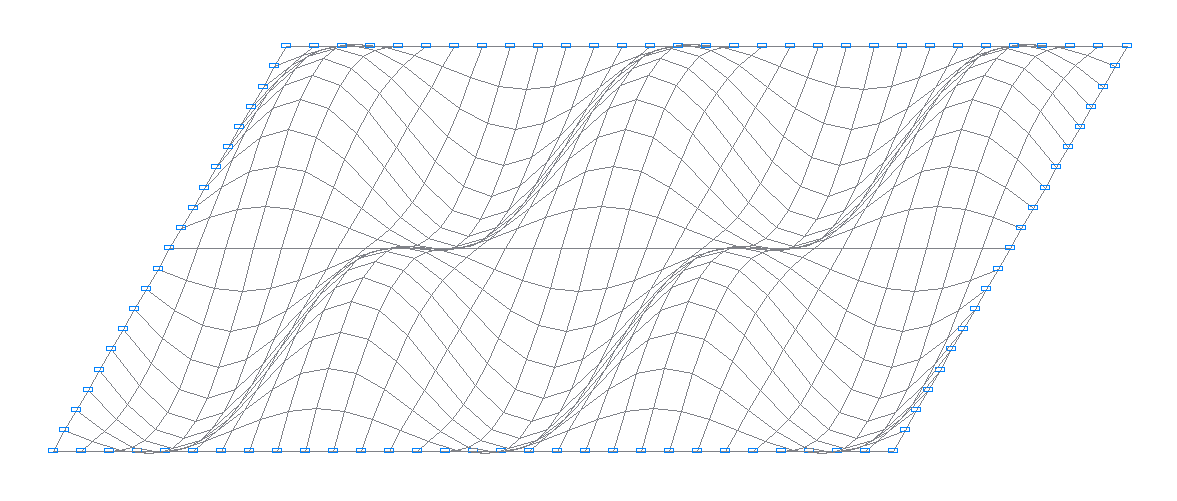


13-я собственная форма колебаний
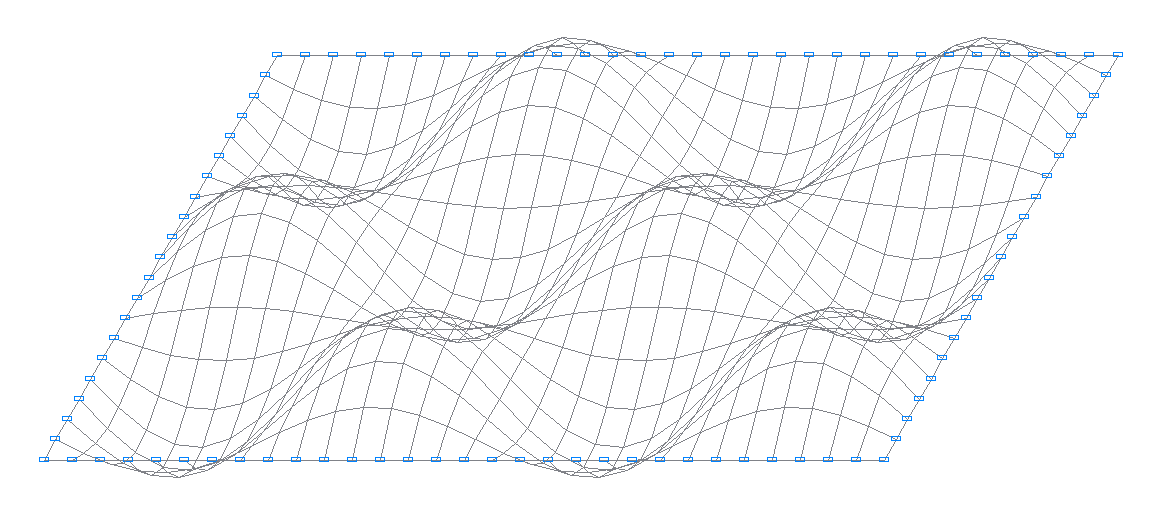


14-я собственная форма колебаний

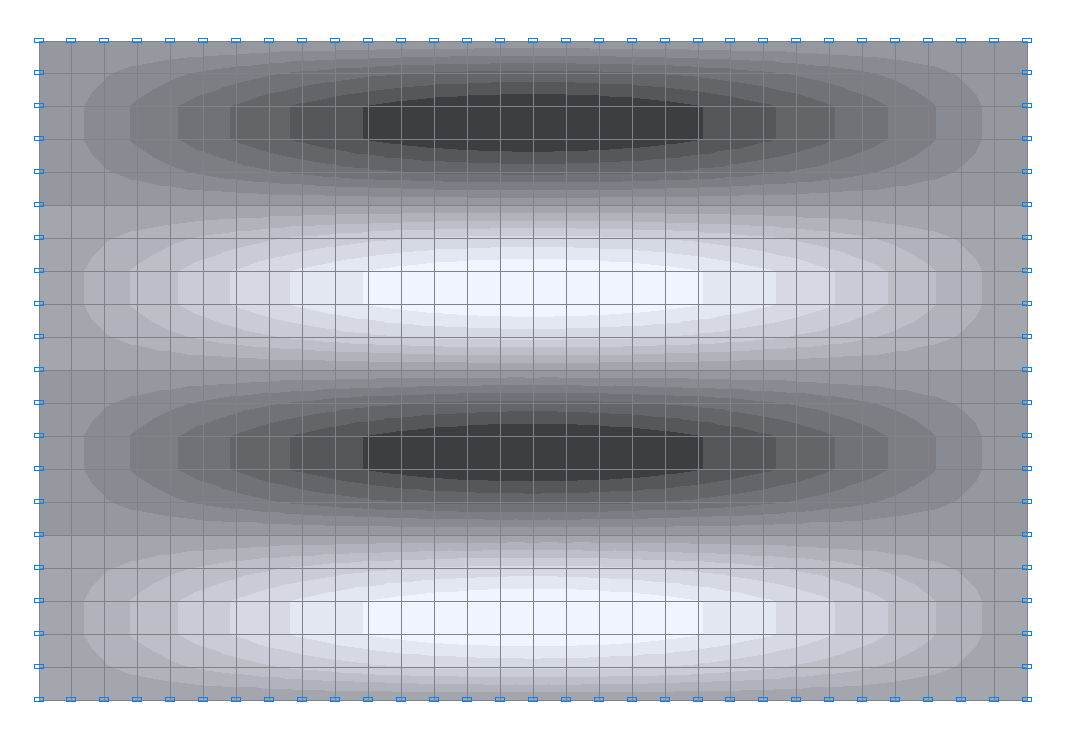

15-я собственная форма колебаний
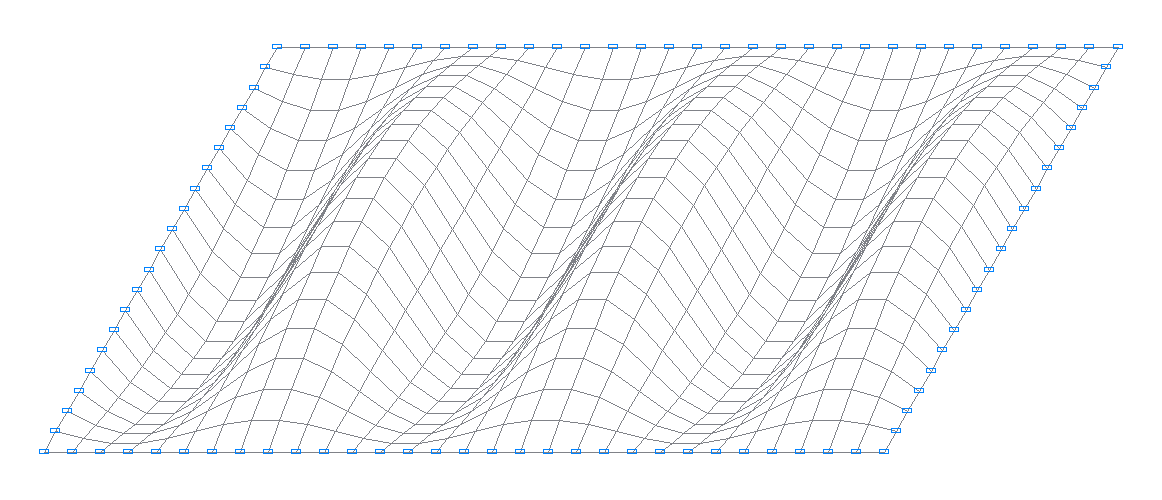
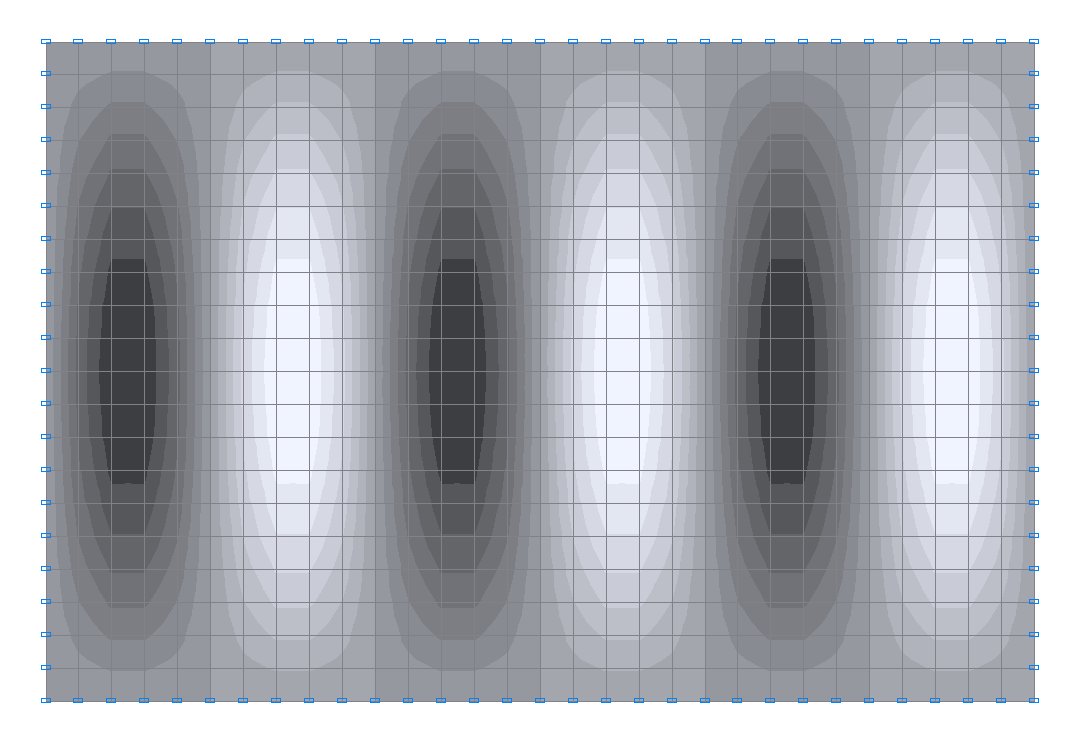

16-я собственная форма колебаний
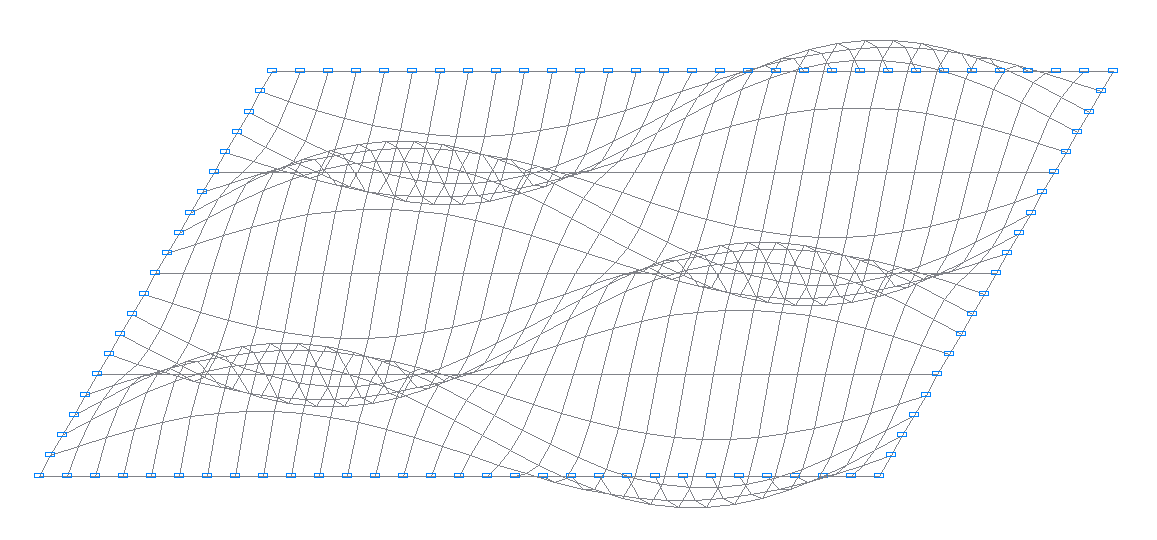
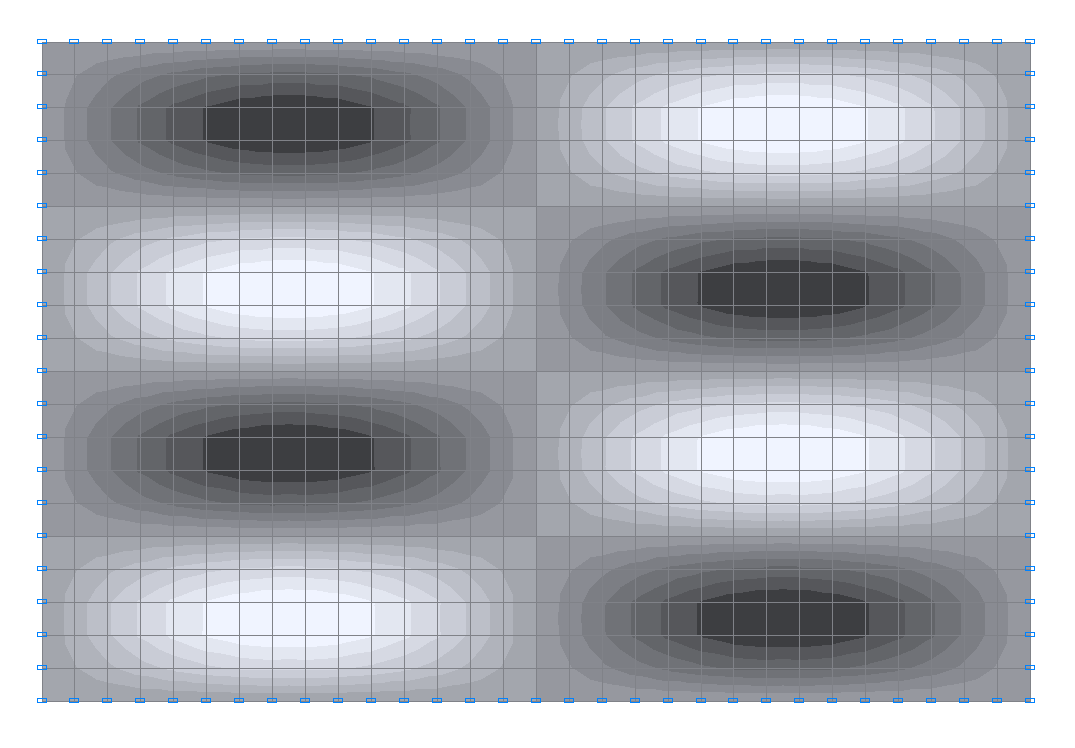

17-я собственная форма колебаний
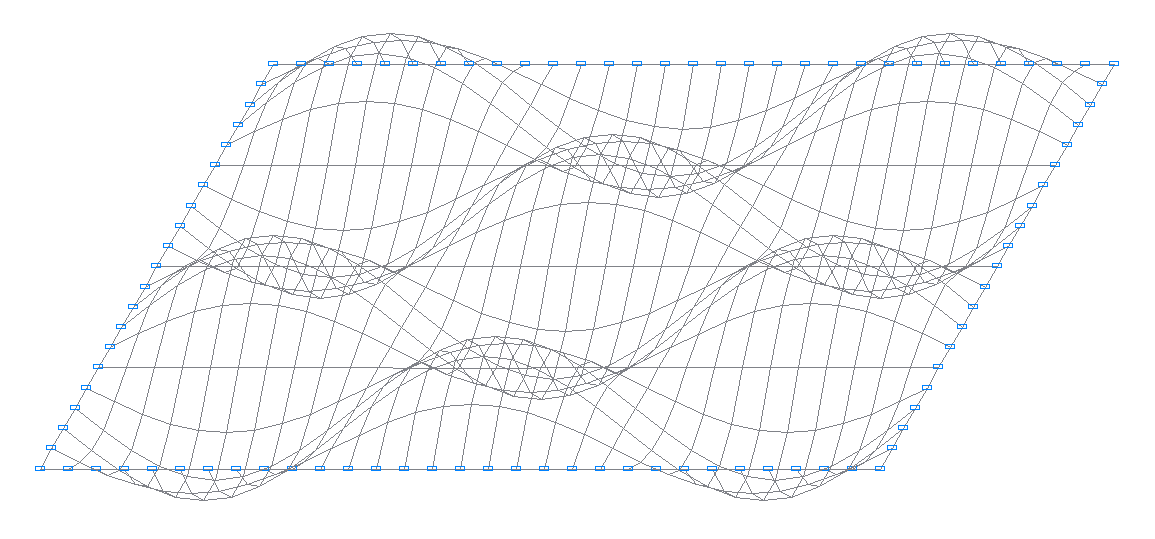

18-я собственная форма колебаний
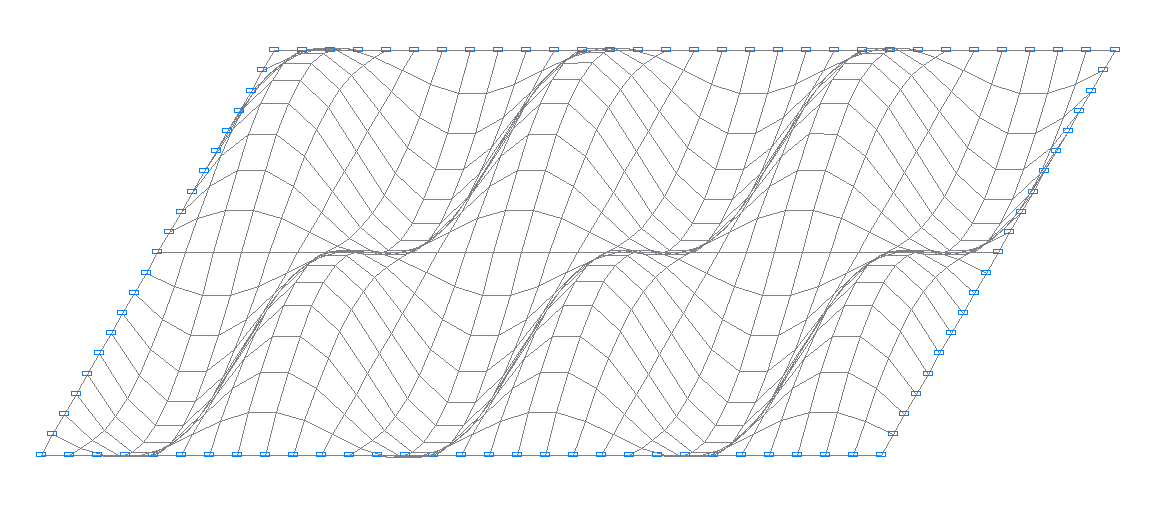


19-я собственная форма колебаний
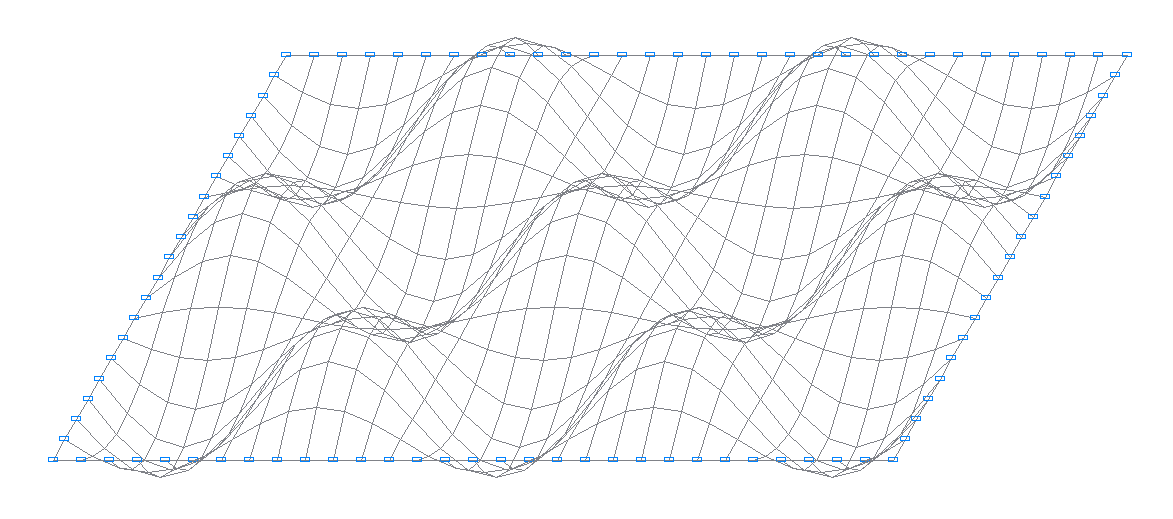


20-я собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, рад / с
|
Форма колебаний |
Число полуволн m1, m2 |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1 |
1, 1 |
221.0 |
221.1 |
0.05 |
|
2 |
2, 1 |
425.0 |
425.3 |
0.07 |
|
3 |
1, 2 |
678.0 |
680.3 |
0.34 |
|
4 |
3, 1 |
765.0 |
765.6 |
0.08 |
|
5 |
2, 2 |
884.0 |
885.1 |
0.12 |
|
6 |
3, 2 |
1224.0 |
1226.4 |
0.20 |
|
7 |
4, 1 |
1241.0 |
1242.0 |
0.08 |
|
8 |
1, 3 |
1445.0 |
1445.5 |
0.03 |
|
9 |
2, 3 |
1649.0 |
1651.4 |
0.15 |
|
10 |
4, 2 |
1700.0 |
1704.3 |
0.25 |
|
11 |
5, 1 |
1853.0 |
1854.6 |
0.09 |
|
12 |
3, 3 |
1989.0 |
1994.5 |
0.28 |
|
13 |
5, 2 |
2312.0 |
2318.8 |
0.29 |
|
14 |
4, 3 |
2465.0 |
2474.9 |
0.40 |
|
15 |
1, 4 |
2516.0 |
2516.8 |
0.03 |
|
16 |
6, 1 |
2601.0 |
2603.1 |
0.08 |
|
17 |
2, 4 |
2720.0 |
2724.1 |
0.15 |
|
18 |
3, 4 |
3060.0 |
3069.7 |
0.32 |
|
19 |
6, 2 |
3060.0 |
3069.7 |
0.32 |
|
20 |
5, 3 |
3077.0 |
3092.5 |
0.50 |
Замечания: При аналитическом решении собственные частоты ω колебаний прямоугольной шарнирно опертой по периметру пластины с плотностью материала ρ могут быть вычислены по следующей формуле:
\[ \omega =\pi^{2}\cdot \left( {\frac{m_{1}^{2}}{a_{2}^{2}}+\frac{m_{2} ^{2}}{a_{2}^{2}}} \right)\cdot \left( {\frac{D}{\rho \cdot h}} \right)^{\frac{1}{2}},\quad где: \quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu ^{2}} \right)}, \quad m_{1} ,m_{2} =1,2,3, ... \]
