Свободные колебания квадратной жестко защемленной по периметру пластины
Цель: Модальный анализ квадратной защемленной по периметру пластины.
Файл с исходными данными: 5.4.spr
Формулировка задачи: Определить собственные формы и частоты колебаний ω квадратной защемленной по периметру пластины с плотностью материала ρ.
Ссылки: И. А. Биргер, Я. Г. Пановко, Прочность, устойчивость, колебания, Справочник в трех томах, Том 3, Москва, Машиностроение, 1968, стр. 377.
Исходные данные:
| E = 2.06·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 7.85 т/м3 | - плотность материала; |
| h = 0.01 м | - толщина пластины; |
| a1 = 1.0 м | - размер длинной стороны пластины (вдоль оси X общей системы координат); |
| a2 = 1.0 м | - размер короткой стороны пластины (вдоль оси Y общей системы координат). |
Конечноэлементная модель: Расчетная схема – балочный ростверк / плита, 400 элементов плиты типа 20. Сетка конечных элементов разбита по длинам сторон пластины (вдоль осей X, Y общей системы координат) с шагом 0.05 м. Обеспечение граничных условий достигается за счет наложения связей по направлению степеней свободы Z, UX, UY для кромок, расположенных вдоль осей X и Y общей системы координат. Распределенная масса задается преобразованием статической нагрузки от собственного веса пластины ow = γ∙h, где γ = ρ∙g = 77.01 кН/м3. Количество узлов в расчетной схеме – 441. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD
Расчетная схема
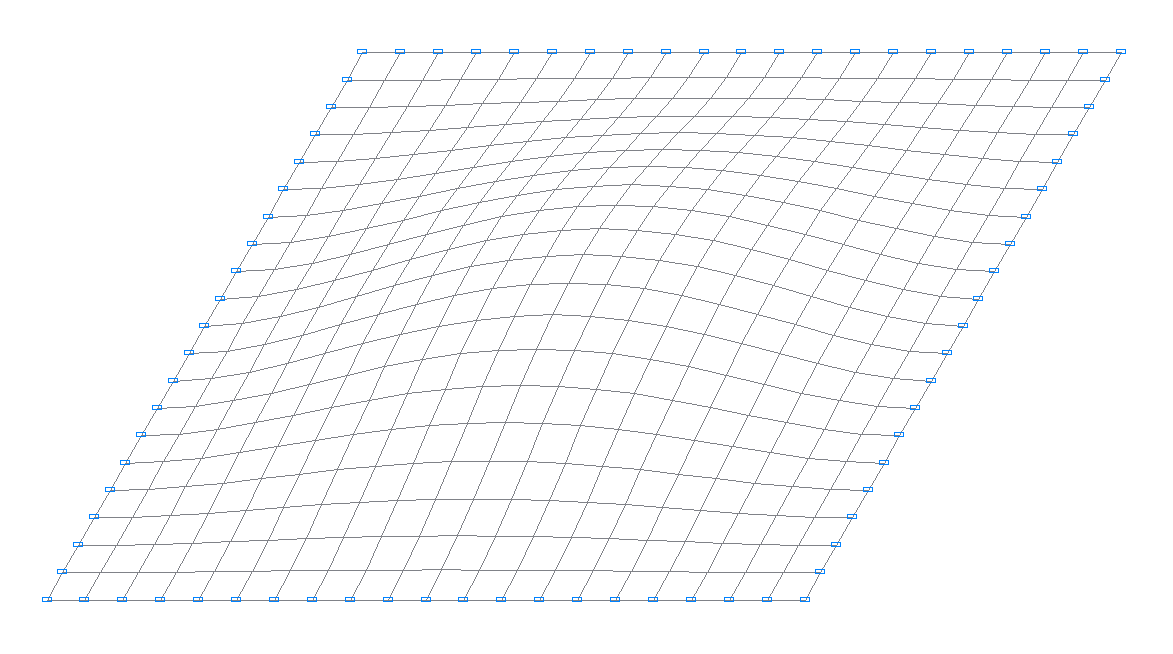
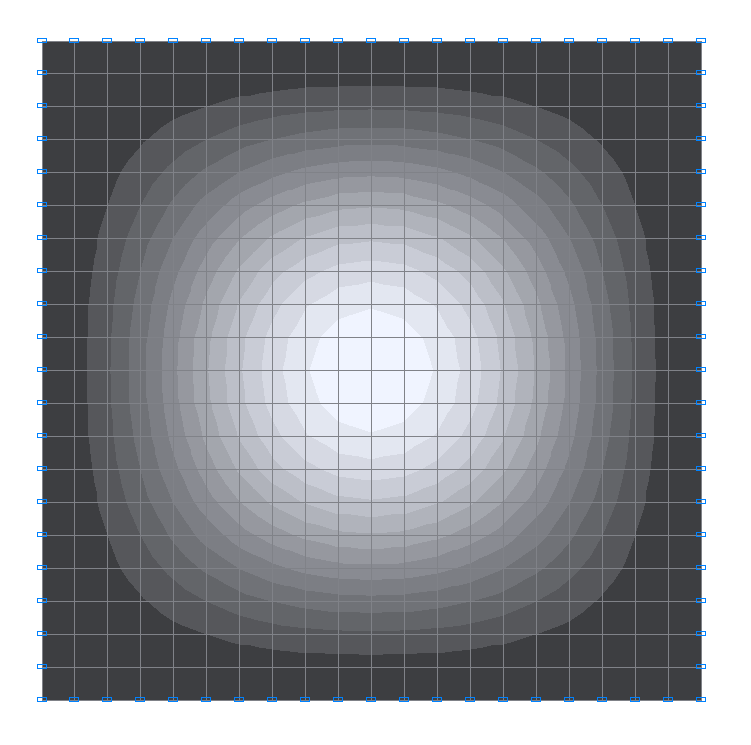
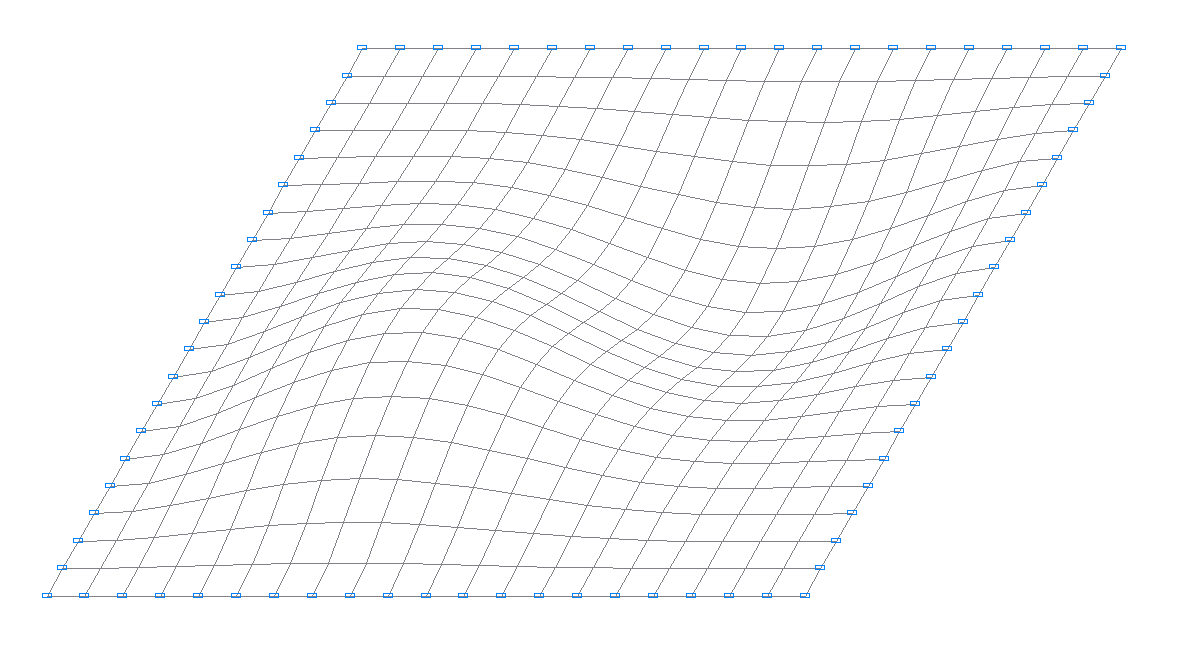
1-я собственная форма колебаний
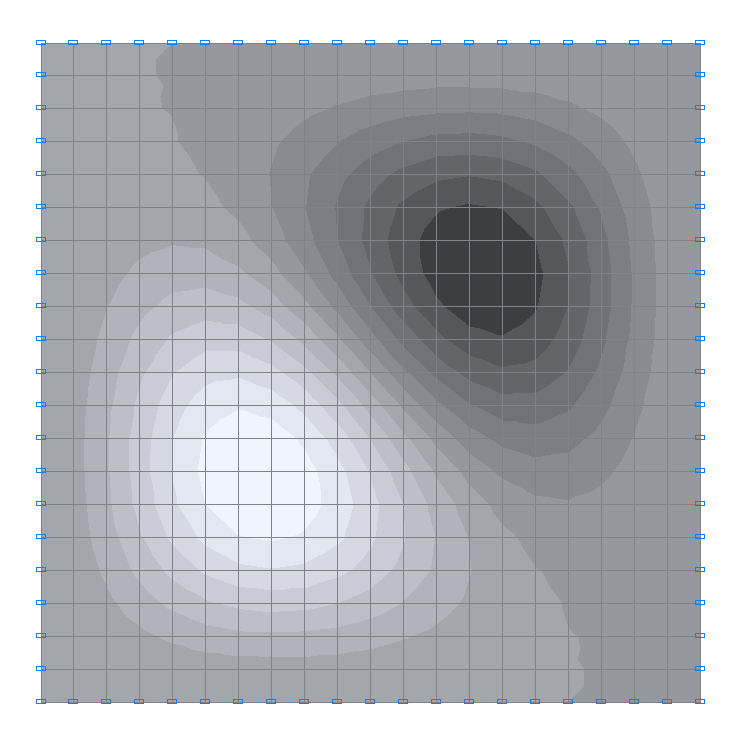

2-я собственная форма колебаний
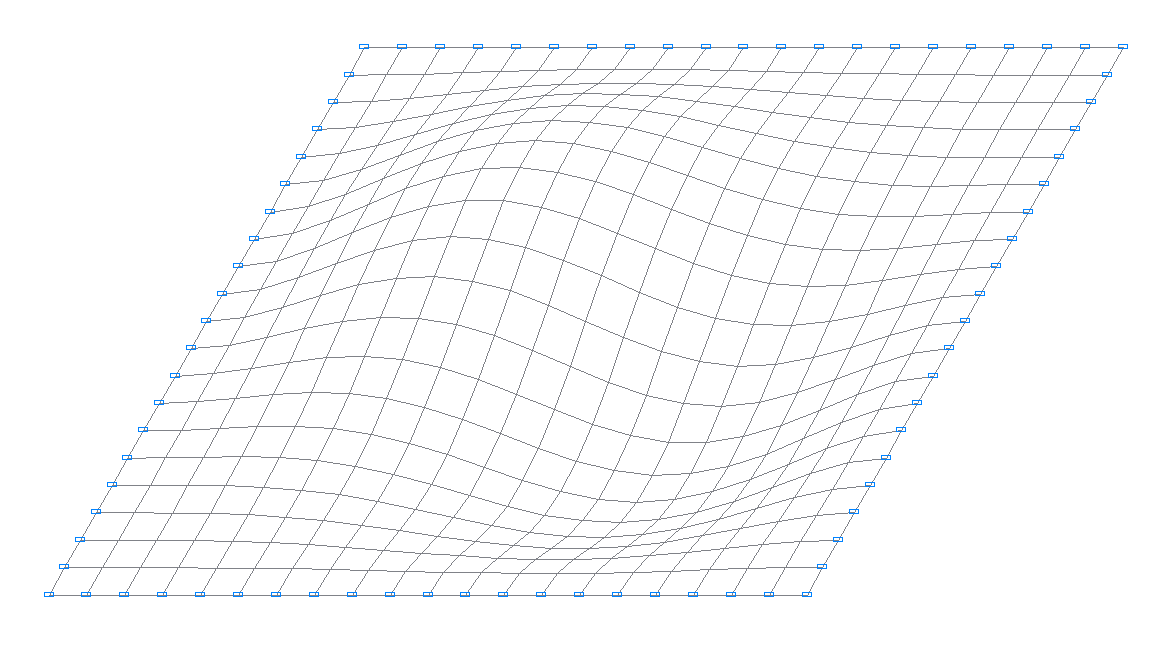
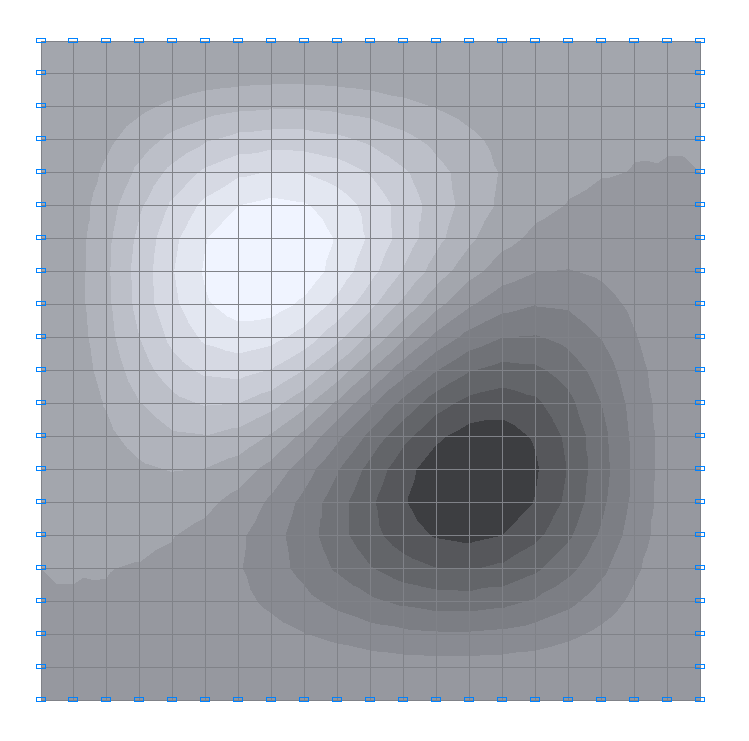

3-я собственная форма колебаний
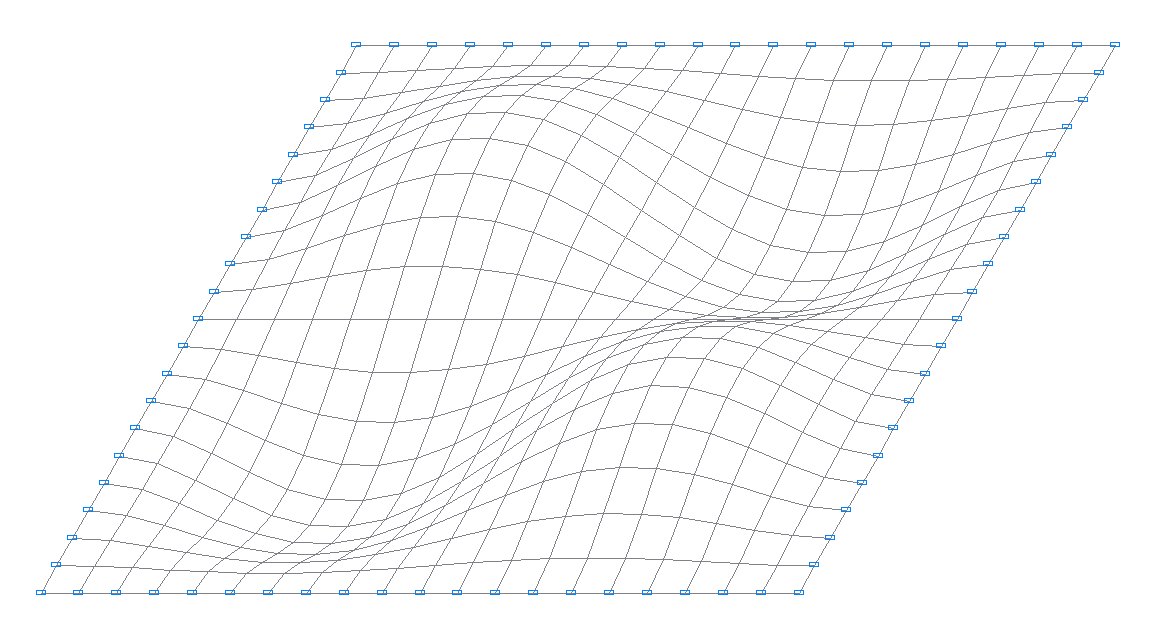


4-я собственная форма колебаний
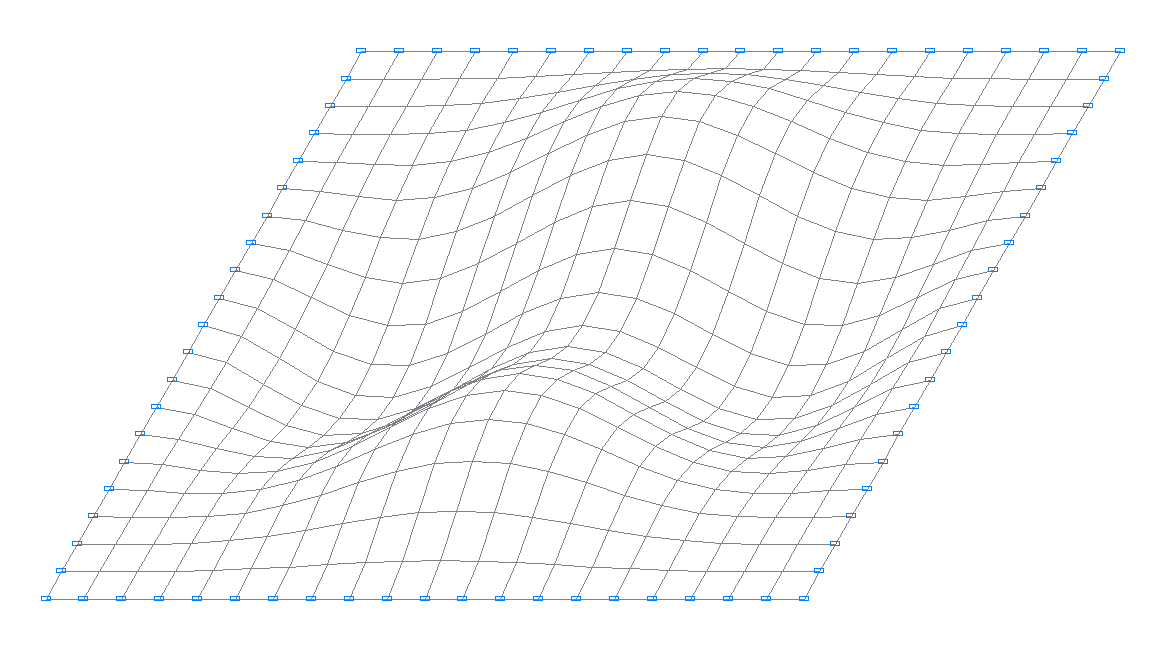
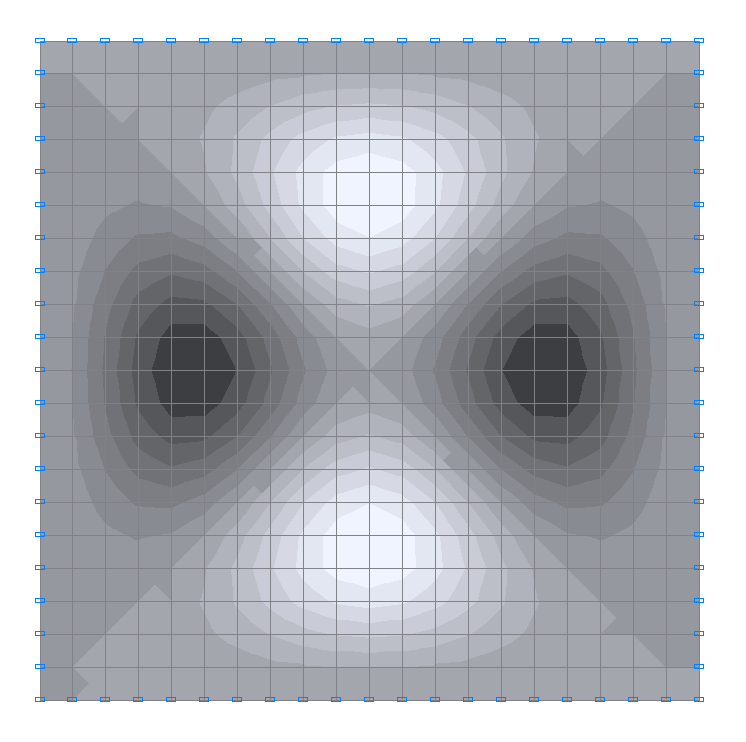

5-я собственная форма колебаний
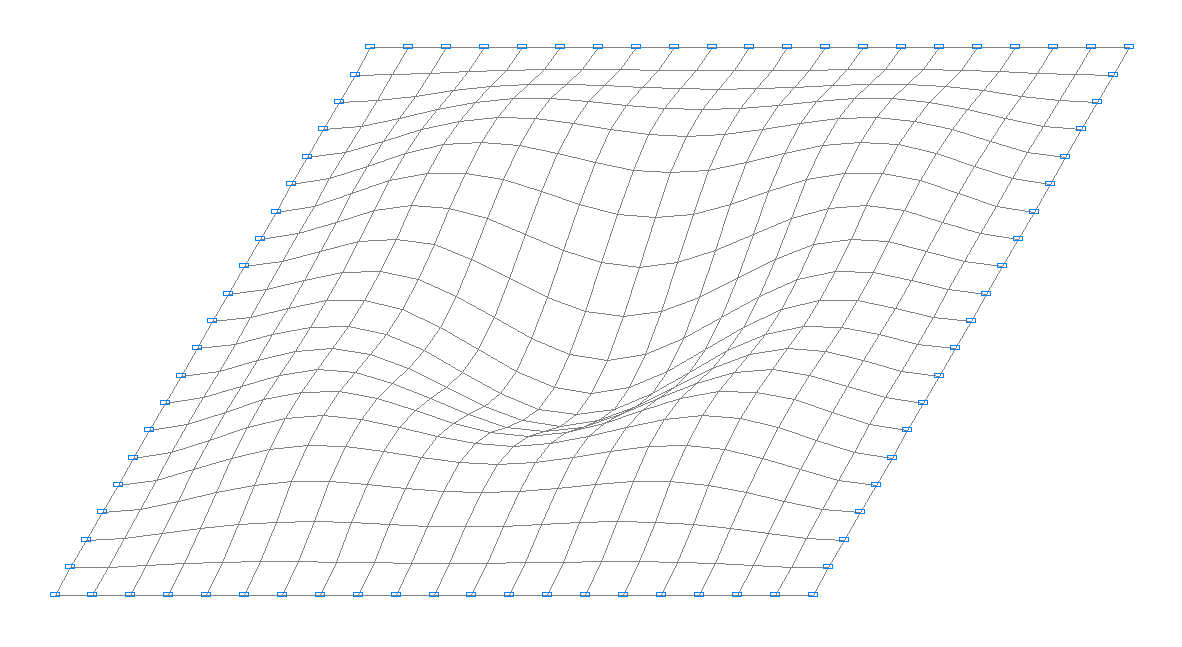
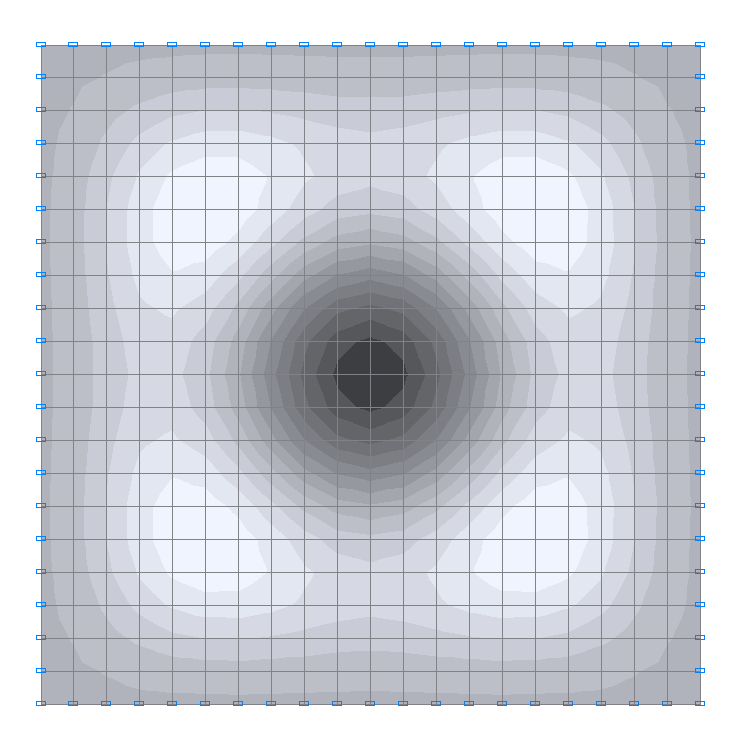
6-я собственная форма колебаний
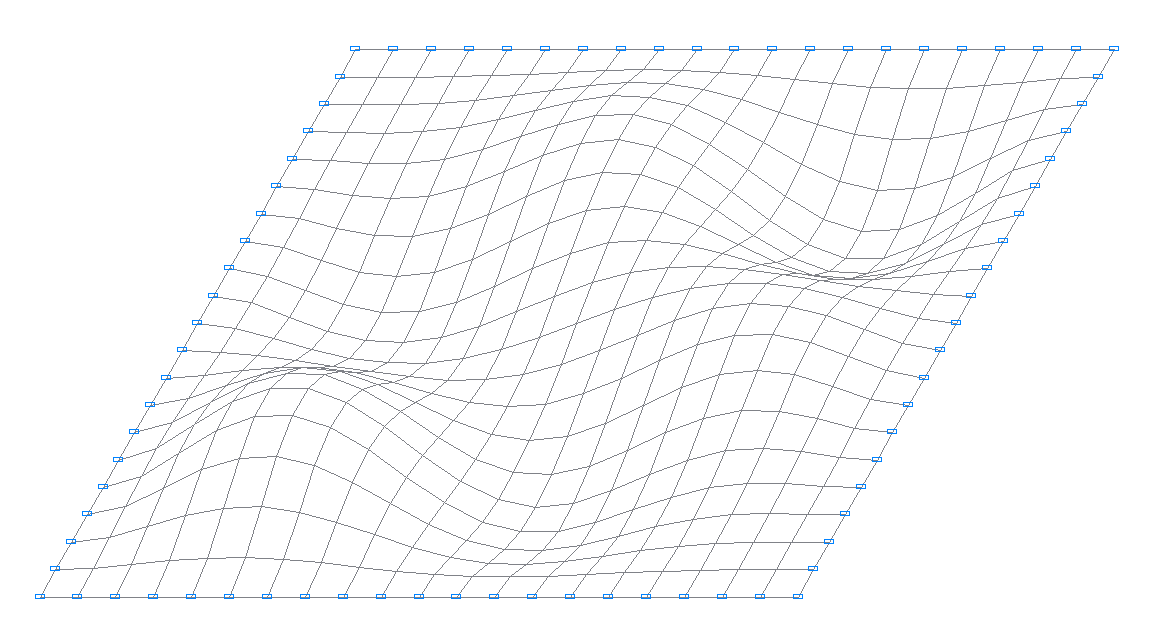


7-я собственная форма колебаний
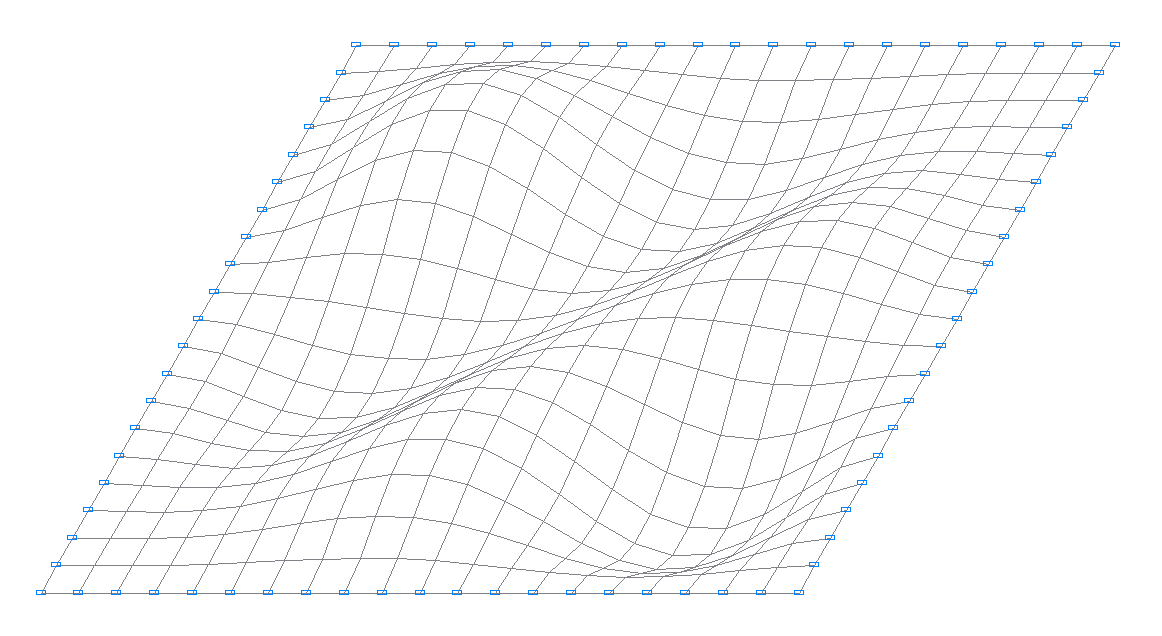
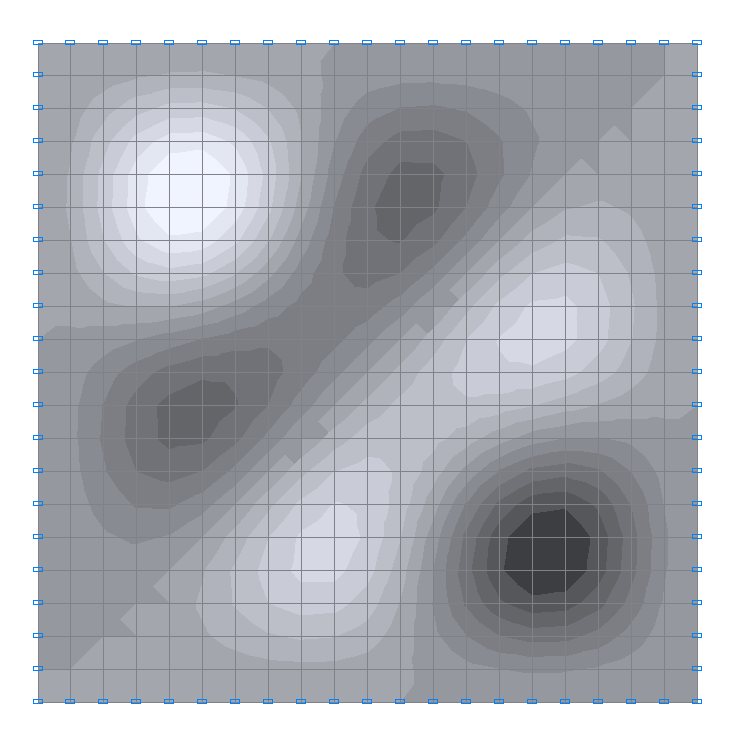

8-я собственная форма колебаний
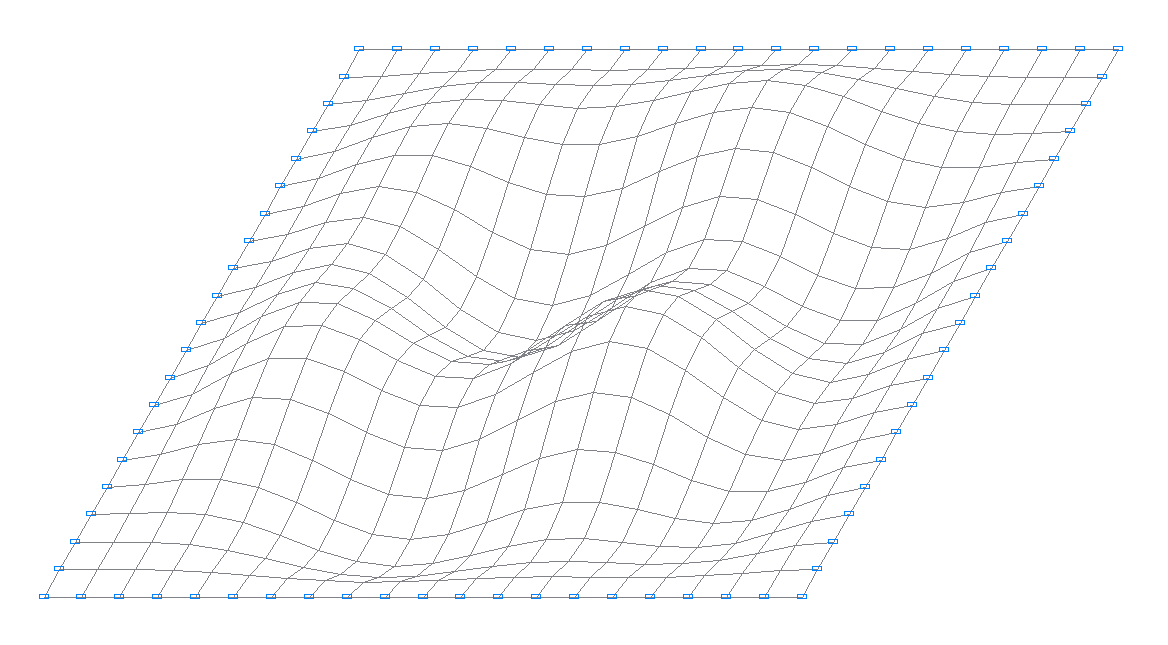


9-я собственная форма колебаний
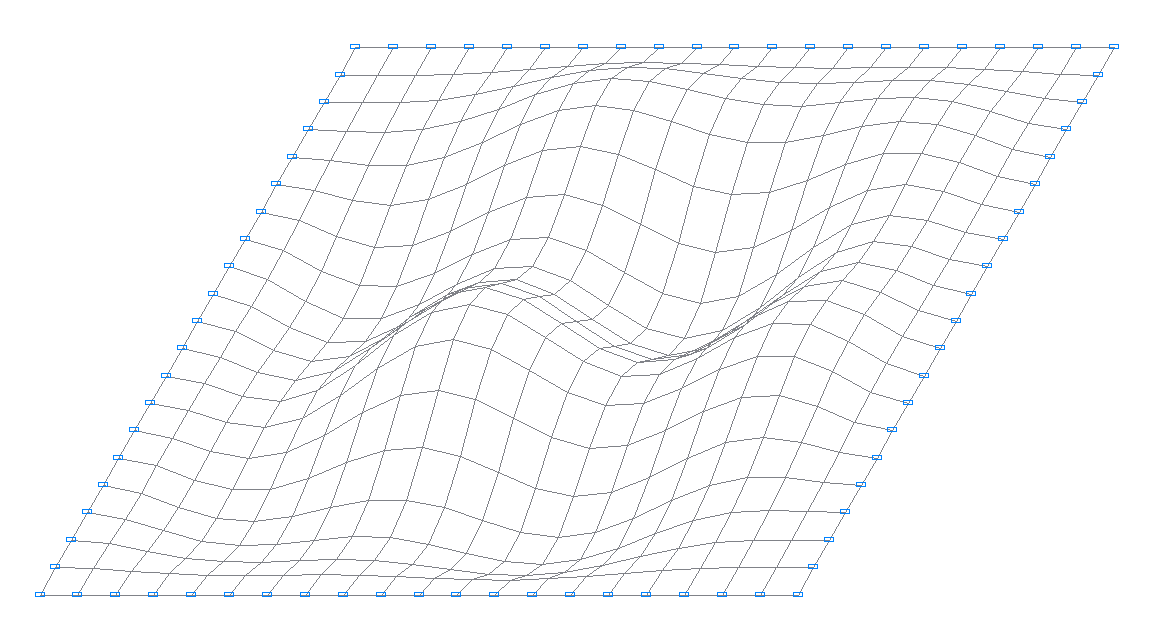


10-я собственная форма колебаний
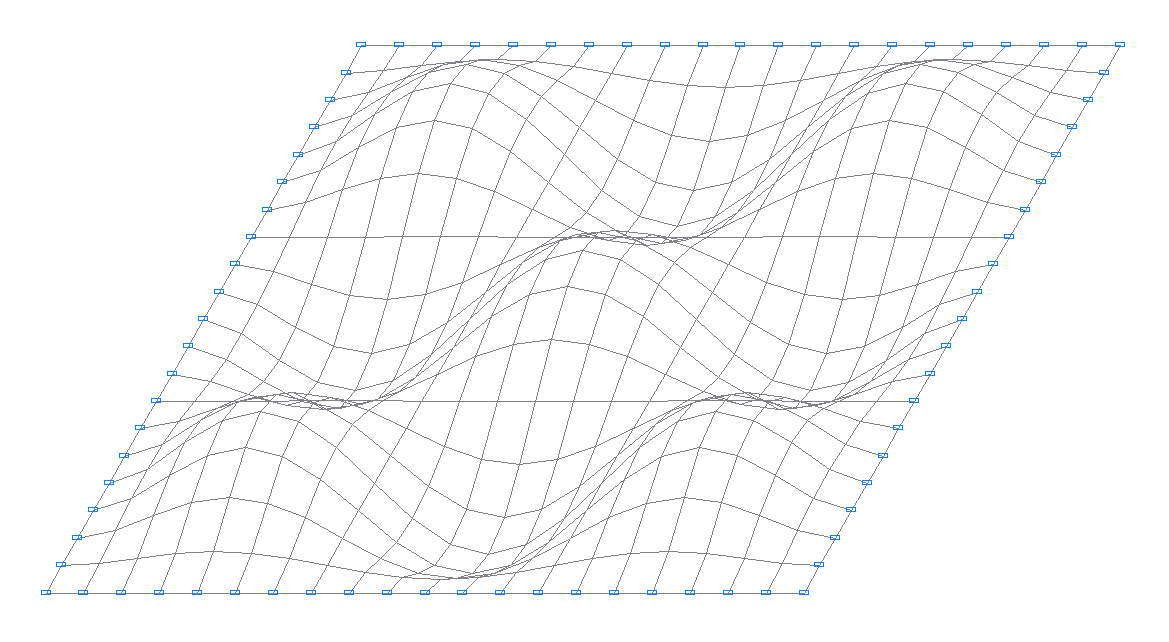


11-я собственная форма колебаний



12-я собственная форма колебаний
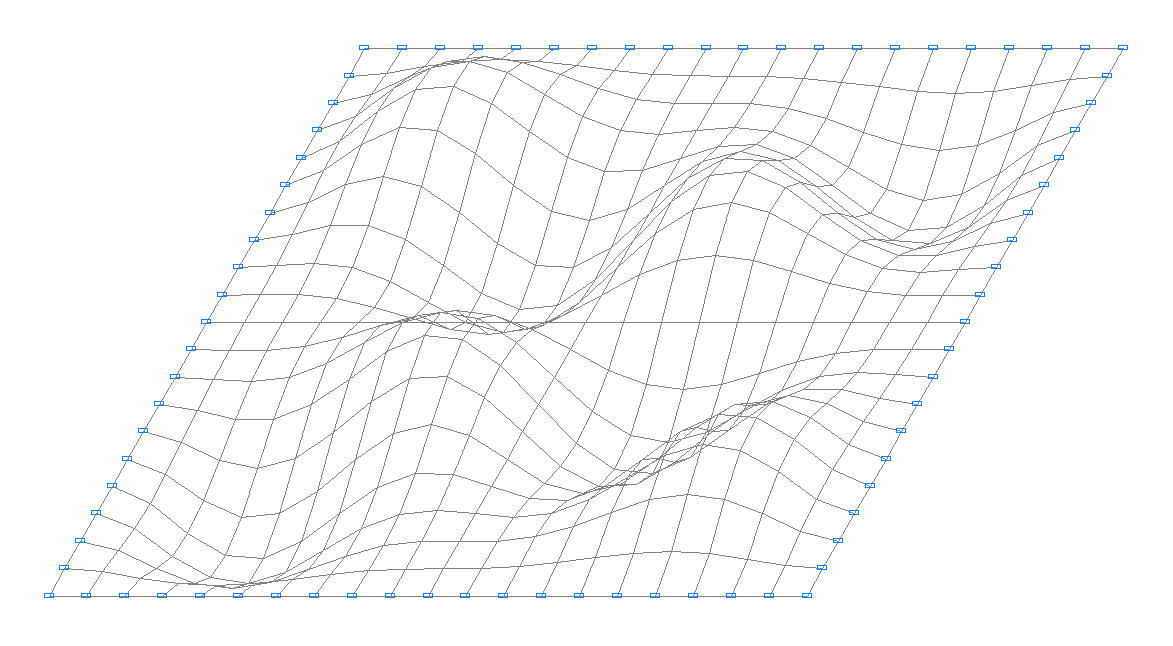


13-я собственная форма колебаний
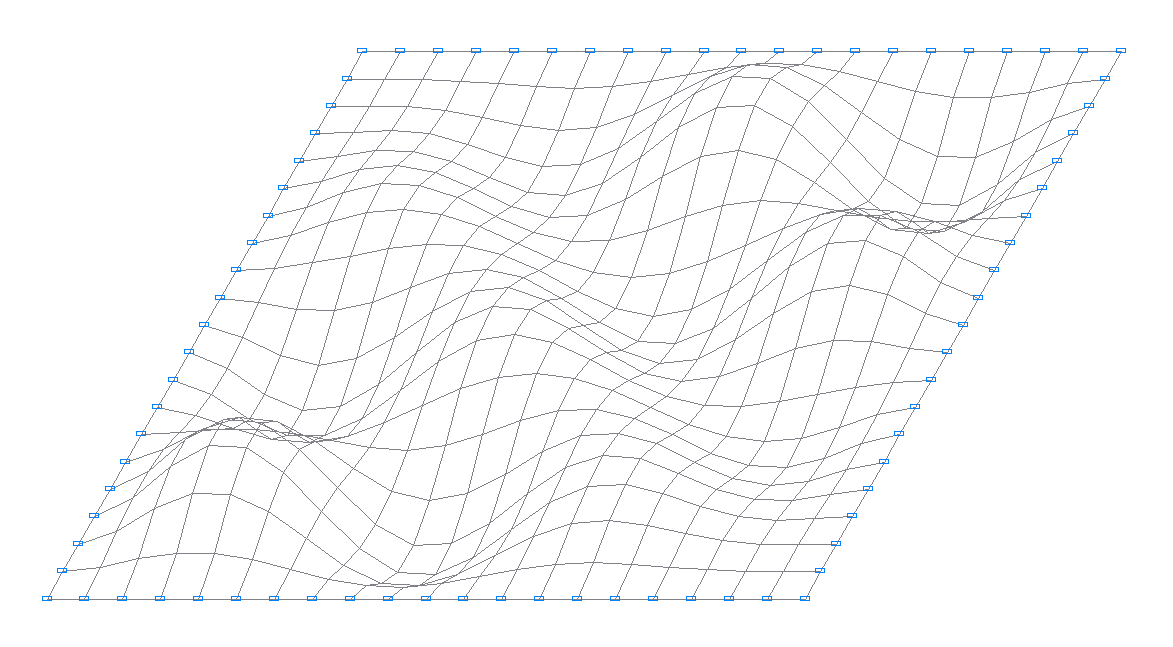


14-я собственная форма колебаний
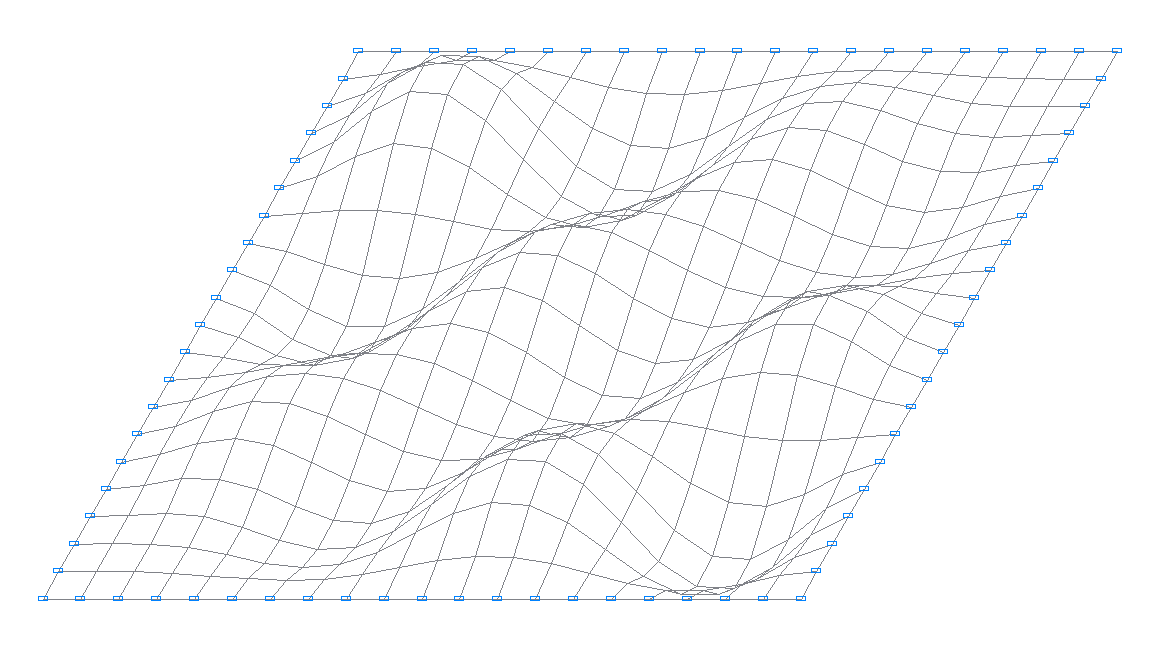


15-я собственная форма колебаний
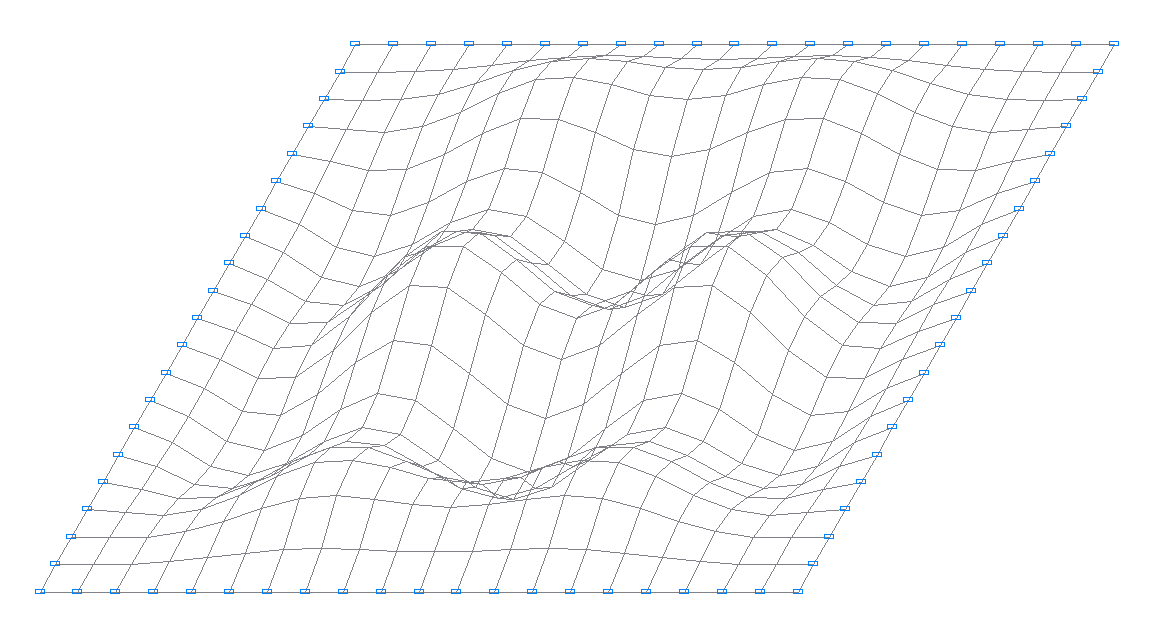


16-я собственная форма колебаний
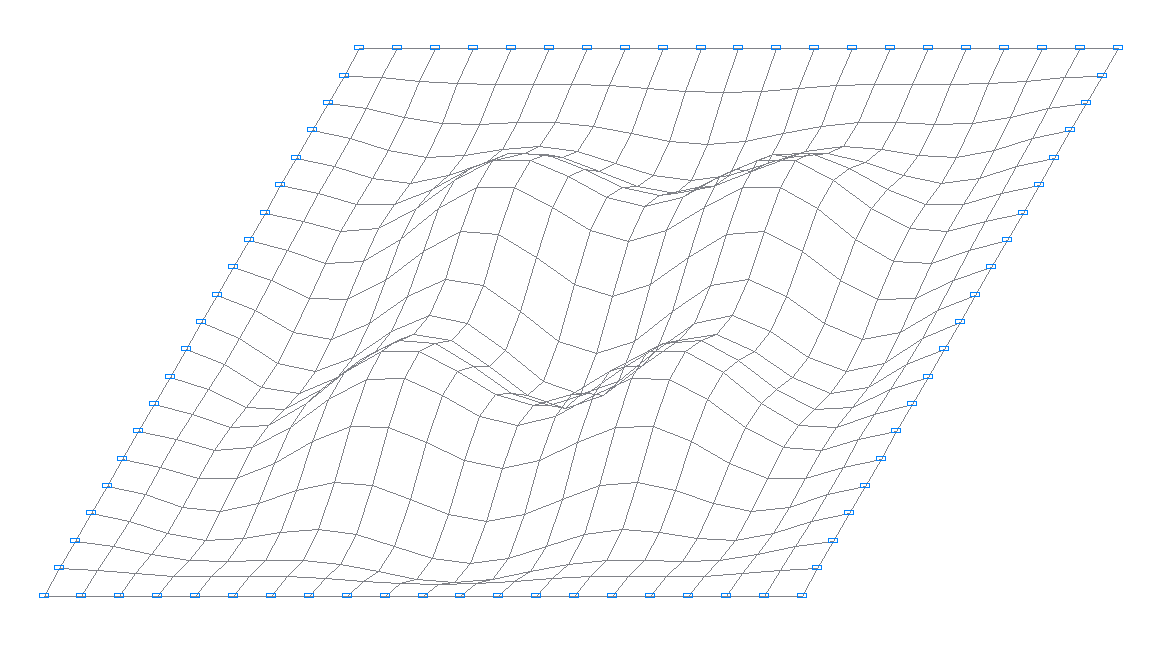


17-я собственная форма колебаний
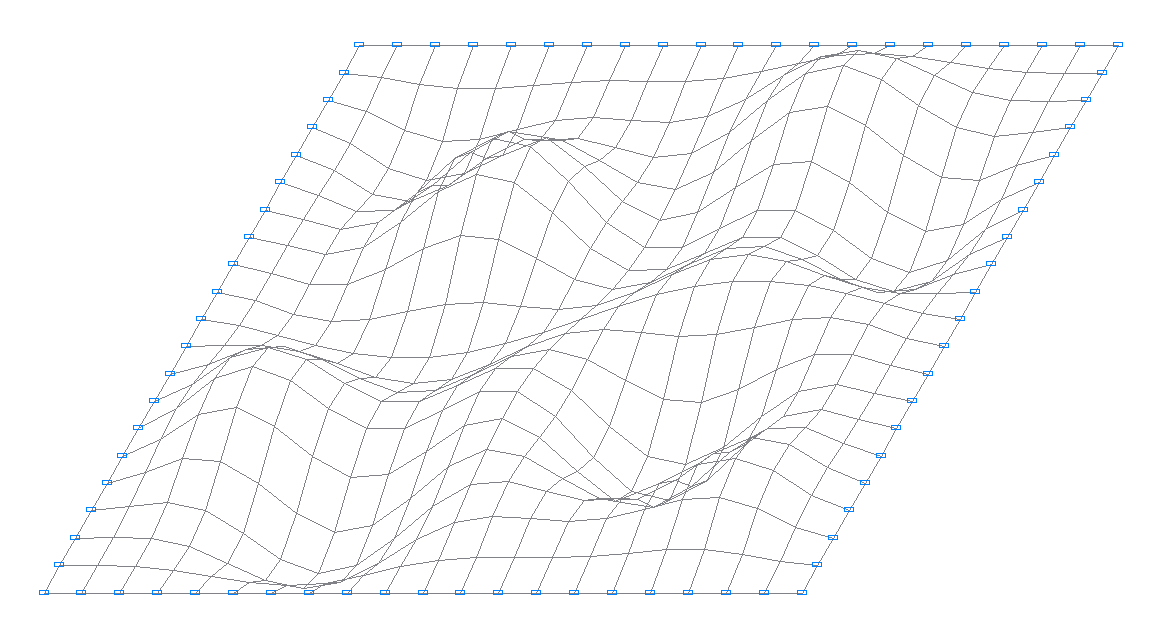


18-я собственная форма колебаний
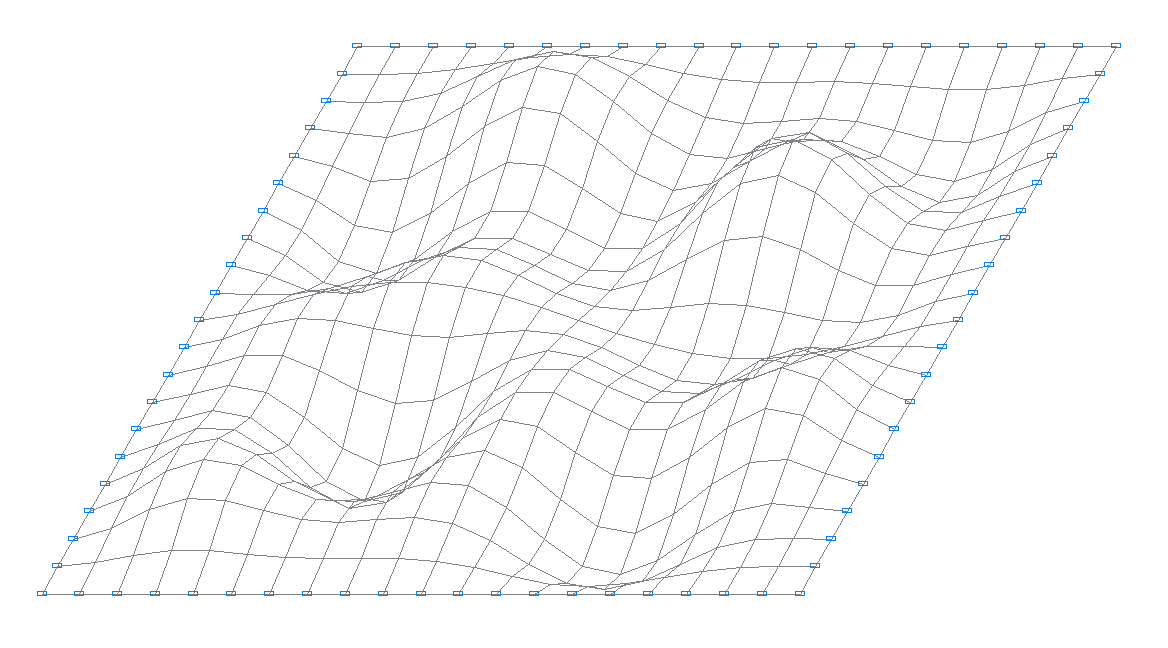


19-я собственная форма колебаний
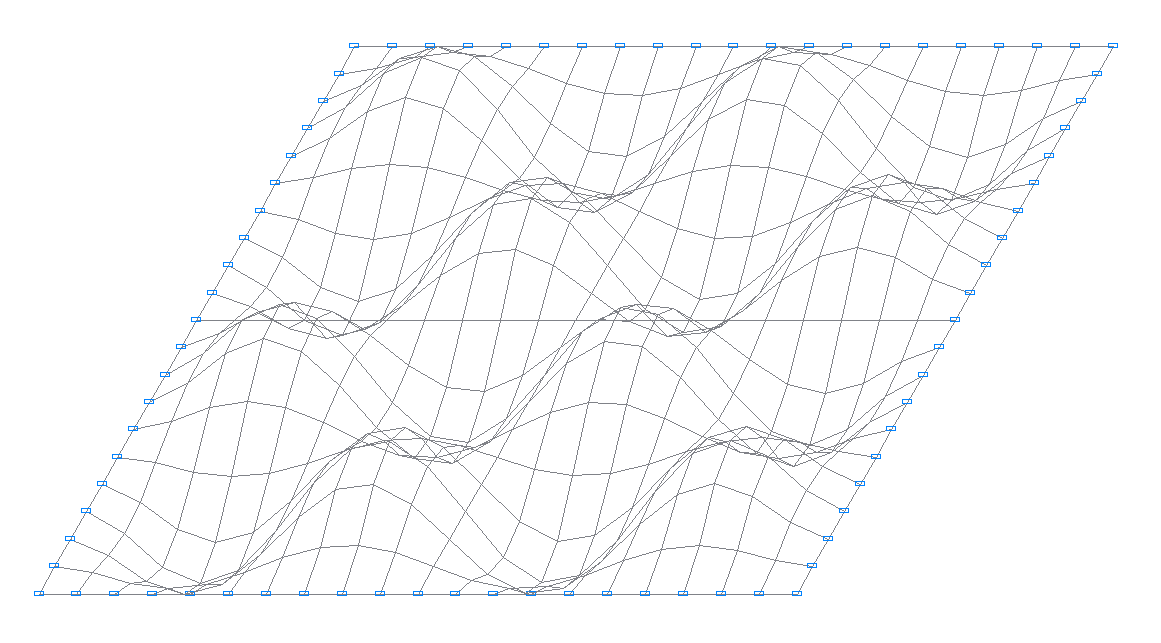


20-я собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, рад / с
|
Форма колебаний |
Число полуволн m1, m2 |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1 |
1, 1 |
560.1 |
558.5 |
0.29 |
|
2 |
1, 2 |
1143.2 |
1139.4 |
0.33 |
|
3 |
2, 1 |
1143.2 |
1139.4 |
0.33 |
|
4 |
2, 2 |
1686.6 |
1683.4 |
0.19 |
|
5 |
1, 3 |
2054.0 |
2042.8 |
0.55 |
|
6 |
3, 1 |
2054.0 |
2052.2 |
0.09 |
|
7 |
2, 3 |
2571.5 |
2569.1 |
0.09 |
|
8 |
3, 2 |
2571.5 |
2569.1 |
0.09 |
|
9 |
1, 4 |
3276.5 |
3267.5 |
0.27 |
|
10 |
4, 1 |
3276.5 |
3267.5 |
0.27 |
|
11 |
3, 3 |
3424.6 |
3434.5 |
0.29 |
|
12 |
2, 4 |
3782.2 |
3772.0 |
0.27 |
|
13 |
4, 2 |
3782.2 |
3786.2 |
0.11 |
|
14 |
3, 4 |
4611.8 |
4632.3 |
0.44 |
|
15 |
4, 3 |
4611.8 |
4632.3 |
0.44 |
|
16 |
1, 5 |
4806.6 |
4793.0 |
0.28 |
|
17 |
5, 1 |
4806.6 |
4796.7 |
0.21 |
|
18 |
2, 5 |
5307.4 |
5303.5 |
0.07 |
|
19 |
5, 2 |
5307.4 |
5303.5 |
0.07 |
|
20 |
4, 4 |
5774.8 |
5821.8 |
0.81 |
Замечания: При аналитическом решении собственные частоты колебаний ω квадратной защемленной по периметру пластины с плотностью материала ρ могут быть вычислены по следующей формуле, полученной на основе решения по методу Рэлея-Ритца:
\[\omega =\pi^{2}\cdot \left( {\frac{D}{\rho \cdot h}\cdot \left( {\frac{A_{m}^{4}}{a_{1}^{4}}+\frac{A_{n}^{4}}{a_{2}^{4}}+2\cdot \frac{B_{m} \cdot B_{n} }{a_{1}^{2}\cdot a_{2}^{2}}} \right)} \right)^{\frac{1}{2}}, \quad где: \] \[ A_{m} =\left\{ {{\begin{array}{*{20}c} {1.506} & {m=1} \\ {m+0.5} & {m\ge 2} \\ \end{array} }} \right., \quad A_{n} =\left\{ {{\begin{array}{*{20}c} {1.506} & {n=1} \\ {n+0.5} & {n\ge 2} \\ \end{array} }} \right., \quad B_{m} =\left\{ {{\begin{array}{*{20}c} {1.248} & {m=1} \\ {A_{m} \cdot \left( {A_{m} -\frac{2}{\pi }} \right)} & {m\ge 2} \\ \end{array} }} \right., \quad B_{m} =\left\{ {{\begin{array}{*{20}c} {1.248} & {n=1} \\ {A_{n} \cdot \left( {A_{n} -\frac{2}{\pi }} \right)} & {n\ge 2} \\ \end{array} }} \right., \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad m_{1} ,m_{2} =1,2,3, ... \]
