Свободные колебания круговой цилиндрической оболочки, свободно опертой по торцам
Цель: Модальный анализ круговой цилиндрической оболочки, свободно опертой по торцам.
Файл с исходными данными: 5.8_s.spr
Формулировка задачи: Определить собственные формы и частоты колебаний ω круговой цилиндрической оболочки, свободно опертой по торцам, с плотностью материала ρ.
Ссылки: И. А. Биргер, Я. Г. Пановко, Прочность, устойчивость, колебания, Справочник в трех томах, Том 3, Москва, Машиностроение, 1968, стр. 426.
В. Л. Бидерман, Теория механических колебаний, Москва, Высшая школа, 1980, стр. 290.
Исходные данные:
| E = 1.96·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 7.70 т/м3 | - плотность материала; |
| h = 0.25·10-3 м | - толщина цилиндрической оболочки; |
| R = 0.076 м | - радиус срединной поверхности цилиндрической оболочки; |
| L = 0.305 м | - длина цилиндрической оболочки. |
Конечноэлементная модель: Расчетная схема – система общего вида, 6400 четырехузловых элементов оболочки типа 50. Сетка конечных элементов разбита с шагом 4.765625·10-3 м в меридиональном направлении (64 элемента) и с шагом 3.6º в окружном направлении (100 элементов). Обеспечение граничных условий на свободно опертых торцах достигается за счет наложения связей по направлениям линейных перемещений в их плоскости (степени свободы Y, Z). Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связей конечной жесткости (100 элементов типа 51) в узлах поперечного сечения плоскостью симметрии цилиндрической оболочки в меридиональном направлении (kx = 1.0 кН/м). Распределенная масса задается преобразованием статической нагрузки от собственного веса цилиндрической оболочки: ow = γ∙h, где γ = ρ∙g = 75.537 кН/м3. Количество узлов в расчетной схеме – 6500. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD
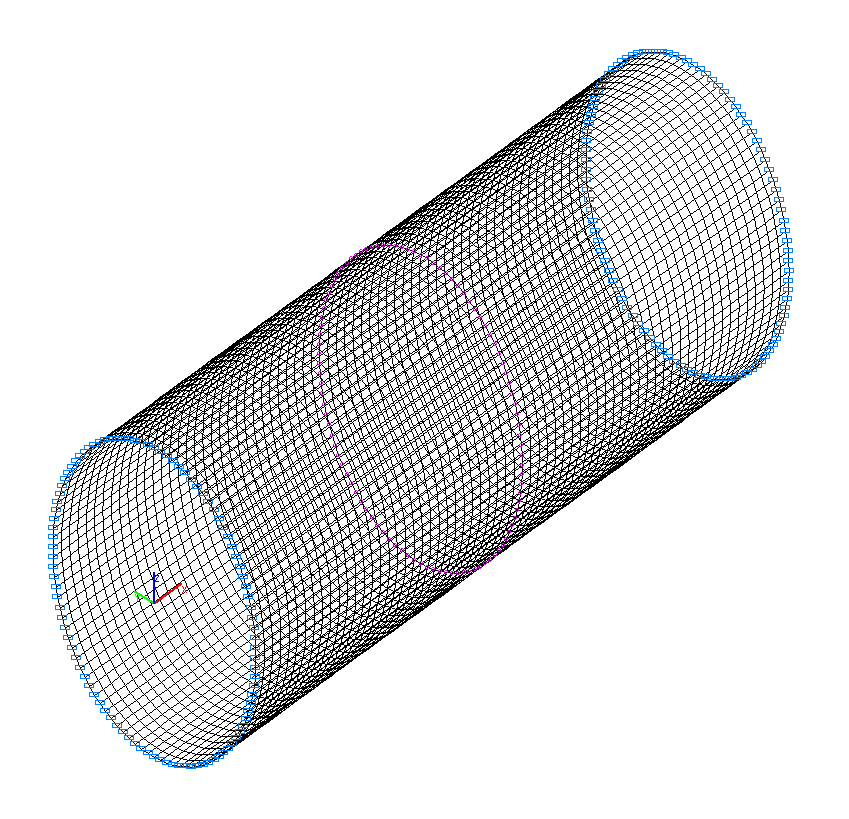
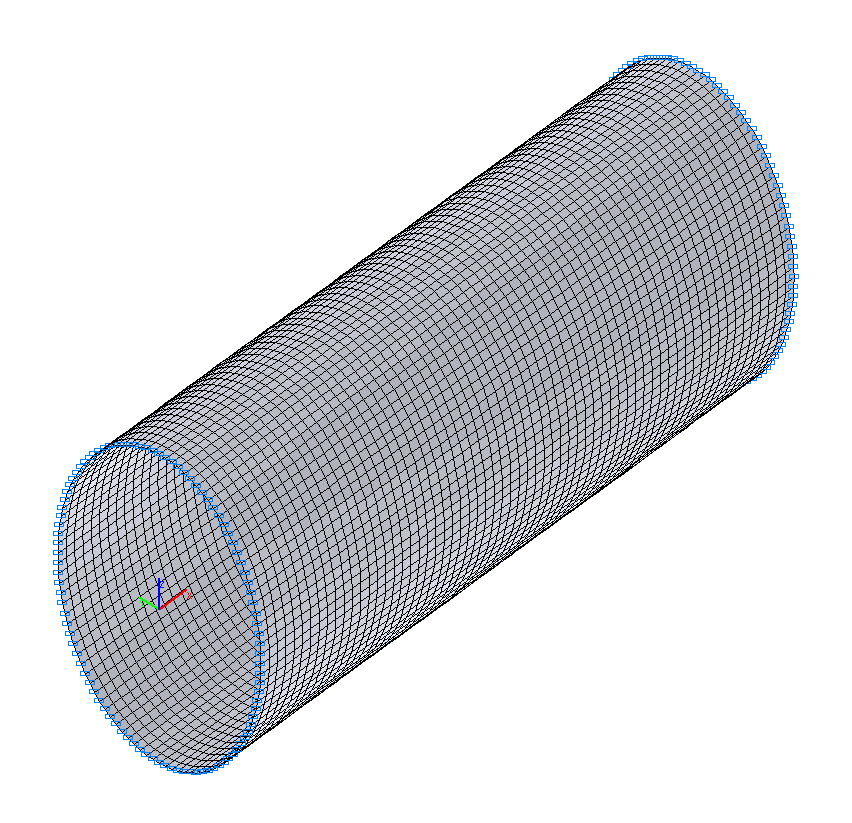
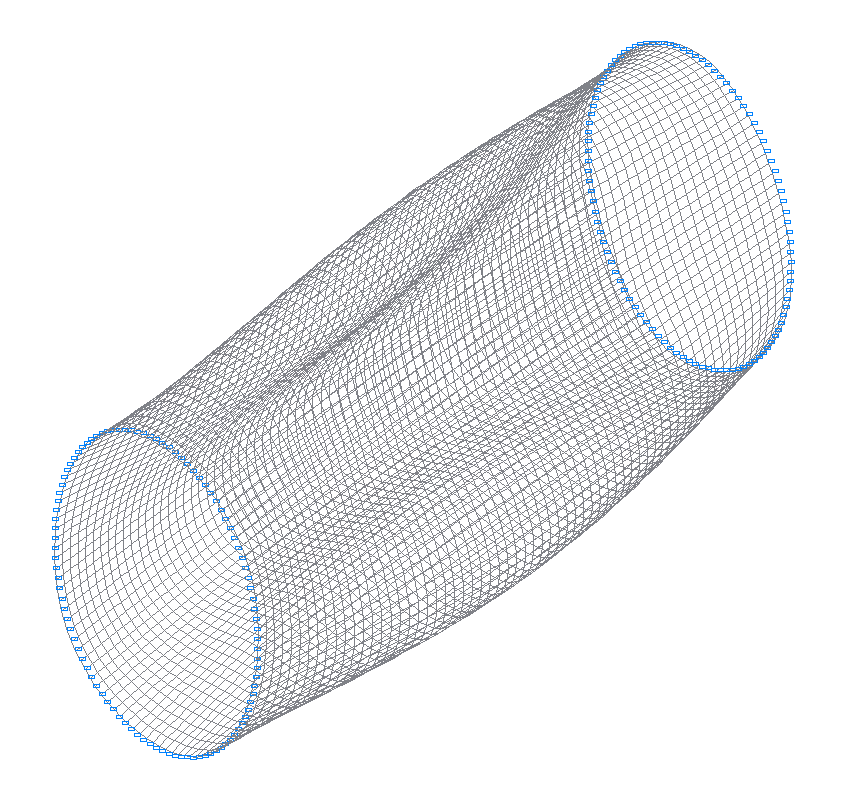
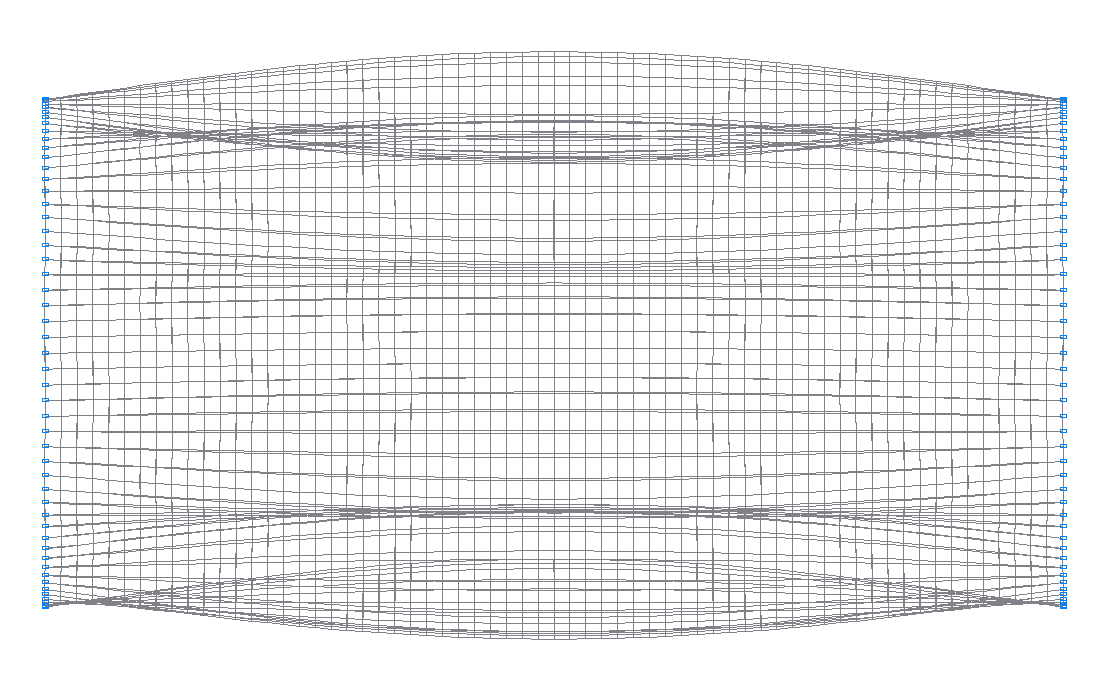
Расчетная схема
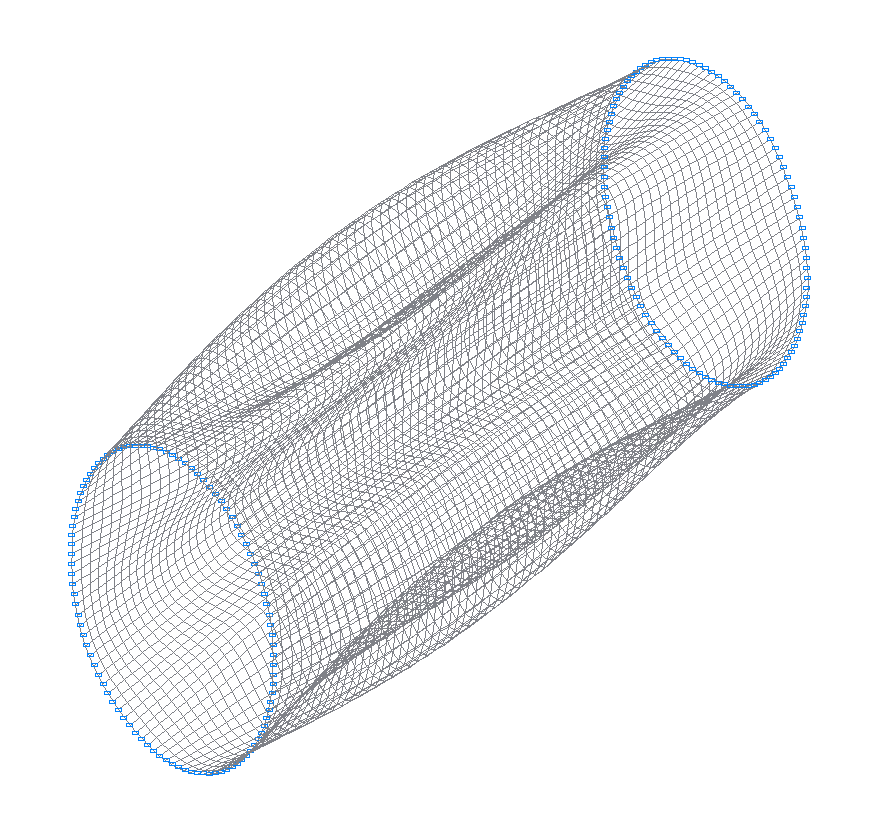


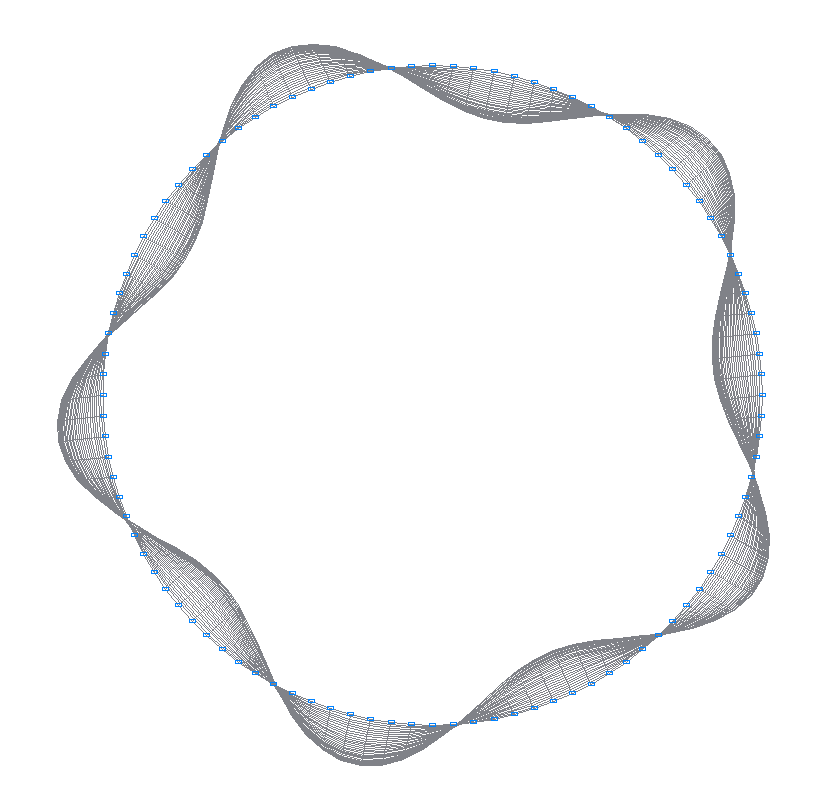
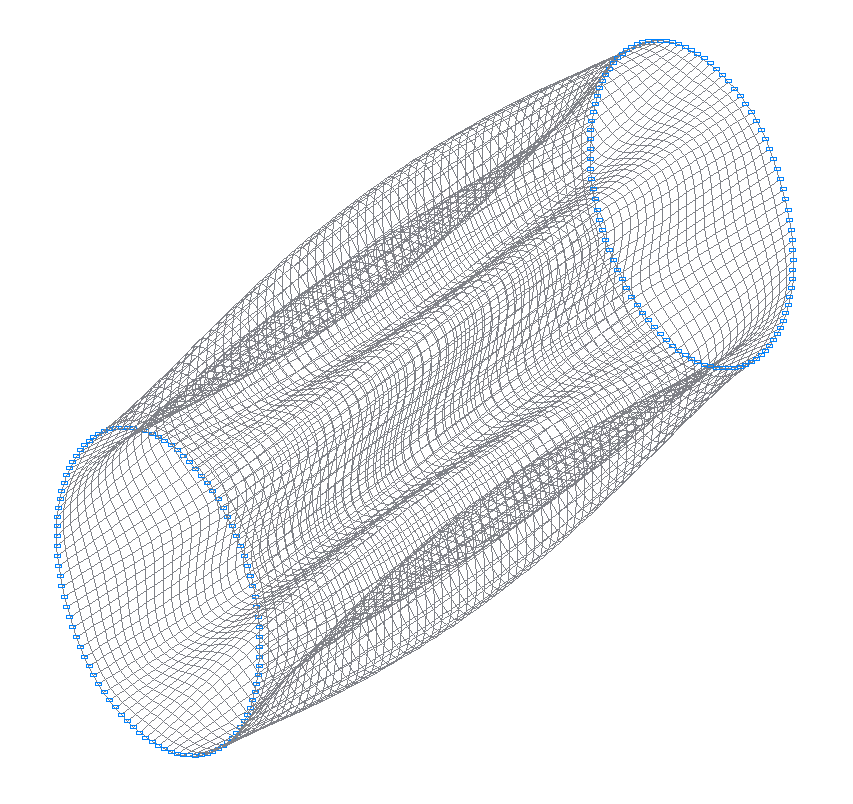
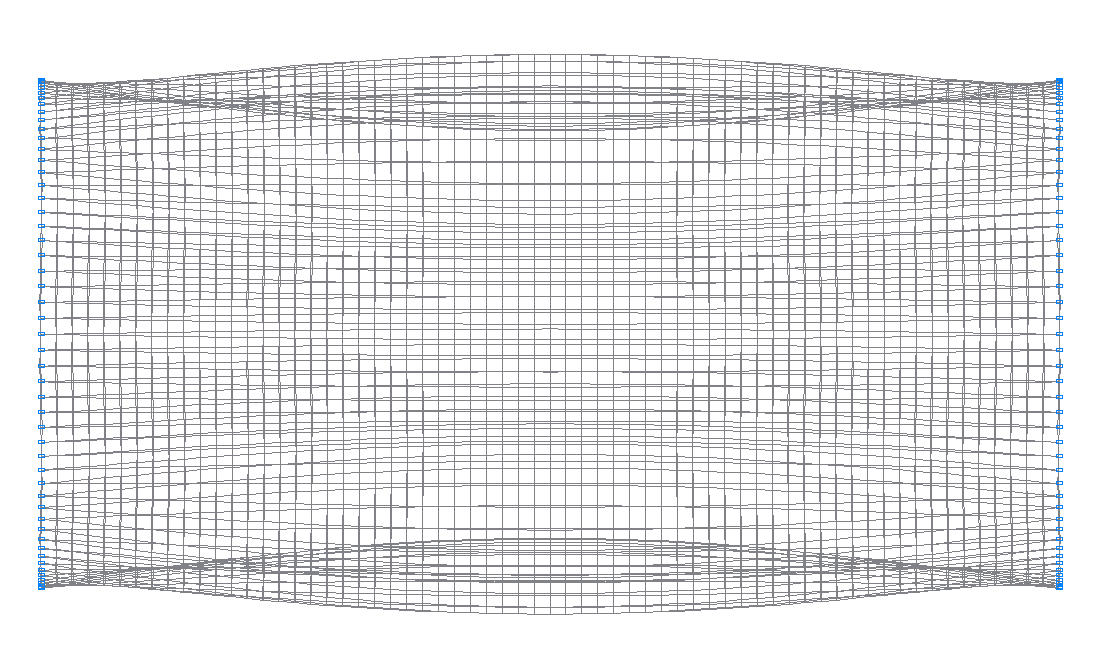
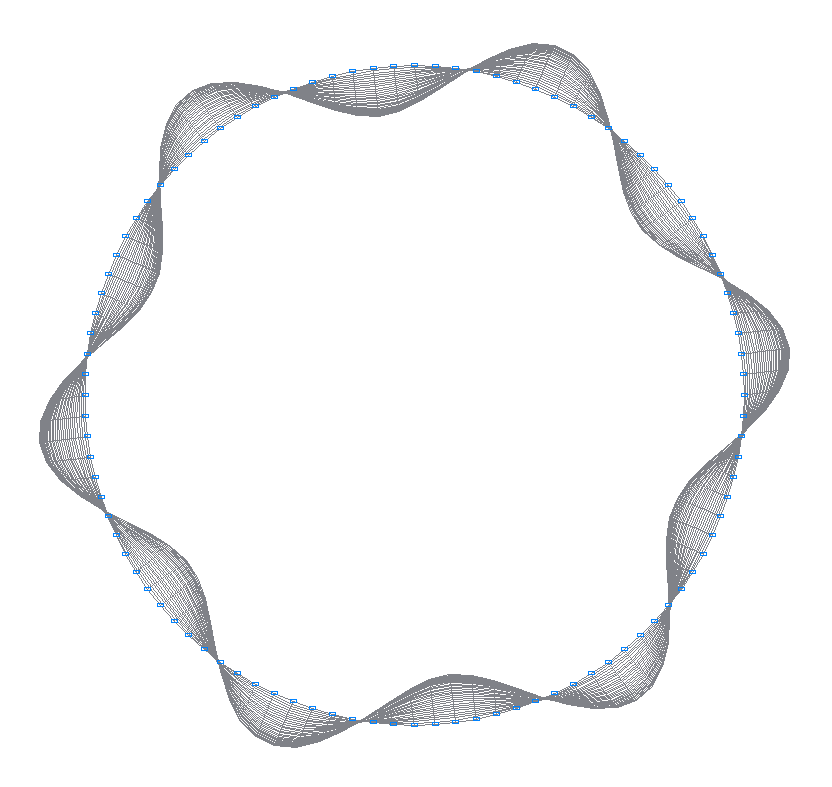
2-я (1-я теоретическая) собственная форма колебаний

4-я (3-я теоретическая) собственная форма колебаний
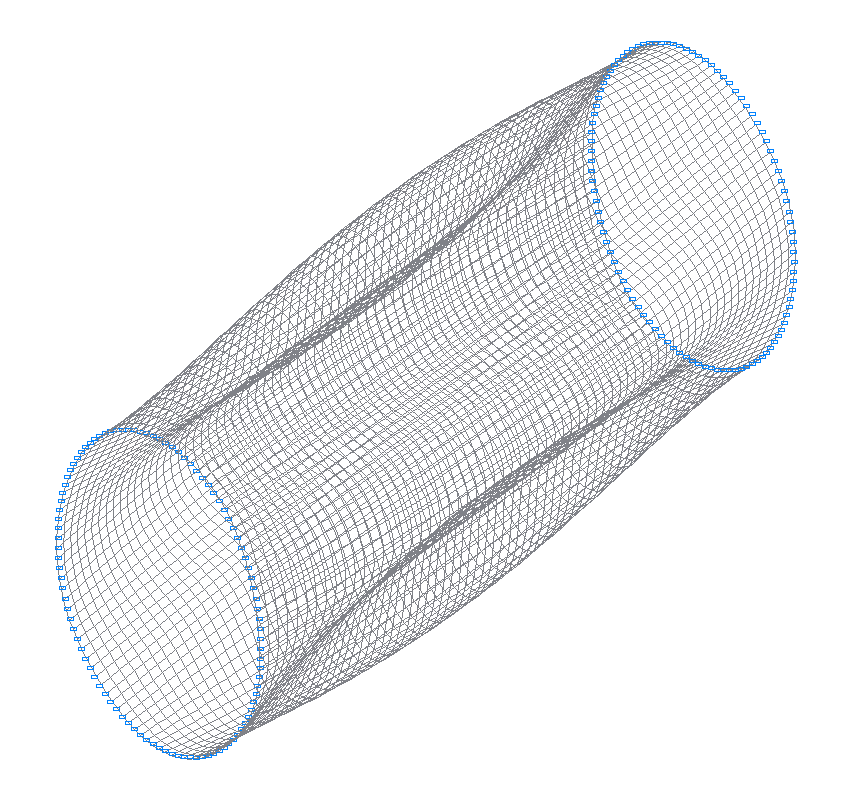

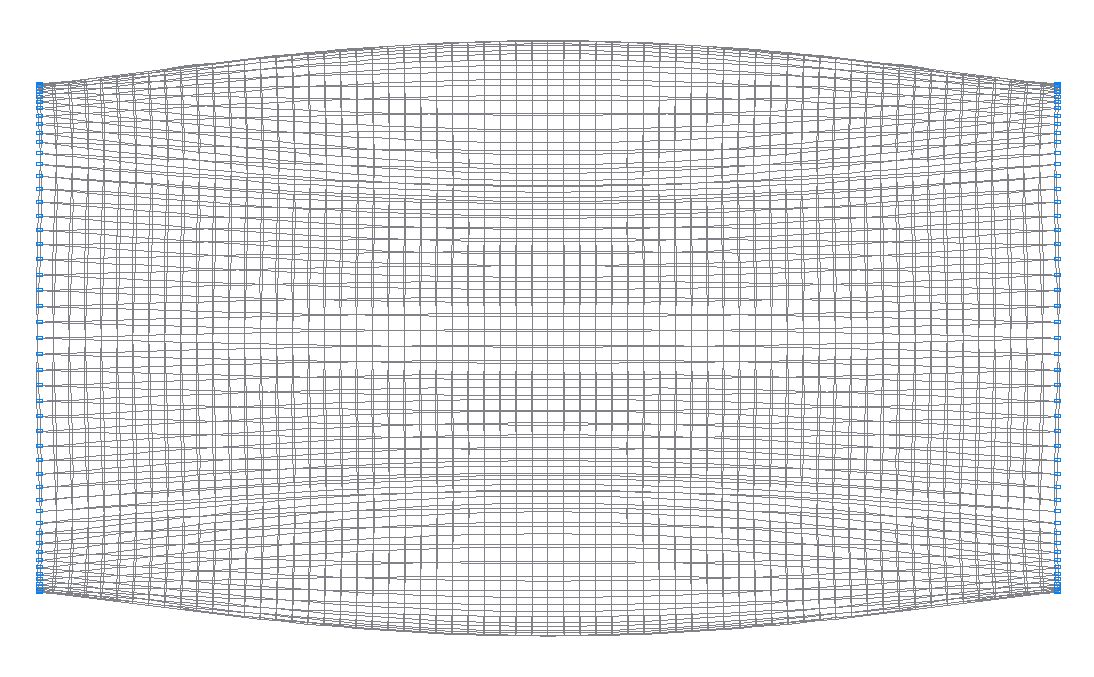

6-я (5-я теоретическая) собственная форма колебаний
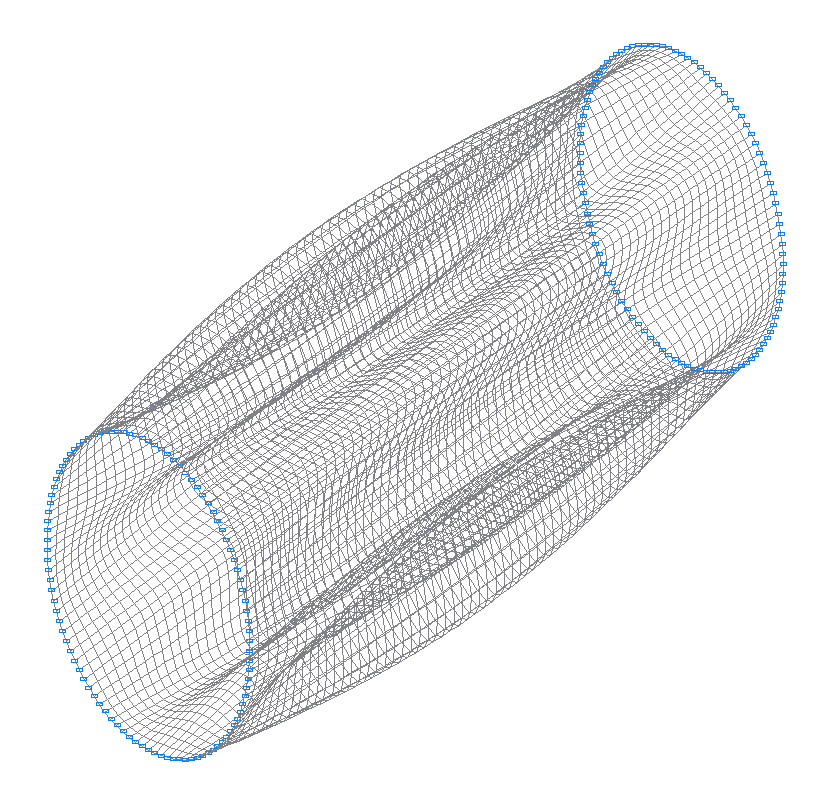

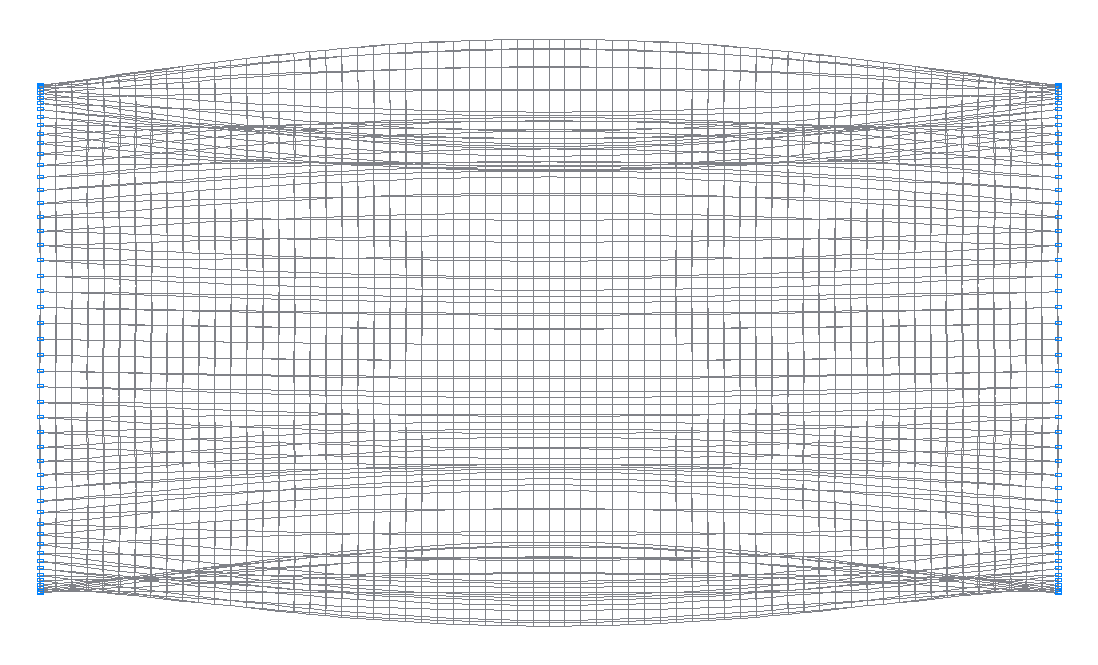
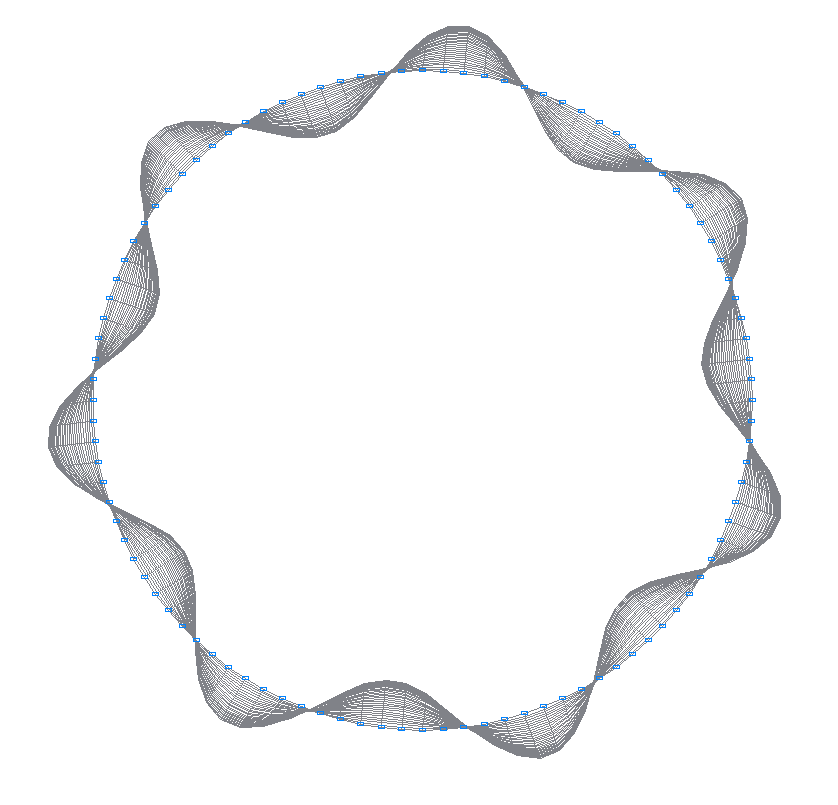
8-я (7-я теоретическая) собственная форма колебаний

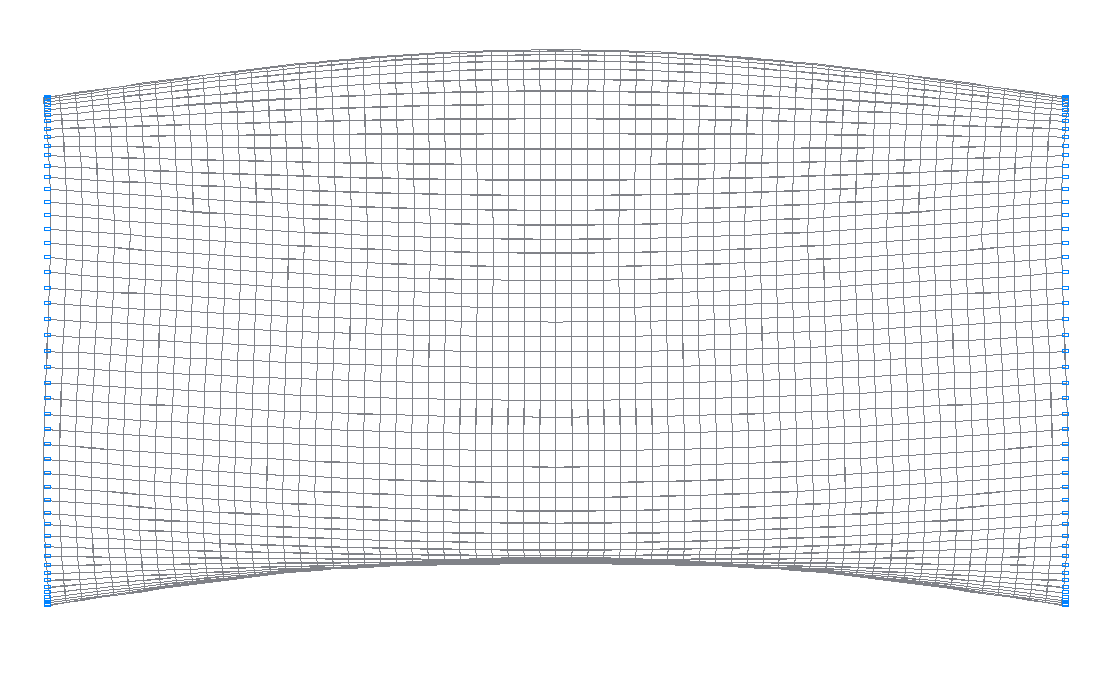
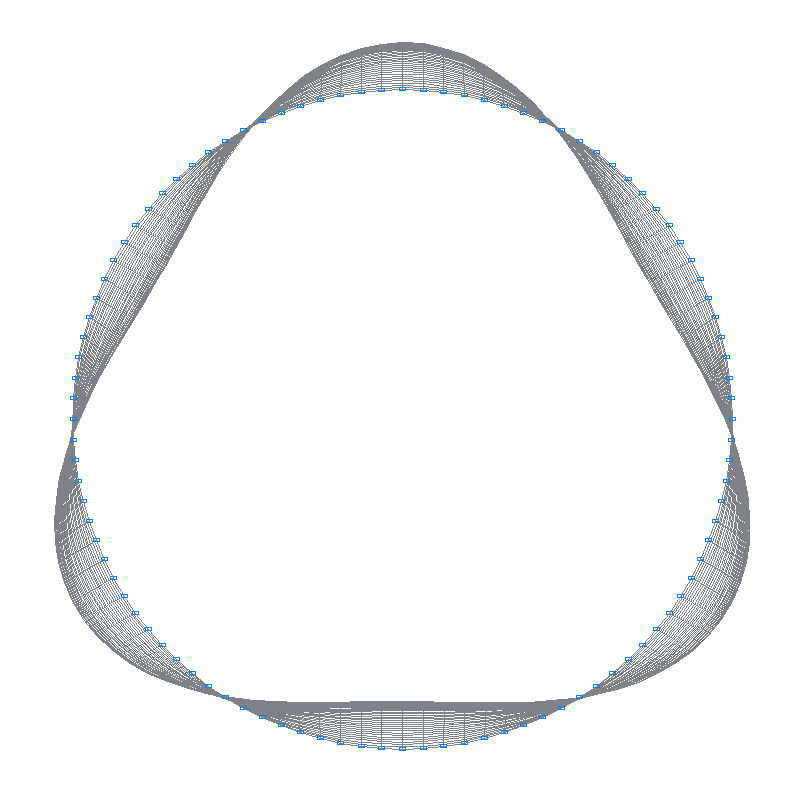
10-я (9-я теоретическая) собственная форма колебаний
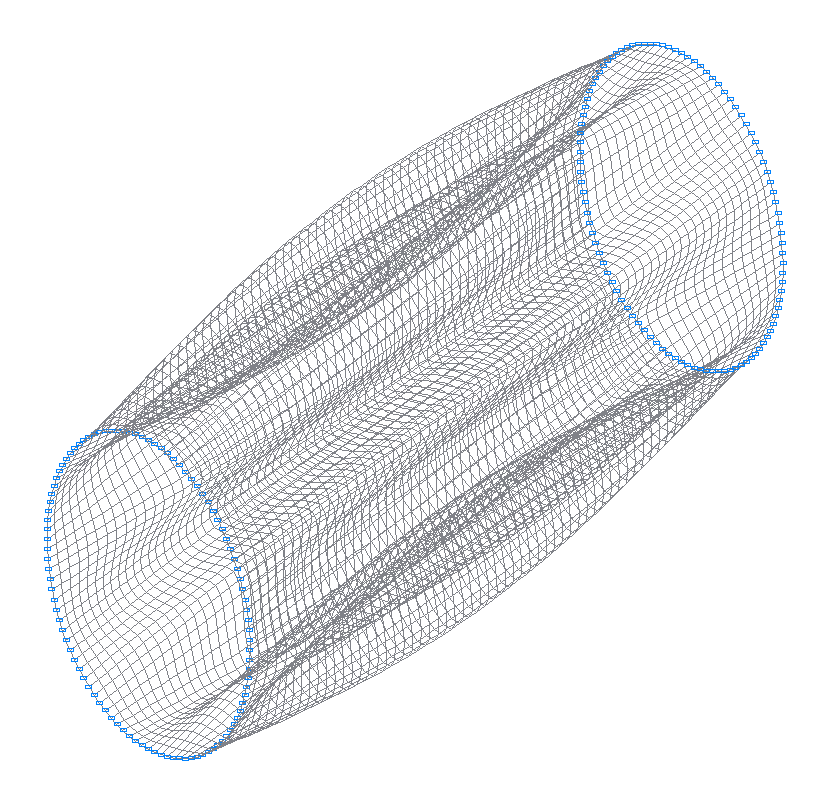

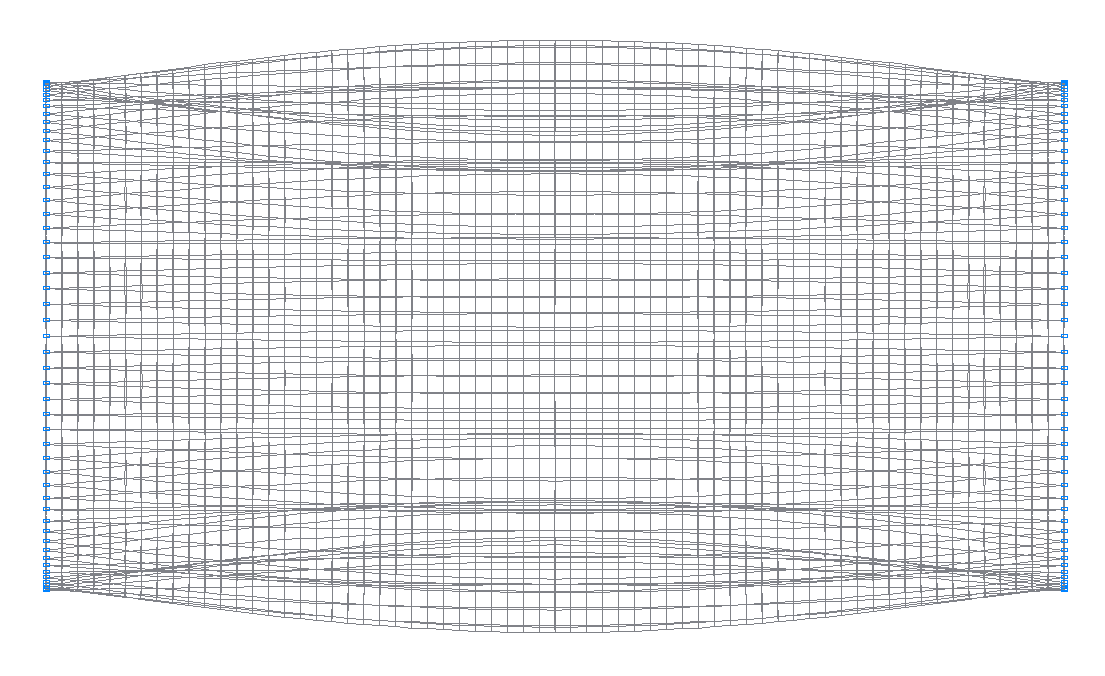
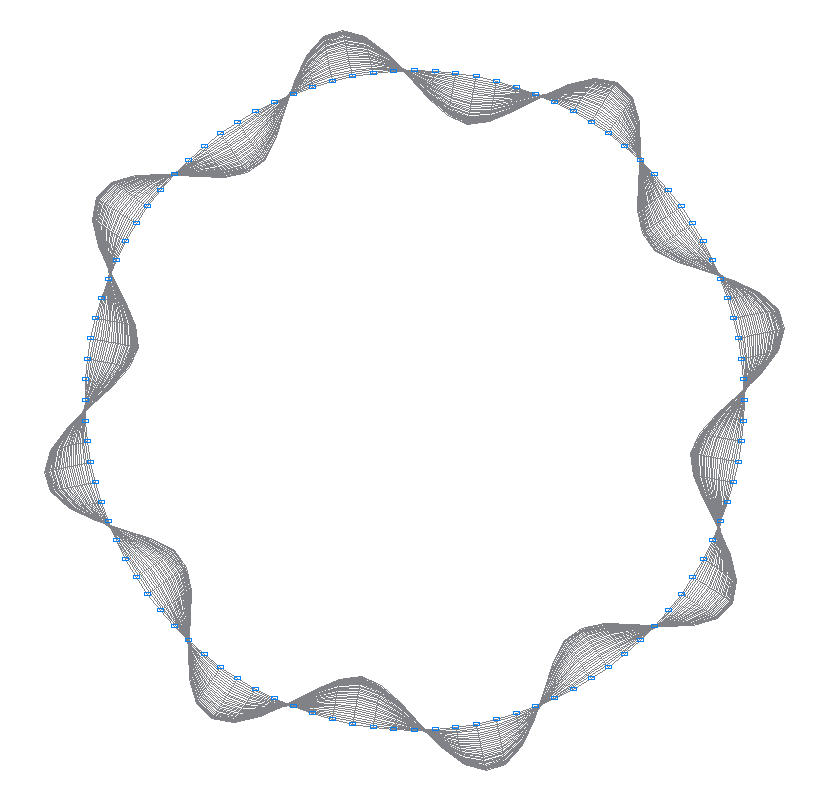
12-я (11-я теоретическая) собственная форма колебаний
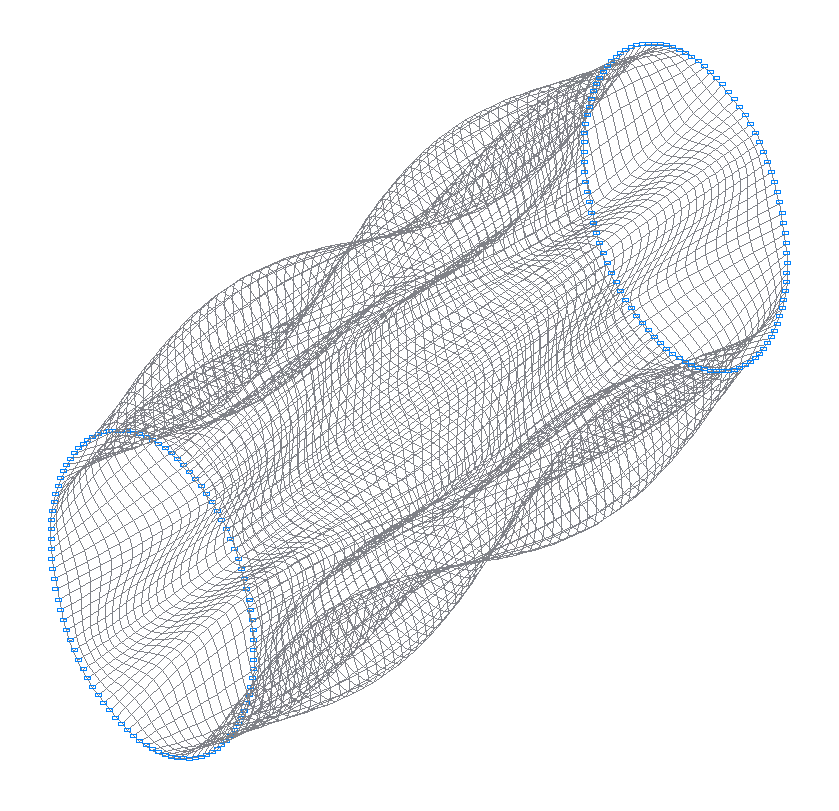


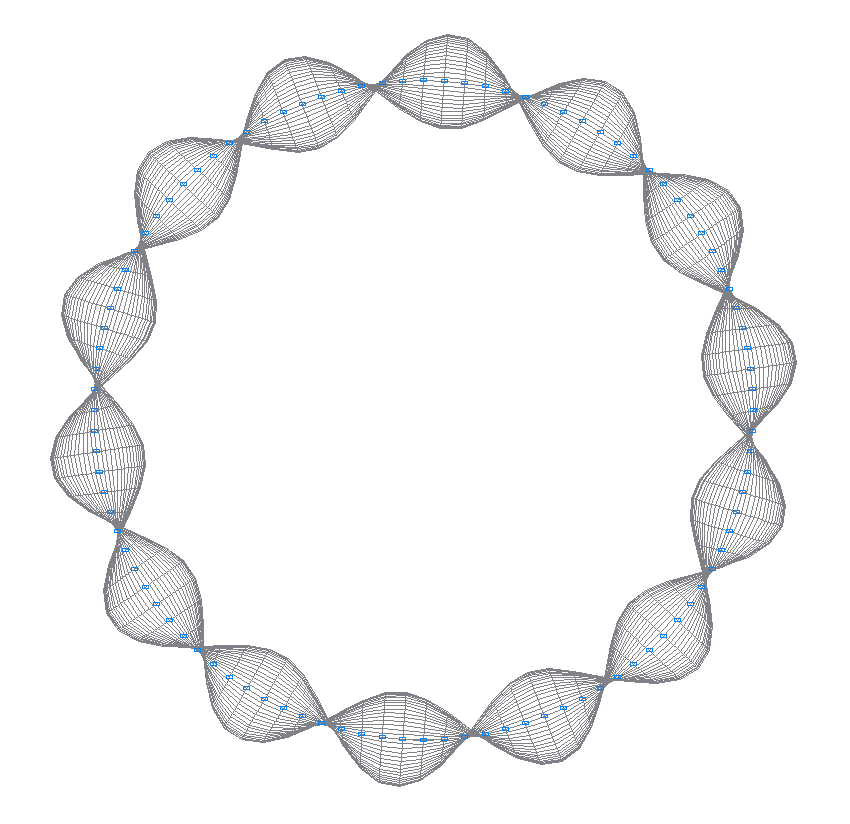
14-я (13-я теоретическая) собственная форма колебаний
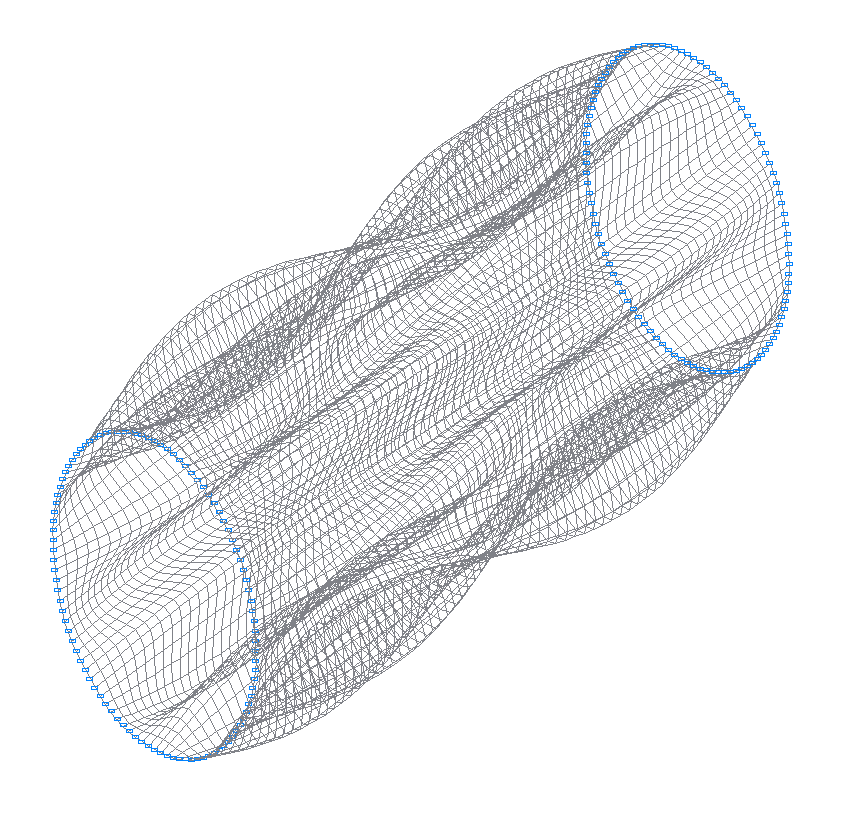
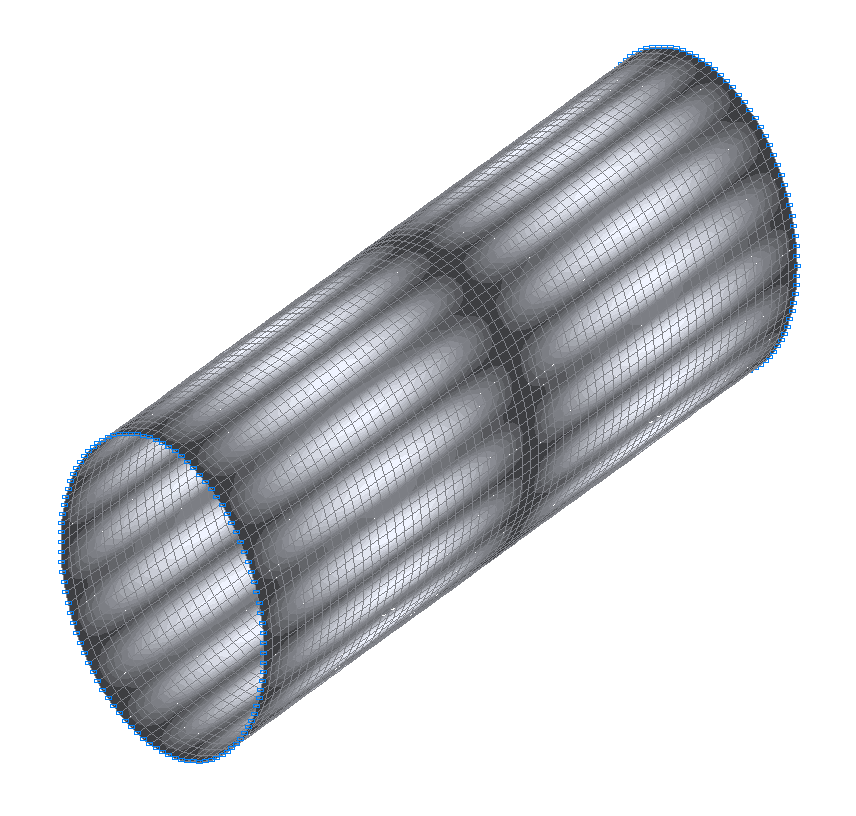


16-я (15-я теоретическая) собственная форма колебаний



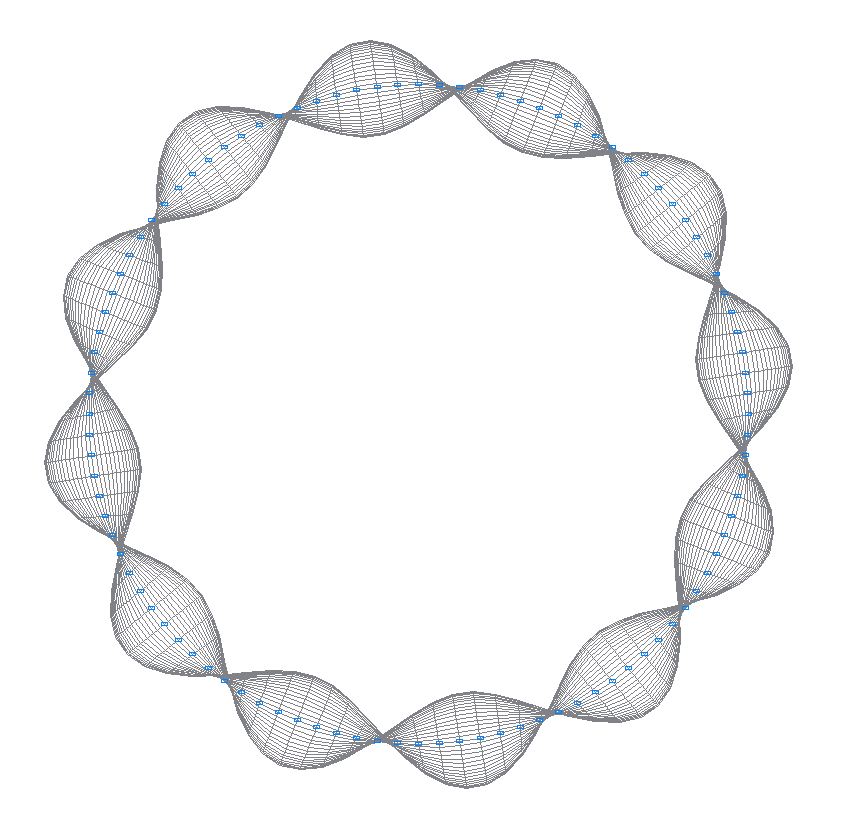
18-я (17-я теоретическая) собственная форма колебаний
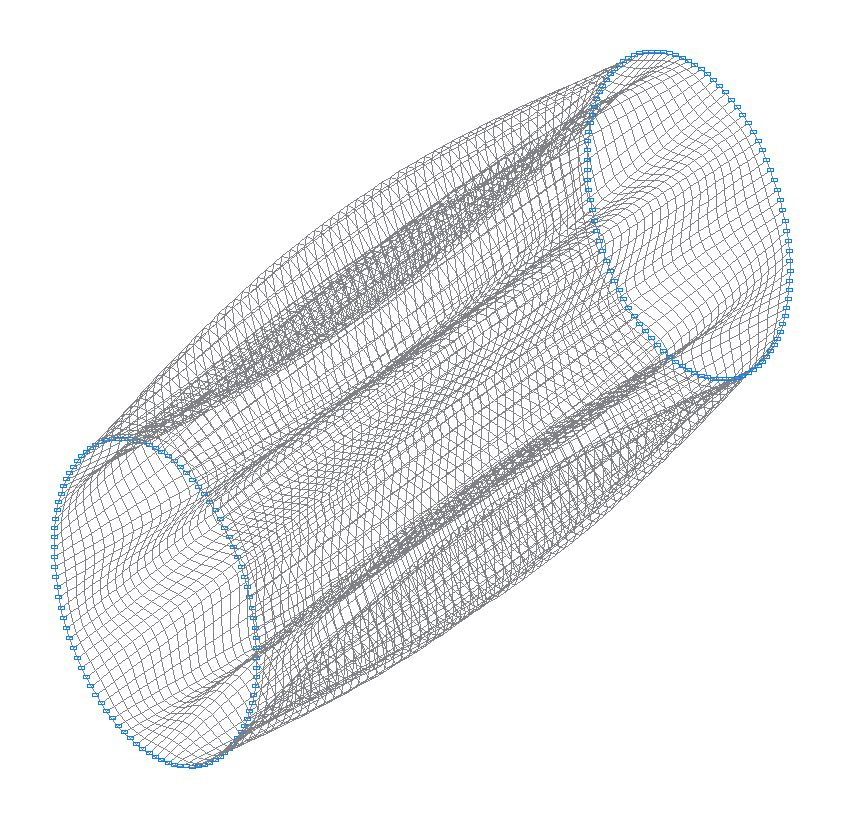

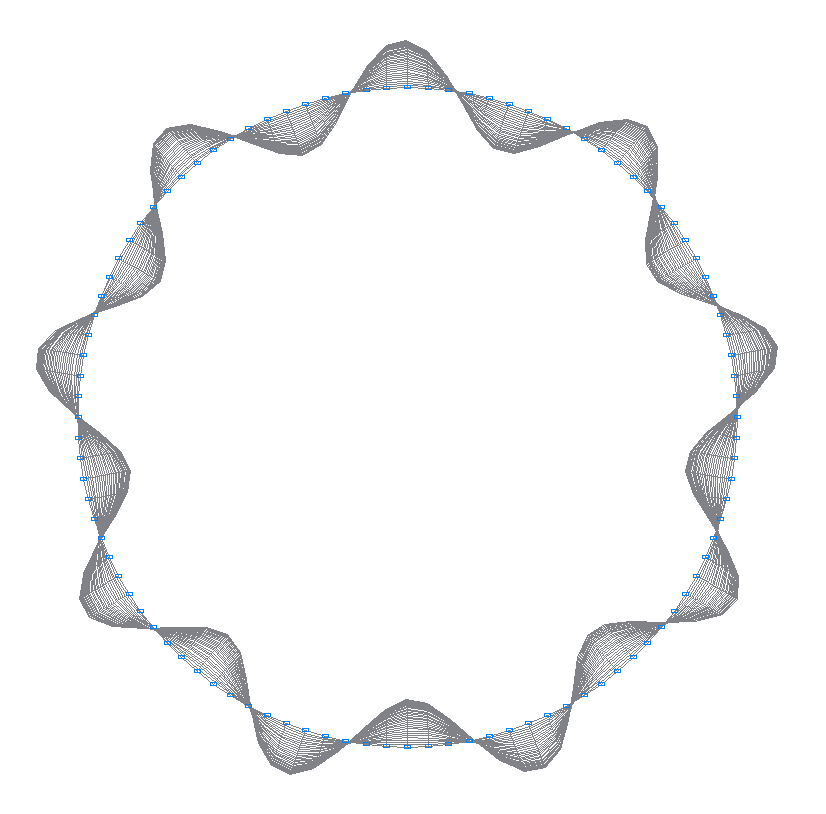
20-я (19-я теоретическая) собственная форма колебаний



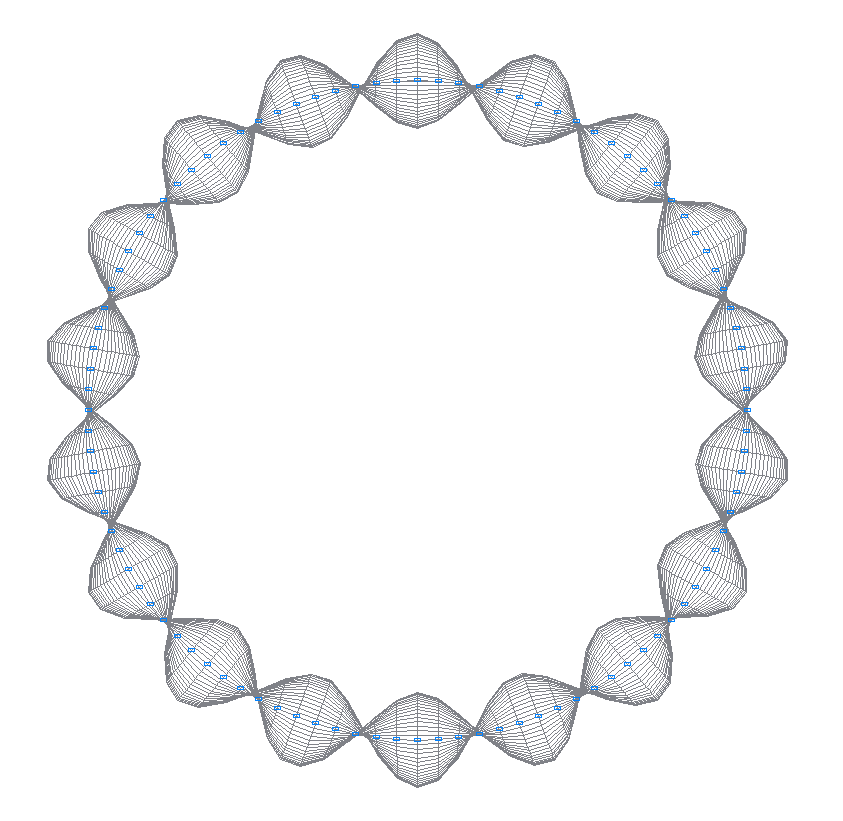
22-я (21-я теоретическая) собственная форма колебаний
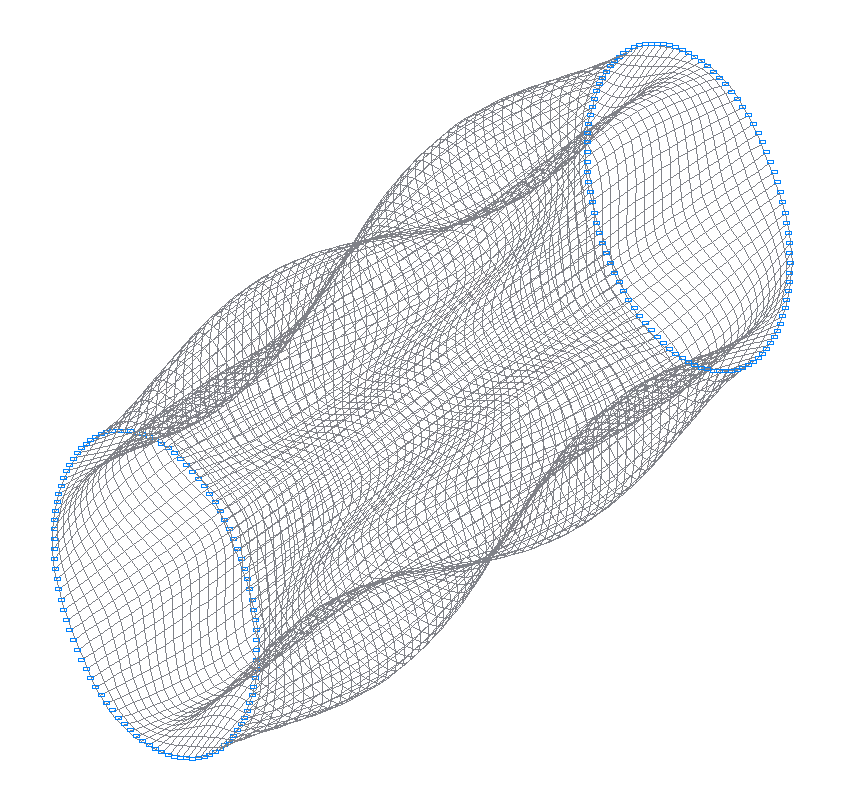
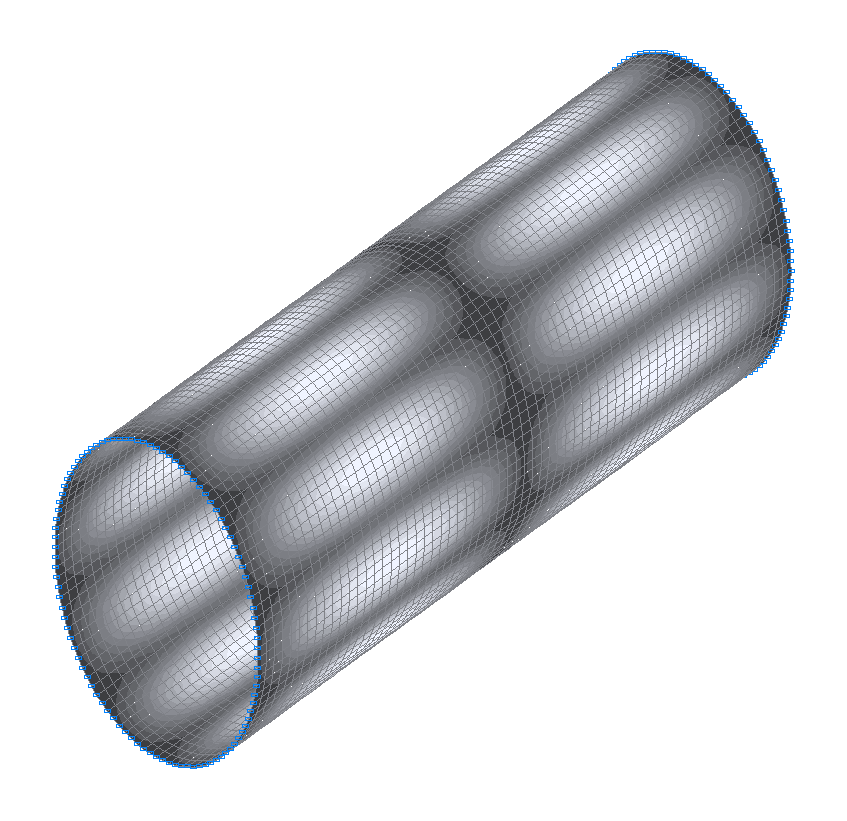
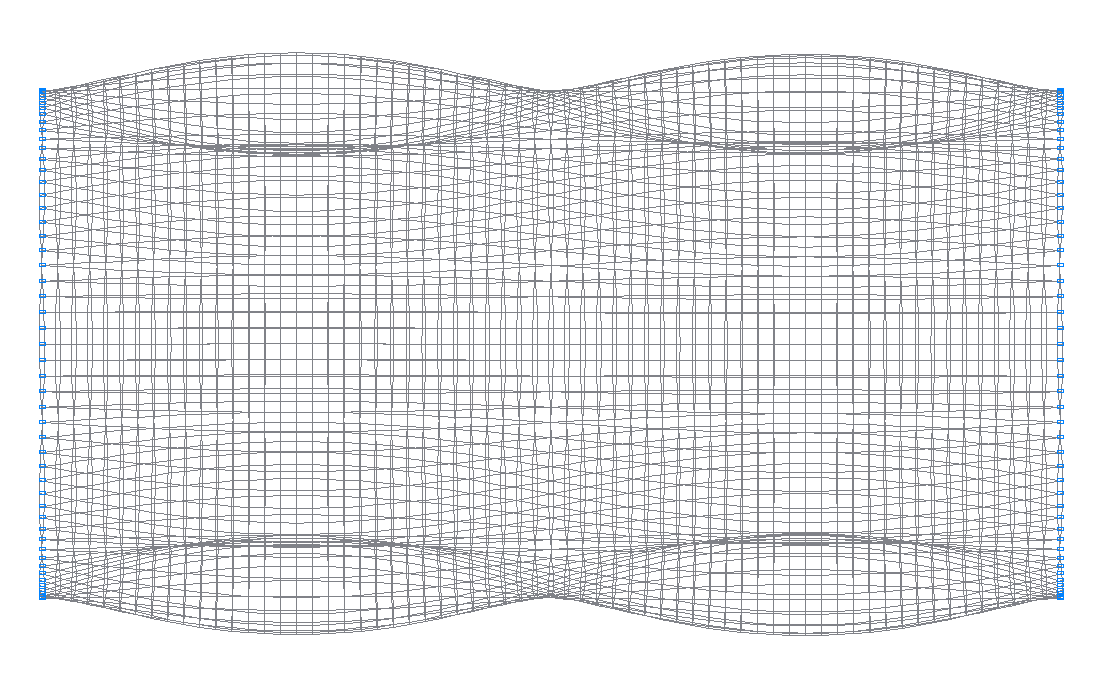
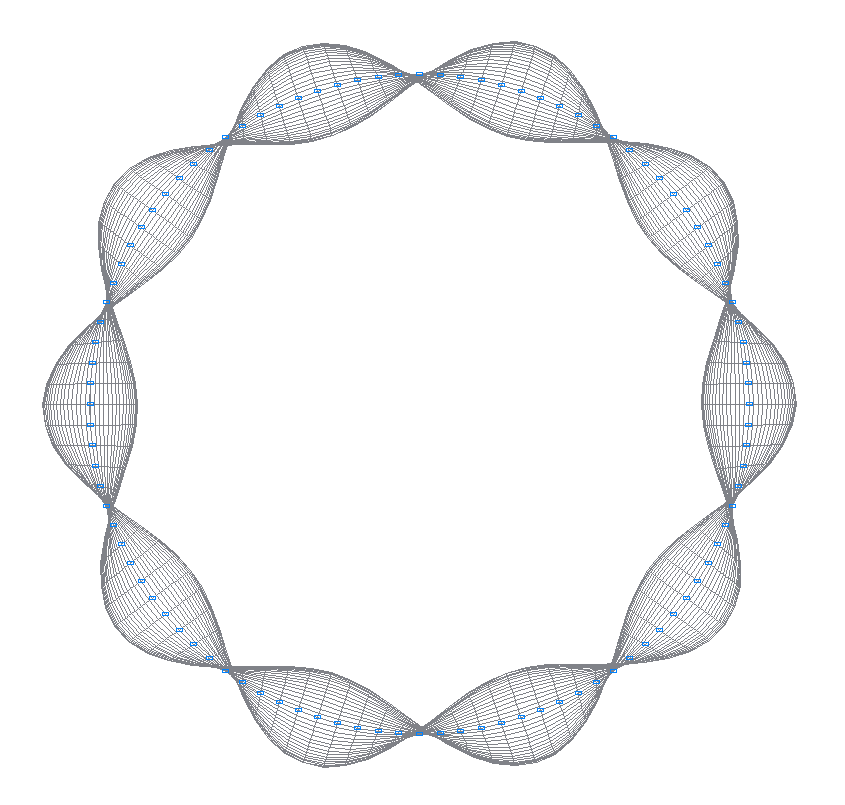
24-я (23-я теоретическая) собственная форма колебаний
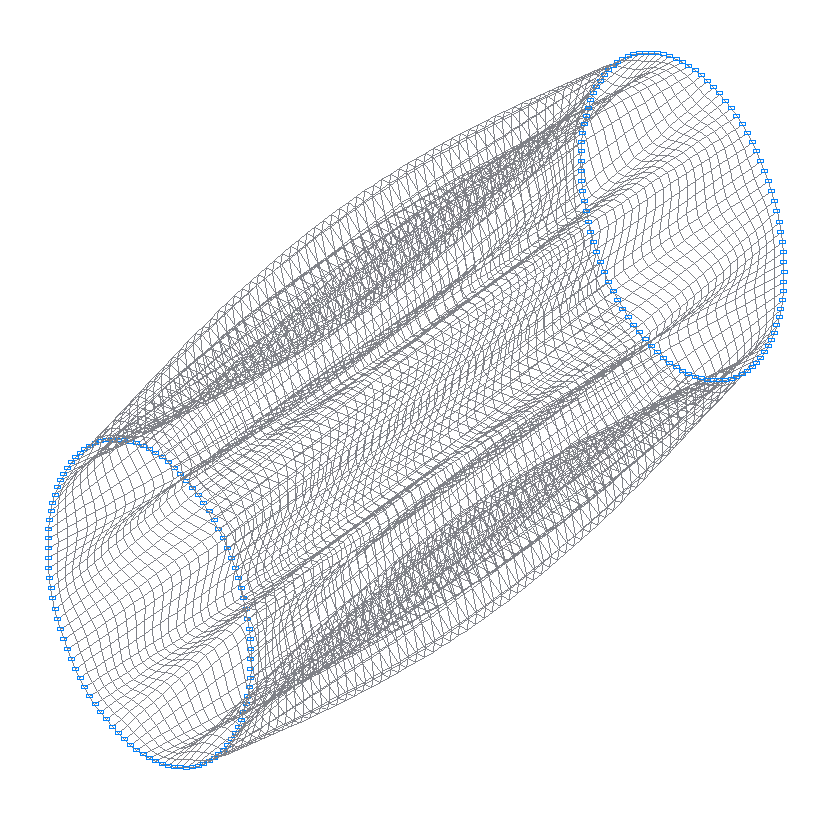

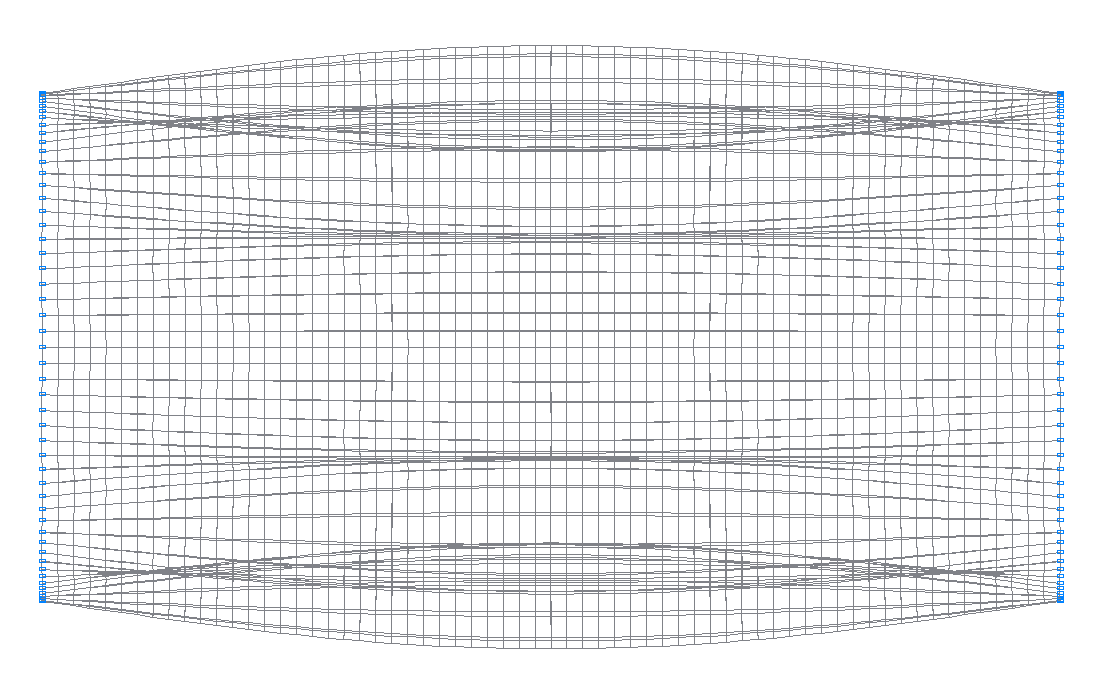
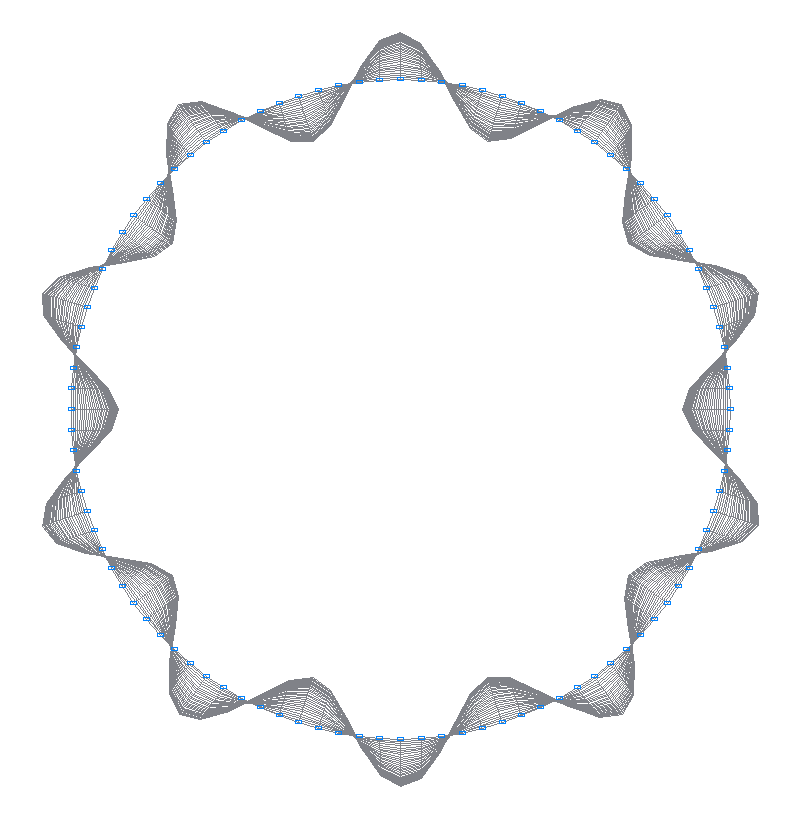
26-я (25-я теоретическая) собственная форма колебаний
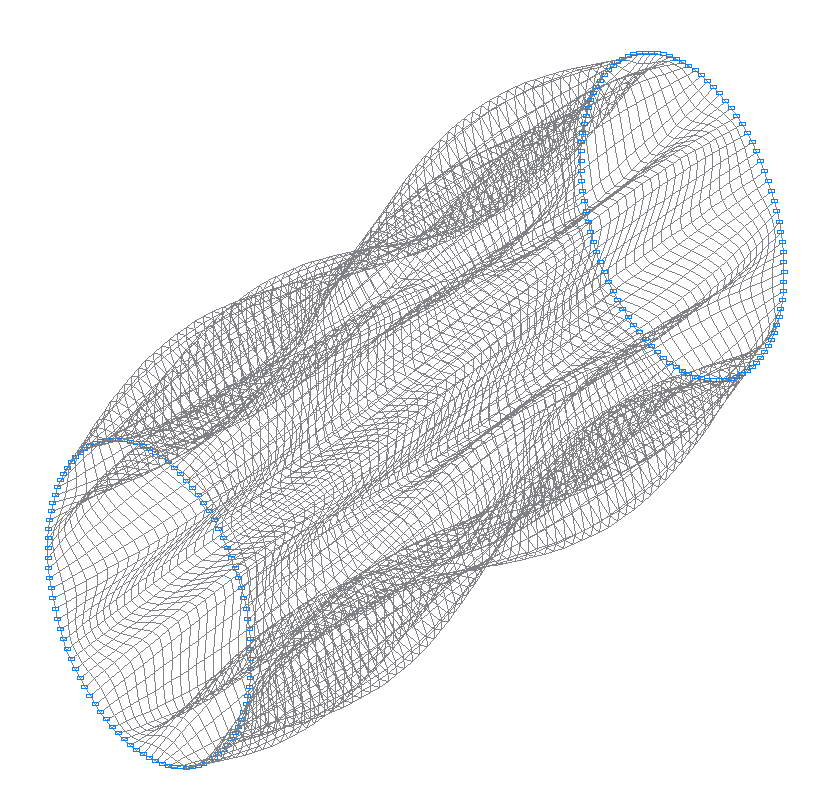
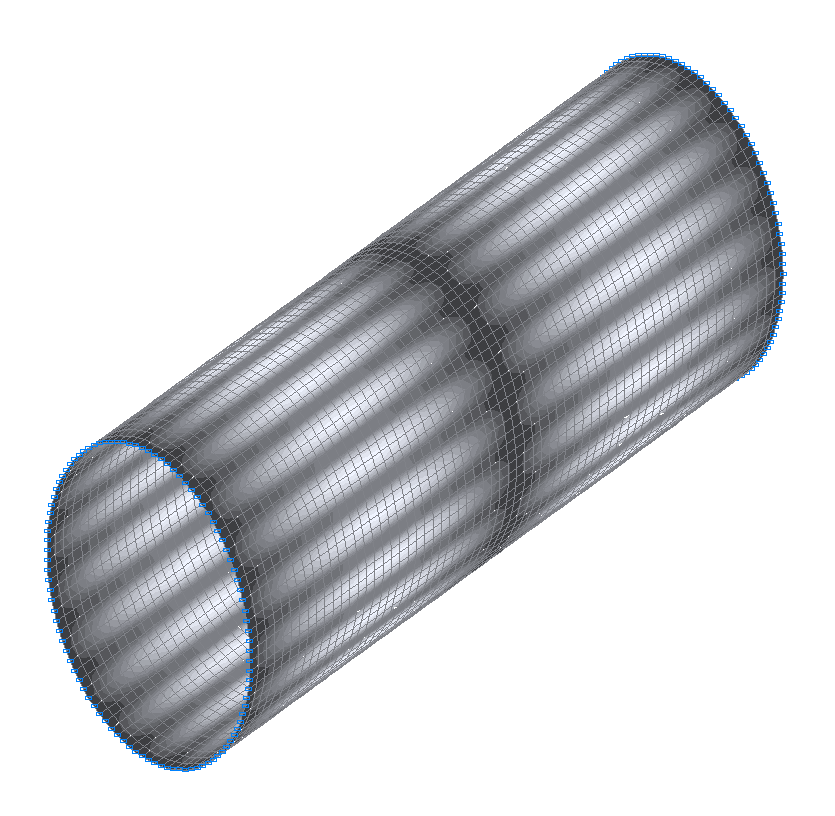
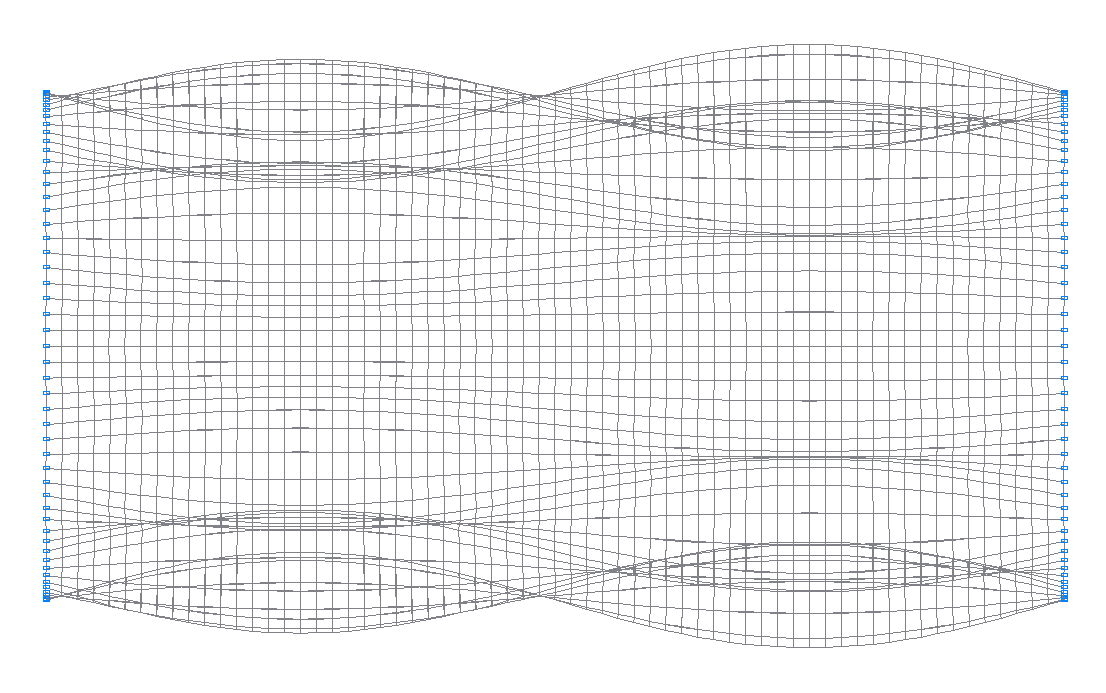
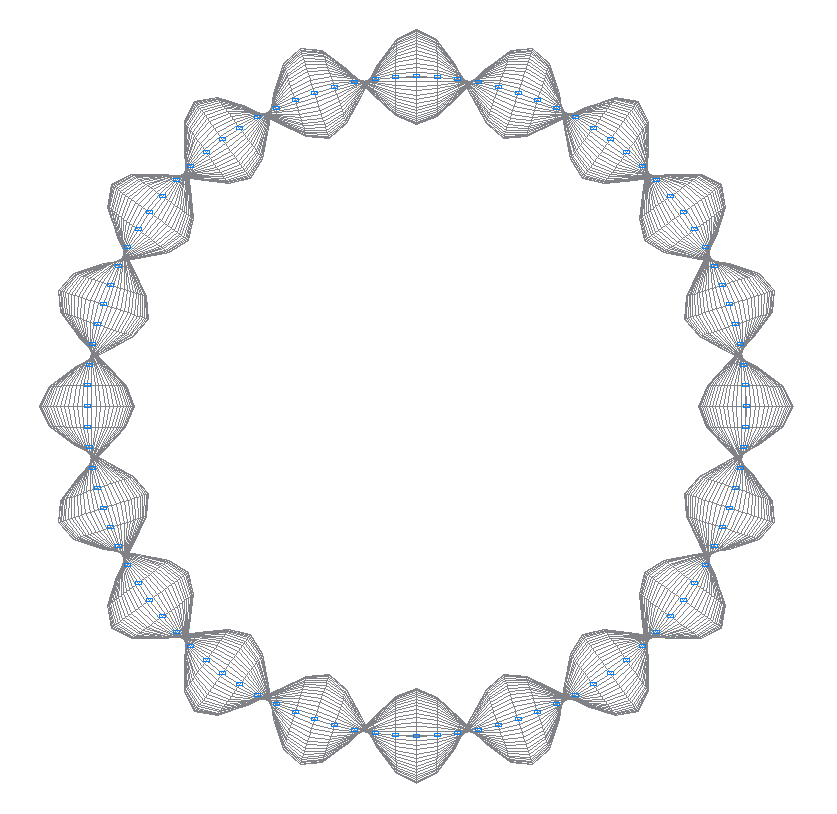
28-я (27-я теоретическая) собственная форма колебаний
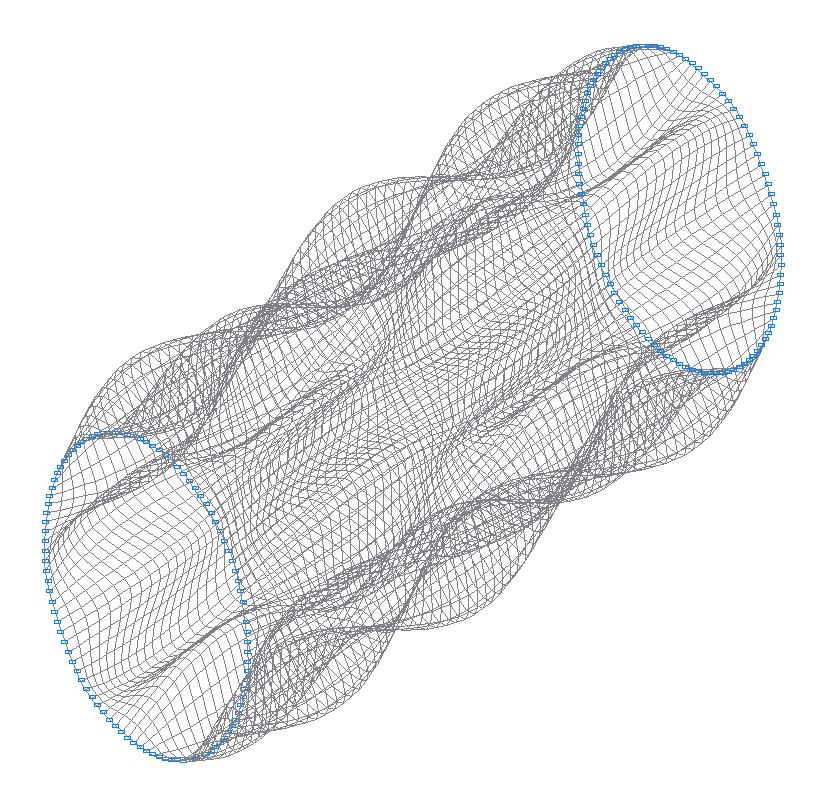
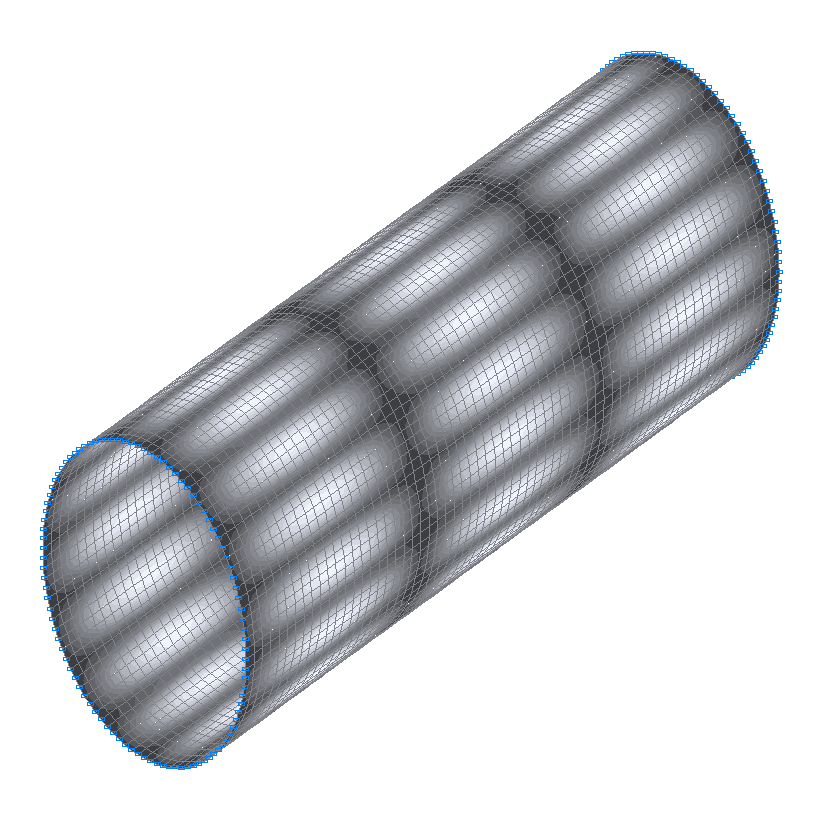
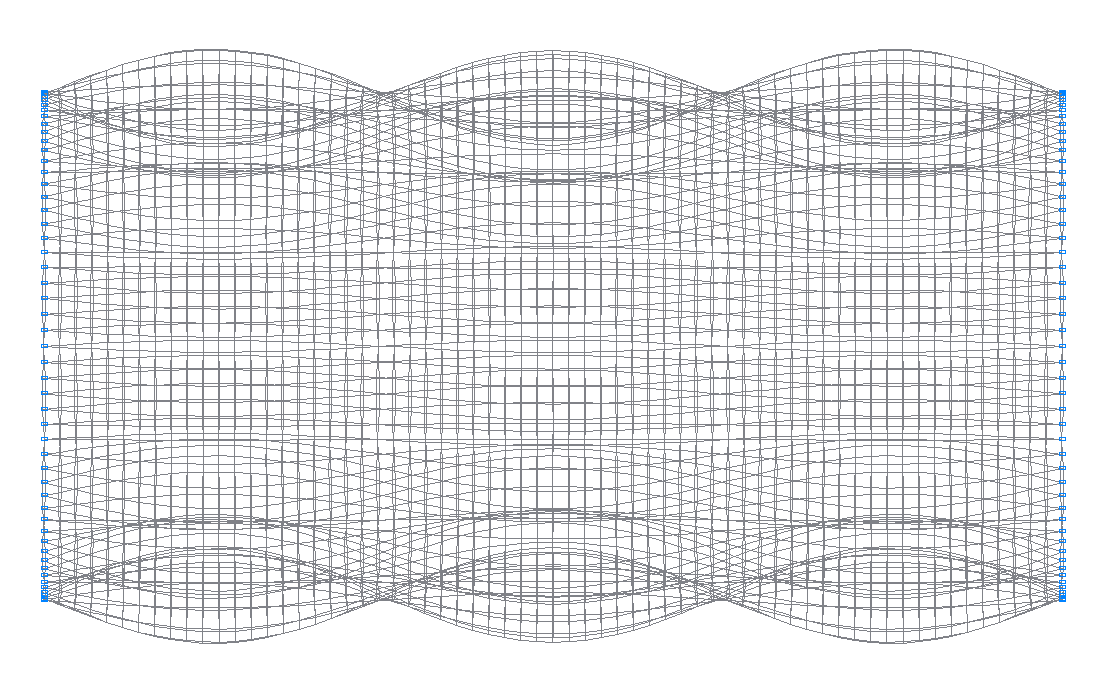
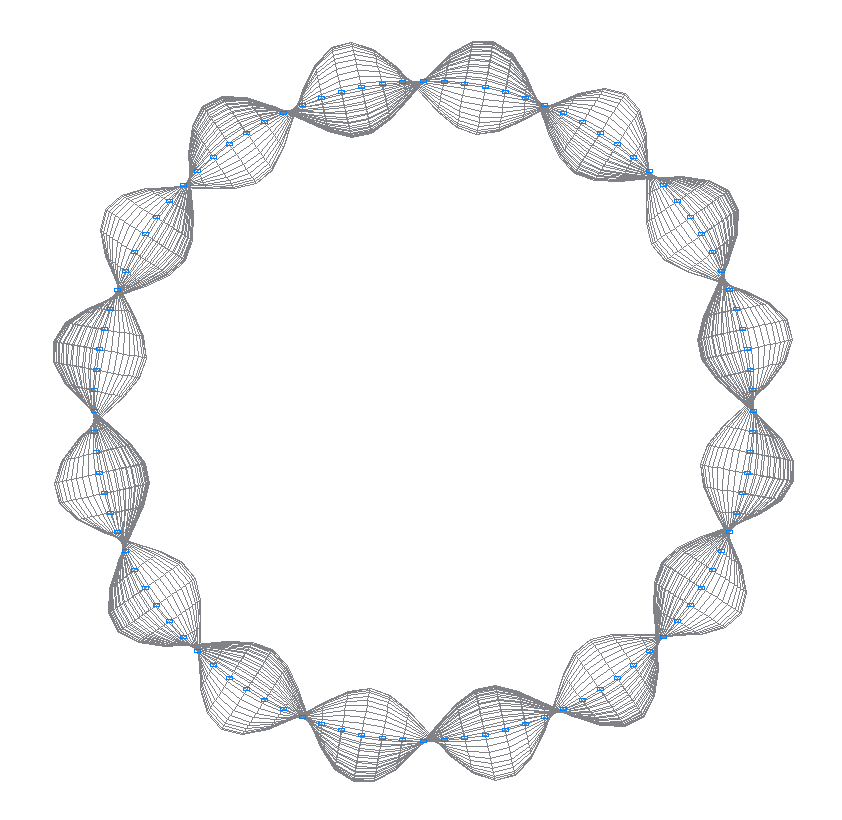
30-я (29-я теоретическая) собственная форма колебаний
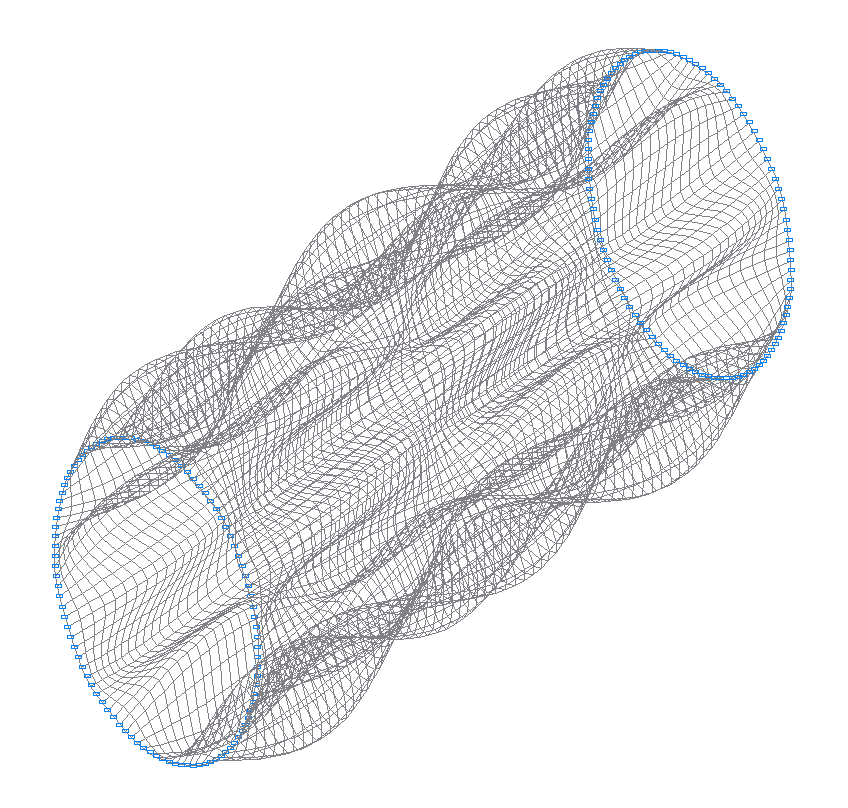
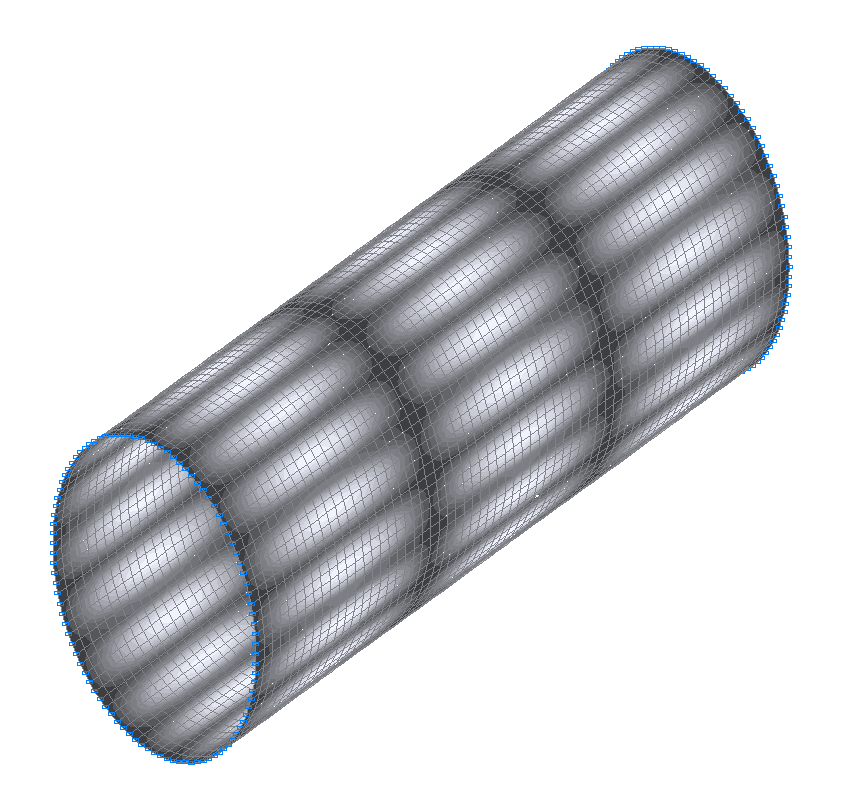
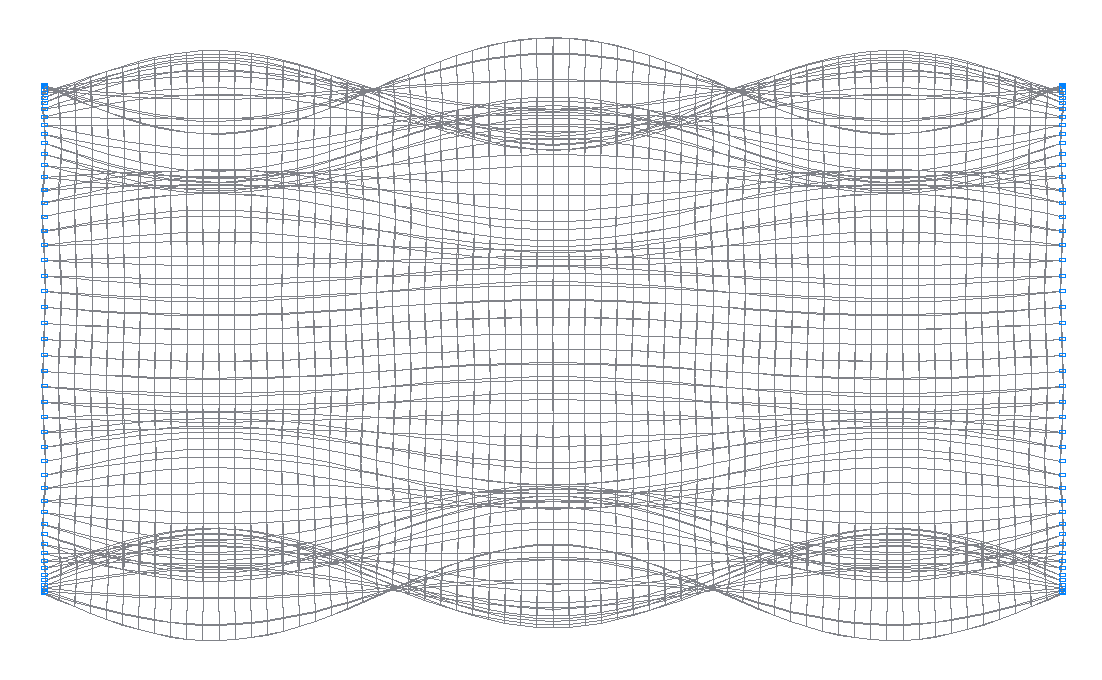
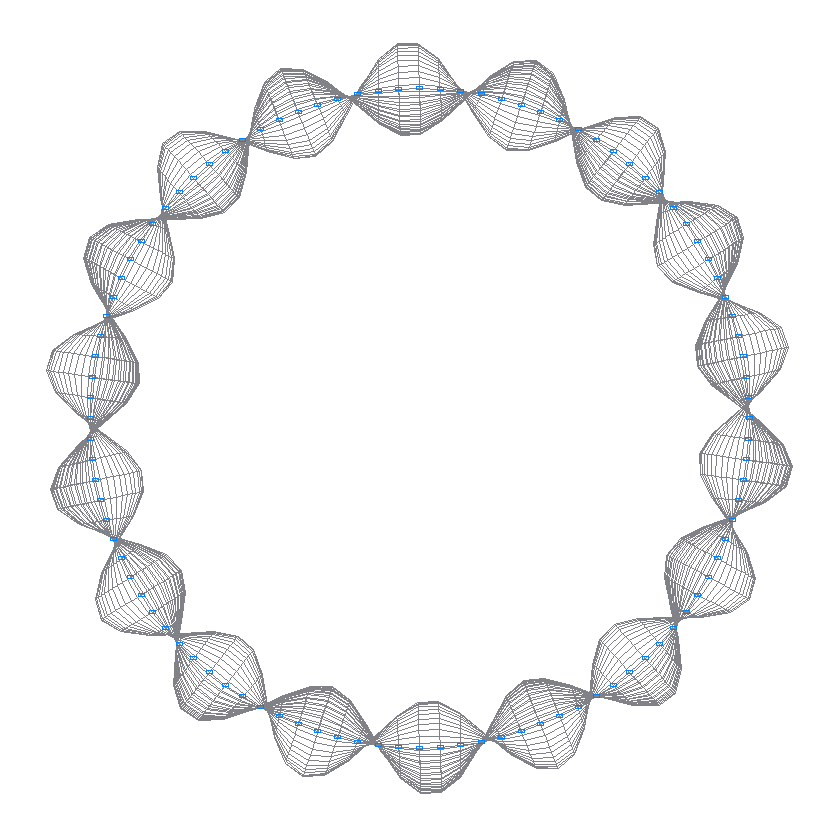
32-я (31-я теоретическая) собственная форма колебаний
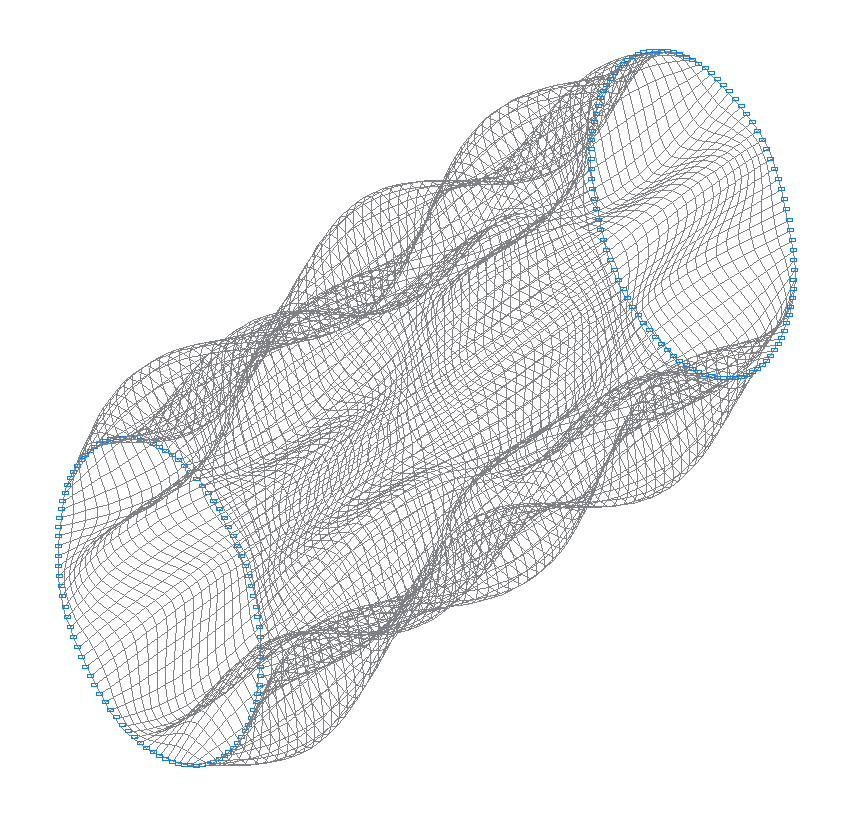
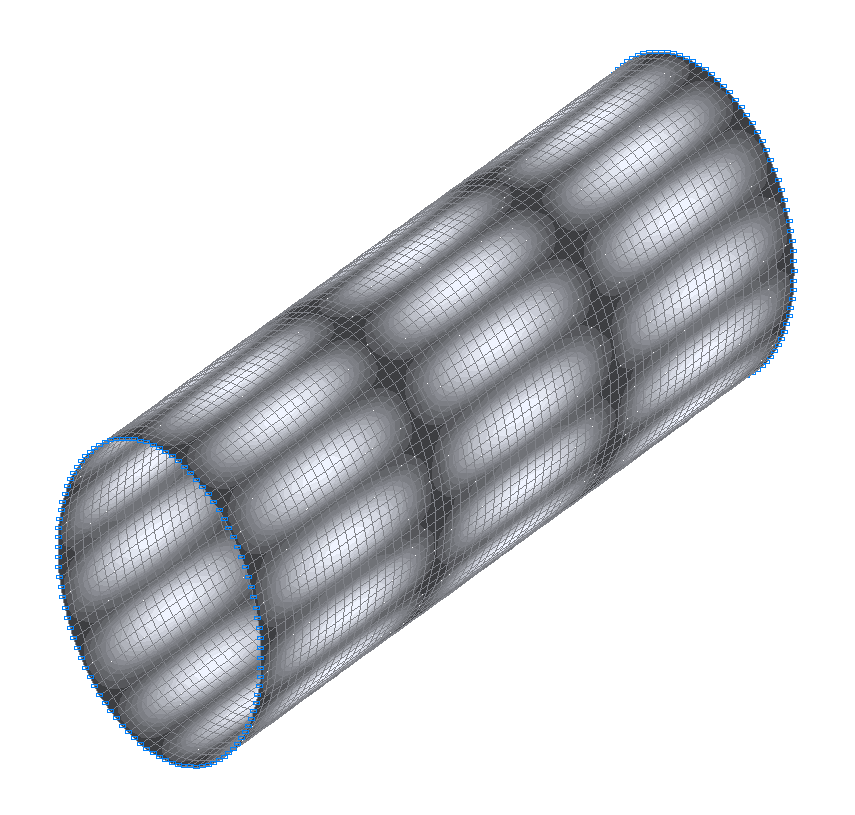
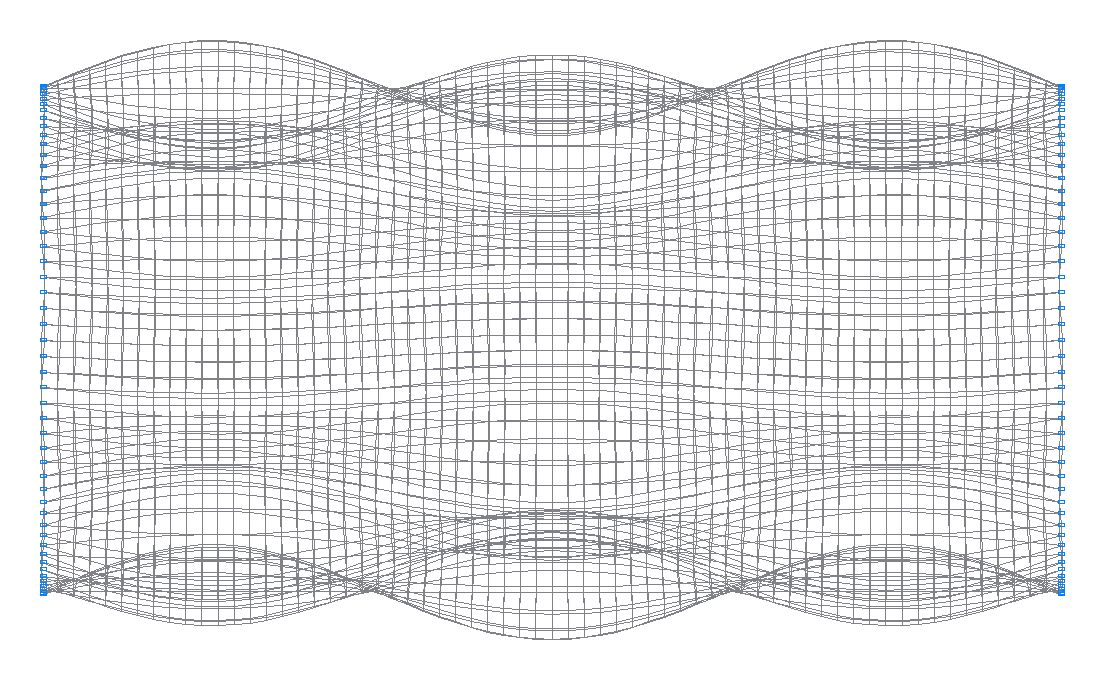
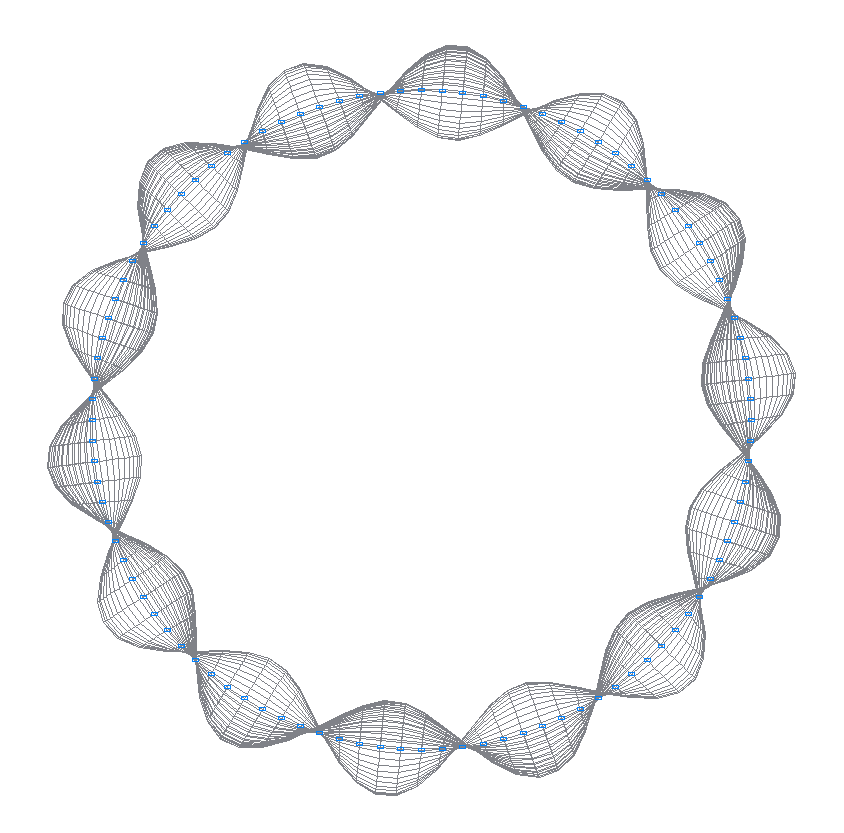
34-я (33-я теоретическая) собственная форма колебаний
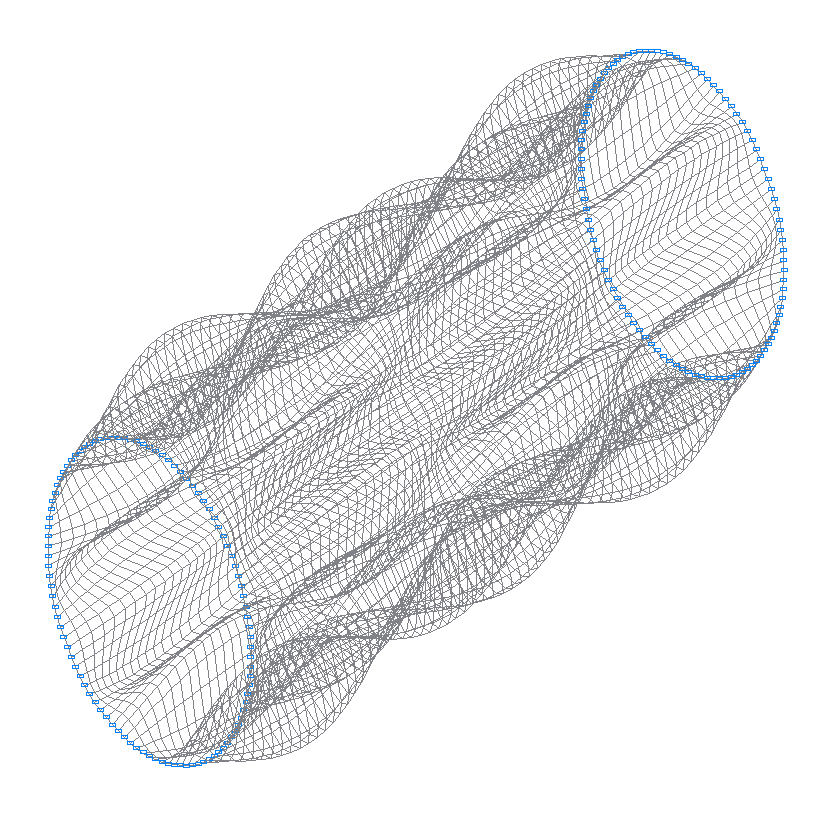
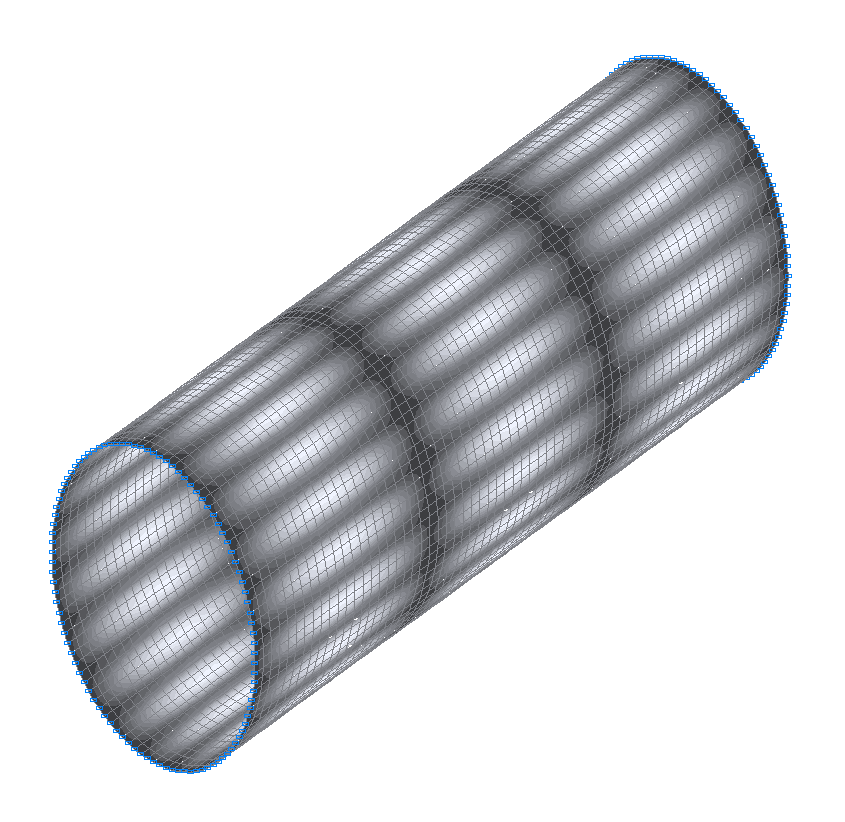
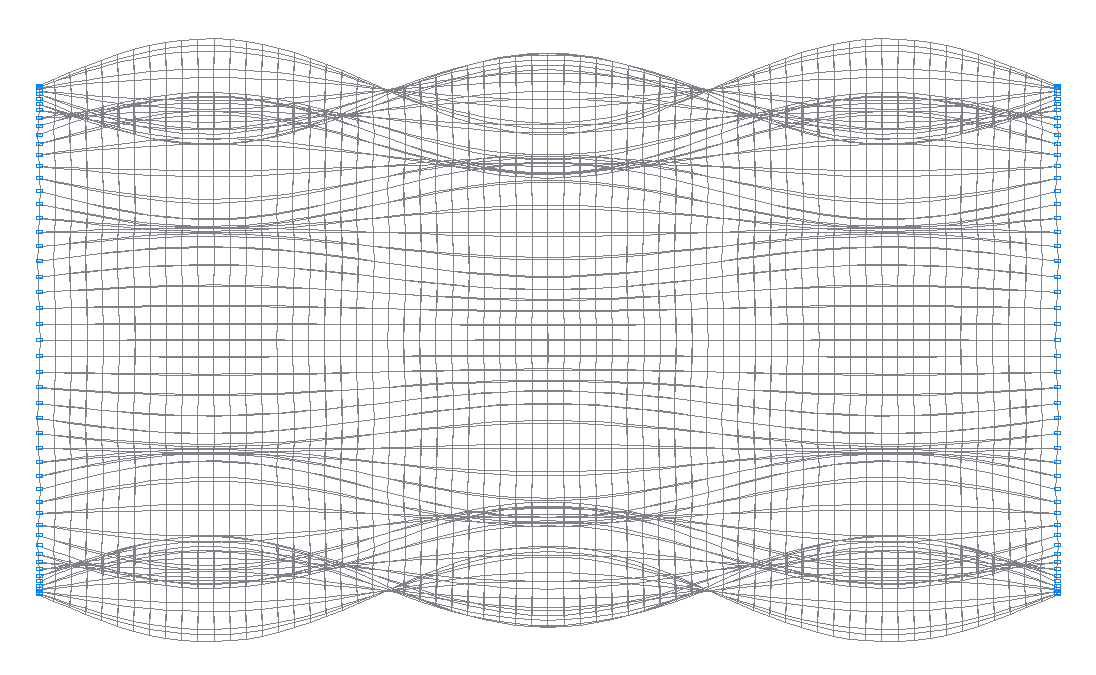
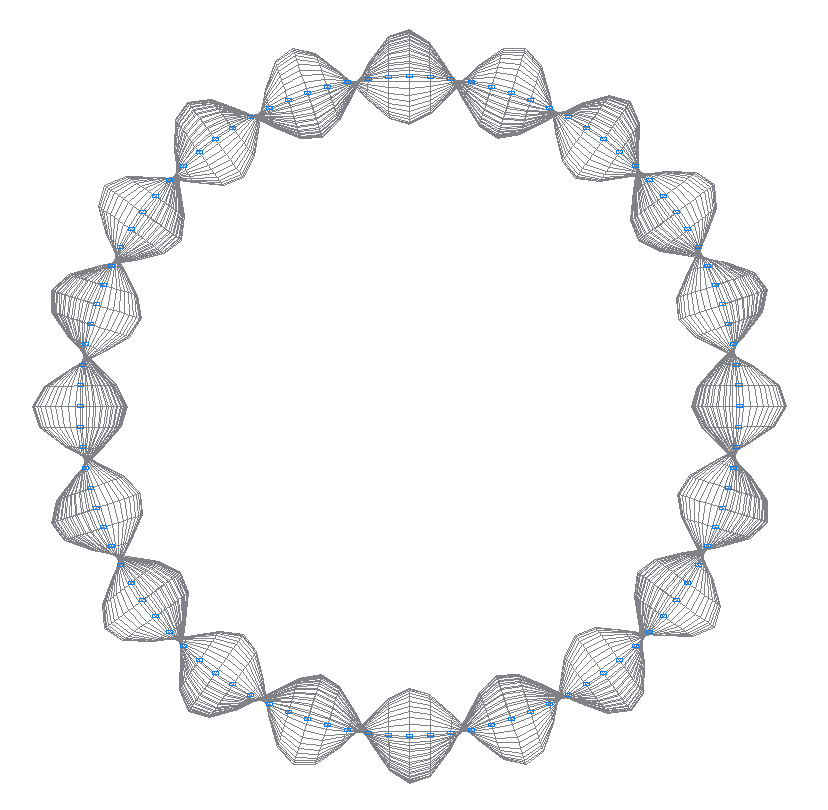
36-я (35-я теоретическая) собственная форма колебаний
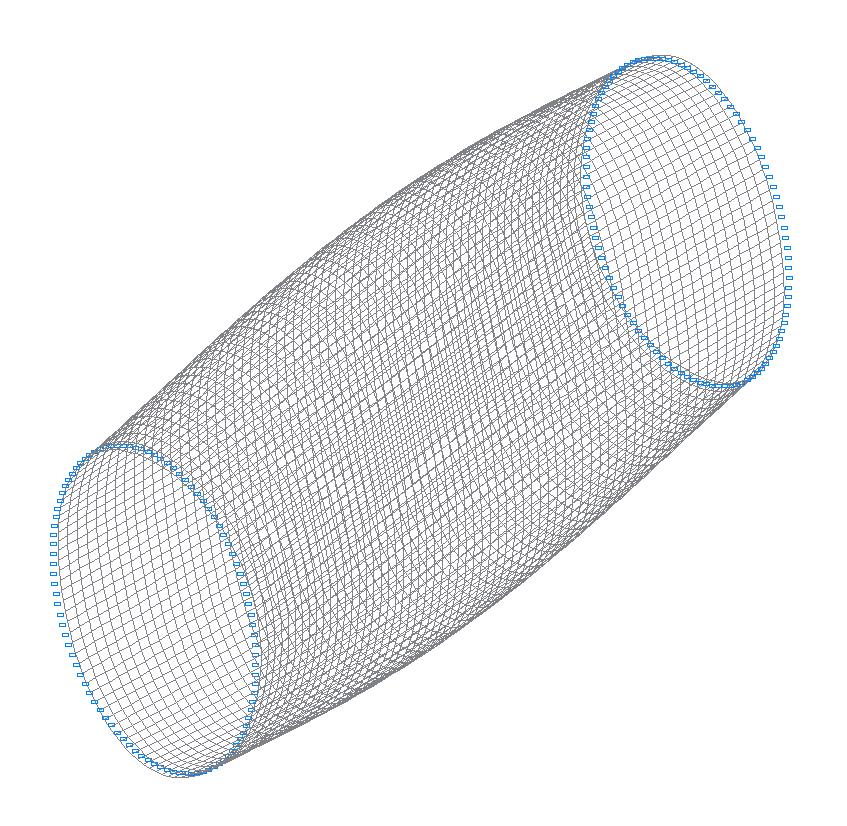


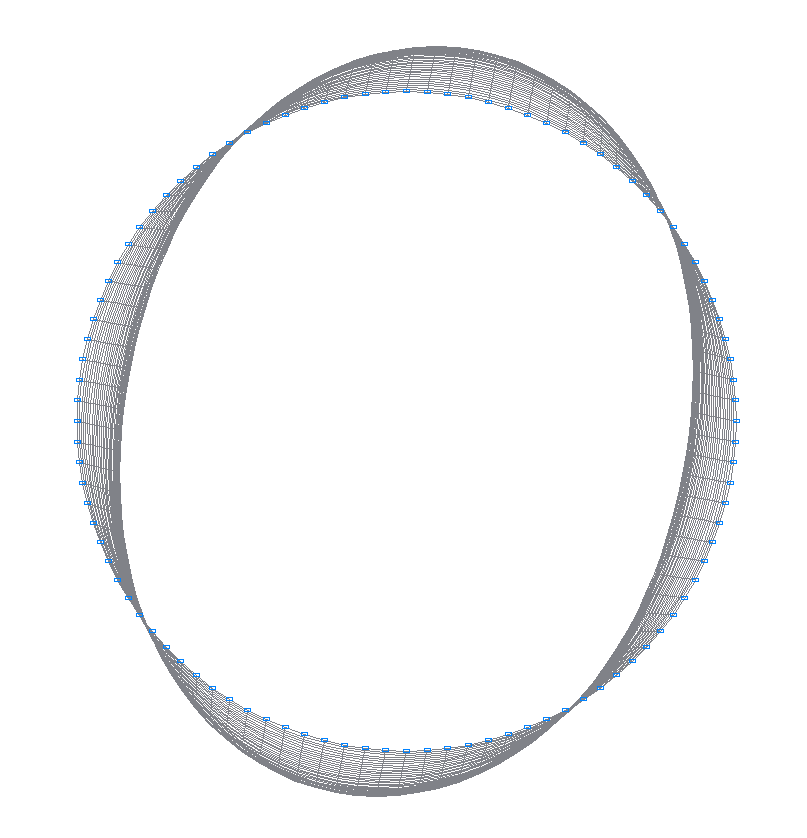
38-я (37-я теоретическая) собственная форма колебаний
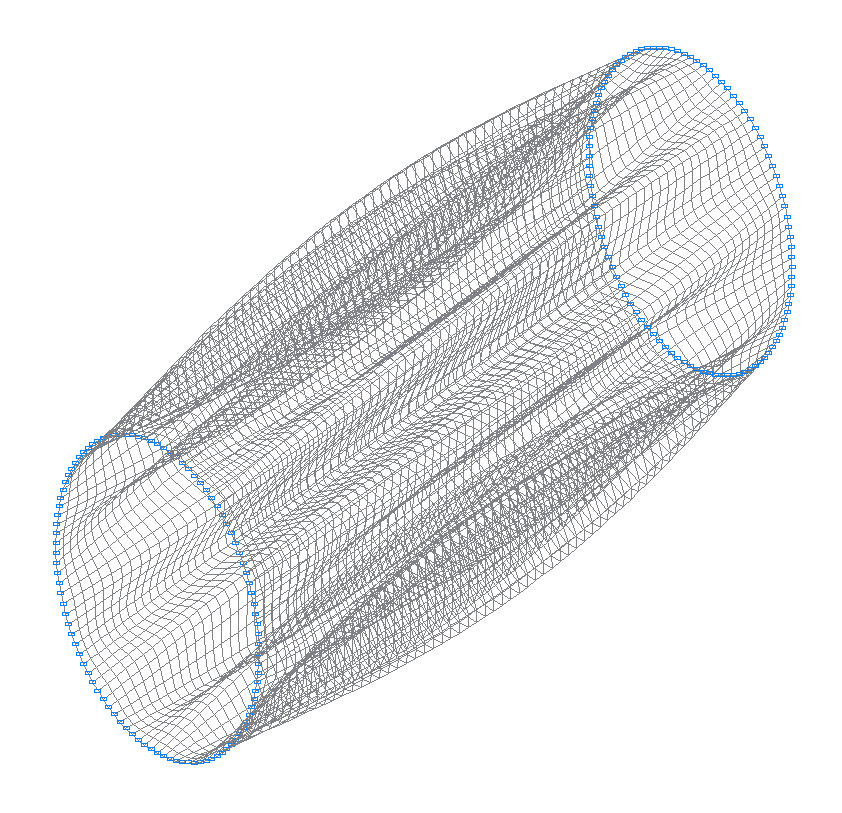

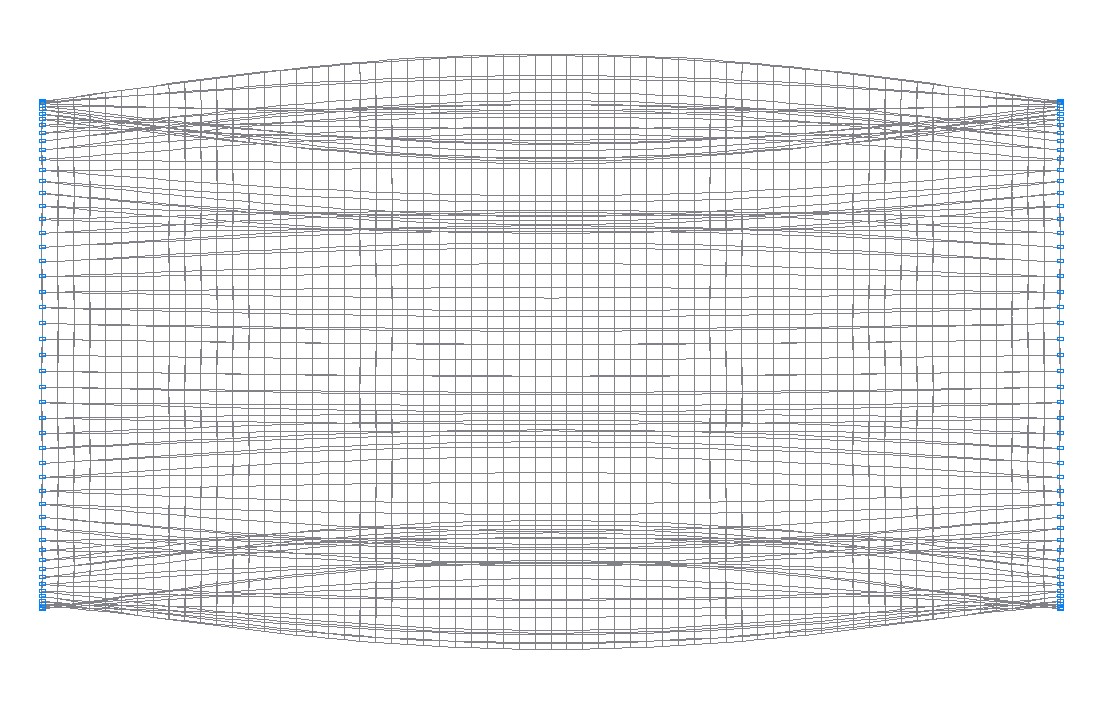
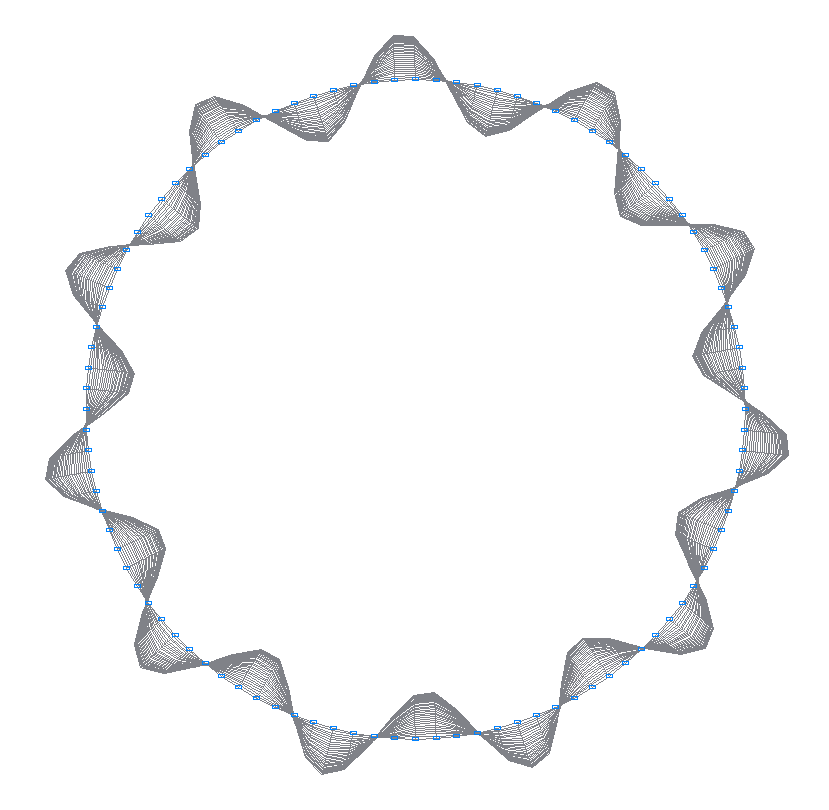
40-я (39-я теоретическая) собственная форма колебаний
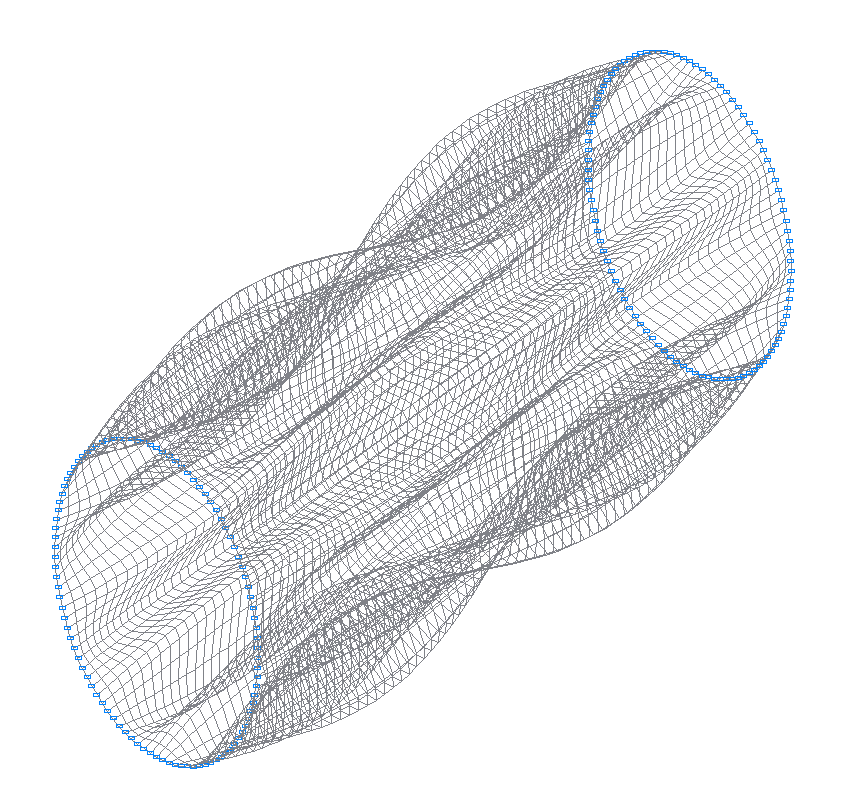
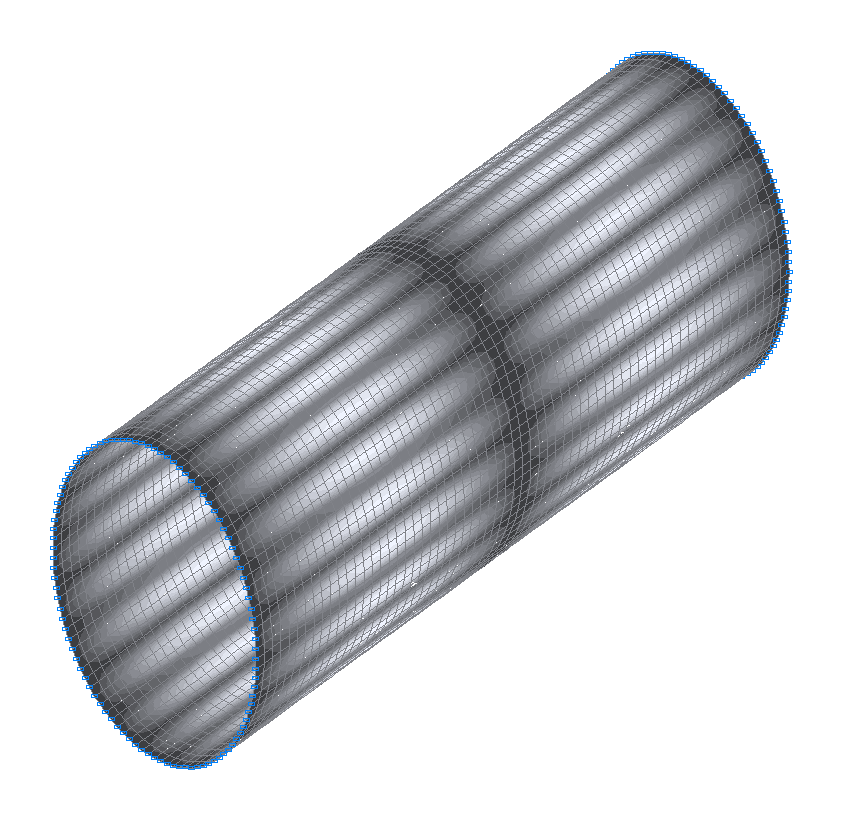

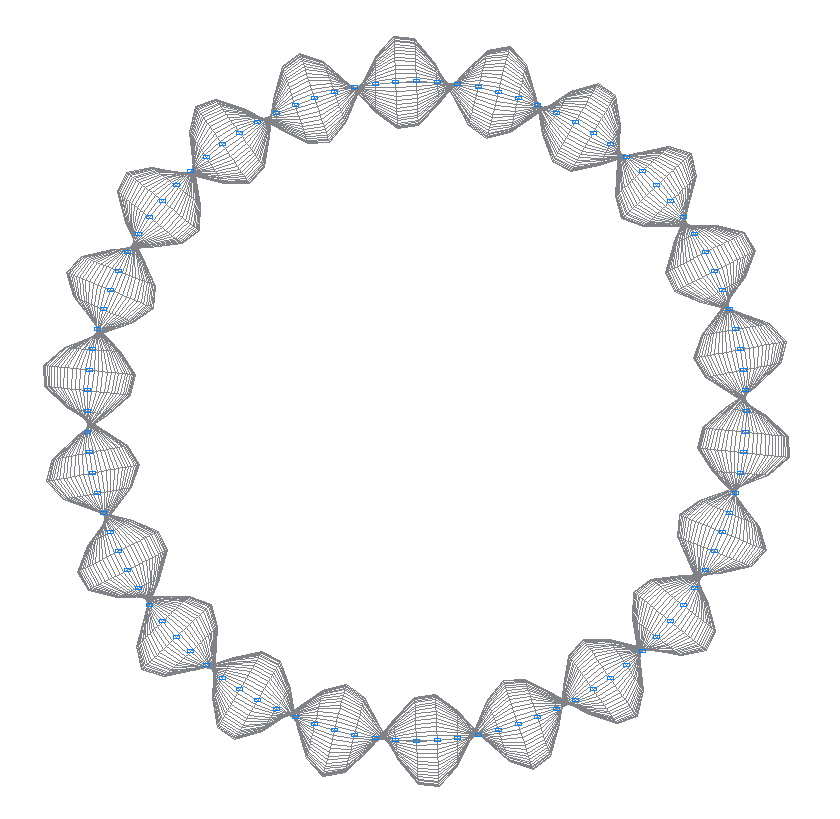
42-я (41-я теоретическая) собственная форма колебаний
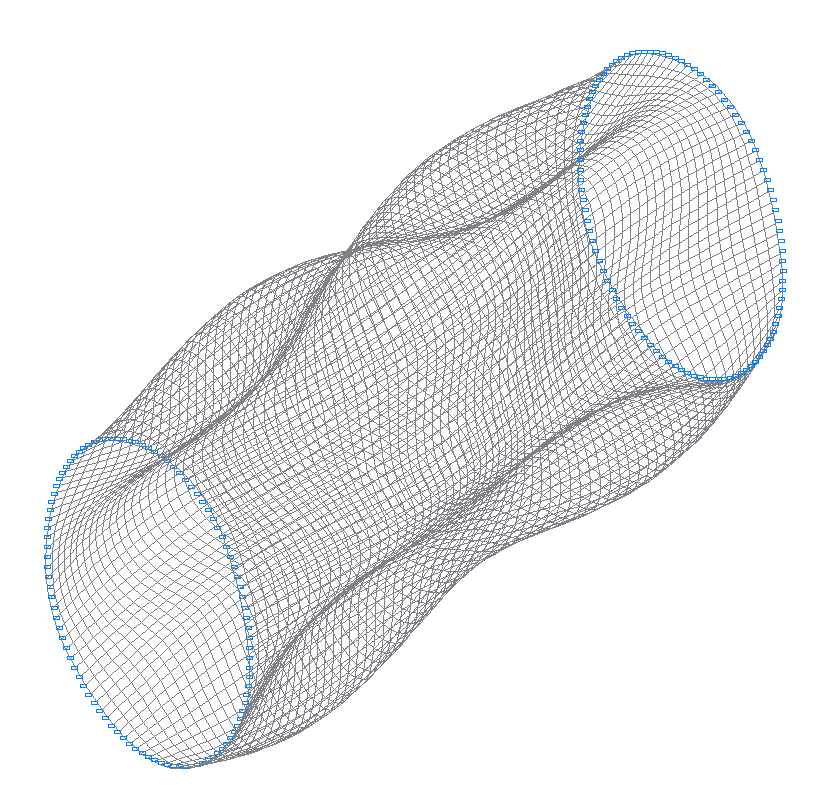

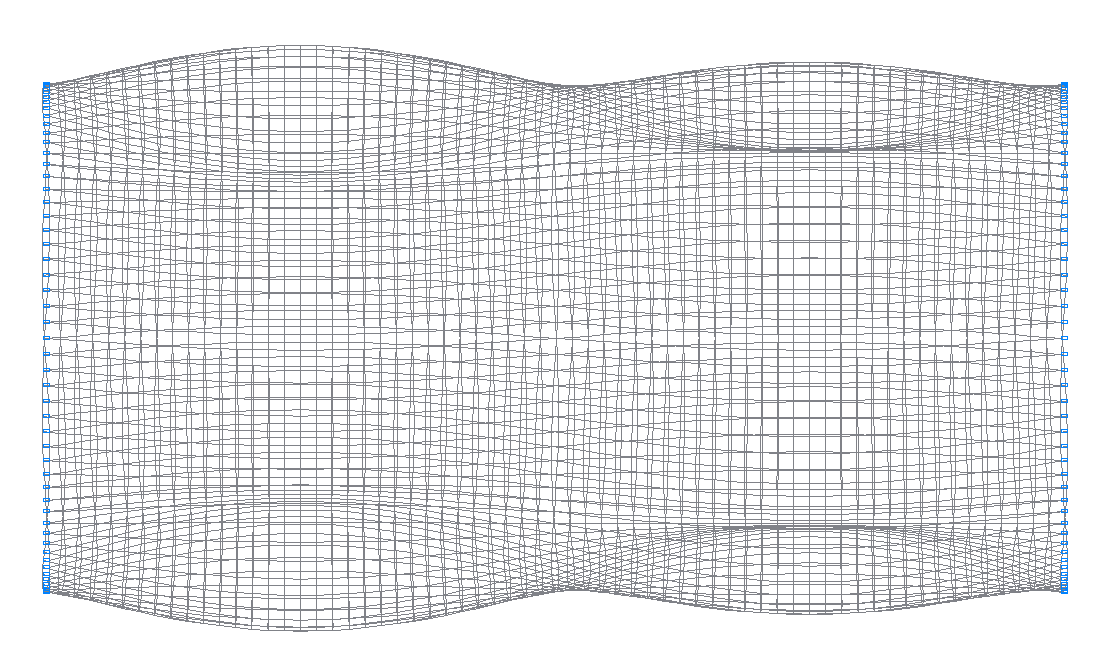
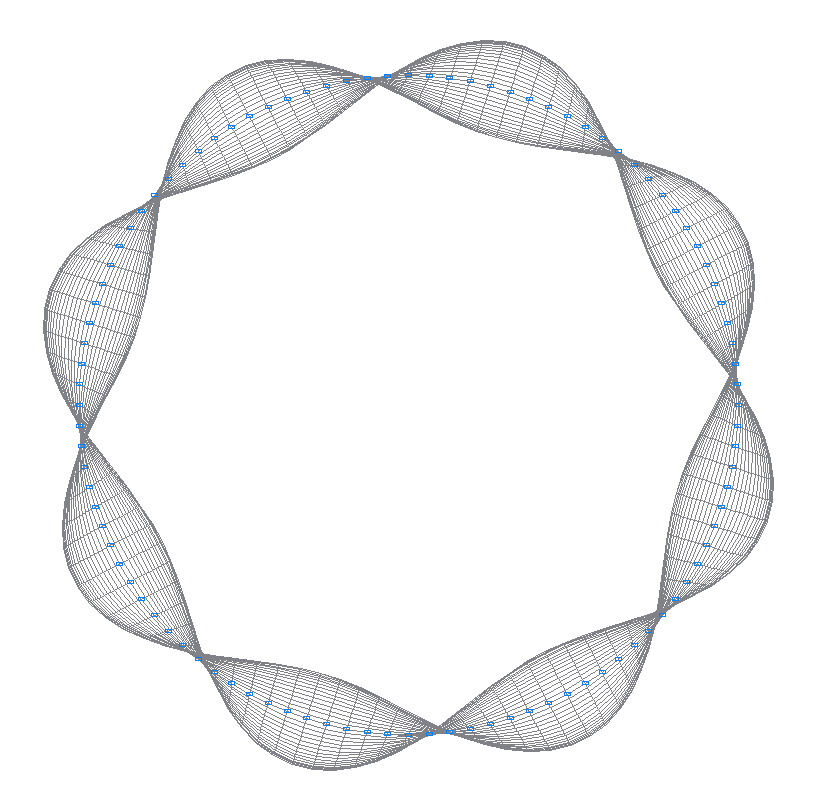
44-я (43-я теоретическая) собственная форма колебаний
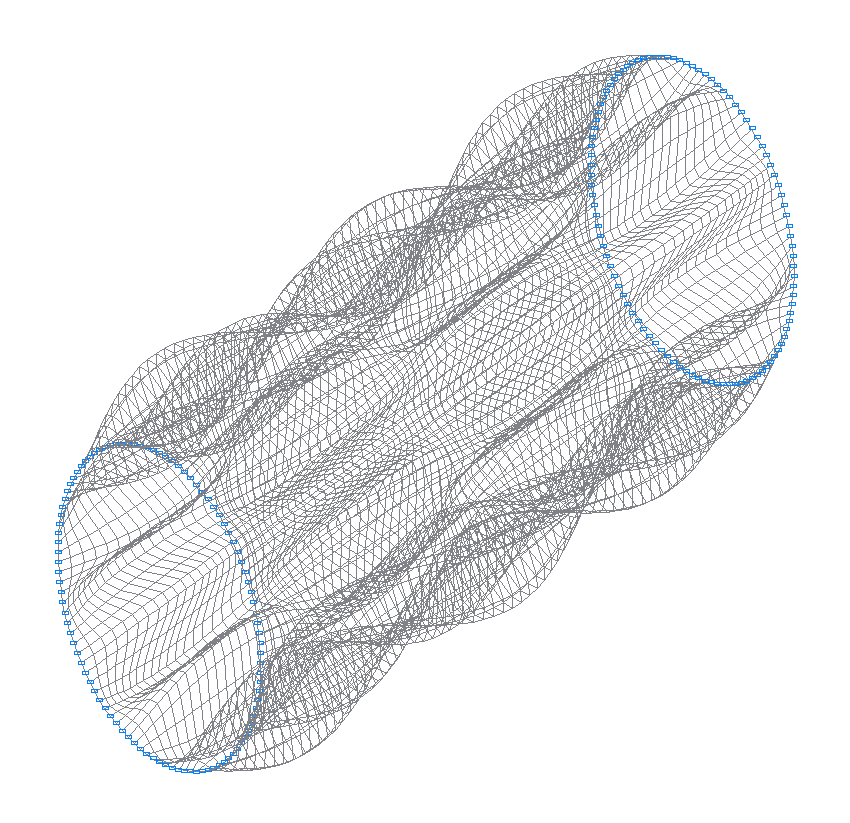
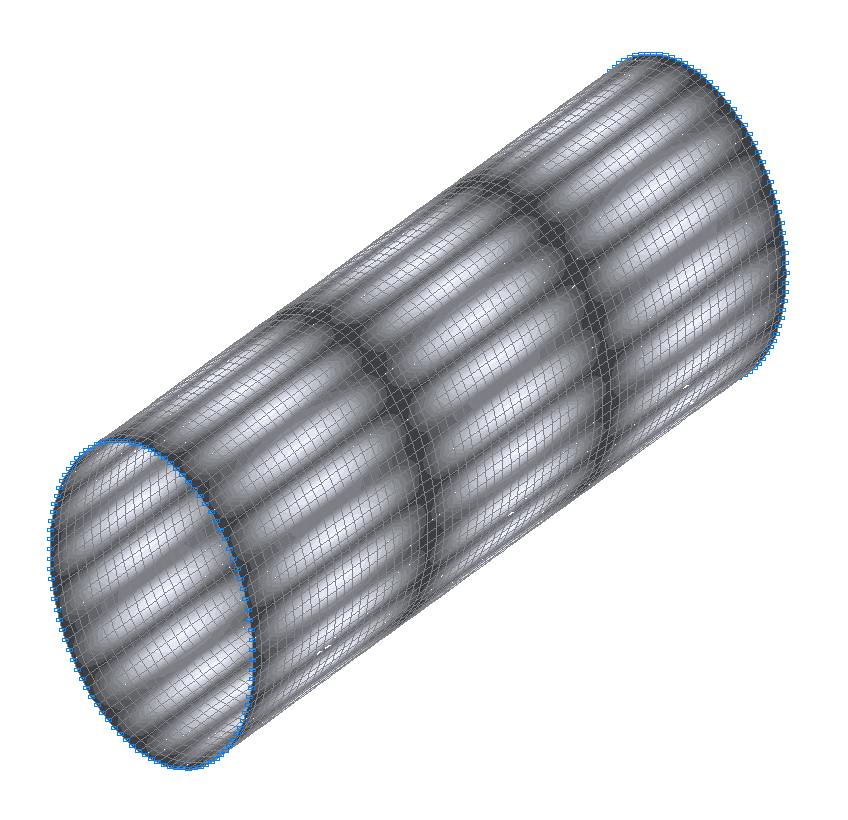
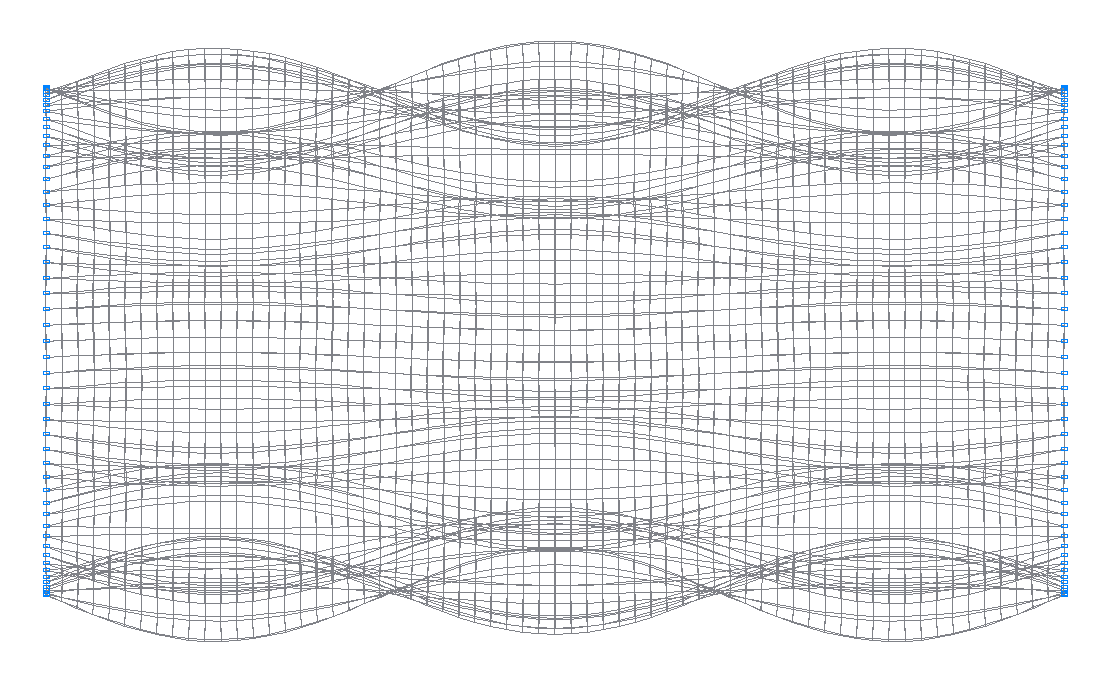
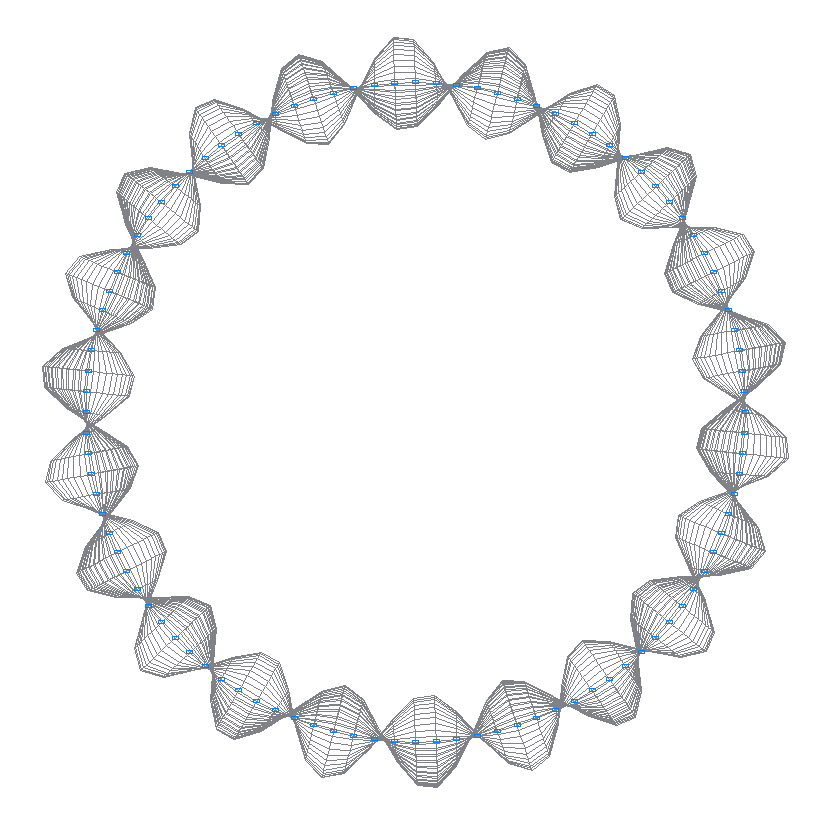
46-я (45-я теоретическая) собственная форма колебаний
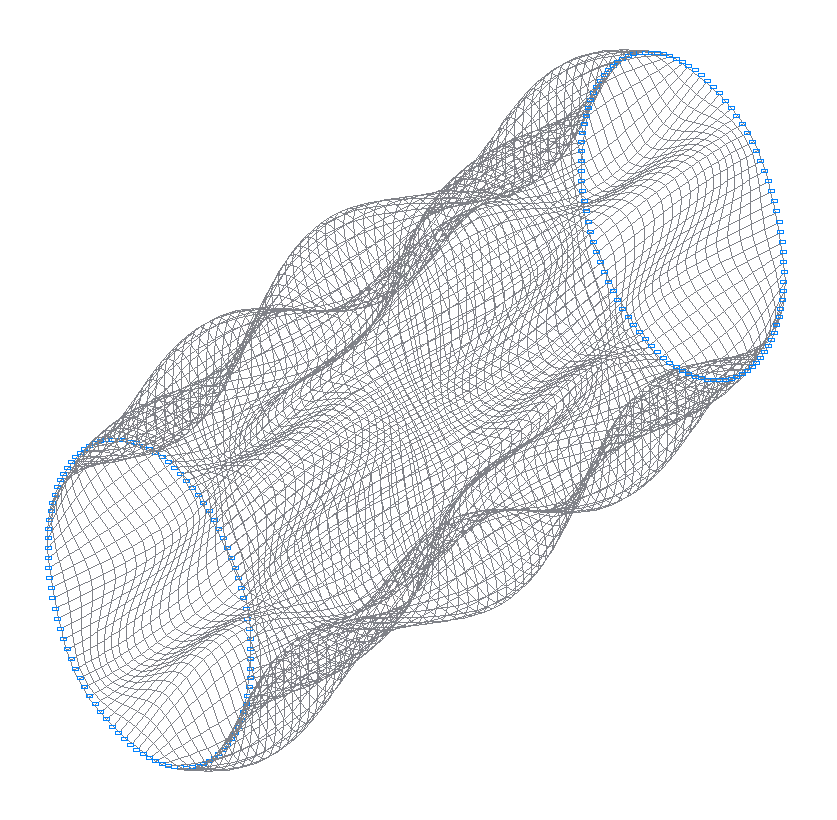
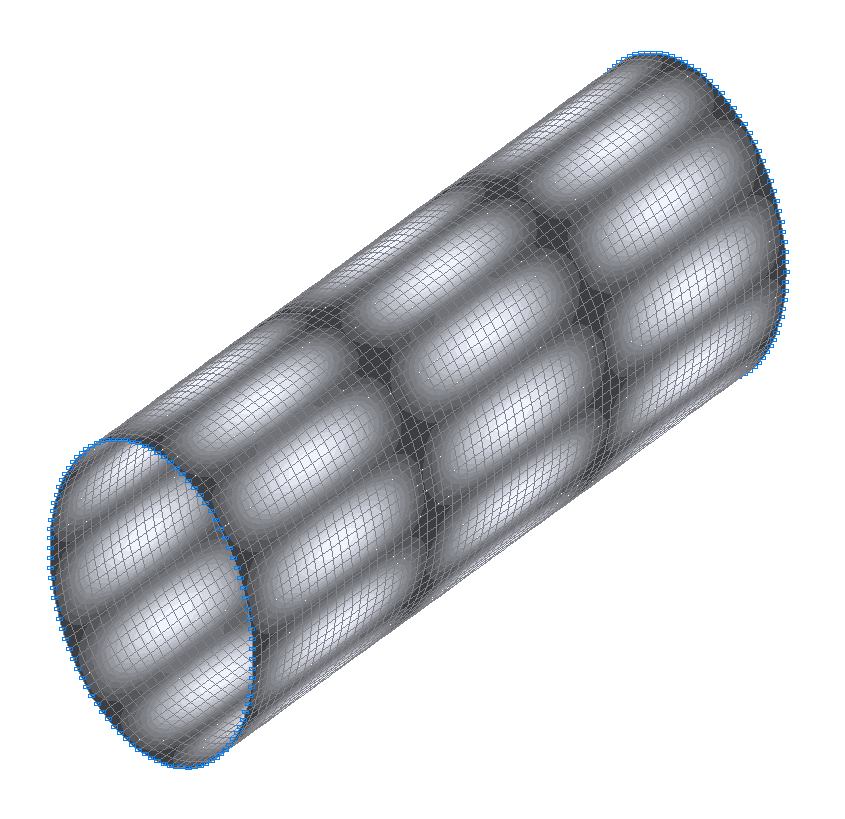
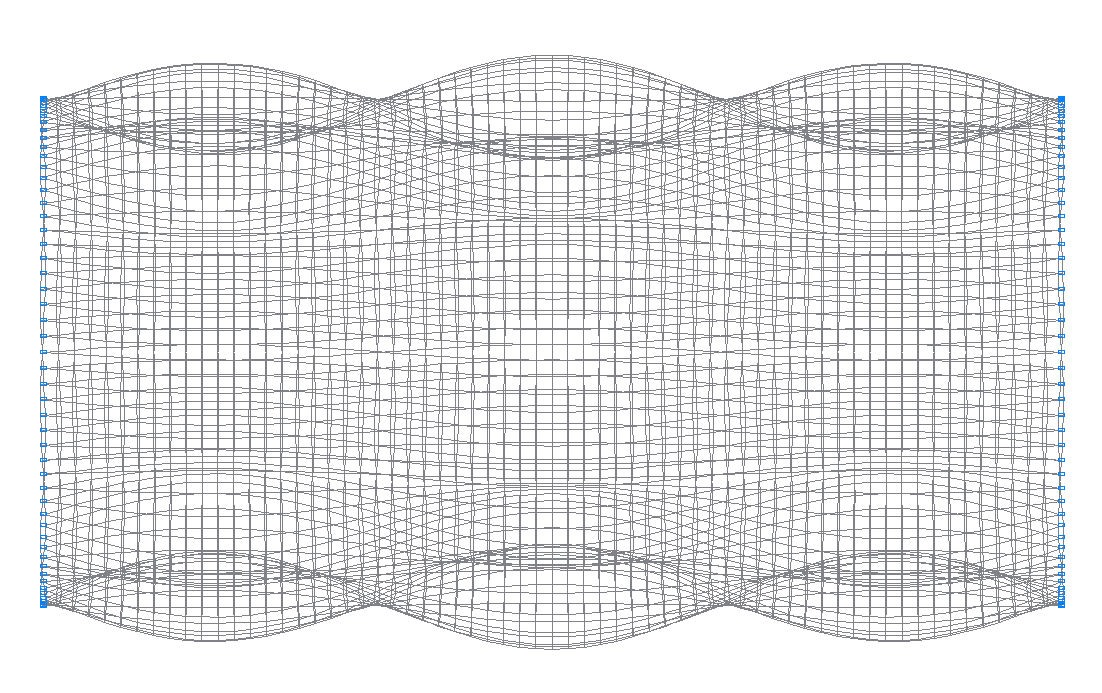
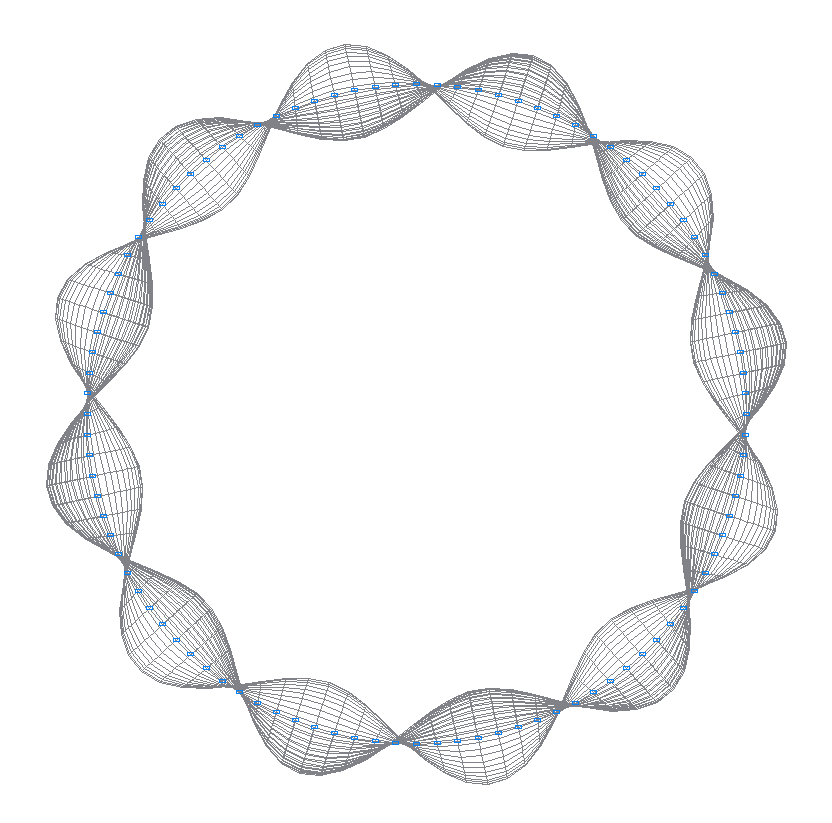
48-я (47-я теоретическая) собственная форма колебаний
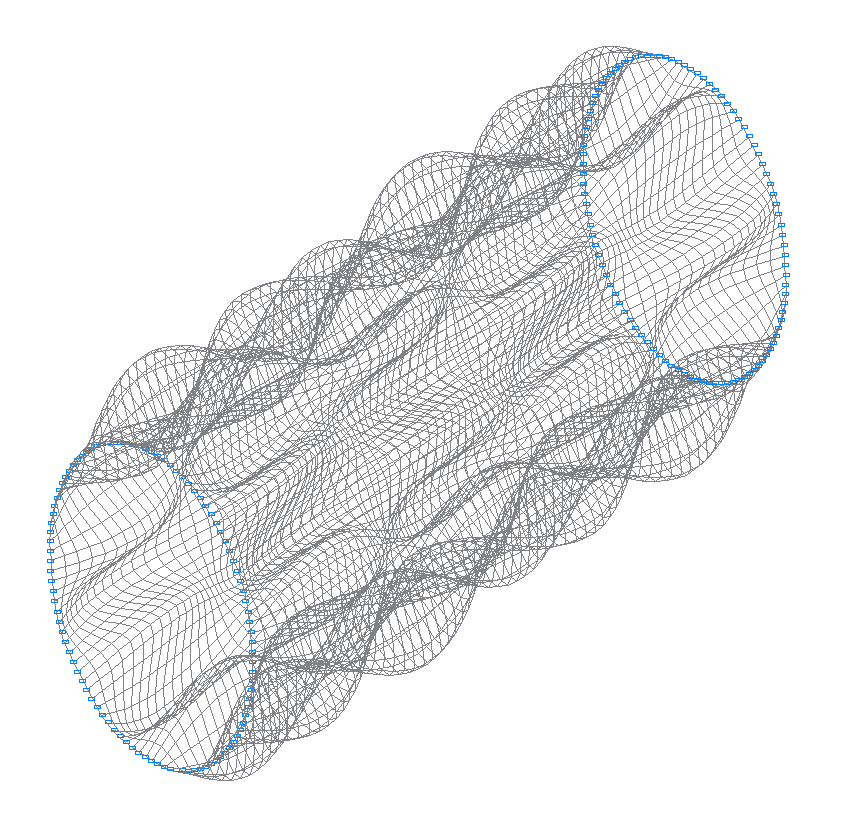
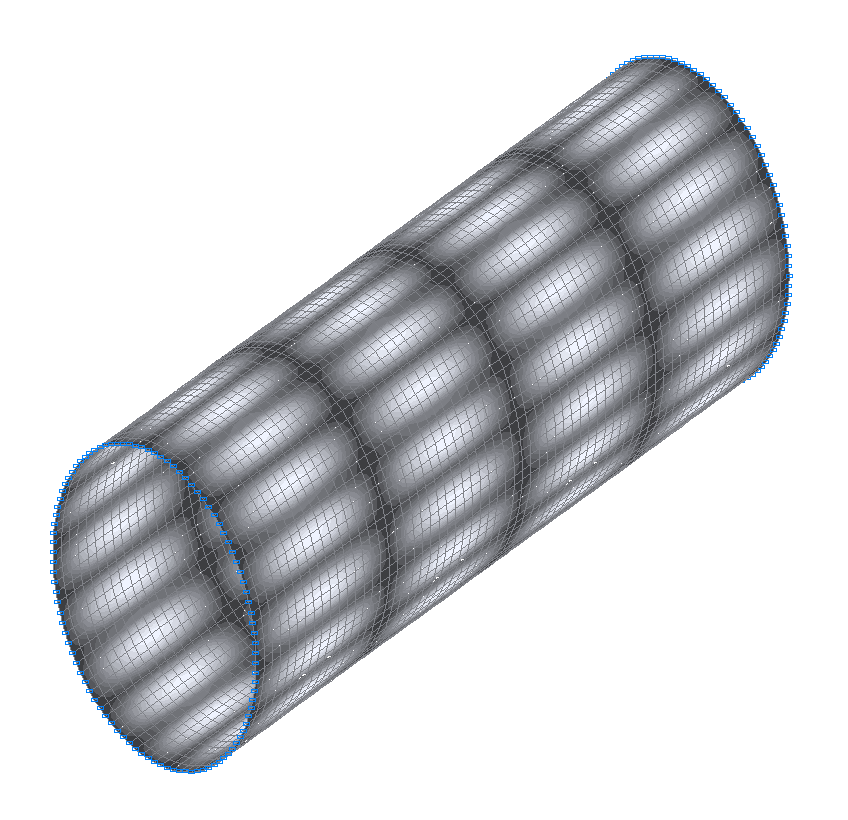
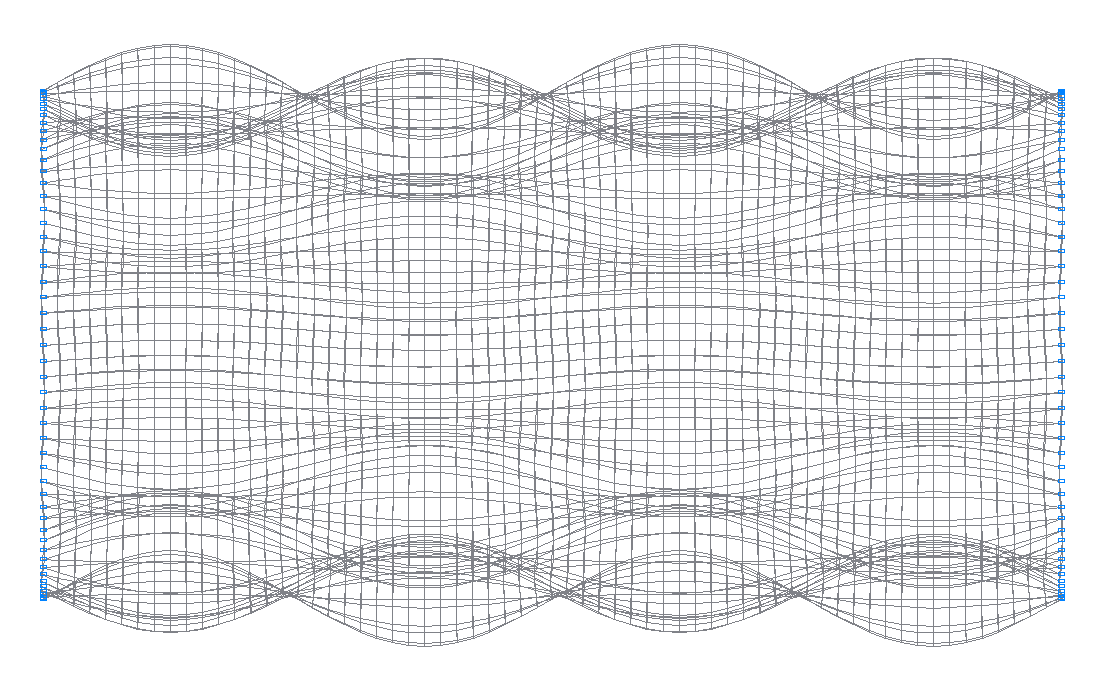
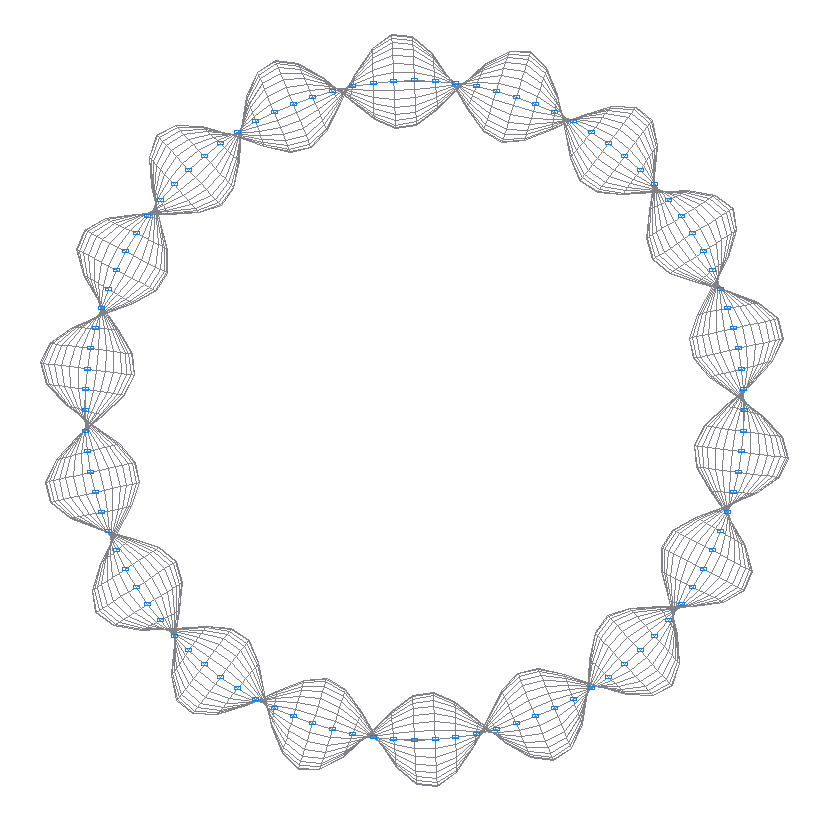
50-я (49-я теоретическая) собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, Гц
|
Форма колебаний |
Число узловых окружностей m и меридианов n |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1, 2 |
2, 5 |
354.4 |
354.9 |
0.14 |
|
3, 4 |
2, 6 |
408.3 |
408.9 |
0.15 |
|
5, 6 |
2, 4 |
409.5 |
410.1 |
0.15 |
|
7, 8 |
2, 7 |
522.1 |
522.9 |
0.15 |
|
9, 10 |
2, 3 |
642.1 |
642.8 |
0.11 |
|
11, 12 |
2, 8 |
671.1 |
672.0 |
0.13 |
|
13, 14 |
3, 7 |
723.2 |
724.9 |
0.24 |
|
15, 16 |
3, 6 |
768.5 |
770.3 |
0.23 |
|
17, 18 |
3, 8 |
784.3 |
785.9 |
0.20 |
|
19, 20 |
2, 9 |
846.2 |
847.3 |
0.13 |
|
21, 22 |
3, 9 |
914.9 |
916.6 |
0.19 |
|
23, 24 |
3, 5 |
962.3 |
964.5 |
0.23 |
|
25, 26 |
2, 10 |
1044.3 |
1045.7 |
0.13 |
|
27, 28 |
3, 10 |
1090.7 |
1092.5 |
0.17 |
|
29, 30 |
4, 8 |
1095.6 |
1099.3 |
0.34 |
|
31, 32 |
4, 9 |
1115.7 |
1119.2 |
0.31 |
|
33, 34 |
4, 7 |
1194.2 |
1198.2 |
0.33 |
|
35, 36 |
4, 10 |
1223.2 |
1226.5 |
0.27 |
|
37, 38 |
2, 2 |
1241.3 |
1242.5 |
0.10 |
|
39, 40 |
2, 11 |
1264.3 |
1265.9 |
0.13 |
|
41, 42 |
3, 11 |
1299.1 |
1301.2 |
0.16 |
|
43, 44 |
3, 4 |
1368.6 |
1370.9 |
0.17 |
|
45, 46 |
4, 11 |
1391.6 |
1395.0 |
0.24 |
|
47, 48 |
4, 6 |
1444.4 |
1448.8 |
0.30 |
|
49, 50 |
5, 9 |
1470.4 |
1477.2 |
0.46 |
|
51, 52 |
5, 10 |
1474.4 |
1480.6 |
0.42 |
|
53, 54 |
2, 12 |
1505.8 |
1507.5 |
0.11 |
|
55, 56 |
3, 12 |
1534.3 |
1536.6 |
0.15 |
|
57, 58 |
5, 11 |
1570.6 |
1576.5 |
0.38 |
|
59, 60 |
5, 8 |
1584.6 |
1591.9 |
0.46 |
|
61, 62 |
4, 12 |
1603.7 |
1607.1 |
0.21 |
|
63, 64 |
5, 12 |
1735.5 |
1741.2 |
0.33 |
|
65, 66 |
2, 13 |
1768.5 |
1770.3 |
0.10 |
|
67, 68 |
3, 13 |
1793.5 |
1795.9 |
0.13 |
|
69, 70 |
6, 10 |
1837.2 |
1848.0 |
0.59 |
|
71, 72 |
5, 7 |
1842.3 |
1850.1 |
0.42 |
|
73, 74 |
6, 11 |
1844.3 |
1854.3 |
0.54 |
|
75, 76 |
4, 13 |
1849.2 |
1852.7 |
0.19 |
|
77, 78 |
4, 5 |
1892.8 |
1897.7 |
0.26 |
|
79, 80 |
6, 12 |
1942.4 |
1951.9 |
0.49 |
|
81, 82 |
6, 9 |
1942.8 |
1954.3 |
0.59 |
|
83, 84 |
5, 13 |
1951.0 |
1956.7 |
0.29 |
|
85, 86 |
2, 14 |
2052.3 |
2054.1 |
0.09 |
|
87, 88 |
3, 14 |
2075.2 |
2077.7 |
0.12 |
|
89, 90 |
6, 13 |
2111.1 |
2120.1 |
0.43 |
|
91, 92 |
4, 14 |
2122.7 |
2126.3 |
0.17 |
|
93, 94 |
3, 3 |
2137.0 |
2140.0 |
0.14 |
|
95, 96 |
6, 8 |
2181.3 |
2193.4 |
0.55 |
|
97, 98 |
5, 14 |
2205.6 |
2211.2 |
0.25 |
|
99, 100 |
7, 11 |
2199.6 |
2215.4 |
0.72 |
|
101, 102 |
7, 12 |
2223.0 |
2237.8 |
0.67 |
|
103, 104 |
5, 6 |
2275.4 |
2283.7 |
0.36 |
|
105, 106 |
7, 10 |
2281.7 |
2298.3 |
0.73 |
|
107, 108 |
7, 13 |
2333.3 |
2347.3 |
0.60 |
|
109, 110 |
6, 14 |
2333.8 |
2342.5 |
0.37 |
|
111, 112 |
2, 15 |
2357.2 |
2358.9 |
0.07 |
|
113, 114 |
3, 15 |
2378.9 |
2381.2 |
0.10 |
|
115, 116 |
4, 15 |
2421.3 |
2424.8 |
0.14 |
|
117, 118 |
7, 9 |
2485.9 |
2503.2 |
0.70 |
|
119, 120 |
5, 15 |
2492.0 |
2497.5 |
0.22 |
|
121, 122 |
7, 14 |
2512.8 |
2526.3 |
0.54 |
|
123, 124 |
8, 12 |
2565.0 |
2586.6 |
0.84 |
|
125, 126 |
6, 7 |
2574.4 |
2586.9 |
0.49 |
|
127, 128 |
6, 15 |
2598.7 |
2607.3 |
0.33 |
|
129,130 |
8, 13 |
2613.1 |
2633.7 |
0.79 |
|
131, 132 |
8, 11 |
2614.4 |
2637.0 |
0.86 |
|
133, 134 |
4, 4 |
2630.0 |
2635.4 |
0.21 |
|
135, 136 |
2, 16 |
2683.2 |
2684.5 |
0.05 |
|
137, 138 |
3, 16 |
2704.1 |
2706.1 |
0.07 |
|
139, 140 |
8, 14 |
2742.8 |
2762.4 |
0.71 |
|
141, 142 |
4, 16 |
2743.2 |
2746.5 |
0.12 |
|
143, 144 |
7, 15 |
2747.0 |
2759.9 |
0.47 |
|
145, 146 |
8, 10 |
2776.0 |
2799.3 |
0.84 |
|
147, 148 |
5, 16 |
2806.0 |
2811.3 |
0.19 |
|
149, 150 |
2, 1 |
2832.3 |
2835.3 |
0.11 |
Замечания: При аналитическом решении собственные частоты колебаний ω круговой цилиндрической оболочки, свободно опертой по торцам, с плотностью материала ρ могут быть определены из характеристического уравнения:
\[\left( {\frac{4\cdot \pi^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)^{3}\cdot \omega^{6}+K2\cdot \left( {\frac{4\cdot \pi ^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)^{2}\cdot \omega^{4}+K1\cdot \left( {\frac{4\cdot \pi^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)\cdot \omega ^{2}+K0=0, \quad где:\quad \] \[ K2=-1-\frac{1}{2}\cdot \left( {3-\nu } \right)\cdot \left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]-\frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}+2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right\} \] \[ {\begin{array}{*{20}c} {K1=\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}+\frac{1}{2}\cdot \left( {3-\nu -2\cdot \nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot n^{2}+} \\ {\frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\frac{1}{2}\cdot \left( {3-\nu } \right)\cdot \left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{3}} \right.+2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}-\left( {2-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}\cdot n^{2}-\frac{1}{2}\left( {3+\nu } \right)\cdot n^{4}+} \\ {\left. {2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right\} +\frac{h^{4}}{144\cdot R^{4}}\cdot \left\{ {2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{6}+\left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}\cdot n^{2}} \right\}} \\ \end{array} } \] \[ {\begin{array}{*{20}c} {K0=-\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}-\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{4}-2\cdot \left( {4-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}\cdot n^{2}-} \right.} \\ {\left. {8\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}\cdot n^{4}-2\cdot n^{6}+4\cdot \left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}+4\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}\cdot n^{2}+n^{4}} \right\} -} \\ {\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \frac{h^{4}}{144\cdot R^{4}}\cdot \left\{ {4\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{8}-4\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{6}\cdot n^{2}+\left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}\cdot n^{4}} \right\}} \\ \end{array} } \]
m=2,3,4, ... - число узловых линий в окружном направлении с учетом линий по торцевым опорным контурам,
n=0,1,2, ...- число пар узловых линий в меридиональном направлении при расположении каждой пары на одном диаметре.
