Свободные колебания круговой цилиндрической оболочки, защемленной по торцам
Цель: Модальный анализ круговой цилиндрической оболочки, защемленной по торцам.
Файл с исходными данными: 5.8_c.spr
Формулировка задачи: Определить собственные формы и частоты колебаний ω круговой цилиндрической оболочки, защемленной по торцам, с плотностью материала ρ.
Ссылки: И. А. Биргер, Я. Г. Пановко, Прочность, устойчивость, колебания, Справочник в трех томах, Том 3, Москва, Машиностроение, 1968, стр. 437.
В. С. Гонткевич, Собственные колебания ортотропных цилиндрических оболочек, Труды конференции по теории пластин и оболочек, Казань, КФАН, 1961.
Исходные данные:
| E = 1.96·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 7.70 т/м3 | - плотность материала; |
| h = 0.25·10-3 м | - толщина цилиндрической оболочки; |
| R = 0.076 м | - радиус срединной поверхности цилиндрической оболочки; |
| L = 0.305 м | - длина цилиндрической оболочки. |
Конечноэлементная модель: Расчетная схема – система общего вида, 6400 четырехузловых элементов оболочки типа 50. Сетка конечных элементов разбита с шагом 4.765625·10-3 м в меридиональном направлении (64 элемента) и с шагом 3.6º в окружном направлении (100 элементов). Обеспечение граничных условий на свободно опертых торцах достигается за счет наложения связей по направлениям всех линейных и угловых перемещений (степени свободы X, Y, Z, UX, UY, UZ). Распределенная масса задается преобразованием статической нагрузки от собственного веса цилиндрической оболочки: ow = γ∙h, где γ = ρ∙g = 75.537 кН/м3. Количество узлов в расчетной схеме – 6500.
Результаты решения в SCAD
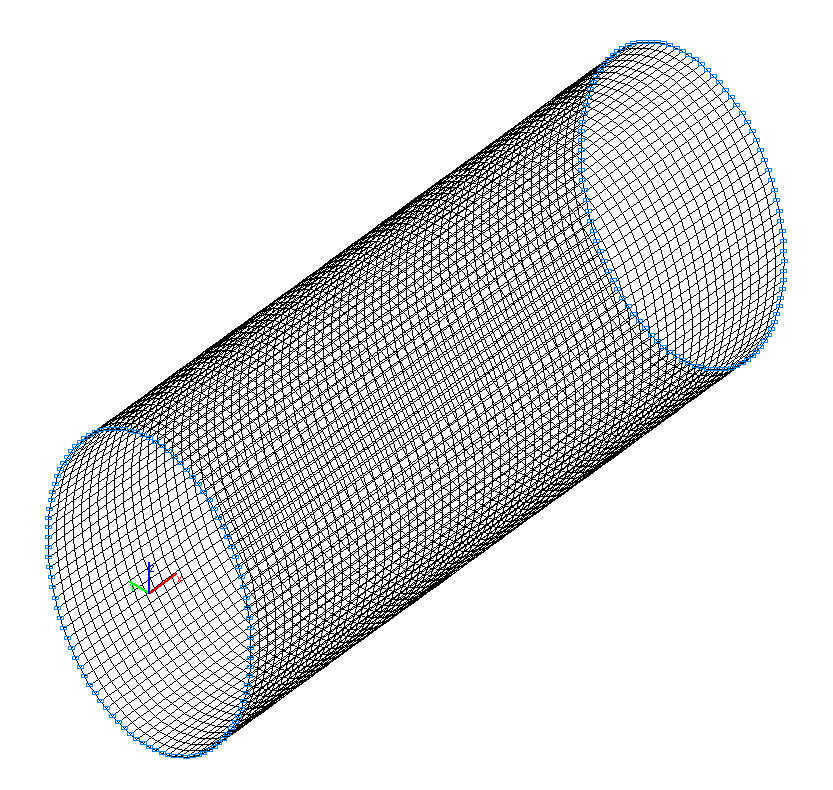
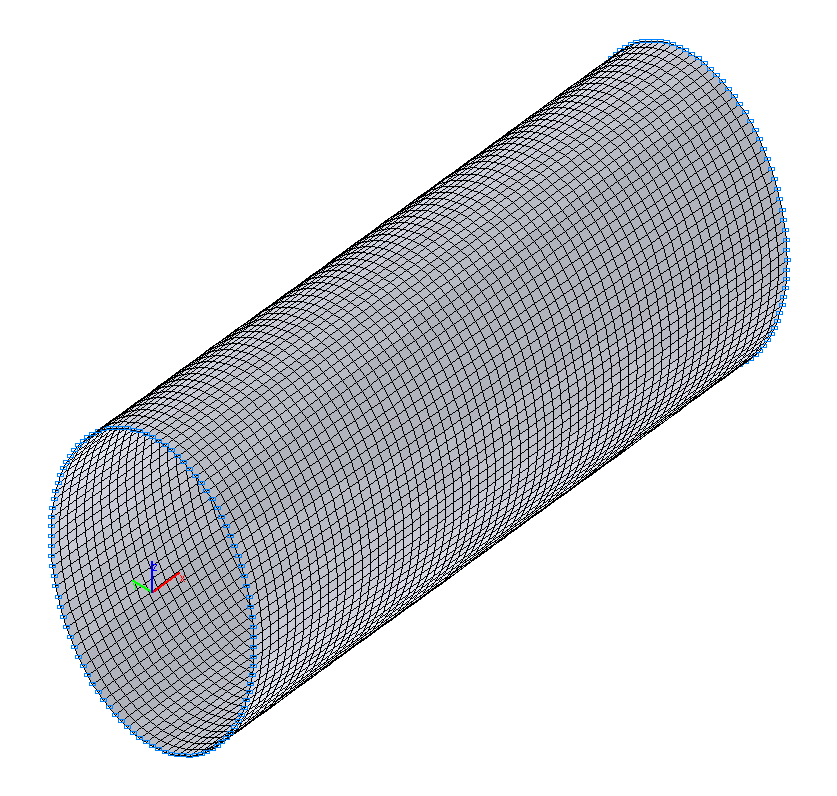
Расчетная схема
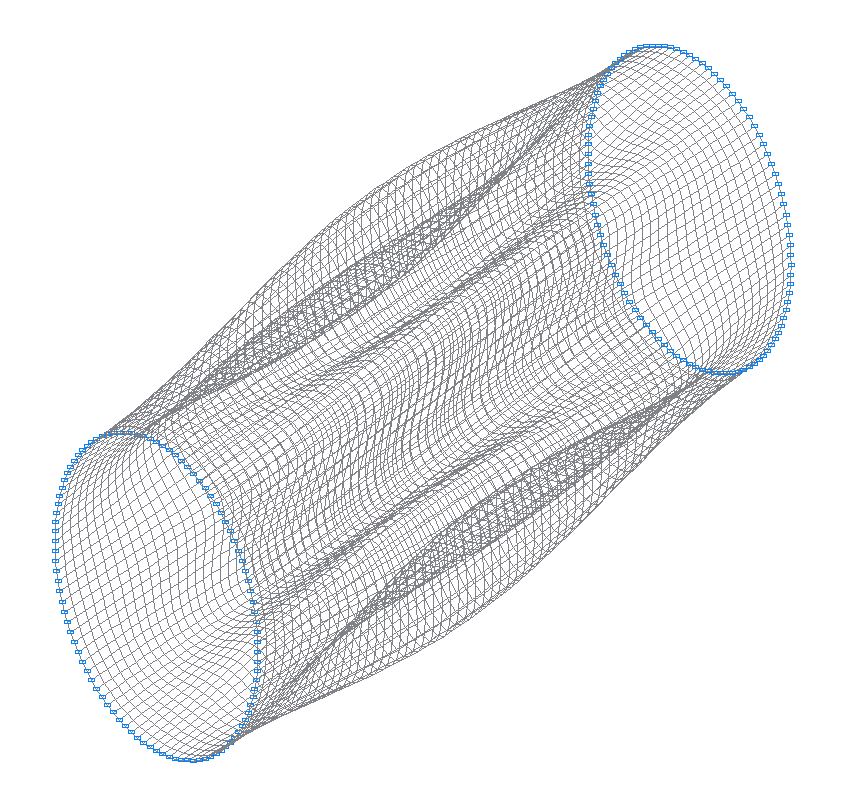

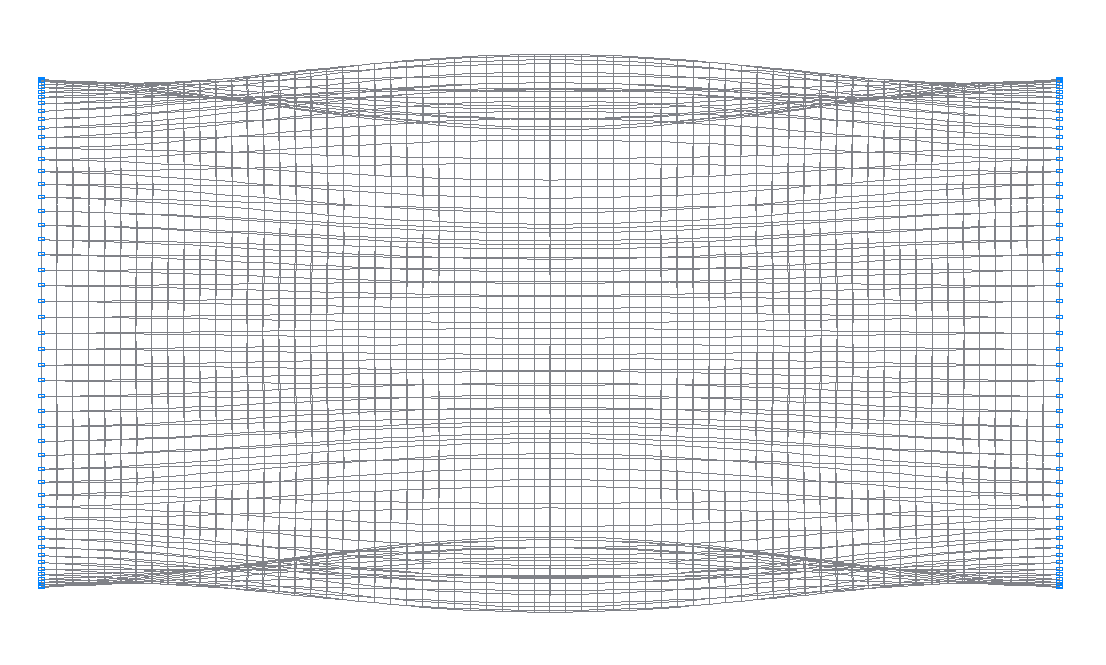
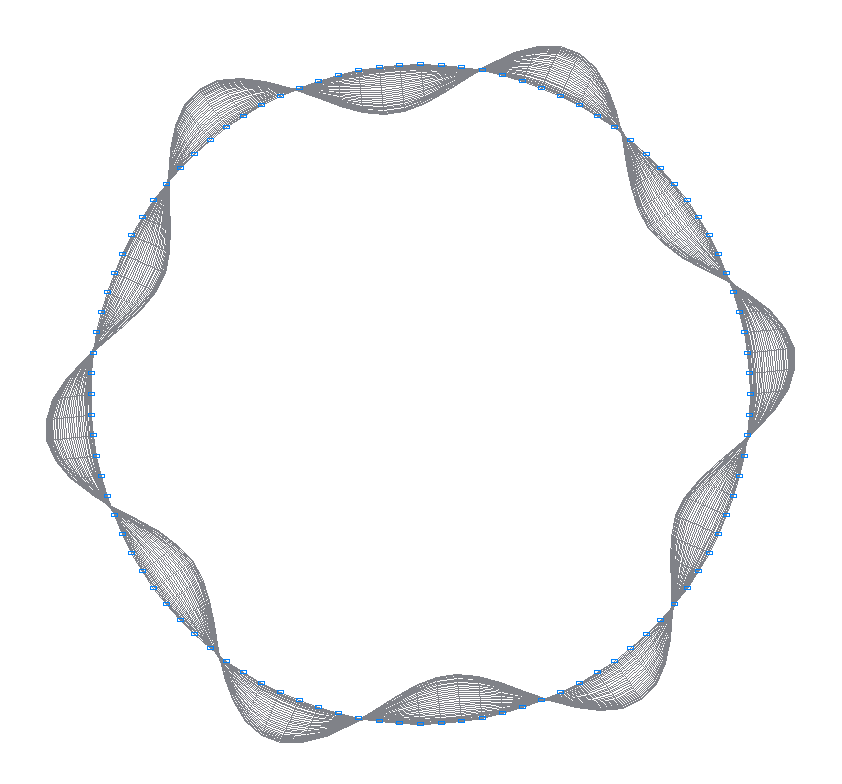
1-я (1-я теоретическая) собственная форма колебаний
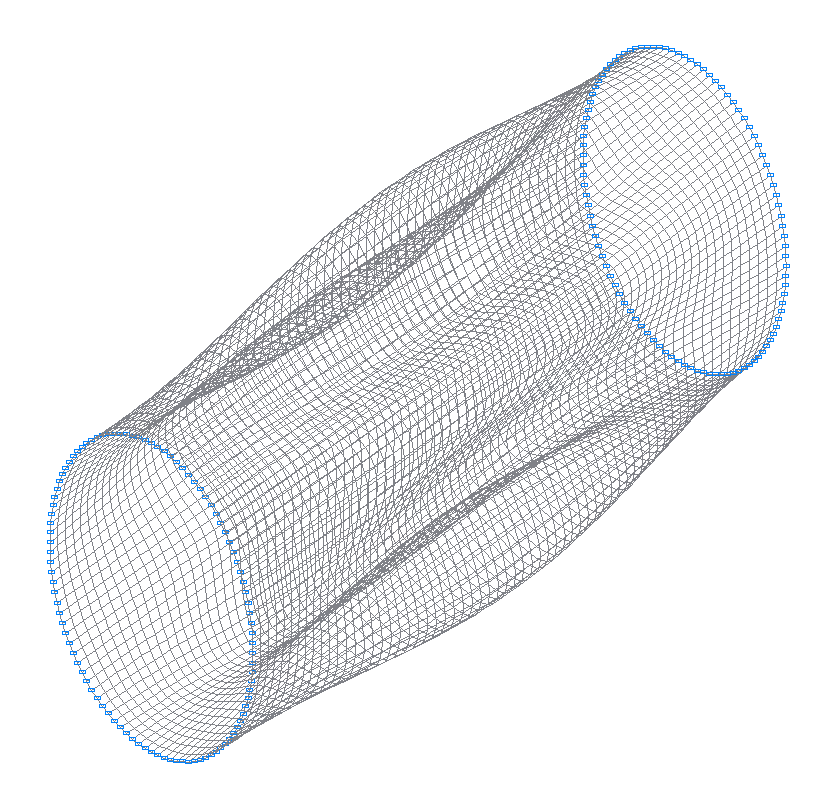


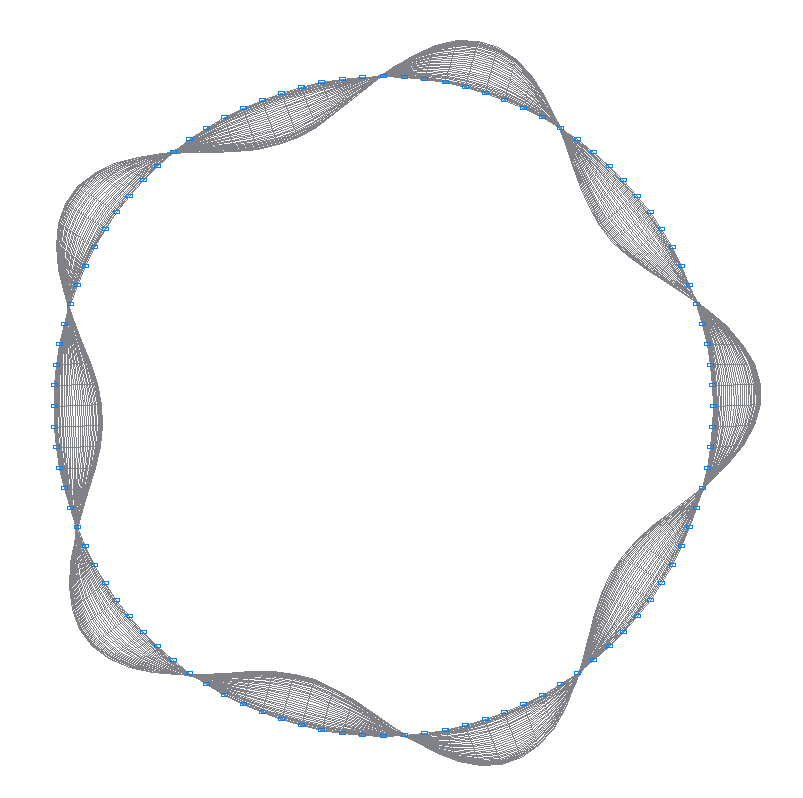
3-я (3-я теоретическая) собственная форма колебаний
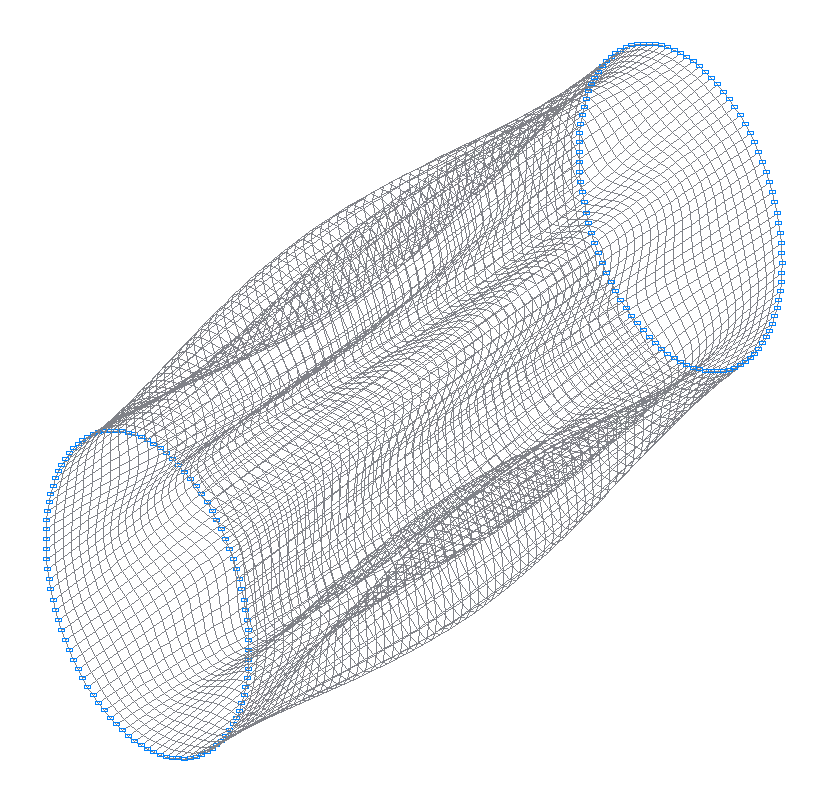

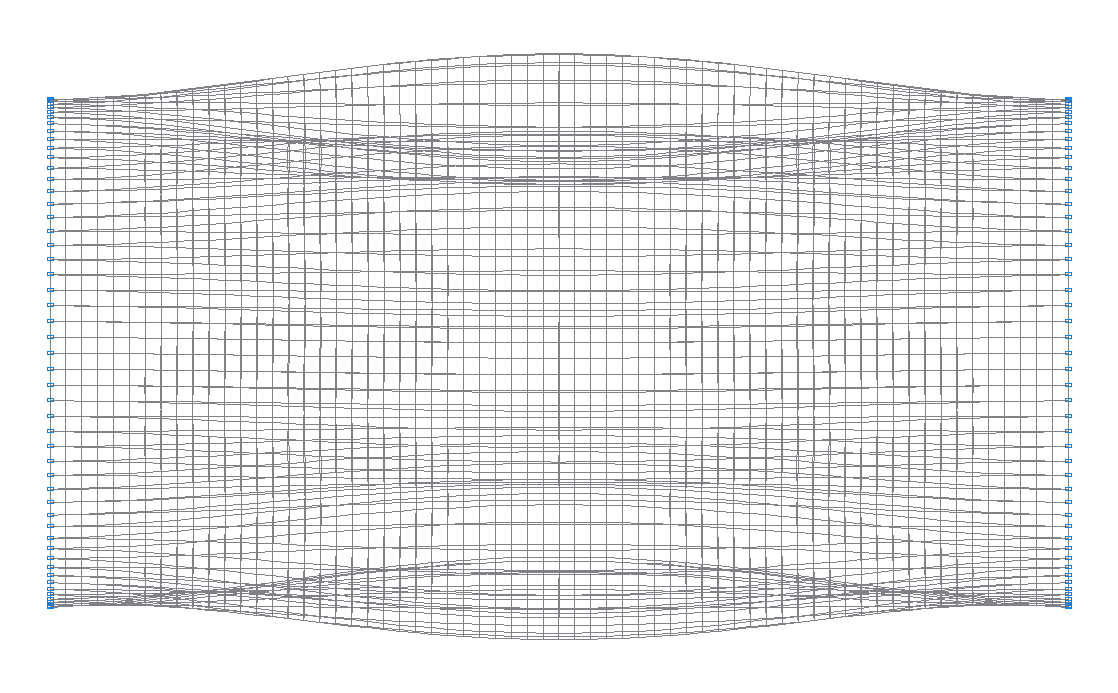
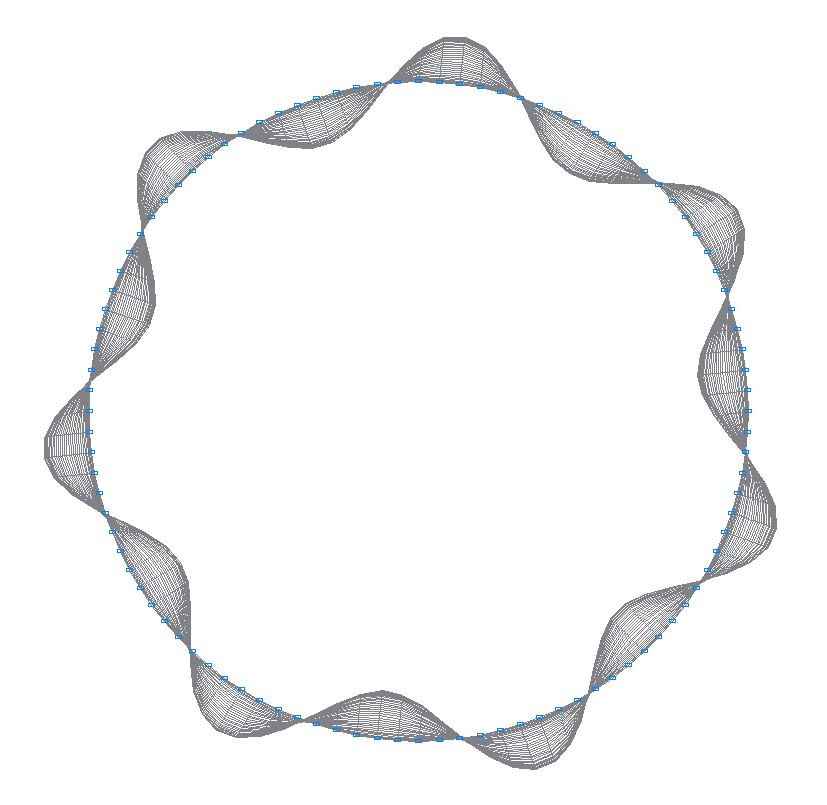
5-я (5-я теоретическая) собственная форма колебаний
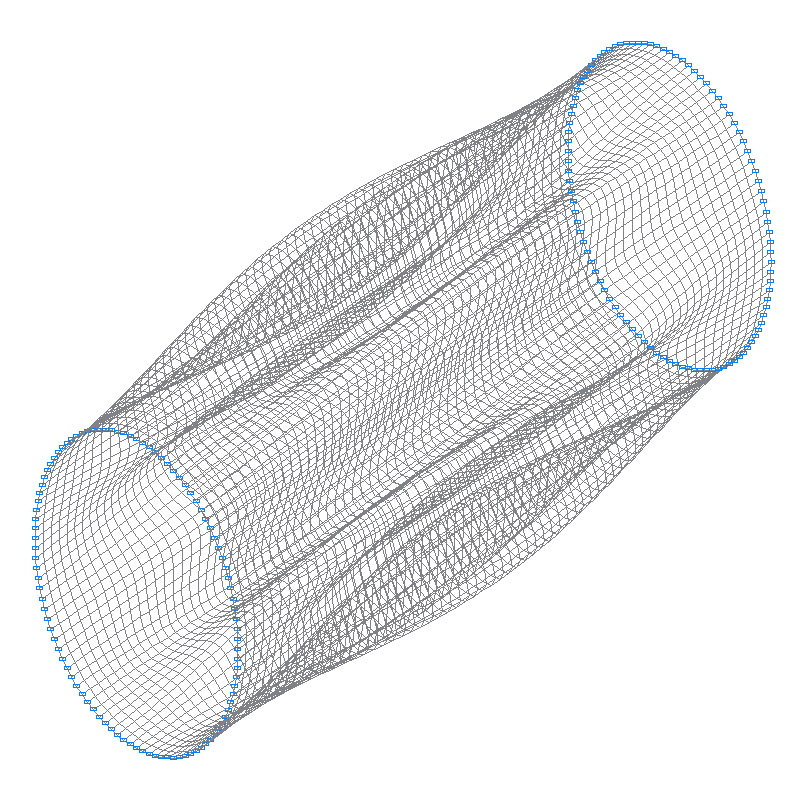

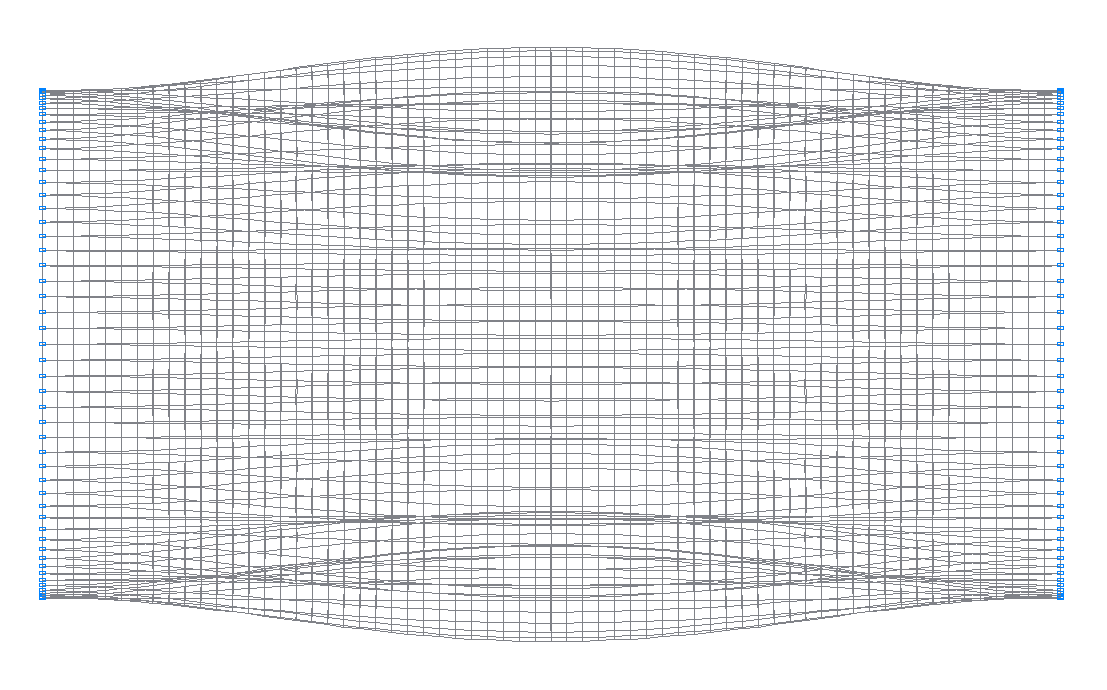
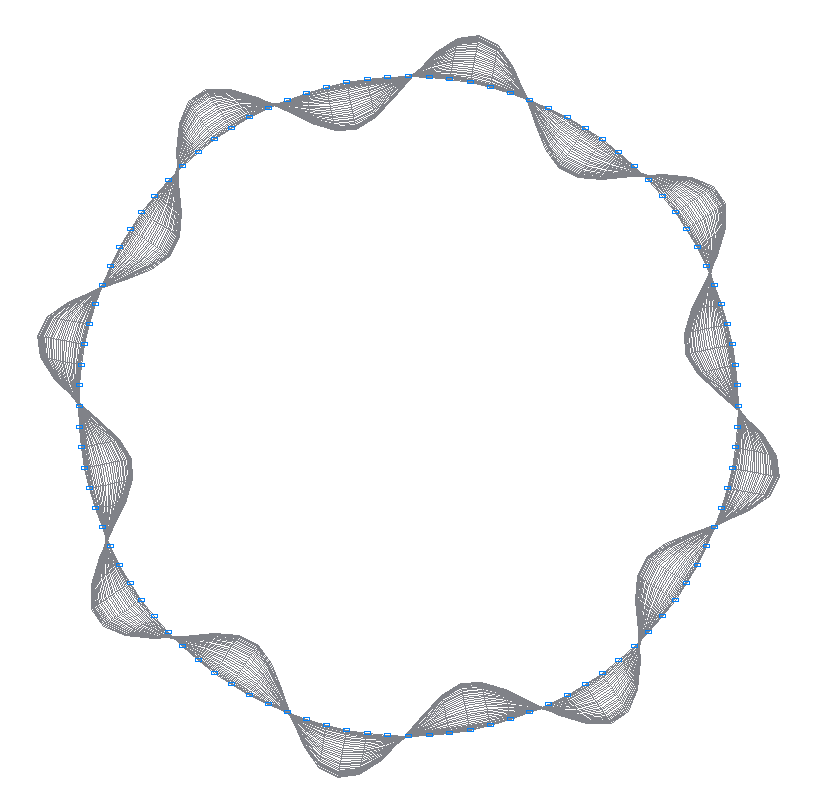
7-я (7-я теоретическая) собственная форма колебаний
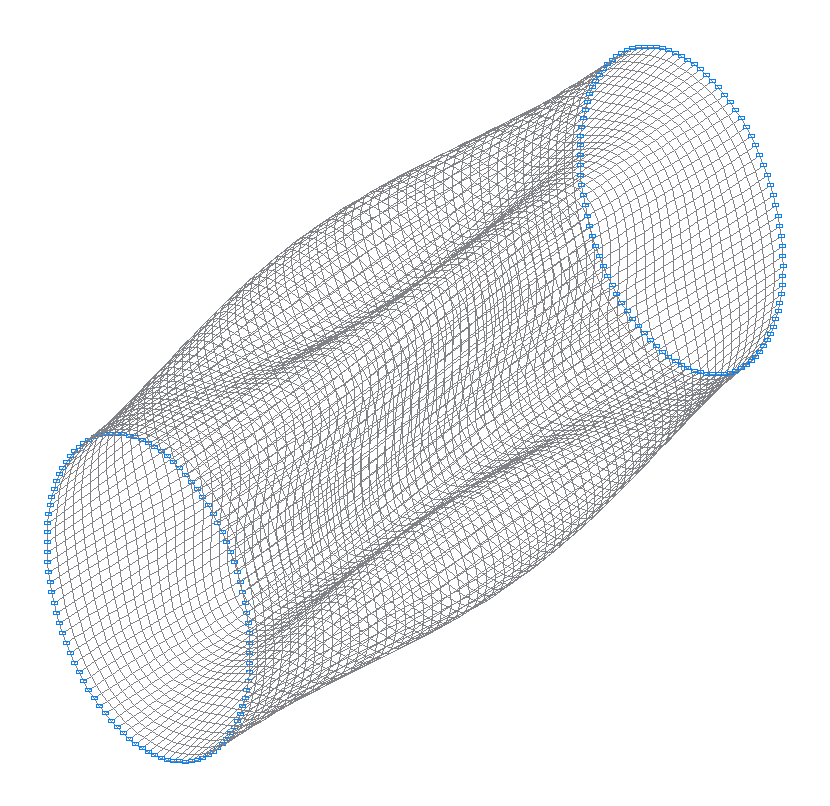

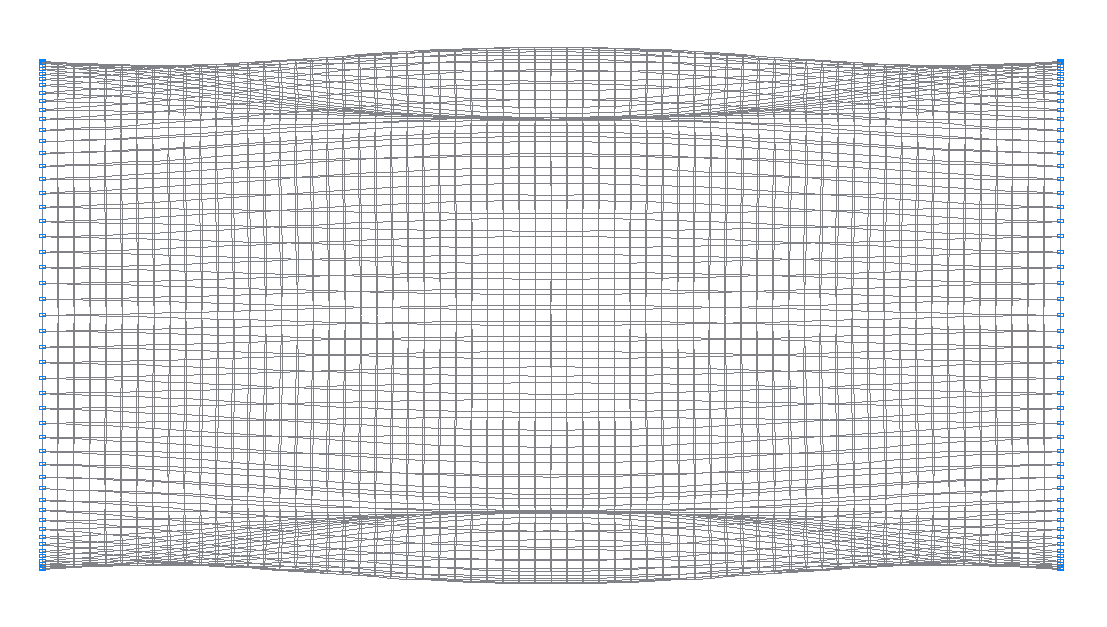
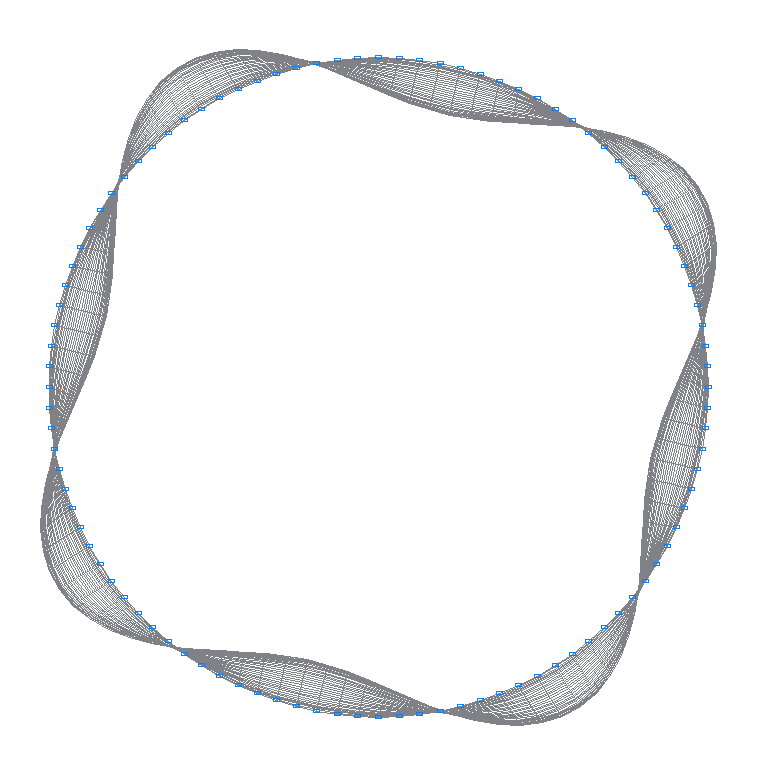
9-я (9-я теоретическая) собственная форма колебаний
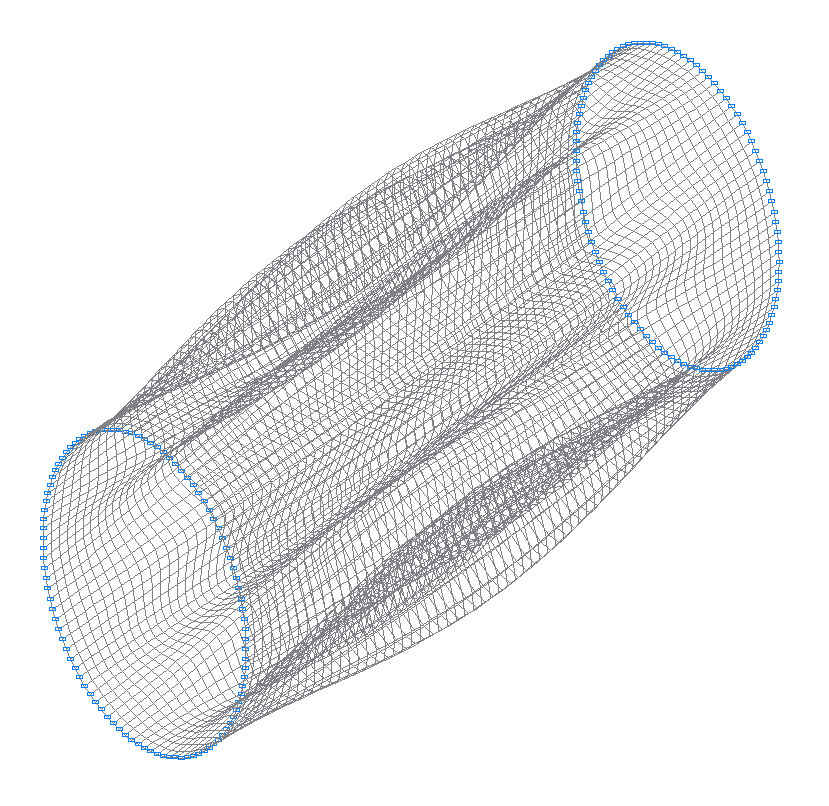

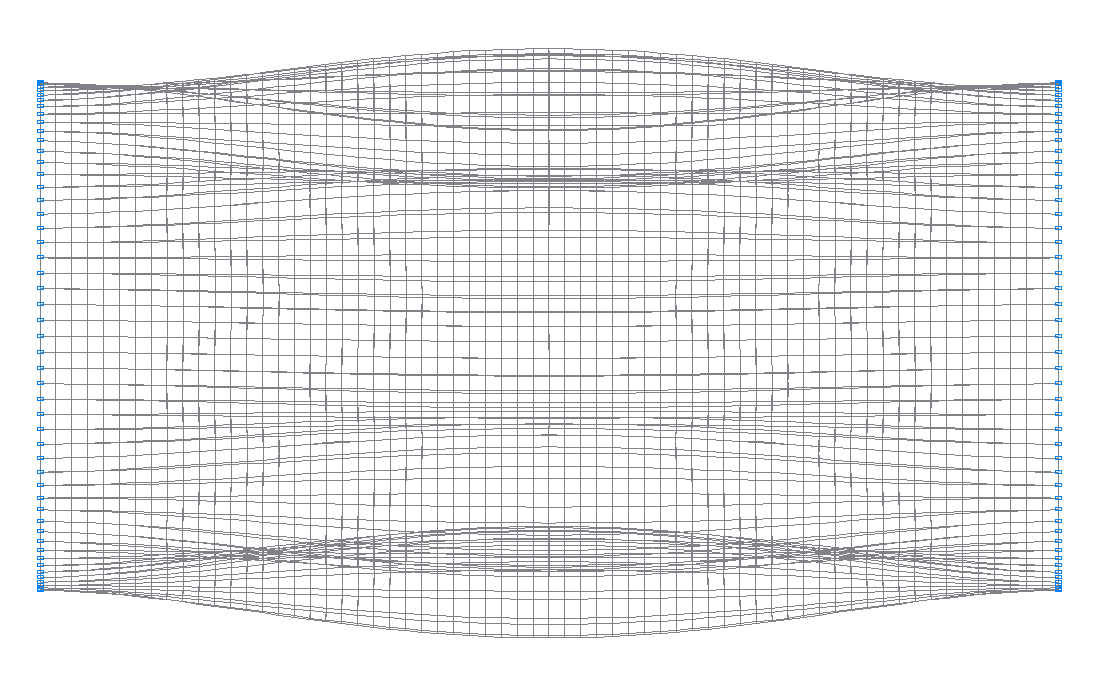
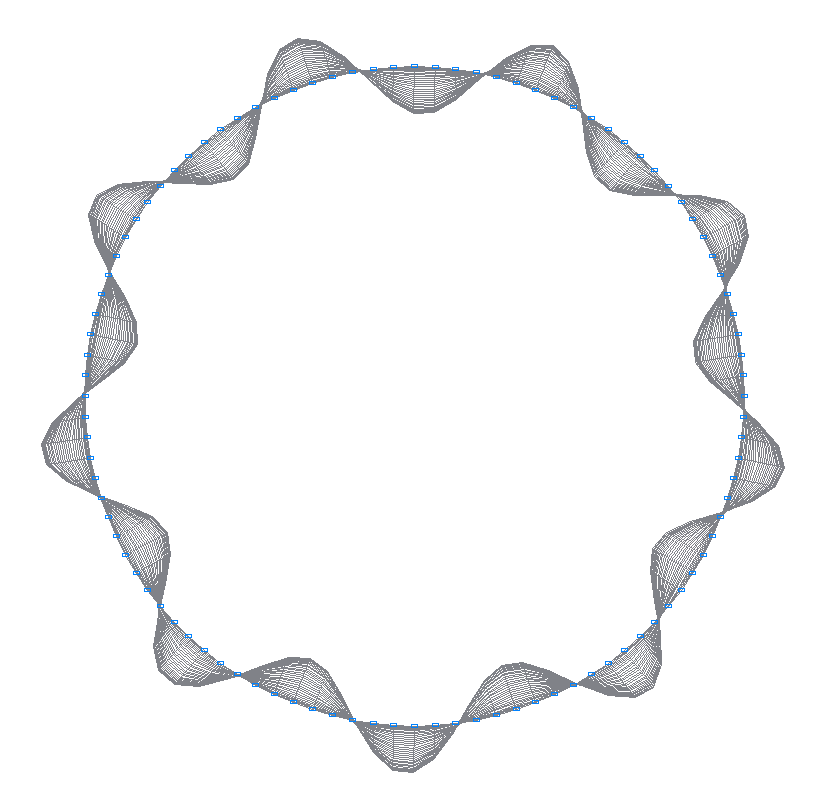
11-я (11-я теоретическая) собственная форма колебаний
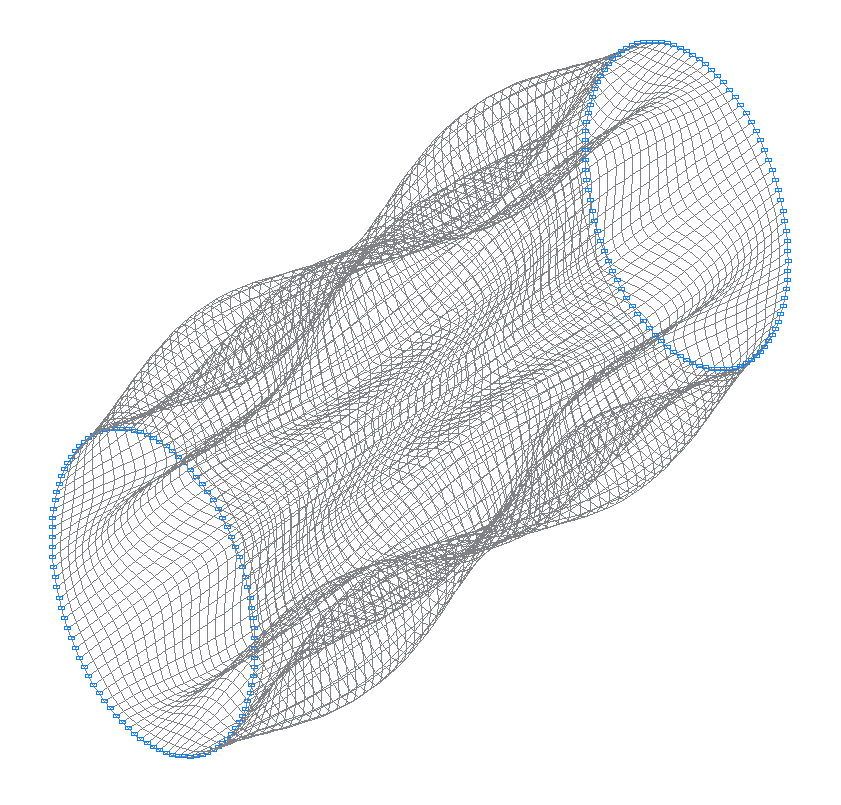

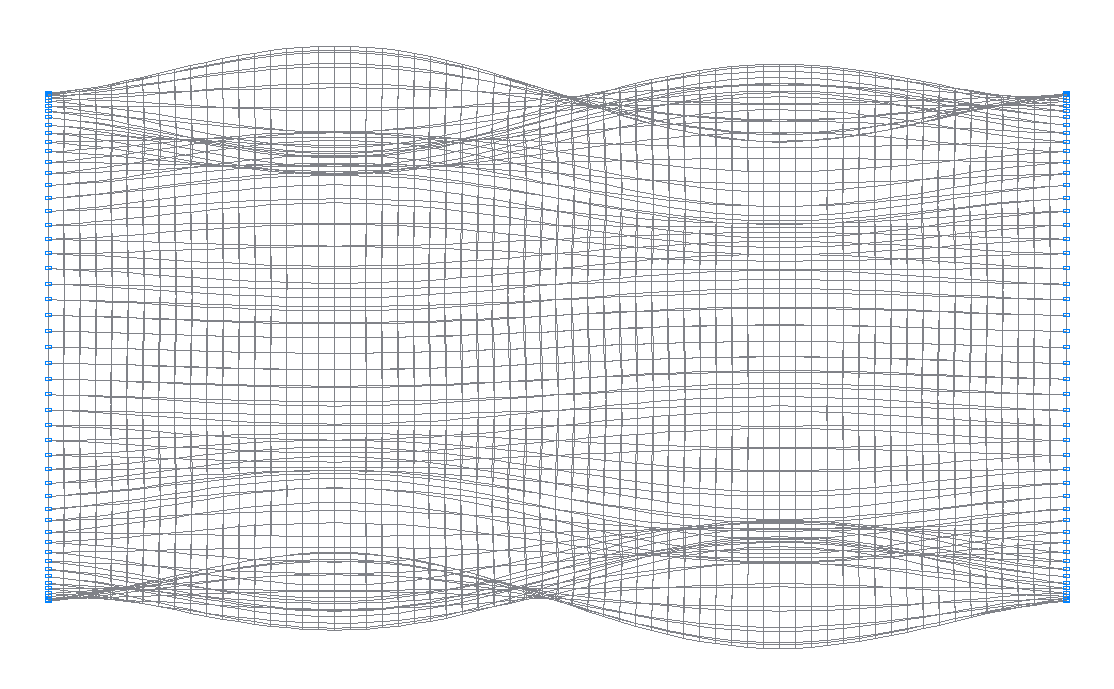

13-я (13-я теоретическая) собственная форма колебаний
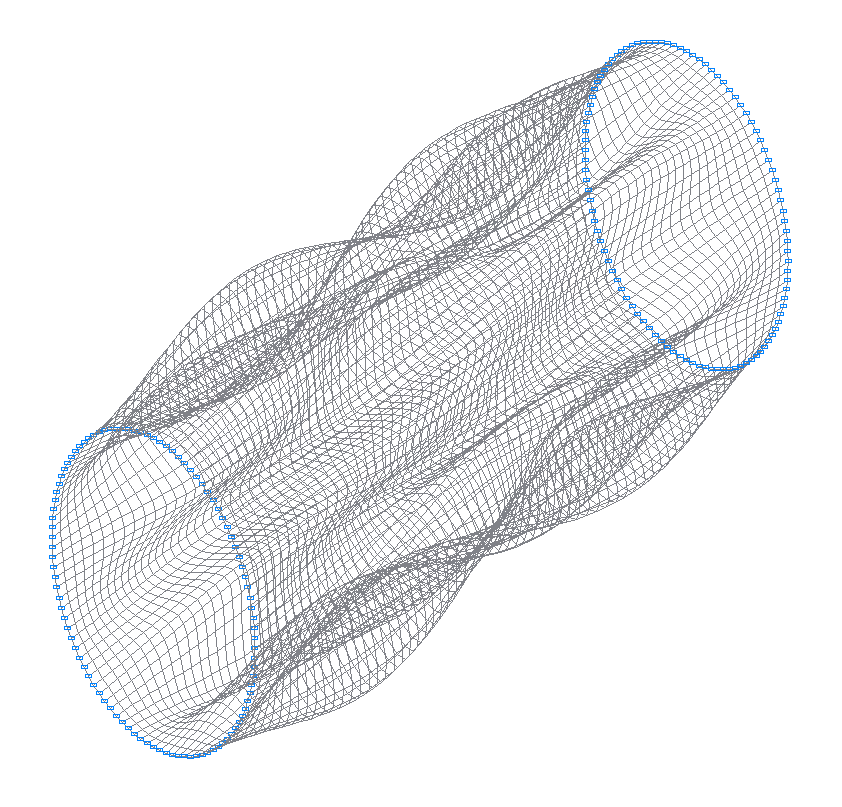
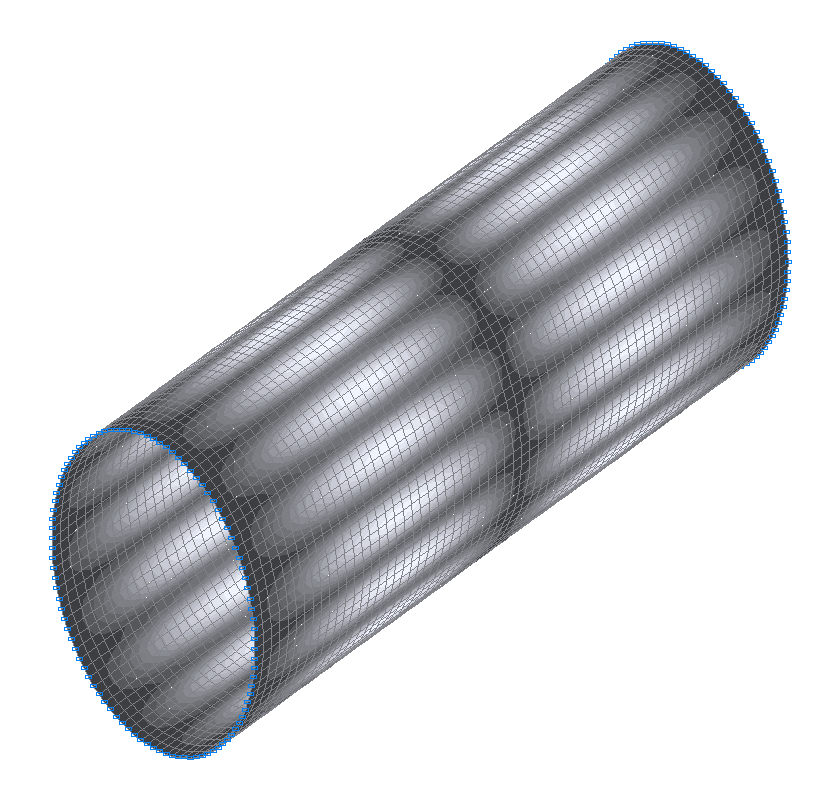
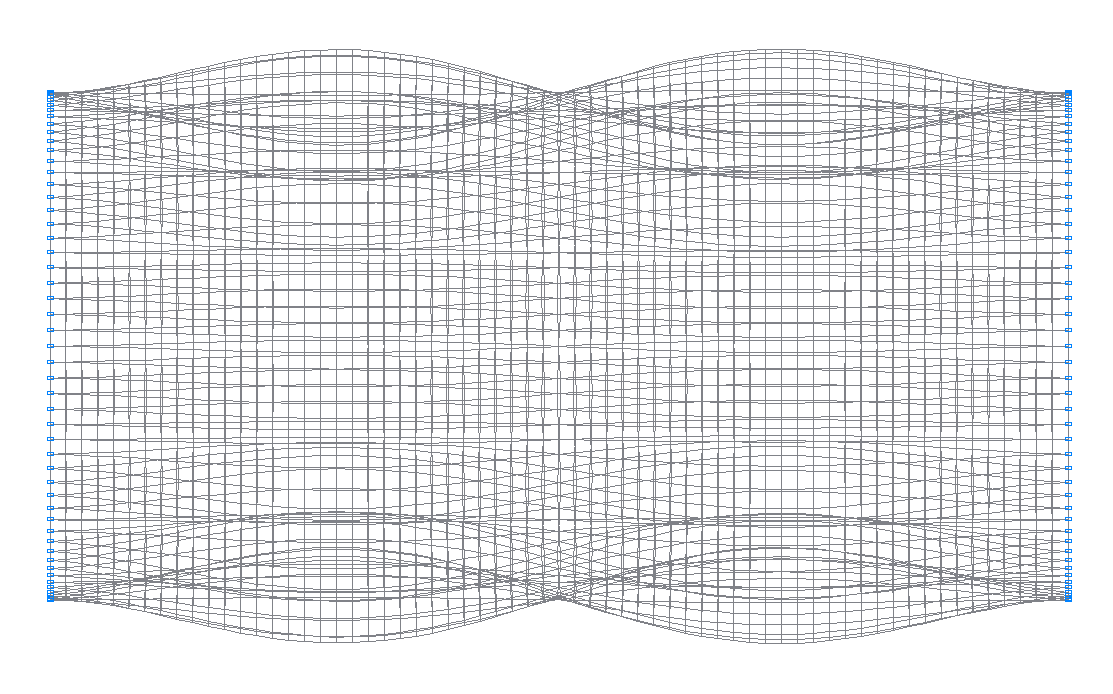

15-я (15-я теоретическая) собственная форма колебаний
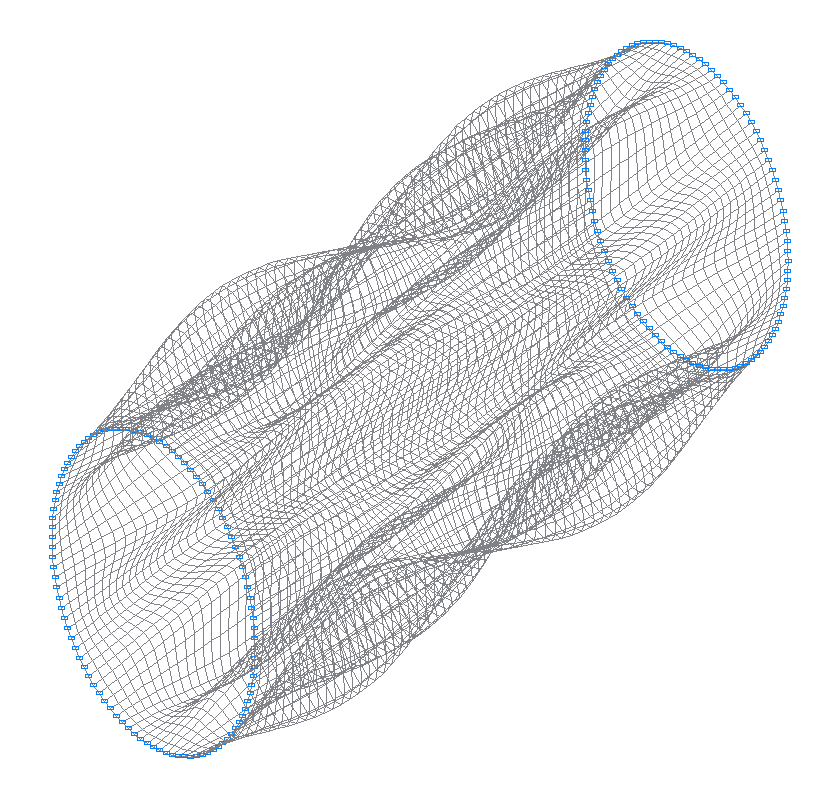


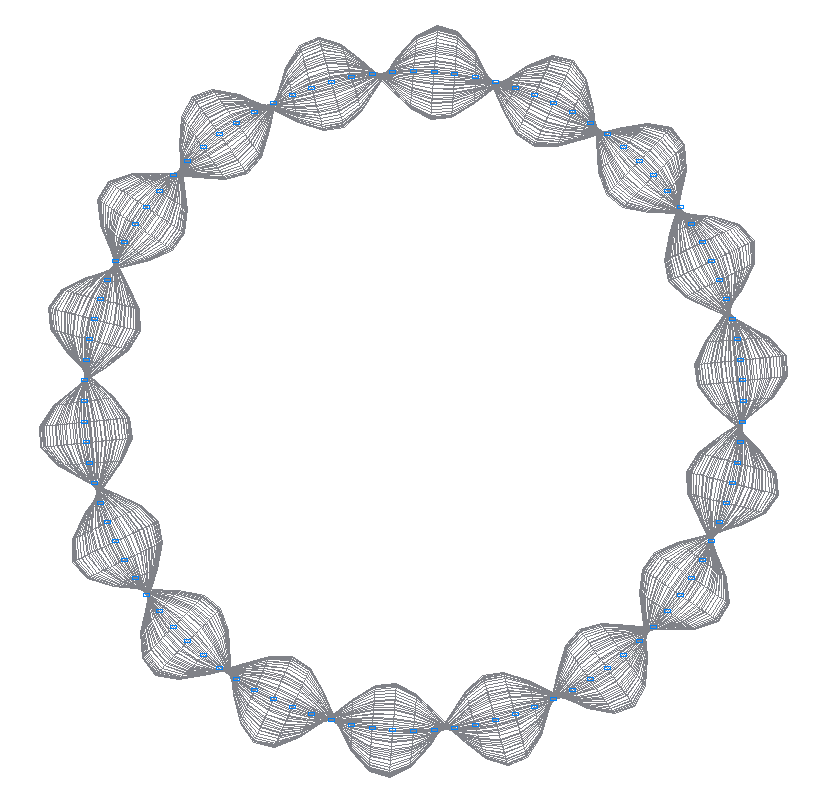
17-я (17-я теоретическая) собственная форма колебаний
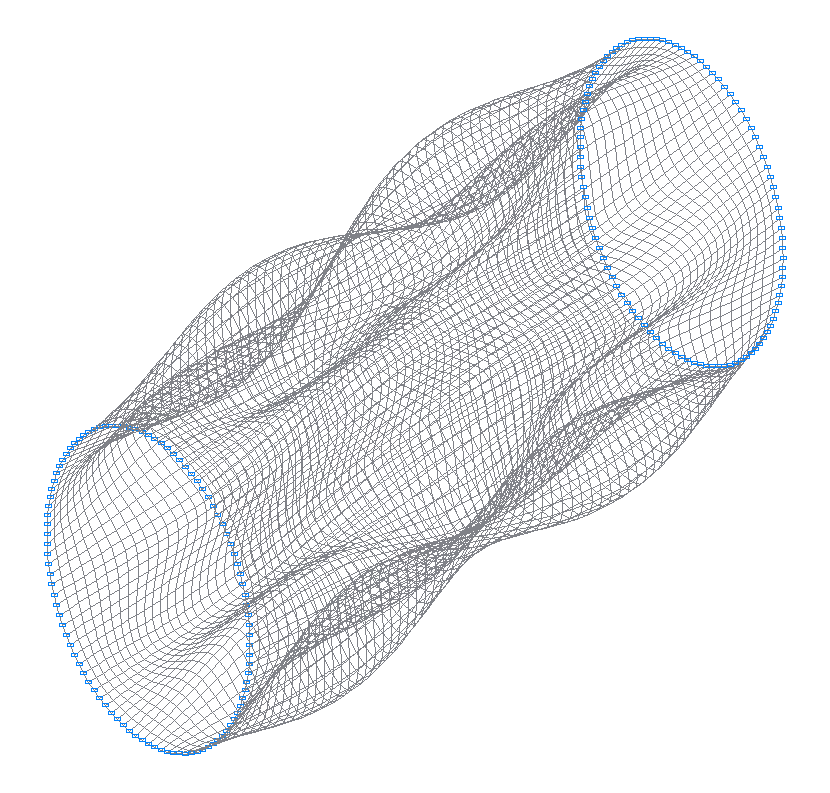


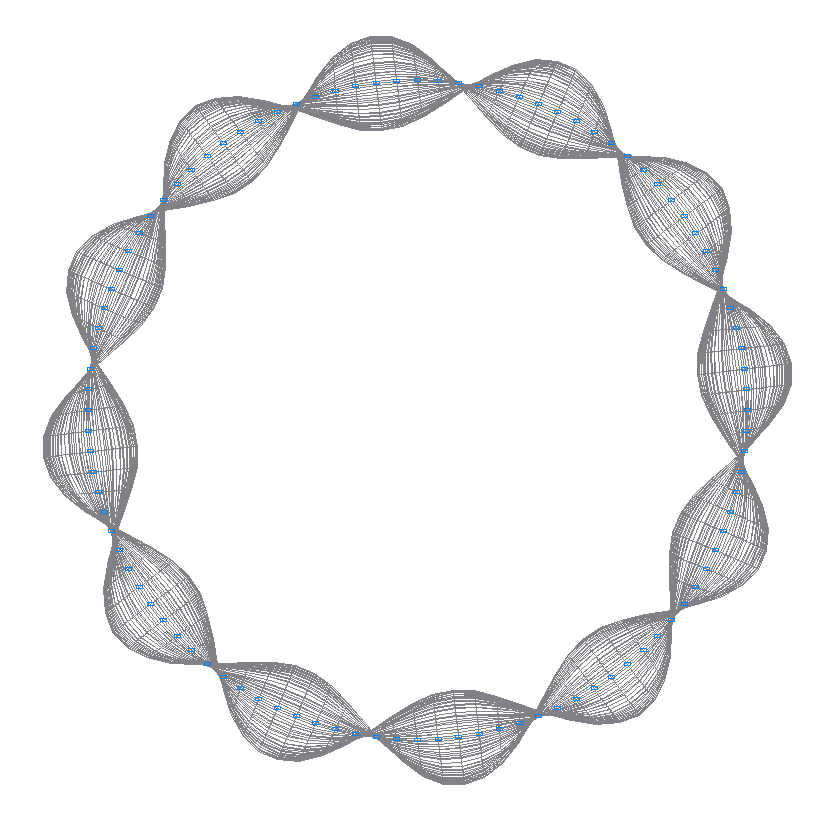
19-я (19-я теоретическая) собственная форма колебаний
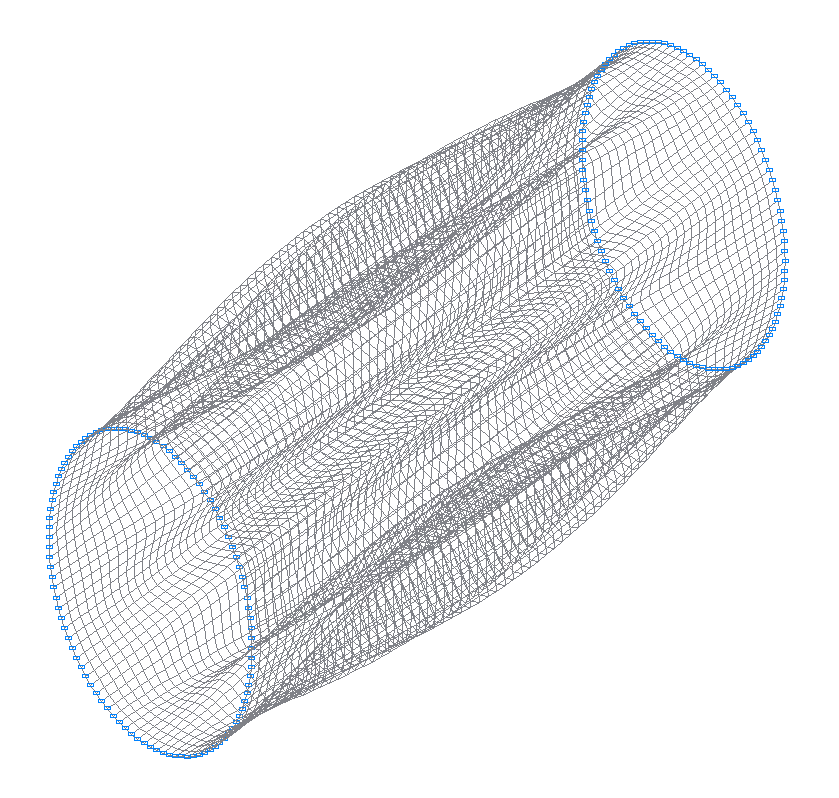

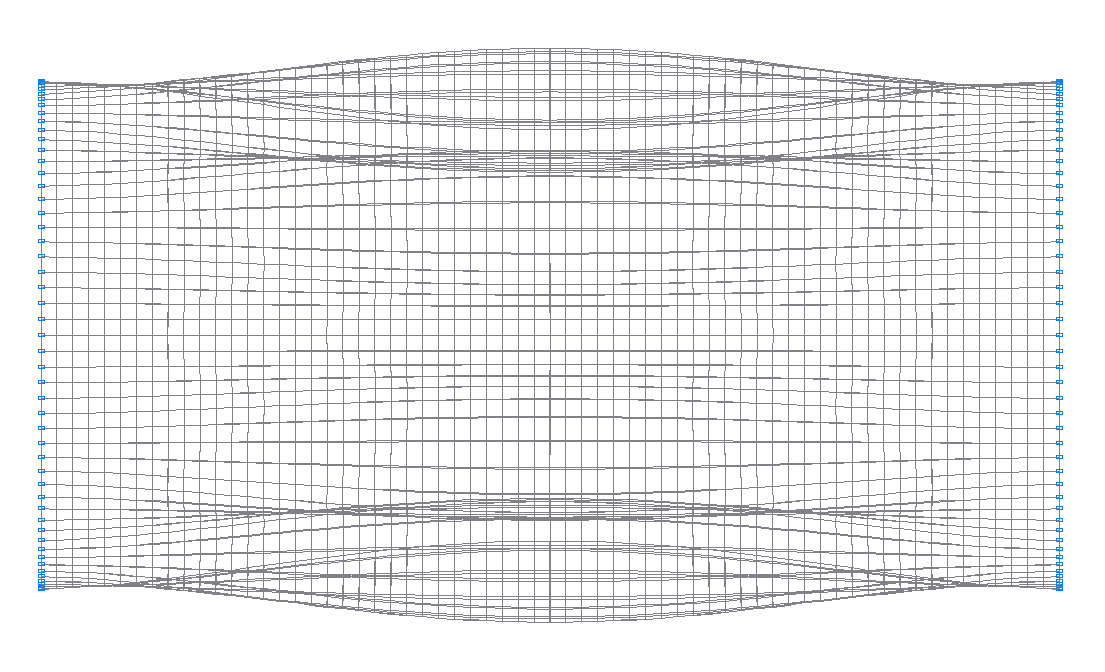
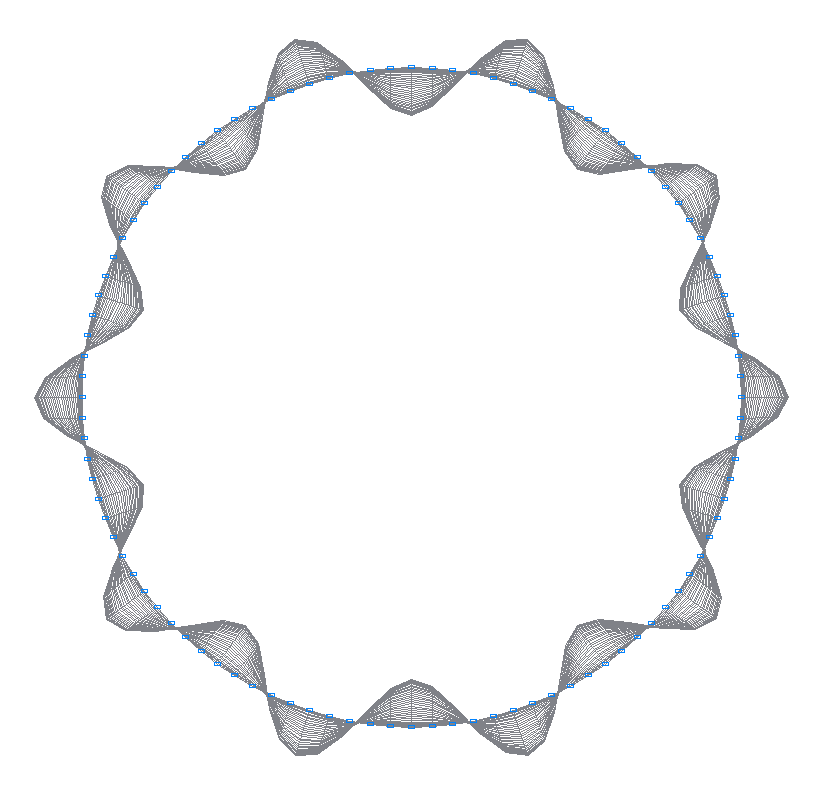
21-я (21-я теоретическая) собственная форма колебаний
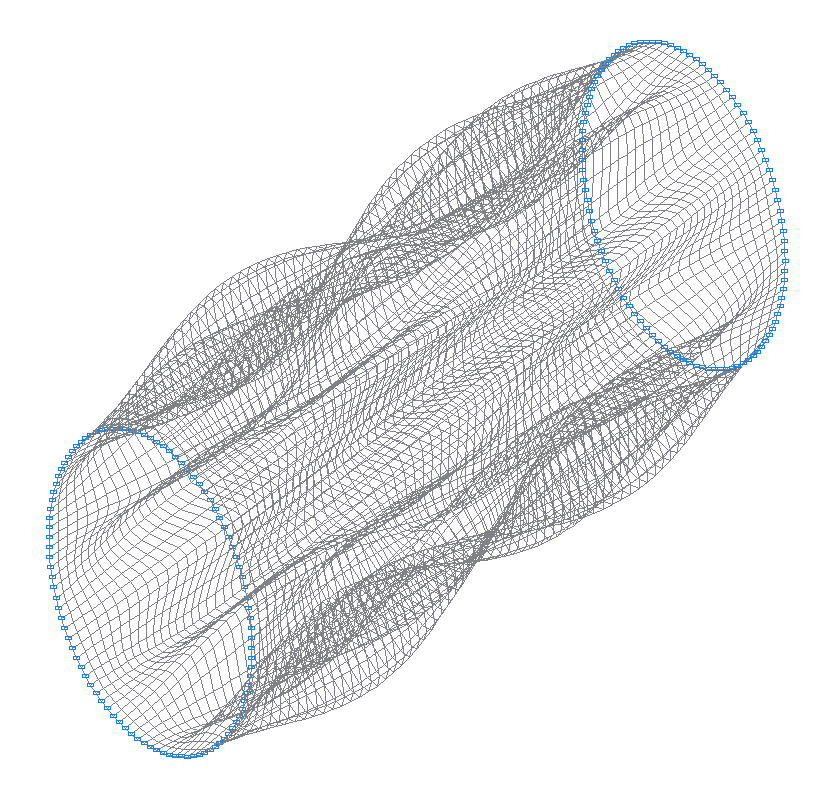
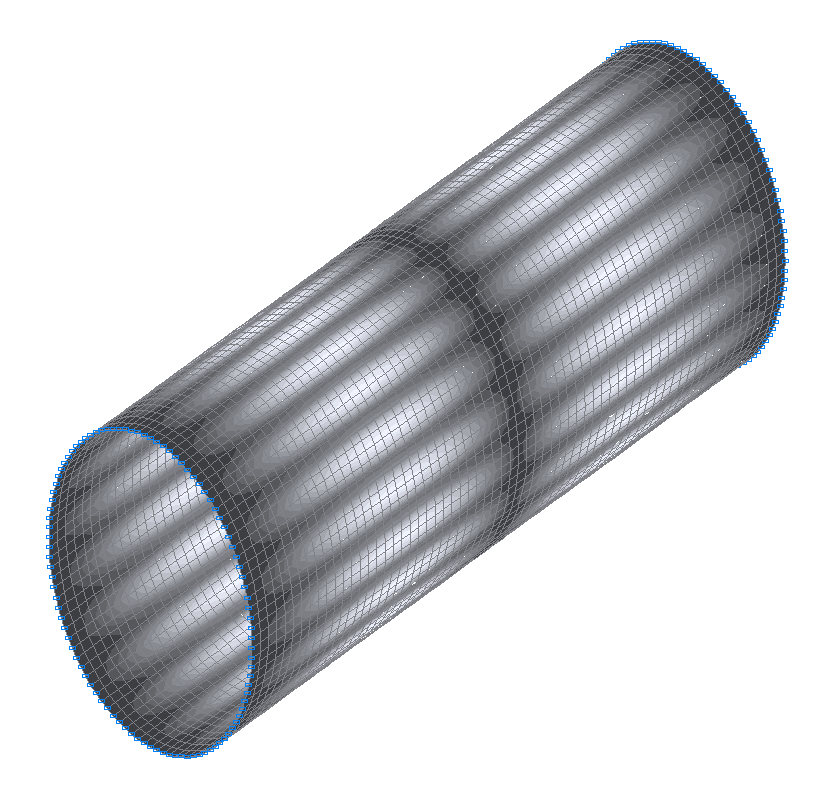

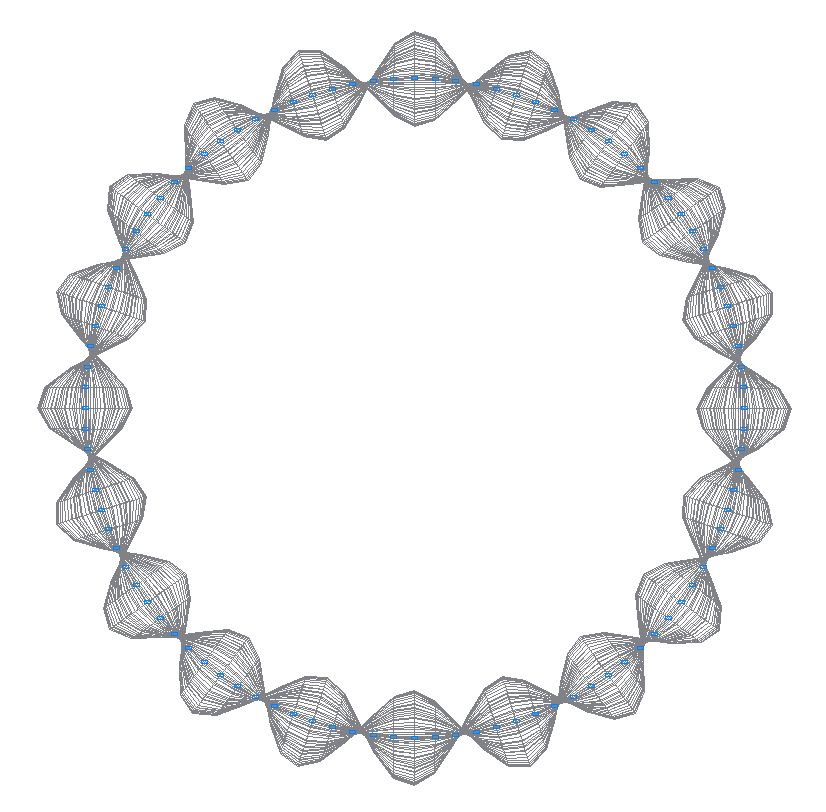
23-я (25-я теоретическая) собственная форма колебаний
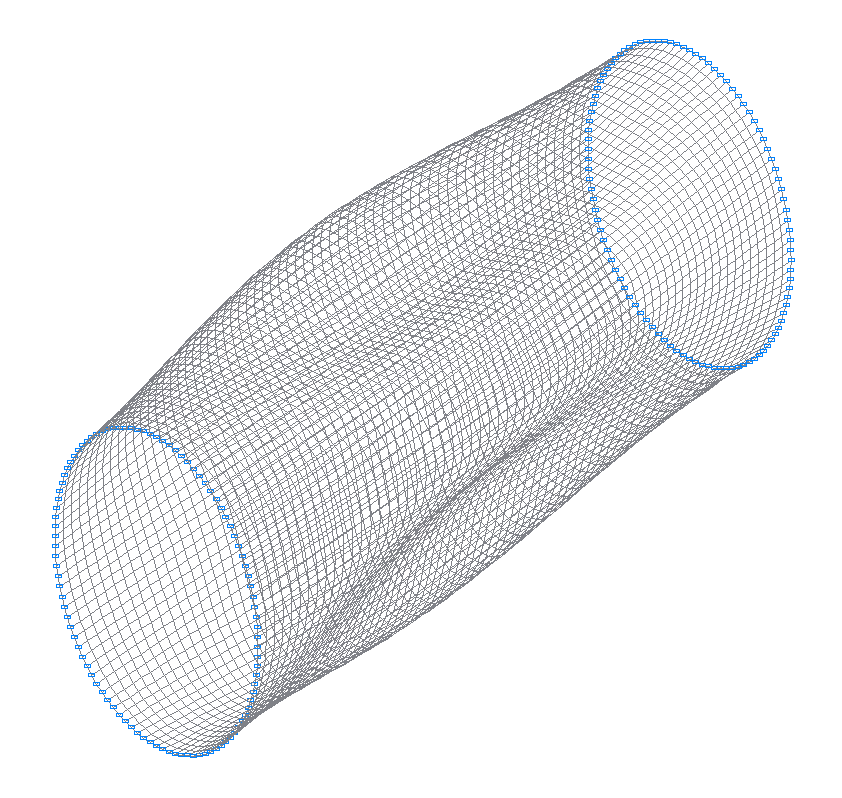

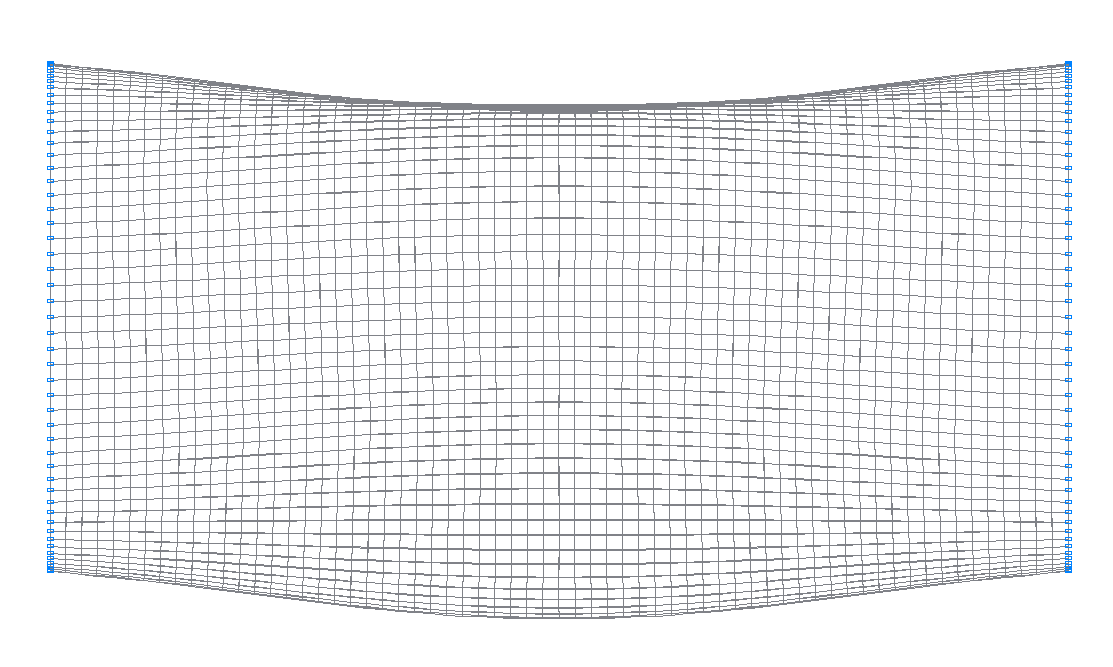
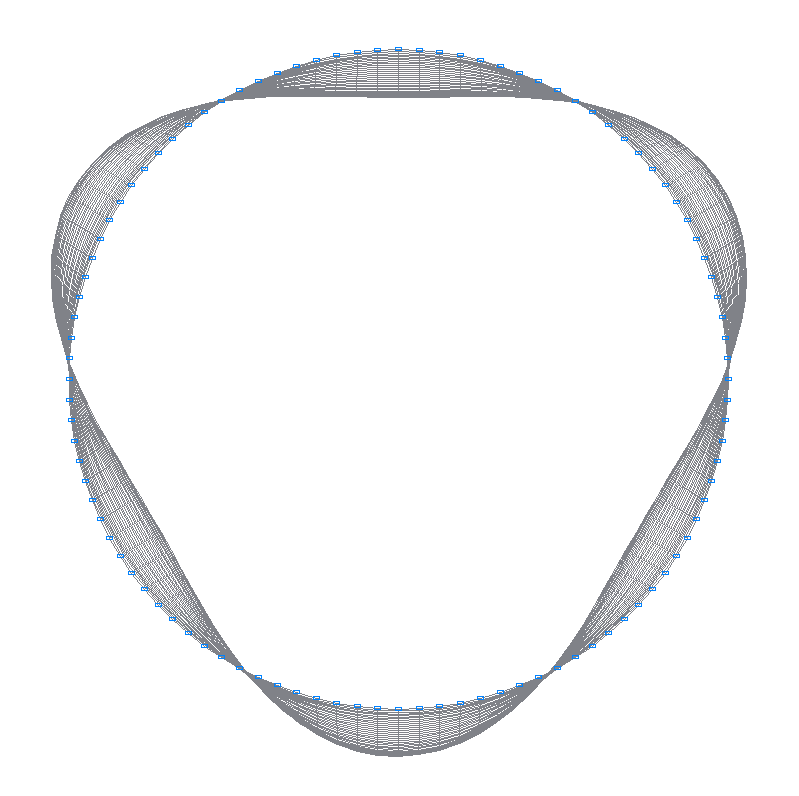
25-я (23-я теоретическая) собственная форма колебаний
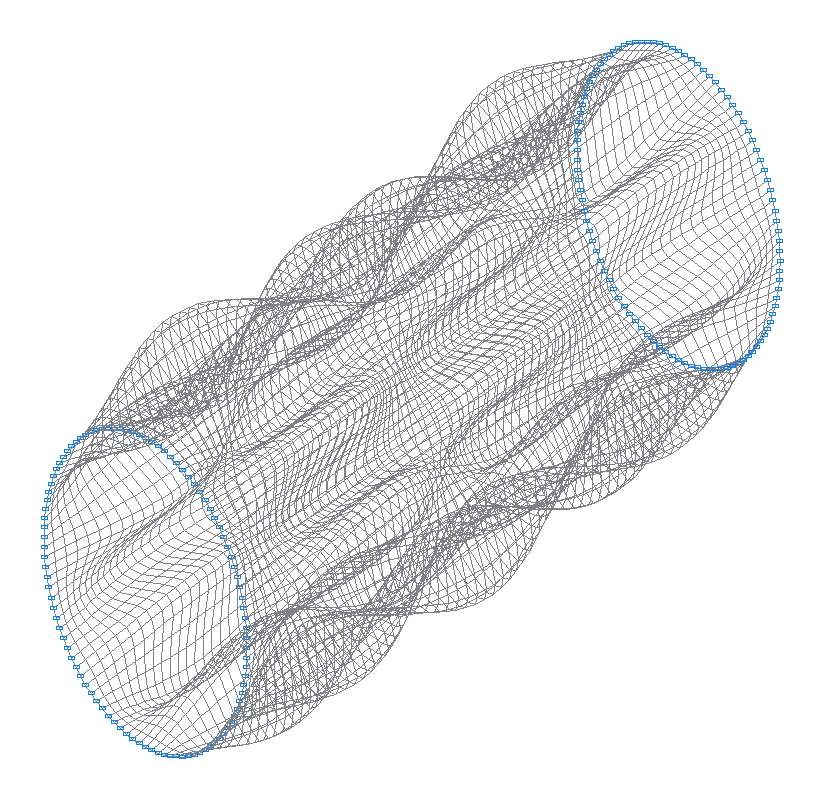
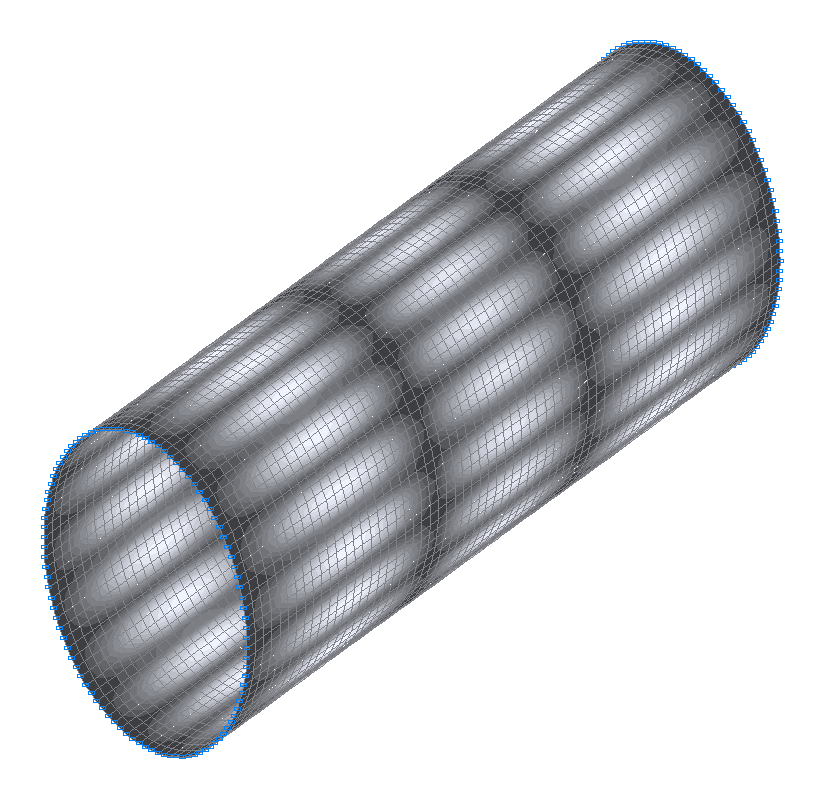
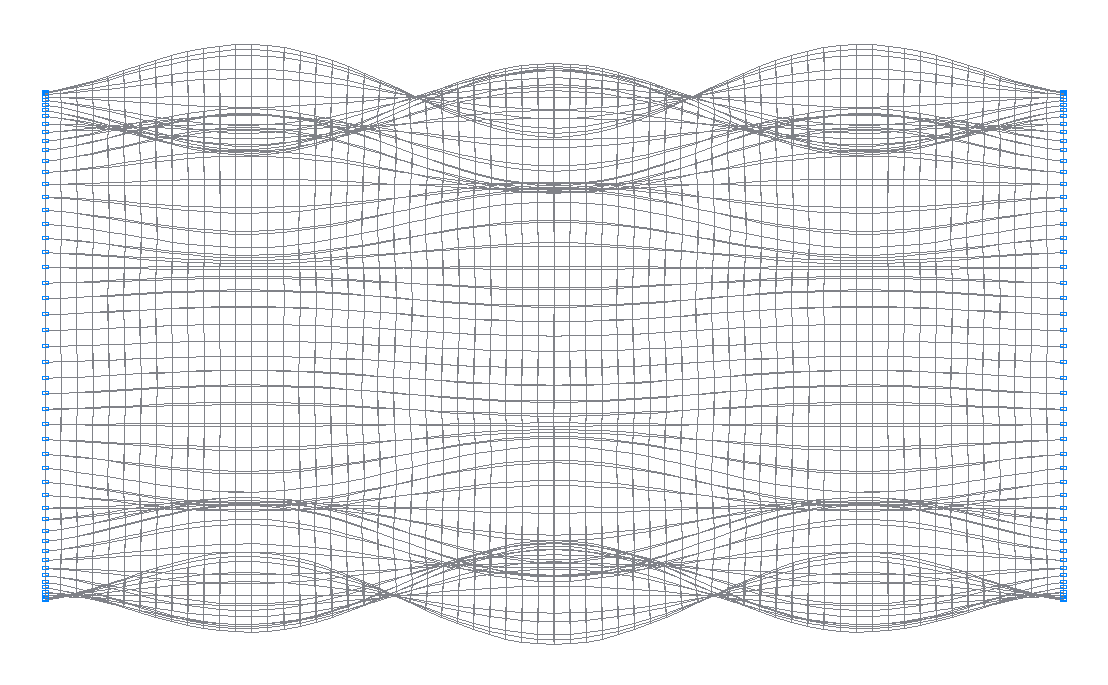
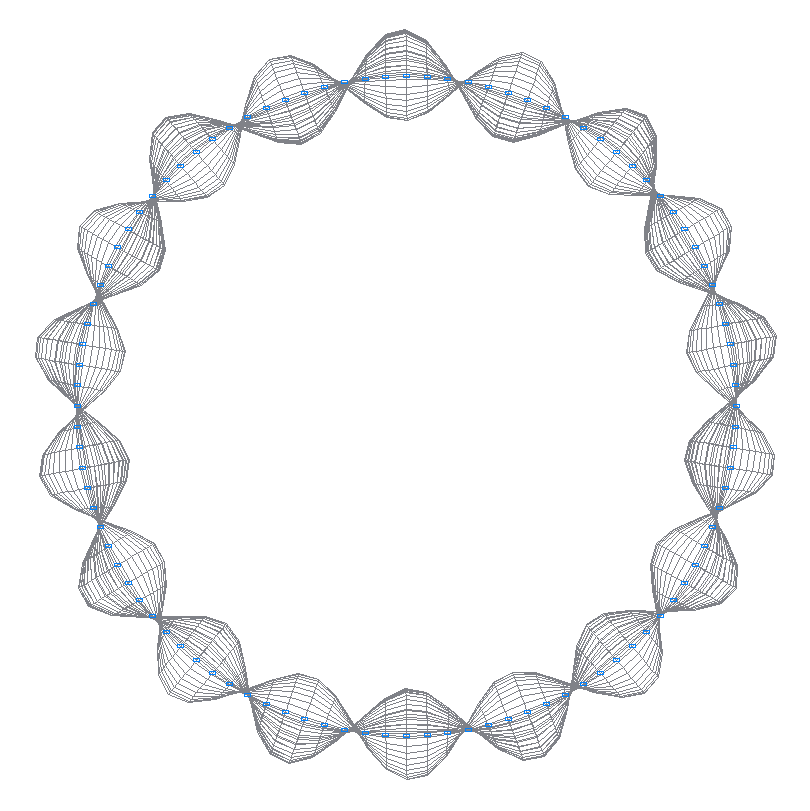
27-я (27-я теоретическая) собственная форма колебаний
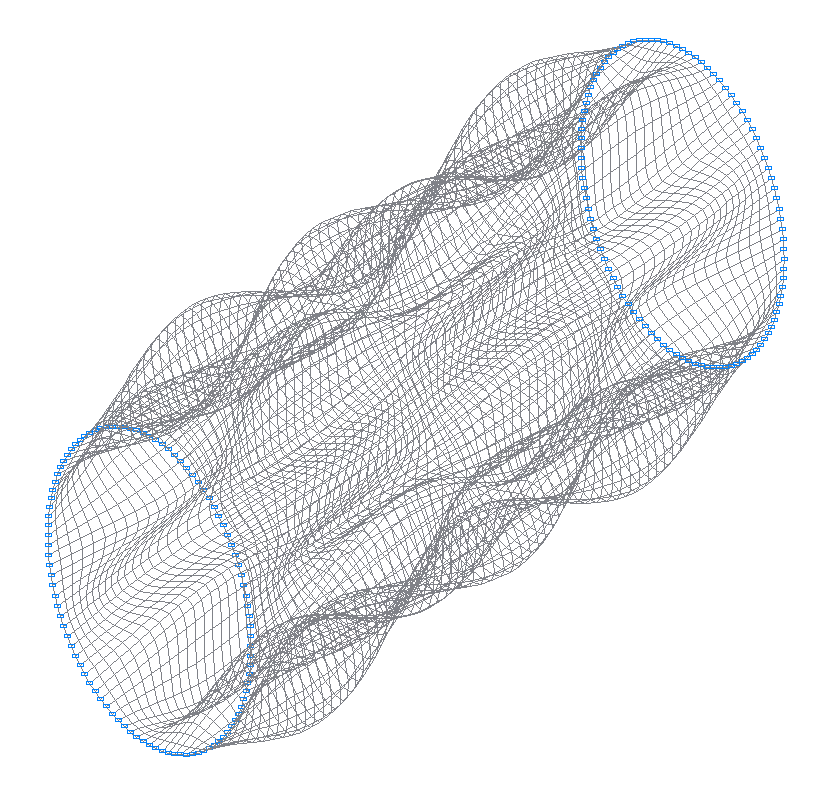
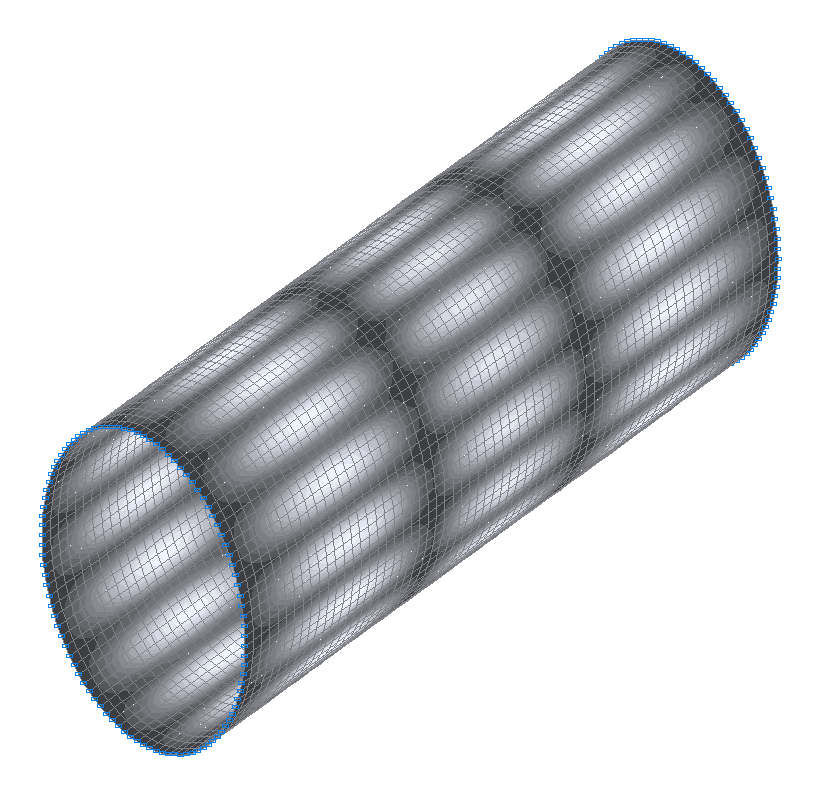
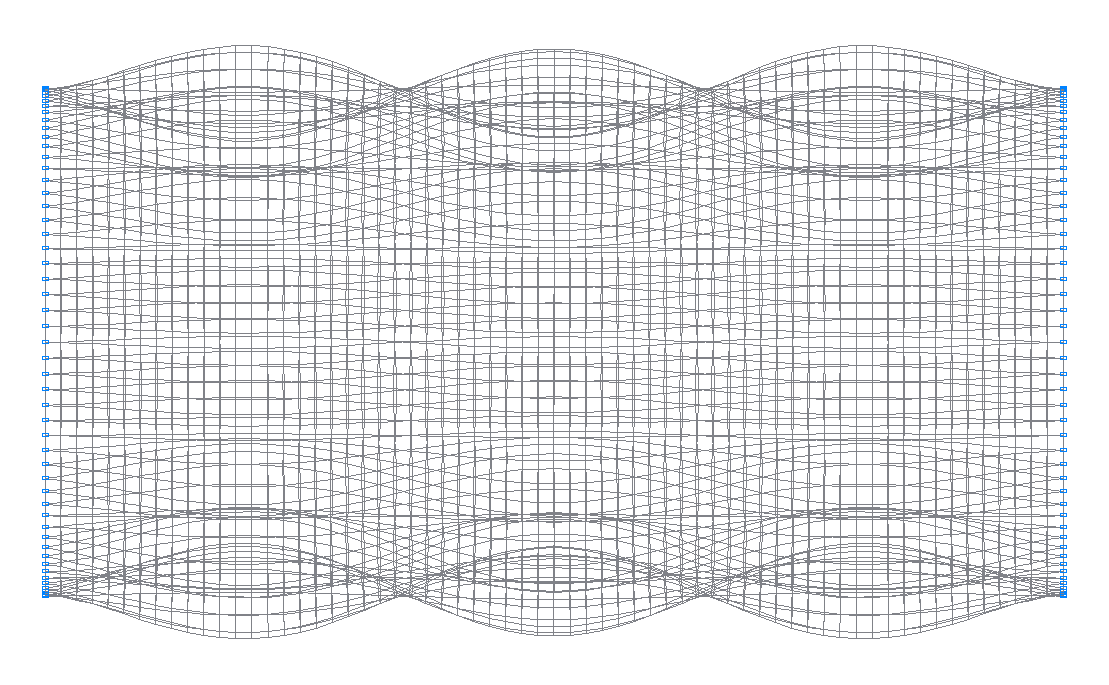
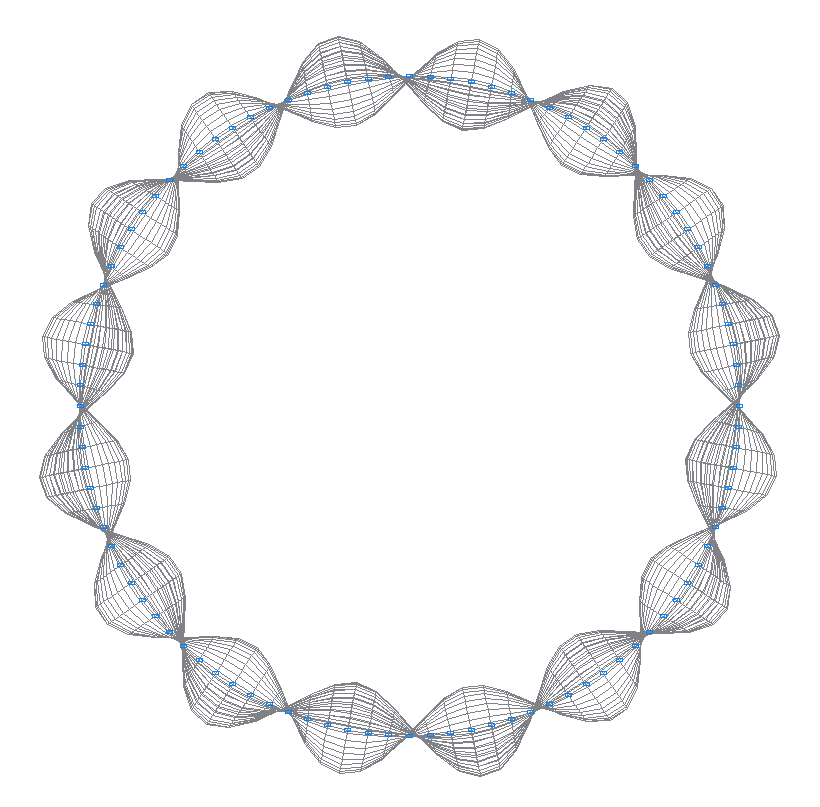
29-я (31-я теоретическая) собственная форма колебаний
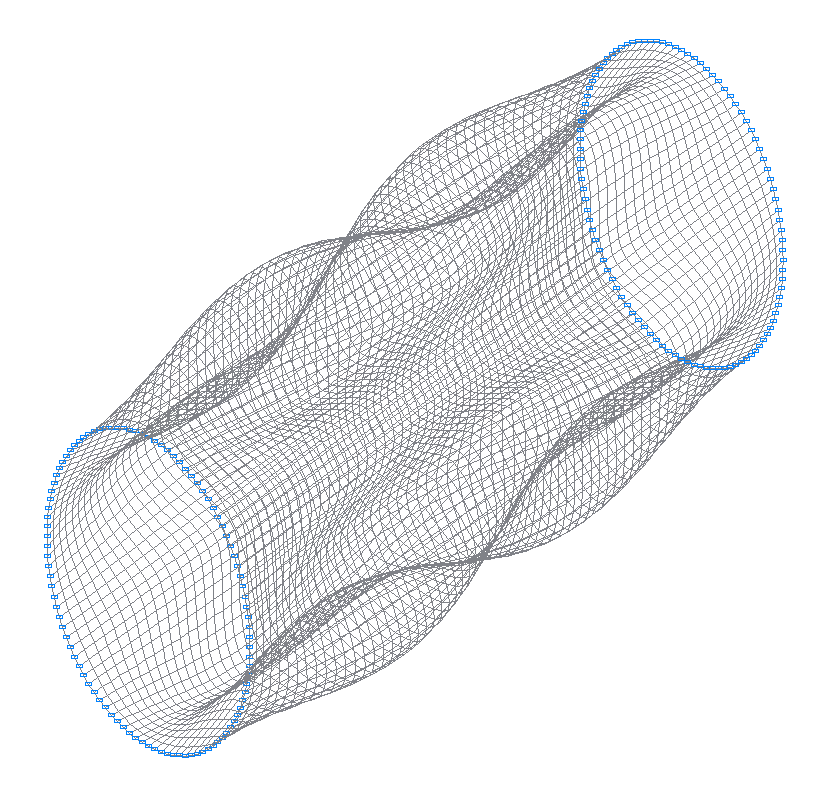
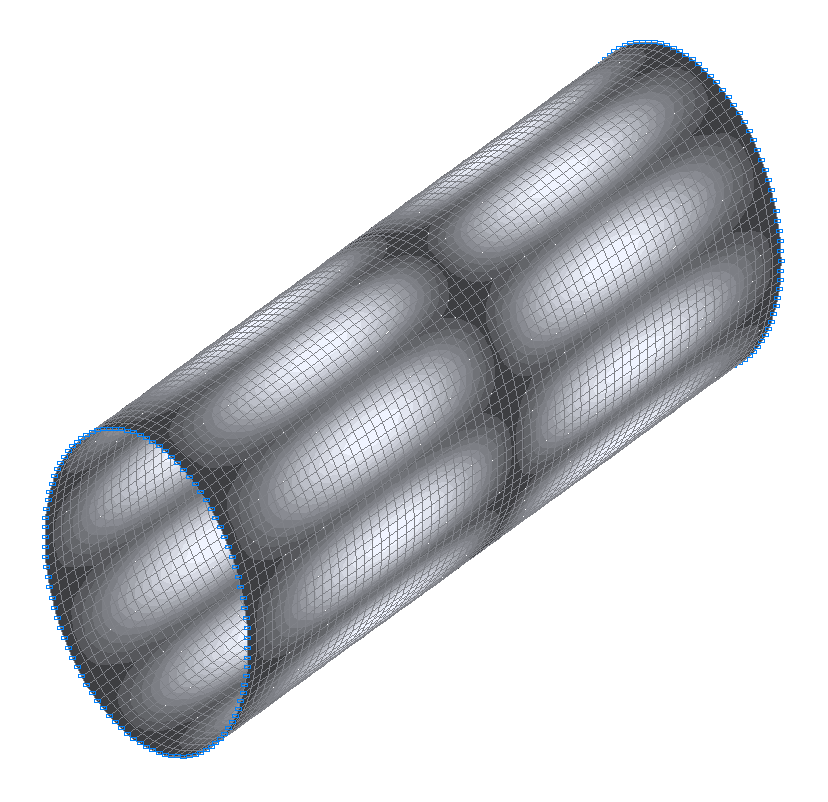
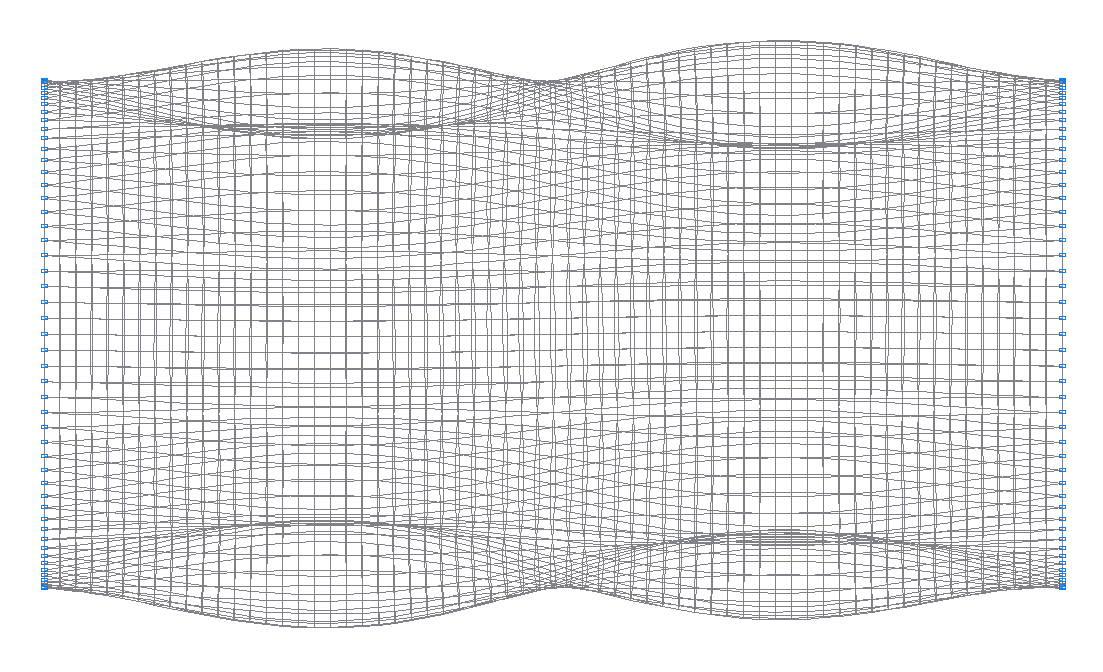
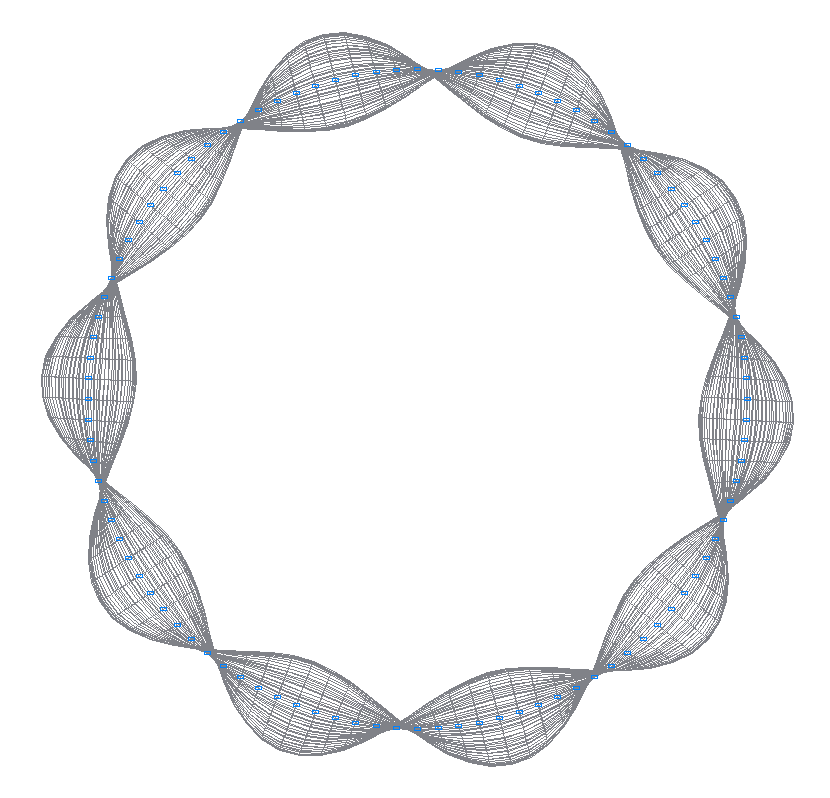
31-я (29-я теоретическая) собственная форма колебаний
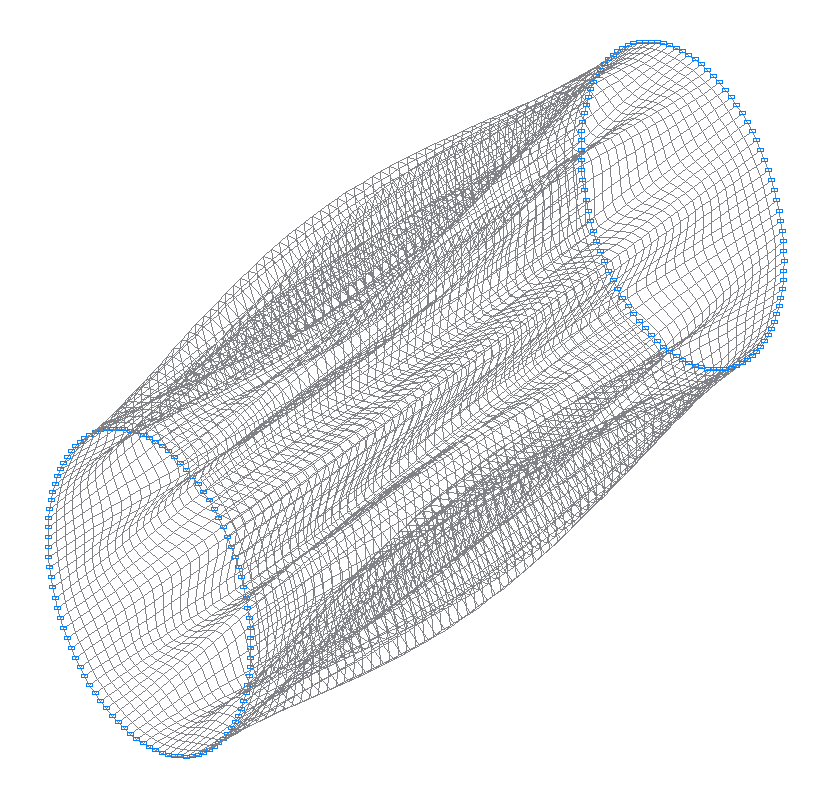

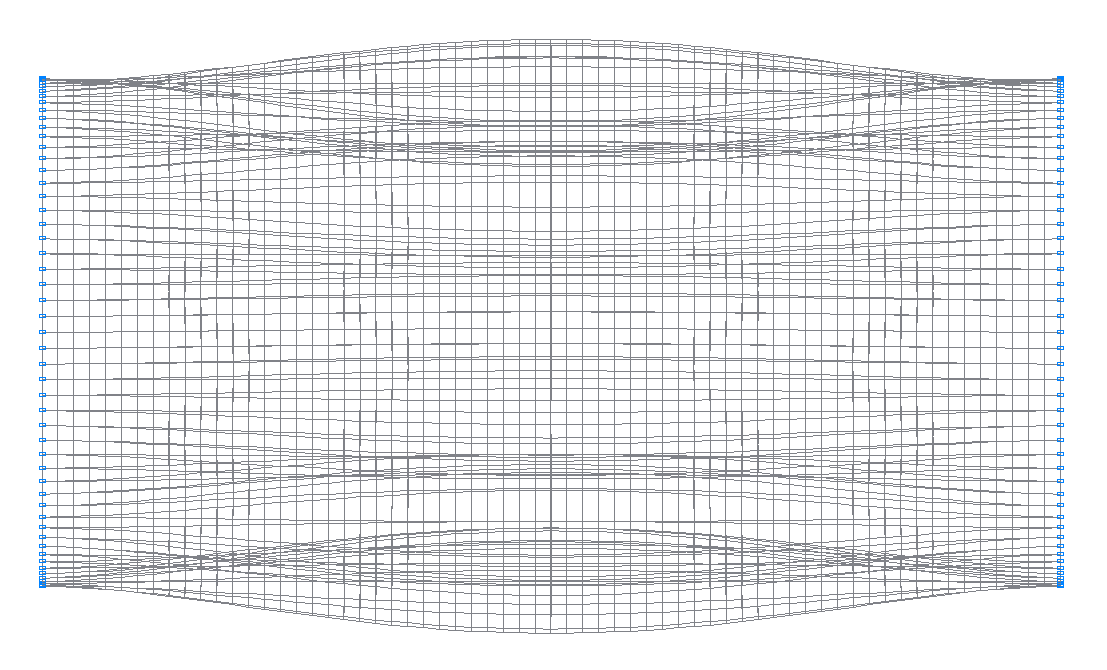
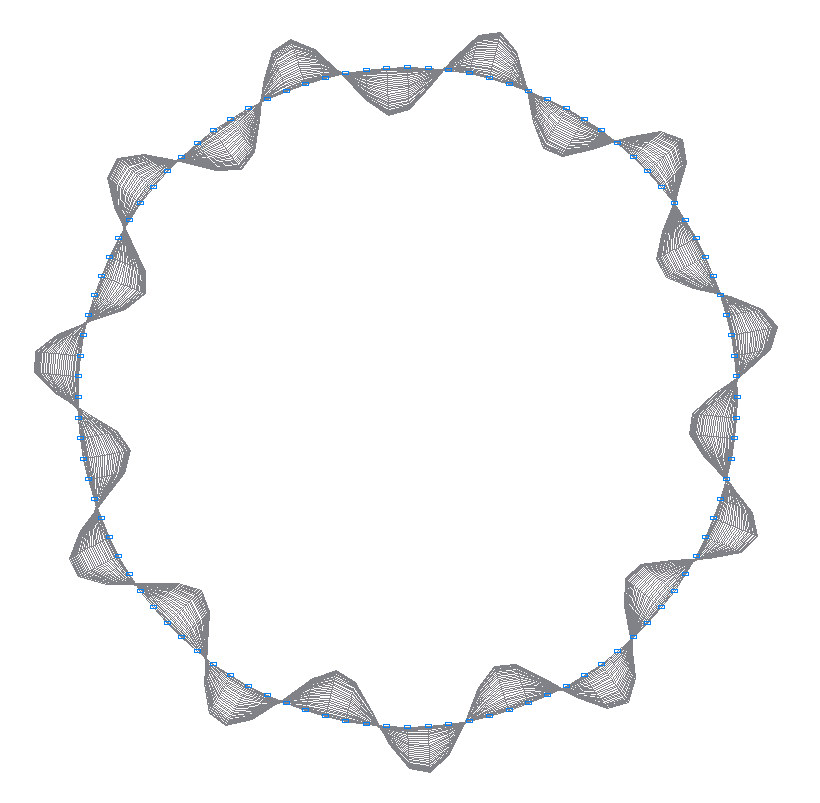
33-я (33-я теоретическая) собственная форма колебаний
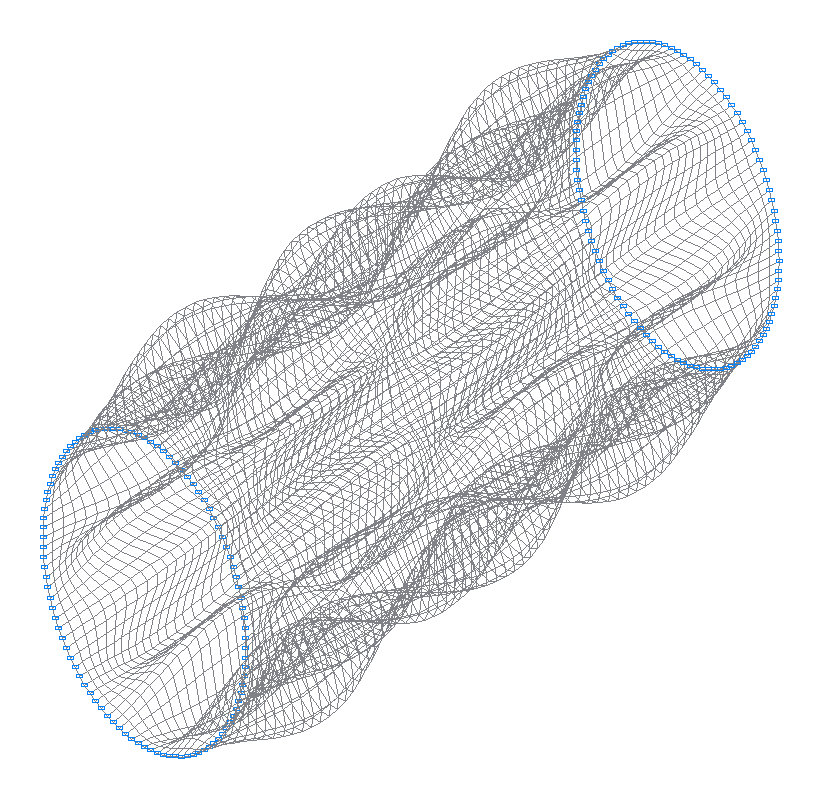
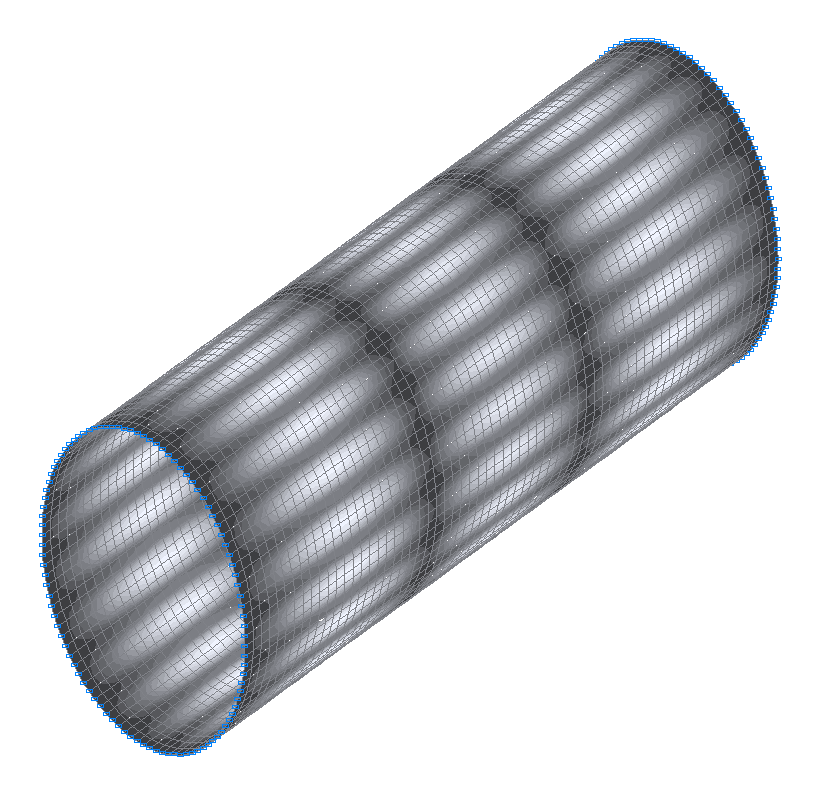
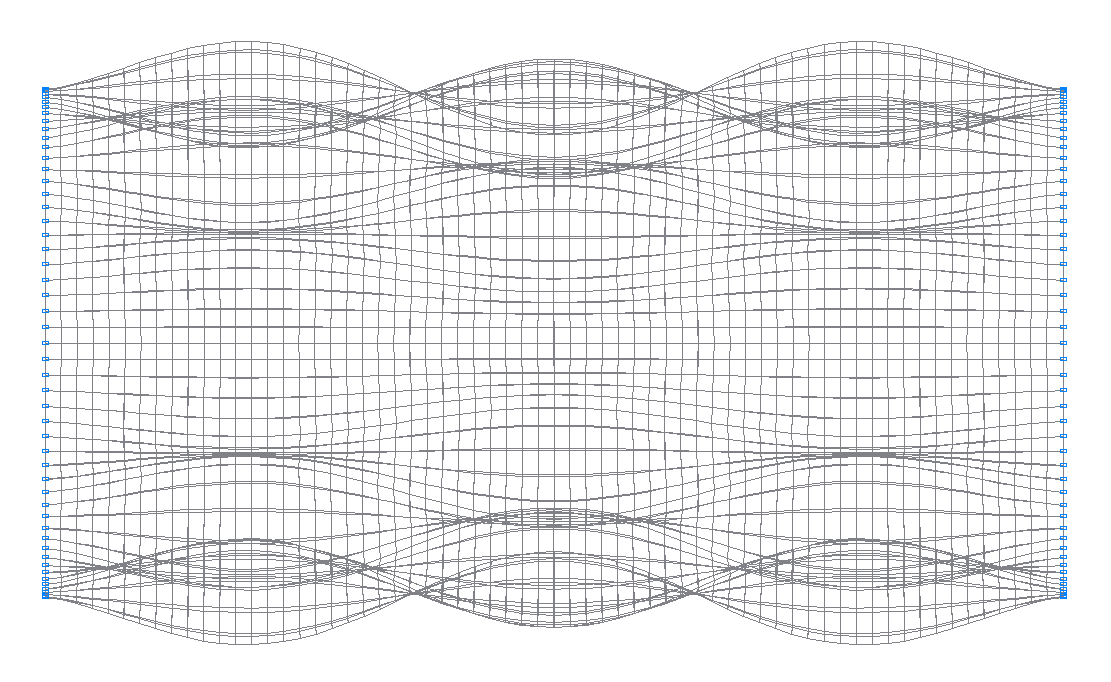
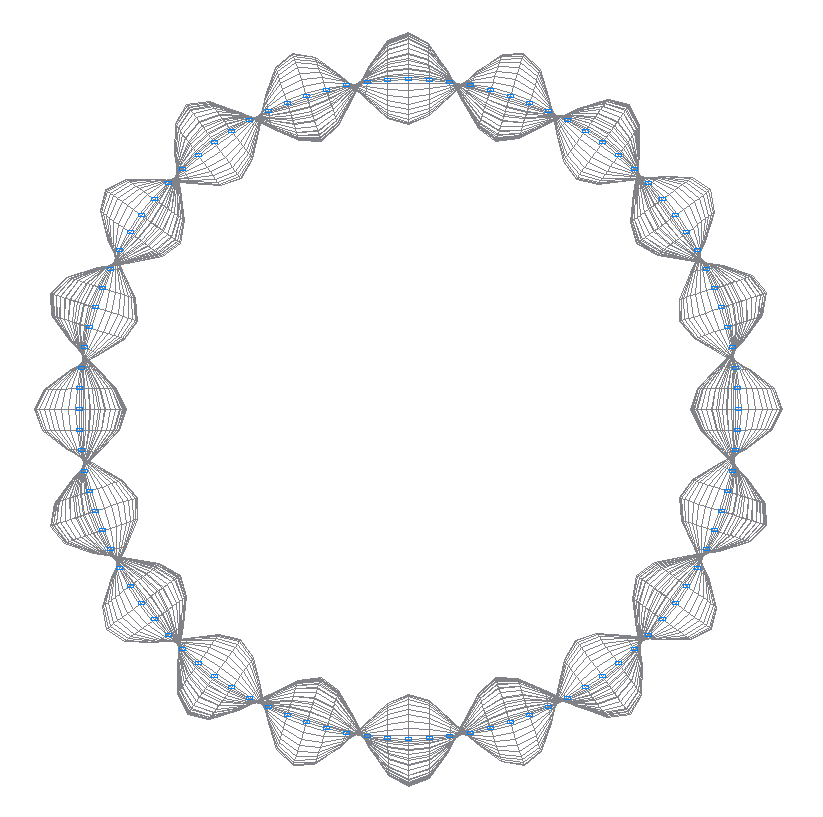
35-я (35-я теоретическая) собственная форма колебаний
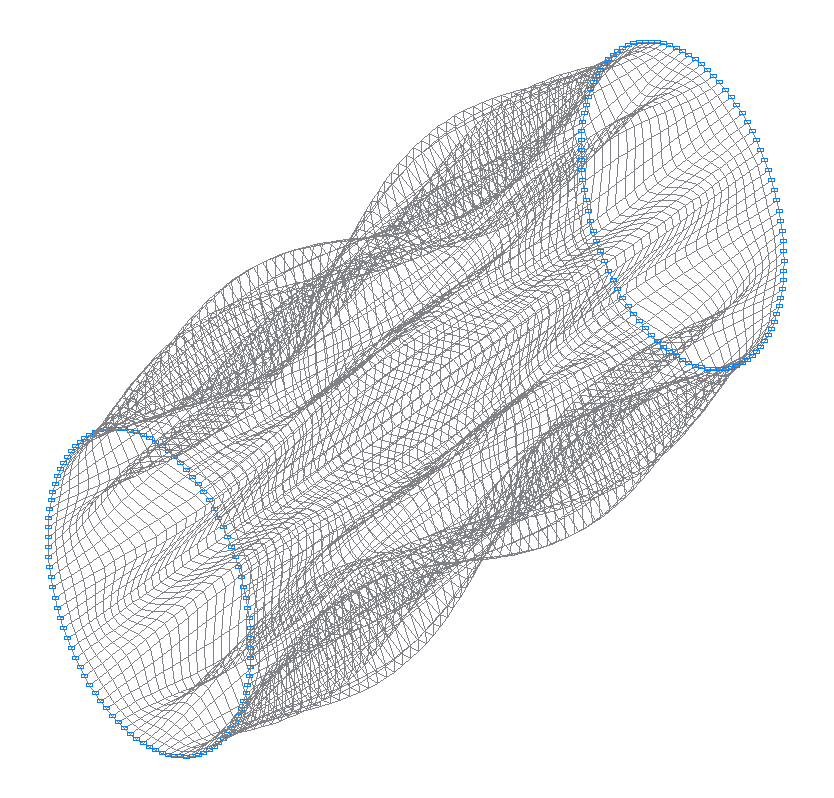
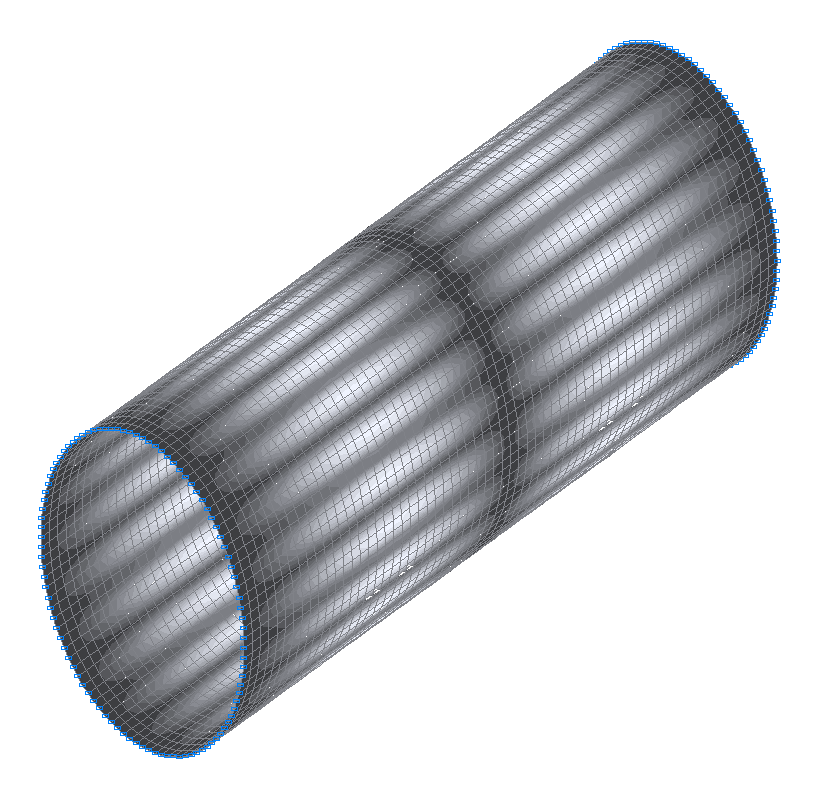


37-я (37-я теоретическая) собственная форма колебаний
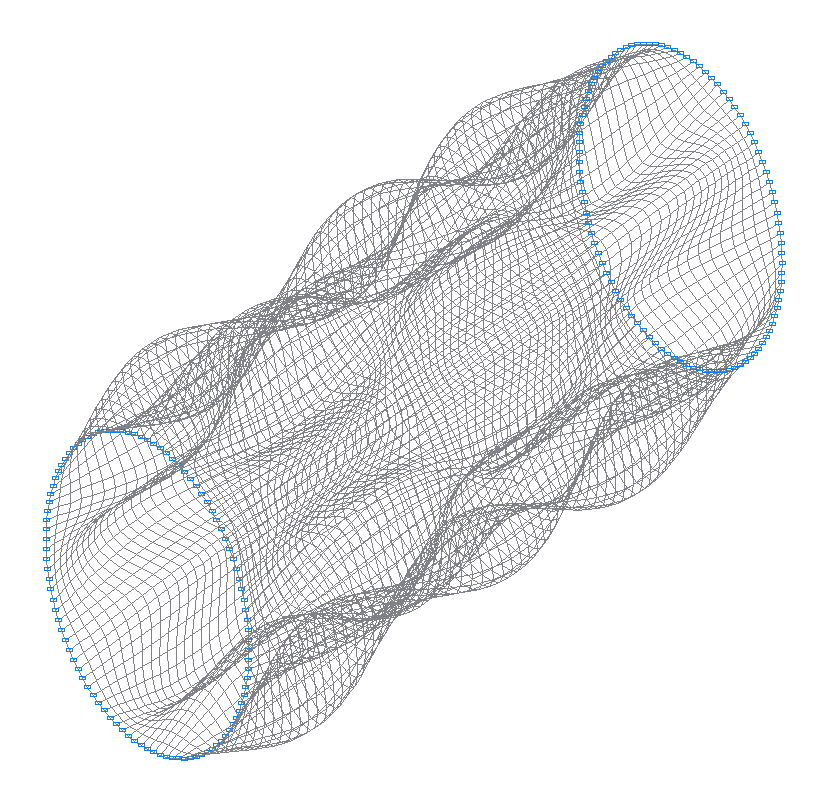
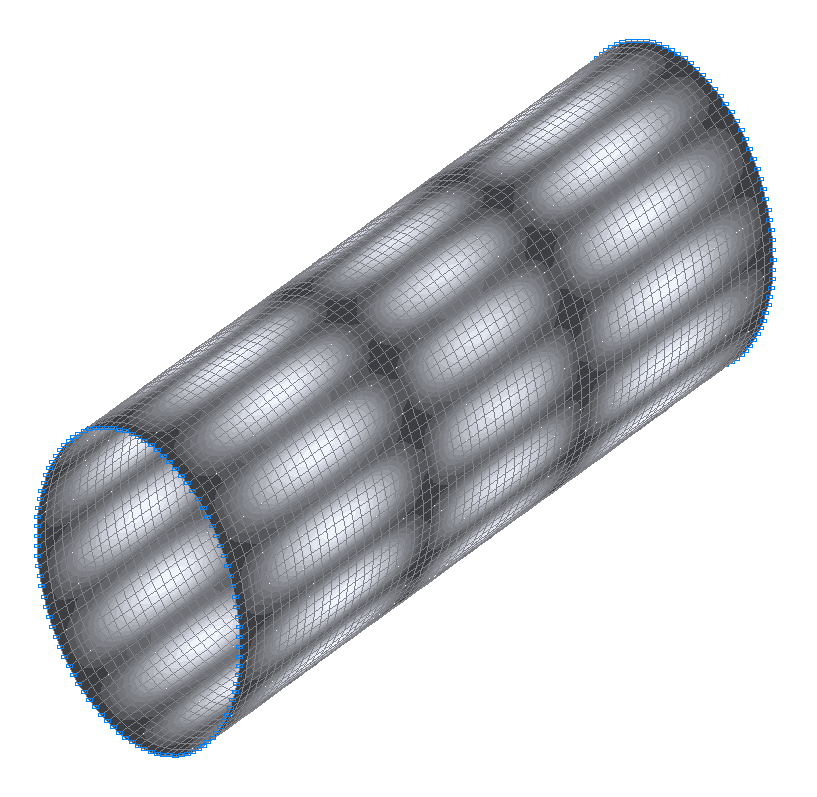
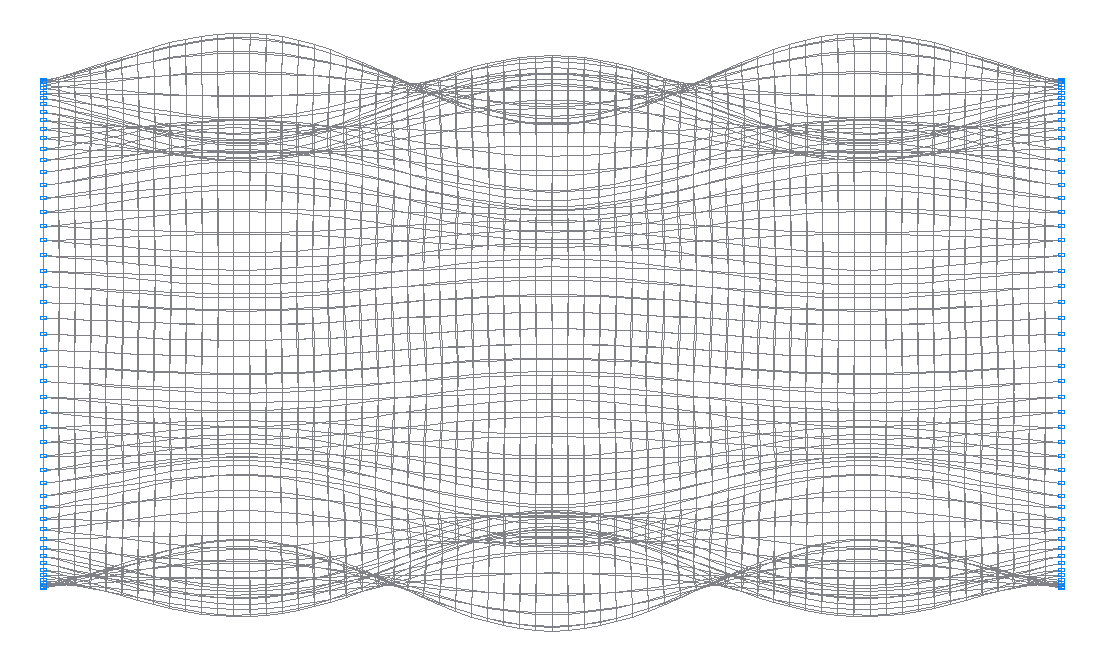
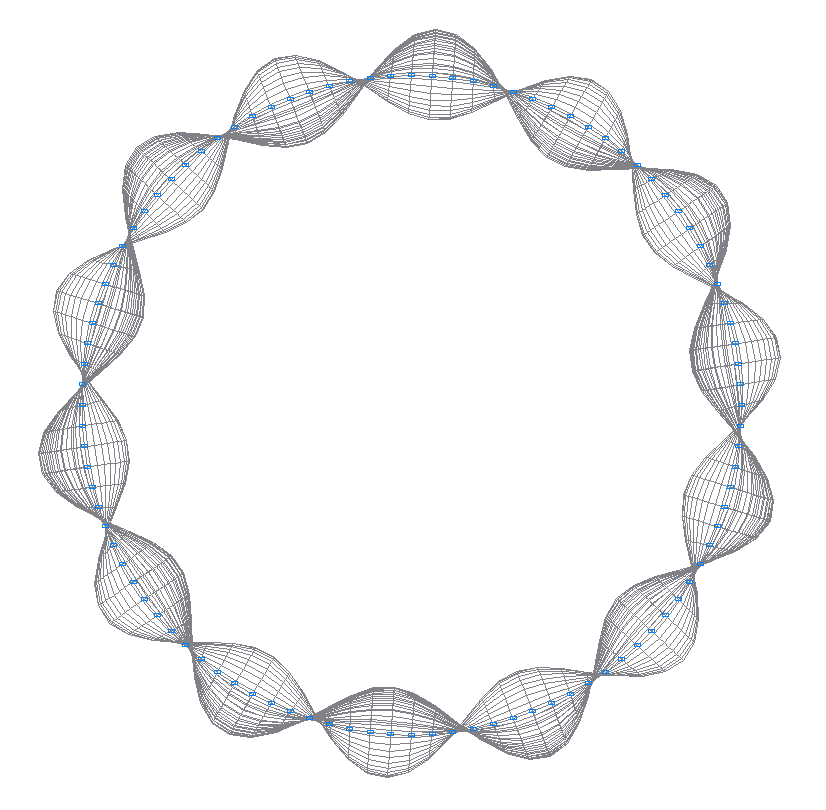
39-я (39-я теоретическая) собственная форма колебаний
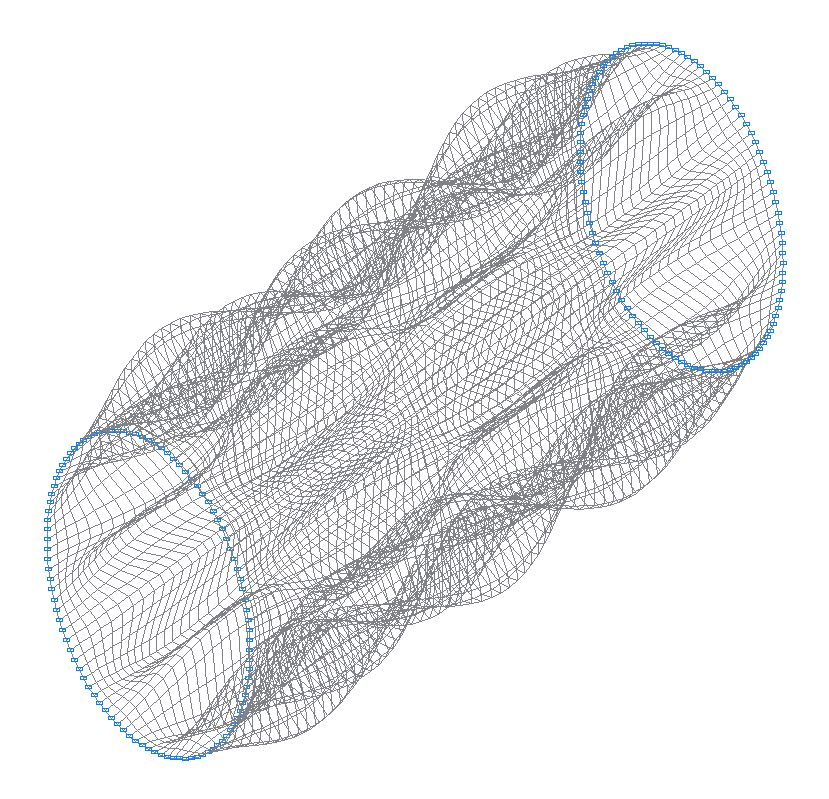
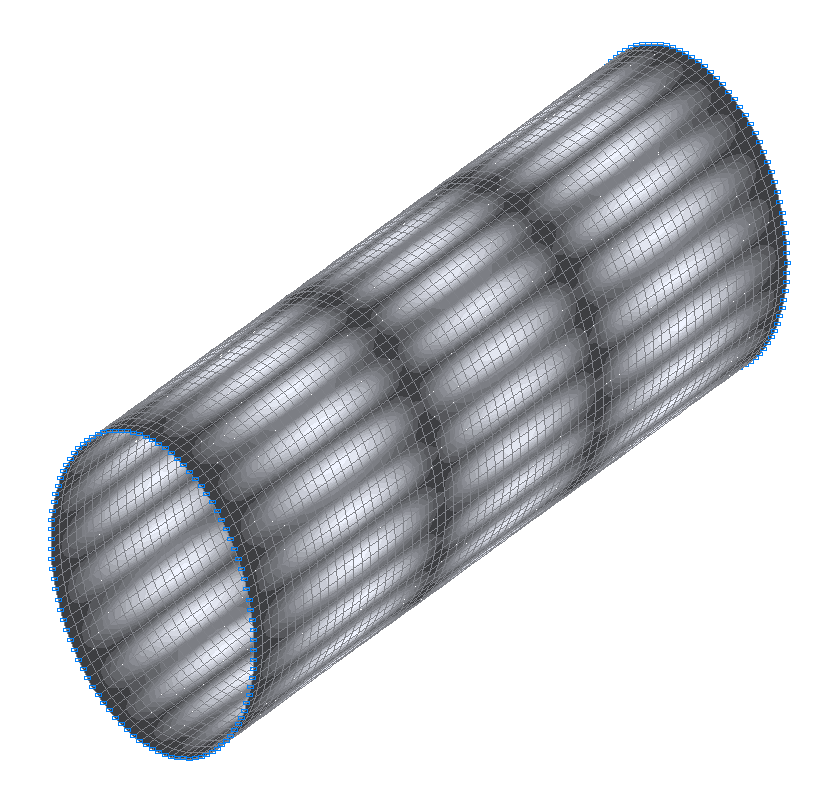
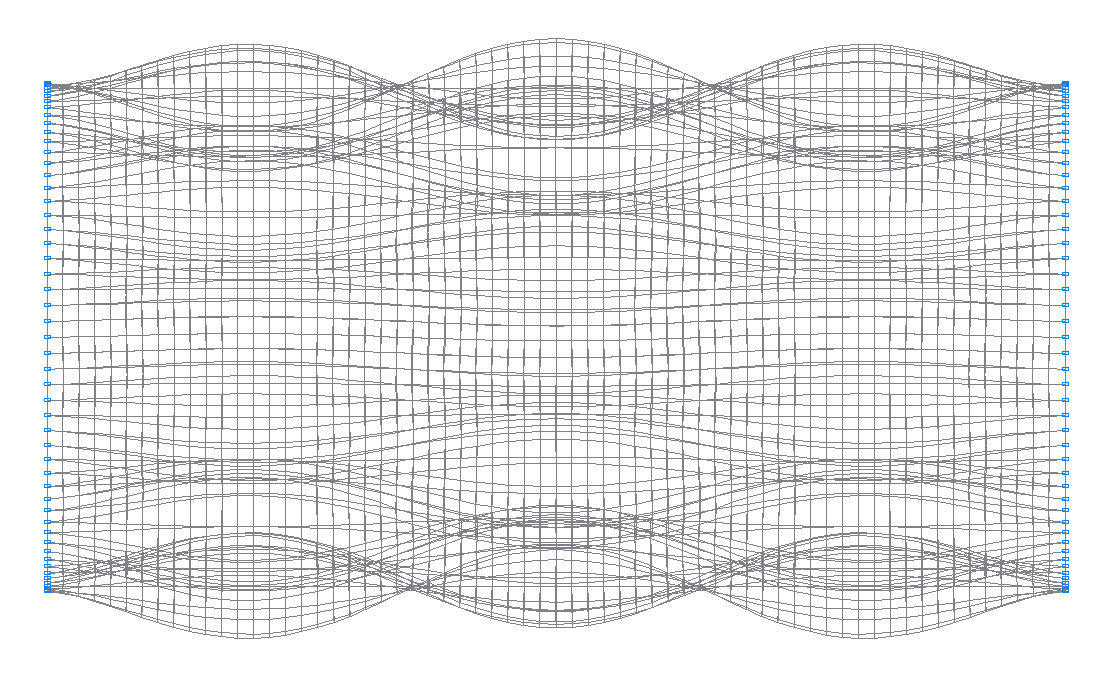
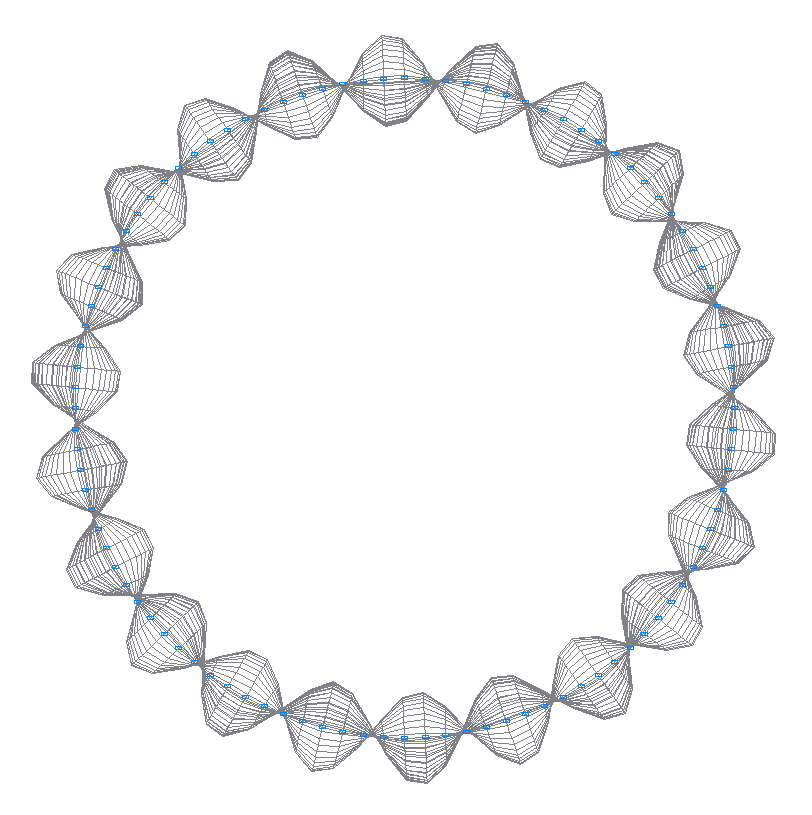
41-я (41-я теоретическая) собственная форма колебаний
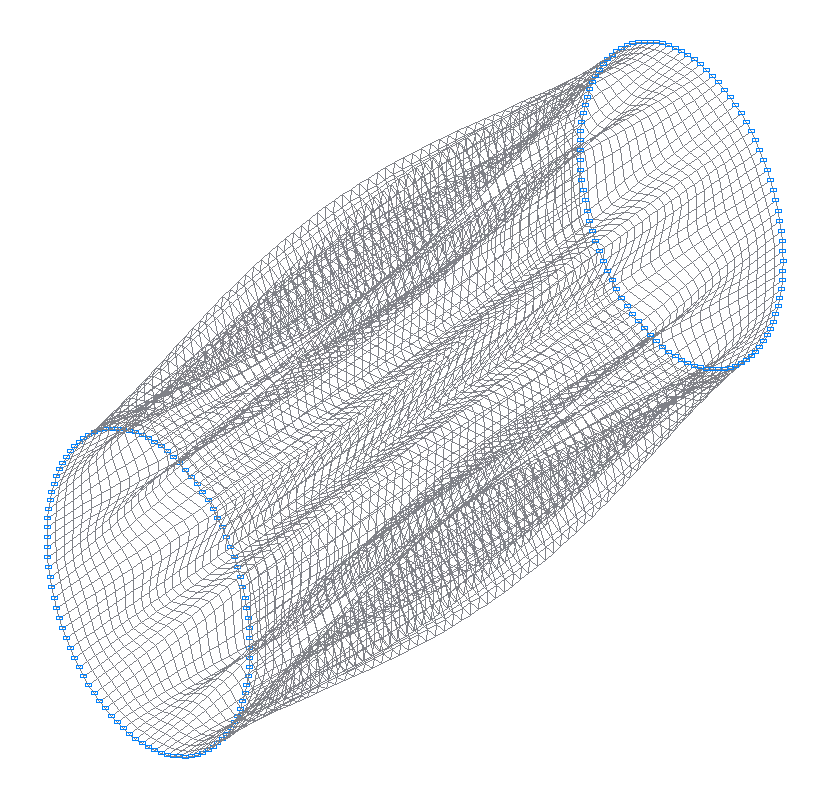

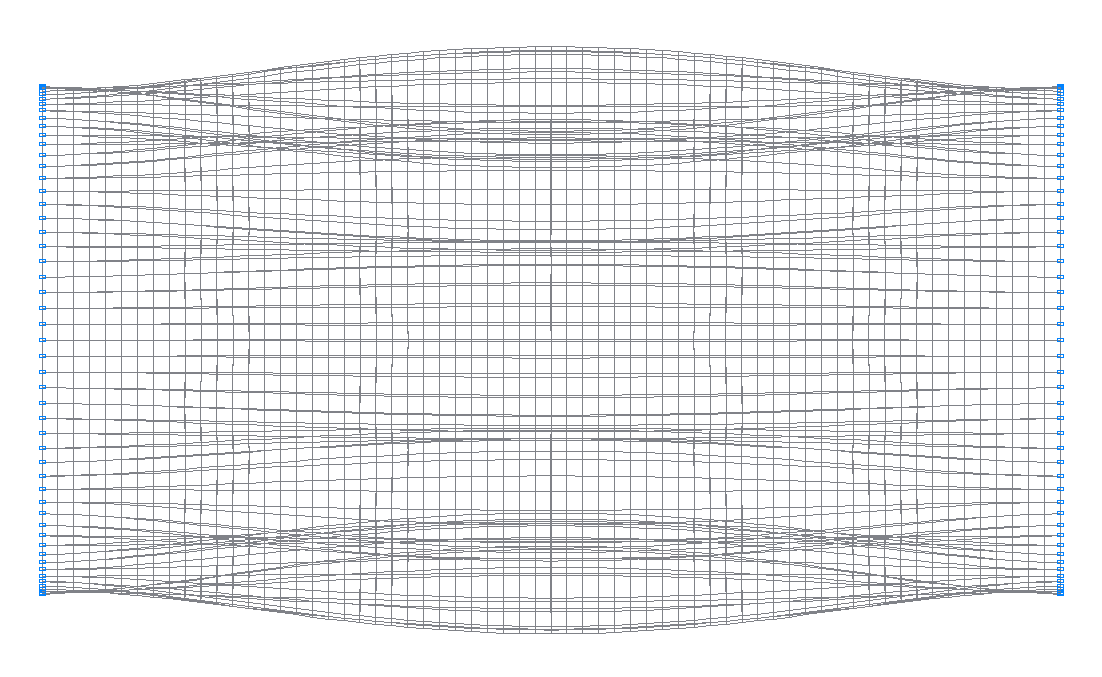
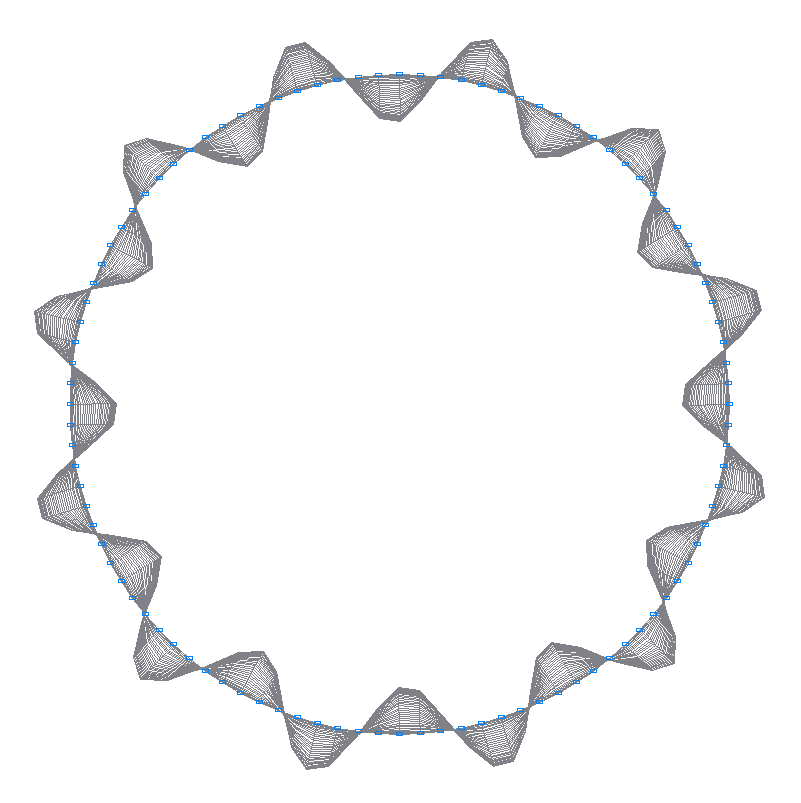
43-я (43-я теоретическая) собственная форма колебаний
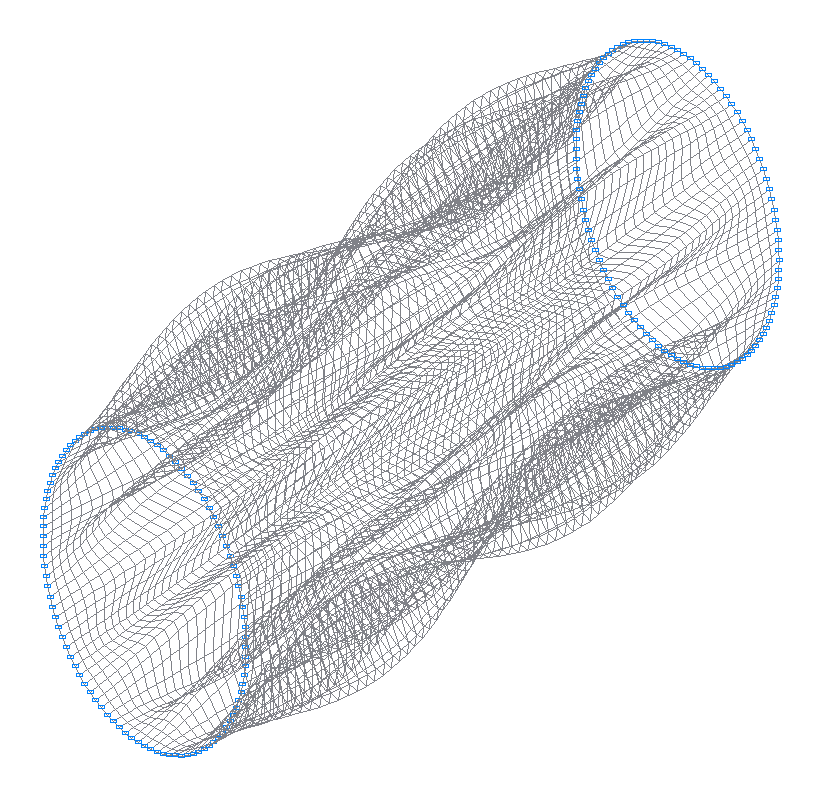
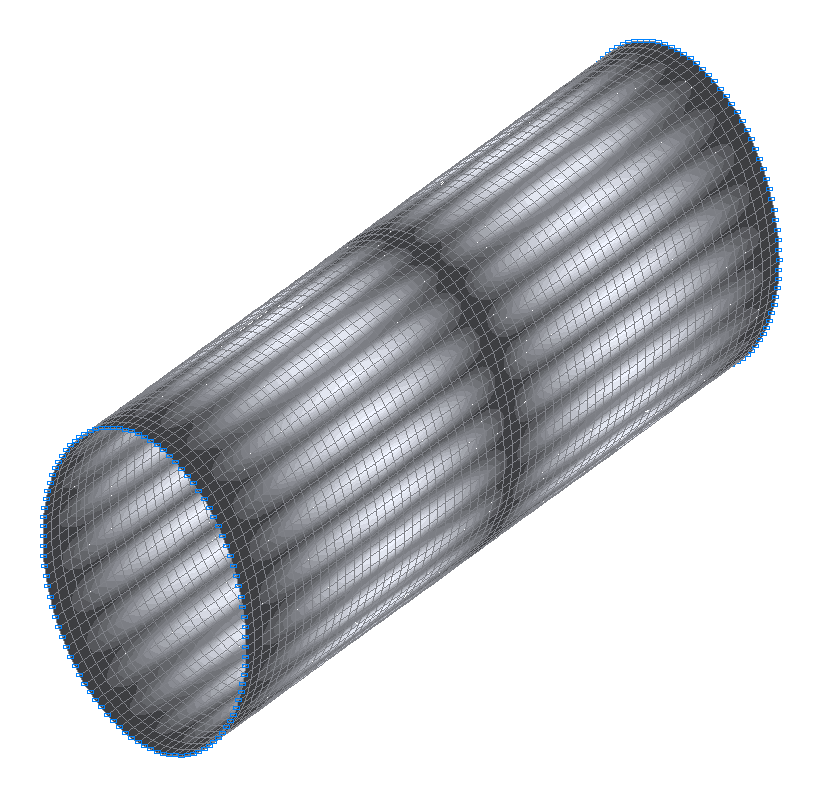


45-я (45-я теоретическая) собственная форма колебаний
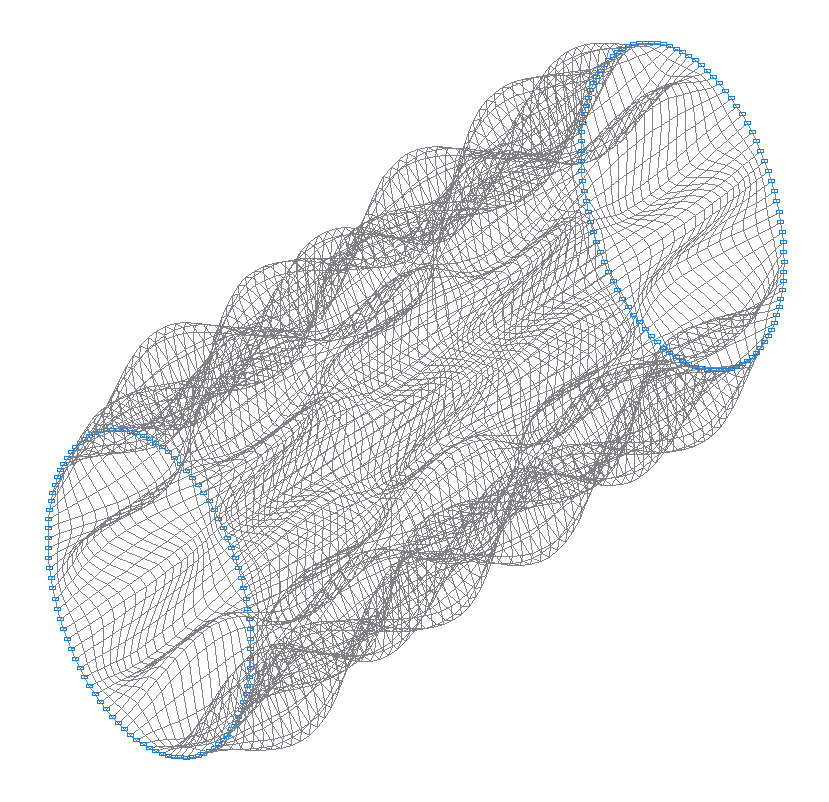
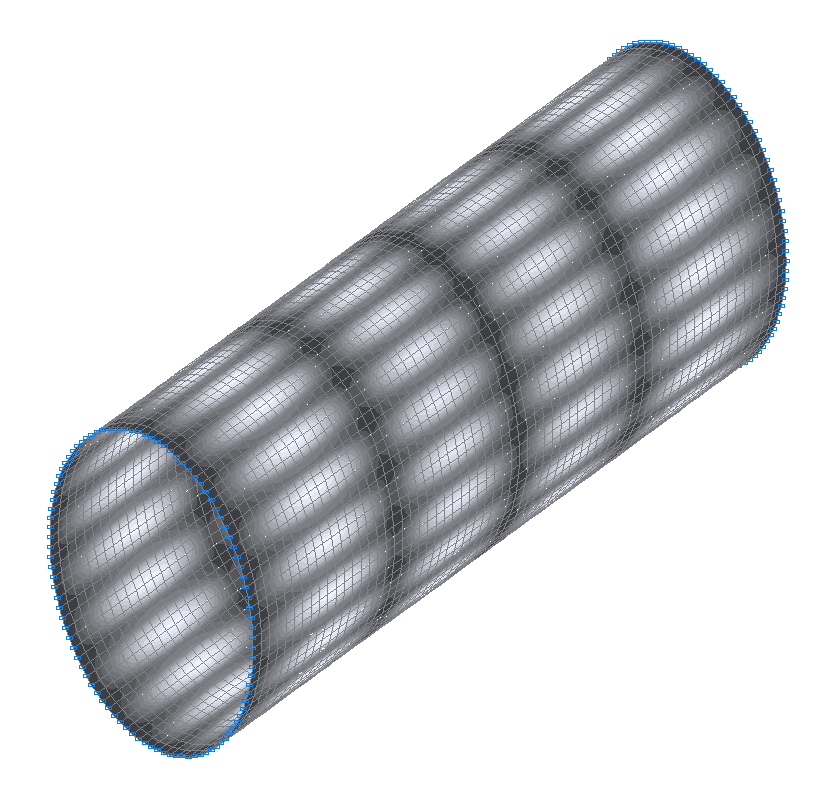
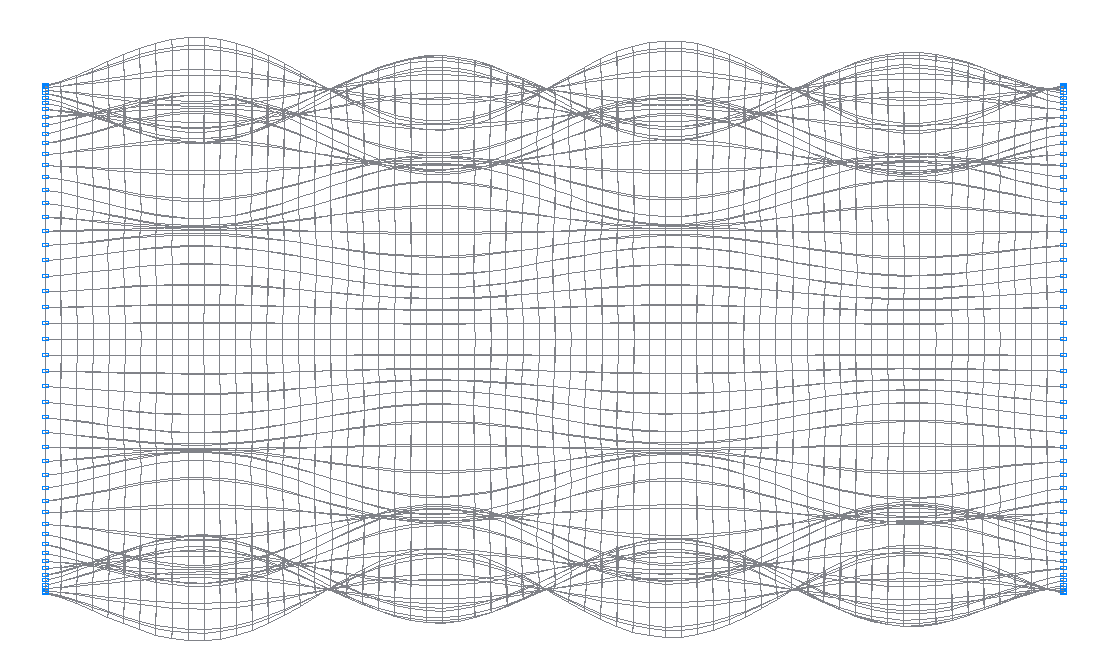

47-я (47-я теоретическая) собственная форма колебаний
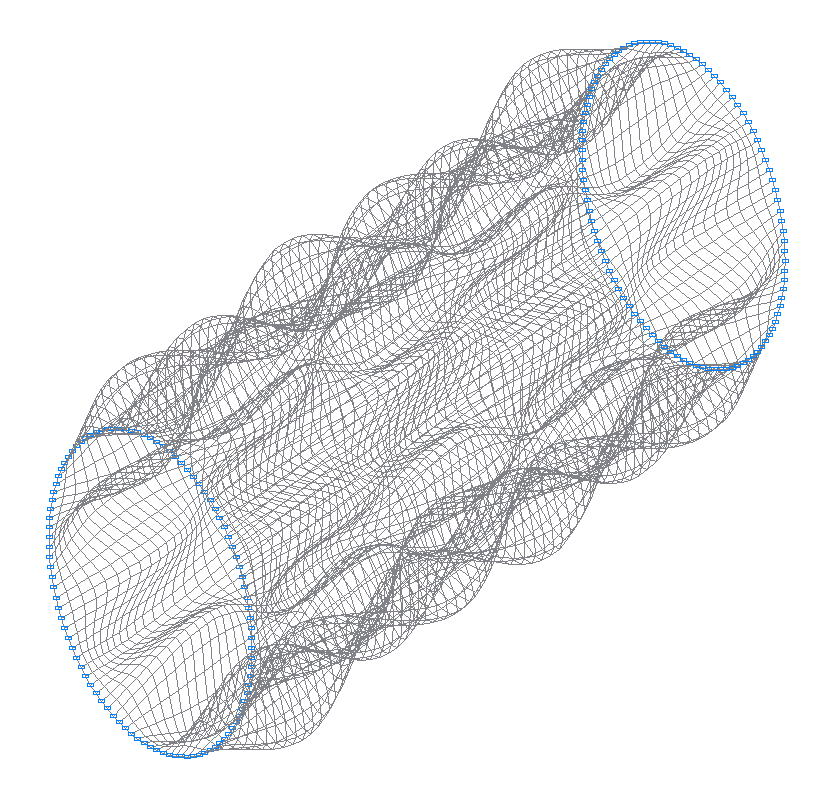
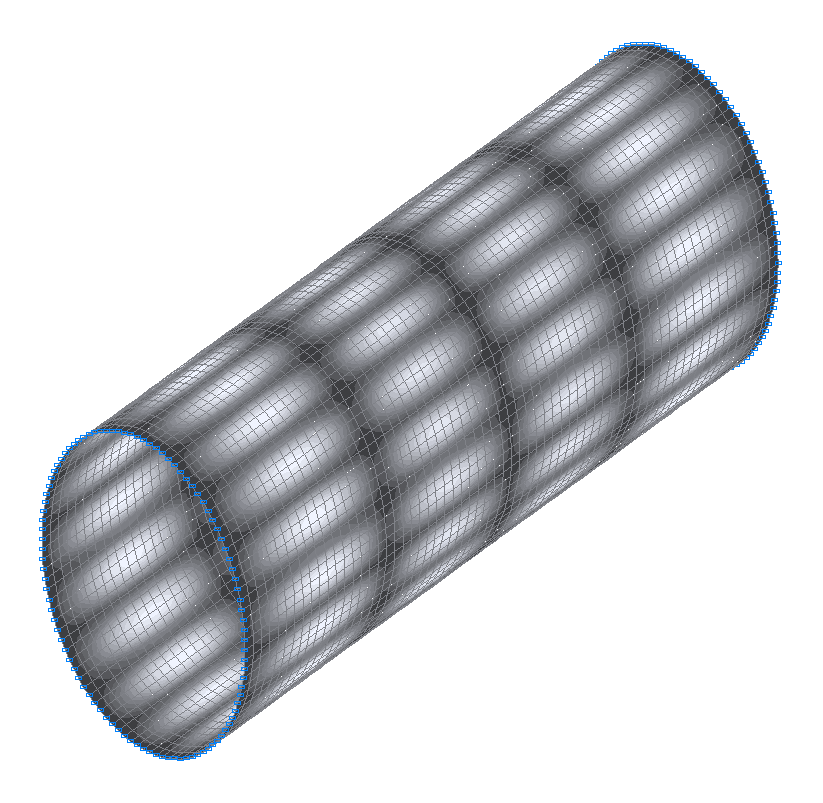
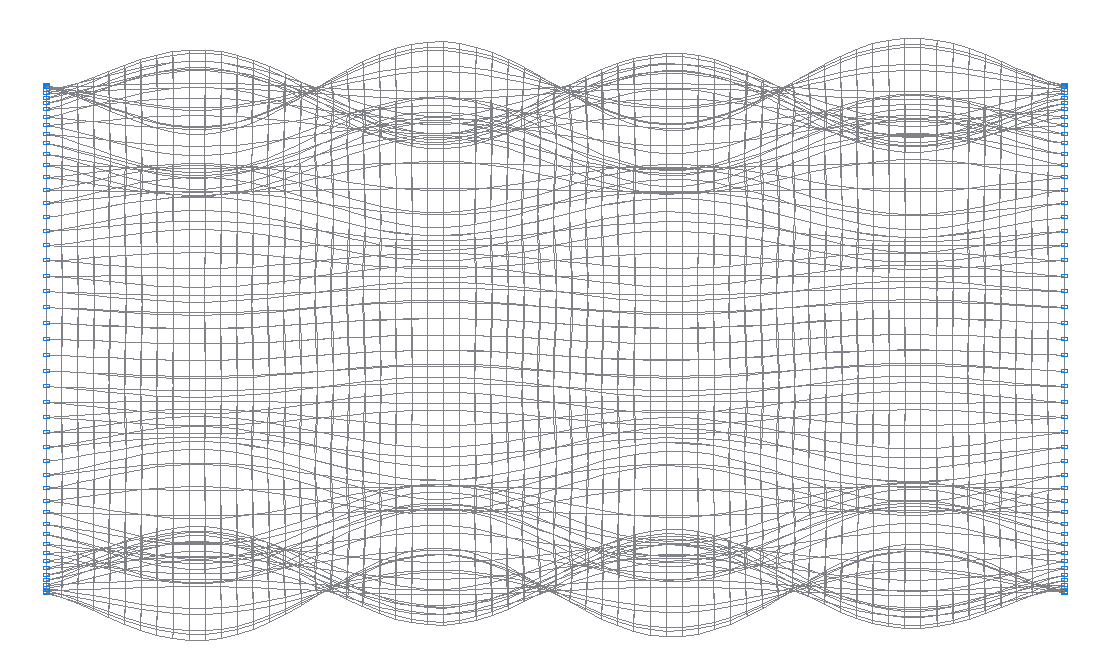
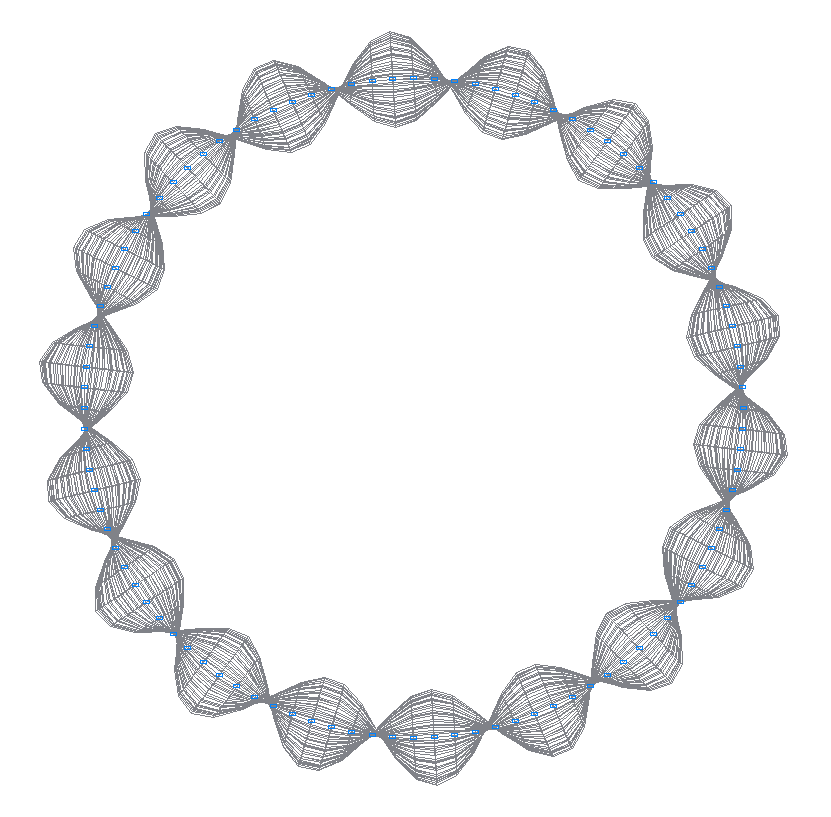
49-я (49-я теоретическая) собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, Гц
|
Форма колебаний |
Число узловых окружностей m и меридианов n |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1, 2 |
2, 6 |
533 (529.2) |
522.2 |
2.03 |
|
3, 4 |
2, 5 |
574 (585.3) |
567.0 |
1.22 |
|
5, 6 |
2, 7 |
593 (579.2) |
578.9 |
2.38 |
|
7, 8 |
2, 8 |
717 (697.2) |
700.3 |
2.33 |
|
9, 10 |
2, 4 |
755 (787.9) |
751.1 |
0.52 |
|
11, 12 |
2, 9 |
881 (857.8) |
862.6 |
2.09 |
|
13, 14 |
3, 7 |
898 (910.0) |
888.2 |
1.09 |
|
15, 16 |
3, 8 |
903 (897.8) |
889.5 |
1.50 |
|
17, 18 |
3, 9 |
996 (979.9) |
979.5 |
1.66 |
|
19, 20 |
3, 6 |
1011 (1047.7) |
1004.6 |
0.63 |
|
21, 22 |
2, 10 |
1075 (1048.9) |
1054.6 |
1.90 |
|
23, 24 |
2, 3 |
1140 (1209.6) |
1136.7 |
0.29 |
|
25, 26 |
3, 10 |
1151 (1127.1) |
1131.1 |
1.73 |
|
27, 28 |
4, 9 |
1251 (1251.3) |
1238.2 |
1.02 |
|
29, 30 |
3, 5 |
1272 (1344.8) |
1267.7 |
0.34 |
|
31, 32 |
4, 8 |
1273 (1293.0) |
1264.2 |
0.69 |
|
33, 34 |
2, 11 |
1295 (1265.4) |
1271.5 |
1.81 |
|
35, 36 |
4, 10 |
1325 (1310.9) |
1308.2 |
1.27 |
|
37, 38 |
3, 11 |
1348 (1319.3) |
1325.7 |
1.65 |
|
39, 40 |
4, 7 |
1415 (1460.8) |
1409.3 |
0.40 |
|
41, 42 |
4, 11 |
1471 (1446.7) |
1450.2 |
1.41 |
|
43, 44 |
2, 12 |
—— (1504.9) |
1511.3 |
- |
|
45, 46 |
3, 12 |
—— (1545.3) |
1552.9 |
- |
|
47, 48 |
5, 10 |
—— (1611.9) |
1597.9 |
- |
|
49, 50 |
5, 9 |
—— (1657.6) |
1627.9 |
- |
|
51, 52 |
3, 12 |
—— (1637.7) |
1644.9 |
- |
|
53, 54 |
5, 11 |
—— (1666.7) |
1663.6 |
- |
|
55, 56 |
4, 6 |
1700 (1781.0) |
1696.6 |
0.20 |
|
57, 58 |
3, 4 |
1731 (1863.8) |
1728.3 |
0.16 |
|
59, 60 |
5, 8 |
—— (1824.3) |
1772.9 |
- |
|
61, 62 |
2, 13 |
—— (1766.4) |
1773.0 |
- |
|
63, 64 |
5, 12 |
—— (1800.5) |
1804.6 |
- |
|
65, 66 |
3, 13 |
—— (1799.0) |
1807.3 |
- |
|
67, 68 |
4, 13 |
—— (1869.9) |
1879.4 |
- |
|
69, 70 |
2, 2 |
—— (2045.1) |
1889.1 |
- |
|
71, 72 |
6, 11 |
—— (1975.1) |
1963.8 |
- |
|
73, 74 |
6, 10 |
—— (2007.8) |
1982.0 |
- |
|
75, 76 |
5, 13 |
—— (1994.2) |
2002.9 |
- |
|
77, 78 |
6, 12 |
—— (2038.4) |
2037.7 |
- |
|
79, 80 |
5, 7 |
—— (2131.6) |
2051.4 |
- |
|
81, 82 |
2, 14 |
—— (2049.6) |
2056.1 |
- |
|
83, 84 |
3, 14 |
—— (2077.5) |
2086.0 |
- |
|
85, 86 |
6, 9 |
—— (2154.2) |
2109.1 |
- |
|
87, 88 |
4, 14 |
—— (2135.1) |
2145.7 |
- |
|
89, 90 |
4, 5 |
2165 (2295.4) |
2163.0 |
0.09 |
|
91, 92 |
6, 13 |
—— (2179.6) |
2186.2 |
- |
|
93, 94 |
5, 14 |
—— (2233.9) |
2245.5 |
- |
|
95, 96 |
7, 11 |
—— (2352.7) |
2334.1 |
- |
|
97, 98 |
7, 12 |
—— (2343.7) |
2338.1 |
- |
|
99, 100 |
6, 8 |
—— (2429.8) |
2360.2 |
- |
|
101, 102 |
2, 15 |
—— (2354.1) |
2360.4 |
- |
|
103, 104 |
3, 15 |
—— (2379.1) |
2387.6 |
- |
|
105, 106 |
6, 14 |
—— (2381.8) |
2393.2 |
- |
|
107, 108 |
7, 13 |
—— (2425.1) |
2429.2 |
- |
|
109, 110 |
7, 10 |
—— (2467.4) |
2432.1 |
- |
|
111, 112 |
4, 15 |
—— (2428.2) |
2439.5 |
- |
|
113, 114 |
5, 6 |
—— (2606.7) |
2488.7 |
- |
|
115, 116 |
3, 3 |
2505 (2740.1) |
2502.6 |
0.10 |
|
117, 118 |
5, 15 |
—— (2510.3) |
2523.6 |
- |
|
119, 120 |
7, 14 |
—— (2581.1) |
2592.0 |
- |
|
121, 122 |
7, 14 |
—— (2700.8) |
2644.8 |
- |
|
123, 124 |
7, 9 |
—— (2632.0) |
2646.5 |
- |
|
125, 126 |
6, 15 |
—— (2679.8) |
2685.7 |
- |
|
127, 128 |
2, 16 |
—— (2701.6) |
2692.7 |
- |
|
129,130 |
8, 12 |
—— (2702.9) |
2711.1 |
- |
|
131, 132 |
3, 16 |
—— (2723.2) |
2725.6 |
- |
|
133, 134 |
8, 13 |
—— (2852.2) |
2752.7 |
- |
|
135, 136 |
6, 7 |
—— (2777.7) |
2754.5 |
- |
|
137, 138 |
8, 11 |
—— (2746.6) |
2757.9 |
- |
|
139, 140 |
4, 16 |
—— (2796.9) |
2812.5 |
- |
|
141, 142 |
5, 16 |
—— (2817.6) |
2831.6 |
- |
|
143, 144 |
7, 15 |
—— (2829.0) |
2839.8 |
- |
|
145, 146 |
4, 4 |
2884 (3082.7) |
2883.1 |
0.03 |
|
147, 148 |
8, 10 |
—— (2963.2) |
2922.5 |
- |
|
149, 150 |
6, 16 |
—— (2921.1) |
2937.5 |
- |
В графе «Теория» перед скобками указаны значения точного решения, а в скобках – значения приближенного решения по методу Рэлея-Ритца с выражением компонент перемещений с помощью балочных функций.
Замечания: При аналитическом решении по методу Рэлея-Ритца с выражением компонент перемещений с помощью балочных функций собственные частоты колебаний ω круговой цилиндрической оболочки, защемленной по торцам, с плотностью материала ρ определяются из характеристического уравнения:
\[\left( {\frac{4\cdot \pi^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)^{3}\cdot \omega^{6}+K2\cdot \left( {\frac{4\cdot \pi ^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)^{2}\cdot \omega^{4}+K1\cdot \left( {\frac{4\cdot \pi^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)\cdot \omega ^{2}+K0=0, \quad где: \] \[ {\begin{array}{*{20}c} {K2=-1-\frac{1}{2}\cdot \left[ {\left( {\frac{2}{\delta_{m} }+\delta_{m} -\nu \cdot \delta_{m} } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}+\left( {3-\nu } \right)\cdot n^{2}} \right]-} \\ {\frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\left[ {\left( {\frac{\lambda _{m} \cdot R}{L}} \right)^{4}+2\cdot \delta_{m} \cdot \left( {\frac{\lambda _{m} \cdot R}{L}} \right)^{2}\cdot n^{2}+n^{4}} \right]+2\cdot \left( {1-\nu } \right)\cdot \delta_{m} \cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}+n^{2}} \right\}} \\ \end{array} } \] \[ {\begin{array}{*{20}c} {K1=\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \left[ {\left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}+2\cdot \left( {\frac{1-\nu \cdot \delta_{m}^{2}}{\left( {1-\nu } \right)\cdot \delta_{m} }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}\cdot n^{2}+n^{4}} \right]+} \\ {\frac{1}{2}\cdot \left( {\frac{2}{\delta_{m} }+\delta_{m} -\nu \cdot \delta_{m} -2\cdot \nu^{2}\cdot \delta_{m} } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}+\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot n^{2}+} \\ {\frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\frac{1}{2}\cdot \left[ {\left( {\frac{2}{\delta_{m} }+\delta_{m} -\nu \cdot \delta_{m} } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{6}+\left( {7+2\cdot \delta _{m}^{2}-\left( {1+2\cdot \delta_{m}^{2}} \right)\cdot \nu } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}\cdot n^{2}+} \right.} \right.} \\ {\left. {\left( {\frac{2}{\delta_{m} }+7\cdot \delta_{m} -3\cdot \nu \cdot \delta_{m} } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}\cdot n^{4}+\left( {3-\nu } \right)\cdot n^{6}} \right]+2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}-} \\ {\left. {\left( {3\cdot \delta_{m} -\frac{1}{\delta_{m} }-\nu^{2}\cdot \delta_{m} } \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}\cdot n^{2}-\frac{1}{2}\cdot \left( {3+\nu } \right)\cdot n^{4}+2\cdot \left( {1-\nu } \right)\cdot \delta_{m} \cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}+n^{2}} \right\} } \\ \end{array} } \] \[ {\begin{array}{*{20}c} {K0=-\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \left( {1-\nu^{2}\cdot \delta_{m}^{2}} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}-\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\left[ {\left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{8}+2\cdot \left( {\frac{1+\delta_{m}^{2}-2\cdot \nu \cdot \delta_{m} }{\left( {1-\nu } \right)\cdot \delta_{m} }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{6}\cdot n^{2}} \right.+} \right.} \\ {\left. {\left( {\frac{6-2\cdot \nu \cdot \left( {1+2\cdot \delta_{m} ^{2}} \right)}{1-\nu }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}\cdot n^{4}+2\cdot \left( {\frac{1+\delta_{m}^{2}-2\cdot \nu \cdot \delta_{m} }{\left( {1-\nu } \right)\cdot \delta_{m} }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}\cdot n^{6}+n^{8}} \right]-} \\ {2\cdot \left( {\frac{4-2\cdot \nu \cdot \left( {1+\delta_{m}^{2}} \right)-\nu^{2}\cdot \delta_{m}^{2}\cdot \left( {1-\nu } \right)}{1-\nu }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}\cdot n^{4}-\left( {\frac{4\cdot \left( {1+\delta_{m}^{2}} \right)-8\cdot \nu \cdot \delta_{m}^{2}}{\left( {1-\nu } \right)\cdot \delta_{m} }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}\cdot n^{4}-2\cdot n^{6}+} \\ {\left. {4\cdot \left( {1-\nu^{2}\cdot \delta_{m}^{2}} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{4}+\left( {\frac{2\cdot \left( {1+\delta_{m}^{2}} \right)-4\cdot \nu \cdot \delta_{m}^{2}}{1-\nu }} \right)\cdot \left( {\frac{\lambda_{m} \cdot R}{L}} \right)^{2}\cdot n^{2}+n^{4}} \right\} } \\ \end{array} } \] \[ \delta_{m} =1-\frac{2}{\lambda_{m} }\cdot \left( {\frac{sh\left( {\lambda _{m} } \right)\cdot ch\left( {\lambda_{m} } \right)-\lambda_{m} \cdot sh\left( {\lambda_{m} } \right)\cdot \sin \left( {\lambda_{m} } \right)-sh\left( {\lambda_{m} } \right)\cdot \cos \left( {\lambda_{m} } \right)-ch\left( {\lambda_{m} } \right)\cdot \sin \left( {\lambda_{m} } \right)+\sin \left( {\lambda_{m} } \right)\cdot \cos \left( {\lambda_{m} } \right)}{\left( {sh\left( {\lambda_{m} } \right)-\sin \left( {\lambda_{m} } \right)} \right)^{2}}} \right) \]
Собственные числа m-той балочной функции определяются из уравнения:
\[ ch\left( {\lambda_{m} } \right)\cdot \cos \left( {\lambda_{m} } \right)=1 \]
m= 2, 3, 4 - число узловых линий в окружном направлении с учетом линий по торцевым опорным контурам,
n = 0, 1, 2, ... - число пар узловых линий в меридиональном направлении при расположении каждой пары на одном диаметре.
Расхождения с теорией для начальных собственных частот связаны с тем, что частоты и формы собственных колебаний программа определяла для расчетной модели, имеющей все степени свободы узловых перемещений, т.е. учитывались и тангенциальные силы инерции. Эти силы особенно заметны на формах собственных колебаний, имеющих малое число полуволн m в окружном направлении.
Точное решение из источника построено без учета тангенциальных сил инерции. Но на странице 440 этого справочника приведена формула для оценки погрешности, которая вносится указанным предположением. Она дает величину поправки к квадрату собственной частоты:
k=1/(1+z).
Для первых форм, когда m=2 вычисления дали значение z=0,042. Следовательно, можно ожидать 2% поправки к теоретическому значению.
